Эддоус М., Стэнсфилд Р. Методы принятия решений

Подождите немного. Документ загружается.

Гл.

8. Линейная

регрессия

ПЪ

Остотки, .

млн. ф. ст. *" "

60 -

40 -

20 -

-20

-40

-*0

-80-J

i6o

200

0 о

Эбо

о 400 50О~

О о

Продажи

в мес,

млн. ф. ст.

Рис.

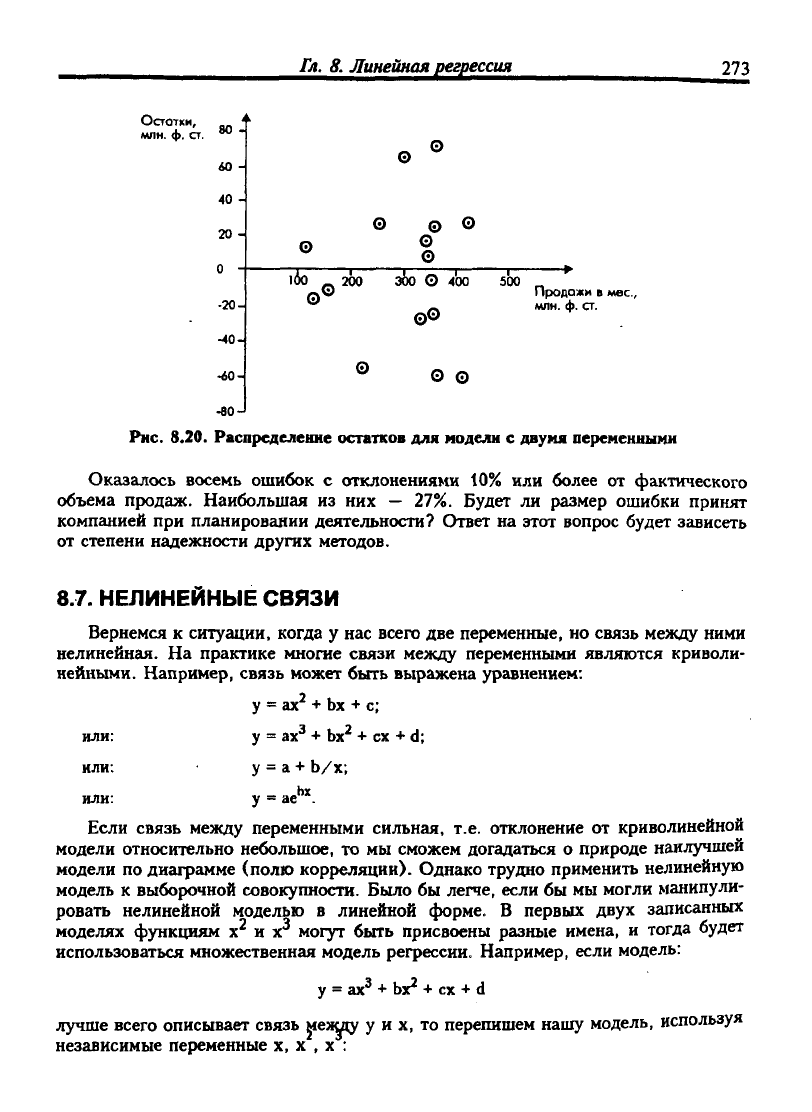
8.20. Распределение остатков для модели с двумя переменными

Оказалось восемь ошибок с отклонениями 10% или более от фактического

объема продаж. Наибольшая из них — 27%. Будет ли размер ошибки принят

компанией при планировании деятельности? Ответ на этот вопрос будет зависеть

от степени надежности других методов.

8.7.

НЕЛИНЕЙНЫЕ

СВЯЗИ

Вернемся к ситуации, когда у нас всего две переменные, но связь между ними

нелинейная. На практике многие связи между переменными являются криволи-

нейными. Например, связь может быть выражена уравнением:

у = ах + Ьх

с;

или: у = ах^ +

Ьх^

+ сх

или: у = а

Ь/х;

или: у

ае .

Если связь между переменными сильная, т.е. отклонение от криволинейной

модели относительно небольшое, то мы сможем догадаться о природе наилучшей

модели по диаграмме (полю корреляции). Однако трудно применить нелинейную

модель к выборочной совокупности. Было бы легче, если бы мы могли манипули-

ровать нелинейной моделью в линейной форме. В первых двух записанных

моделях функциям х и х могут быть присвоены разные имена, и тогда будет

использоваться множественная модель регрессии. Например, если модель:

у = ах^ +

Ьх^

+ сх

лучше всего описывает связь между у и х, то перепишем нашу модель, используя

независимые переменные х, х , х :

274

4.2.

Анализ данных

как

составная часть принятия решений

у =

ЬХ +

сх + d,

где Z =

и X =

Эти переменные рассматриваются как обыкновенные независимые перемен-

ные, даже если мы знаем, что Z, X и х не могут быть кезависимы друг от друга.

Лучшая модель выбирается так же, как и в предыдущем разделе.

Третья и четвертая модели рассматриваются по-другому. Тут

мы

уже встречаемся

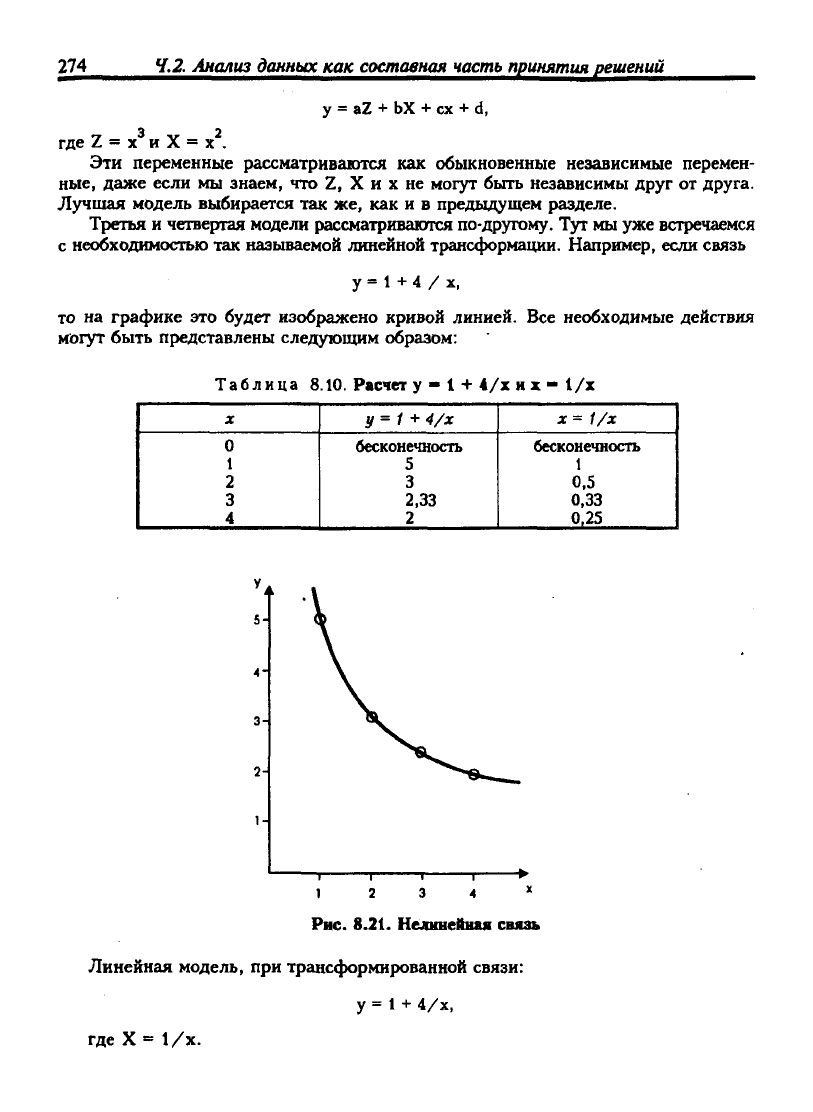
с необходимостью так называемой линейной трансформации. Например, если связь

у =

+ 4 / X,

то на графике это будет изображено кривой линией. Все необходимые действия

могут быть представлены следующим образом:

Таблица 8.10. Расчет у - 1 + 4/х и х - 1/х

у=1 •^4/х

бесконечность

2,33

х= 1/х

бесконечность

0,5

0,33

0,25

12 3 4"

Рис. 8.21. Нелинейная связь

Линейная модель, при трансформированной связи:

у =

+ 4/х,

где X = 1/х.

Гл.

8. Линейная

регрессия

275

^ Тронсформировоно • линию

I-

1 1 1 1 *

0,25 0,50 0,75 1,0 ХЧ/х

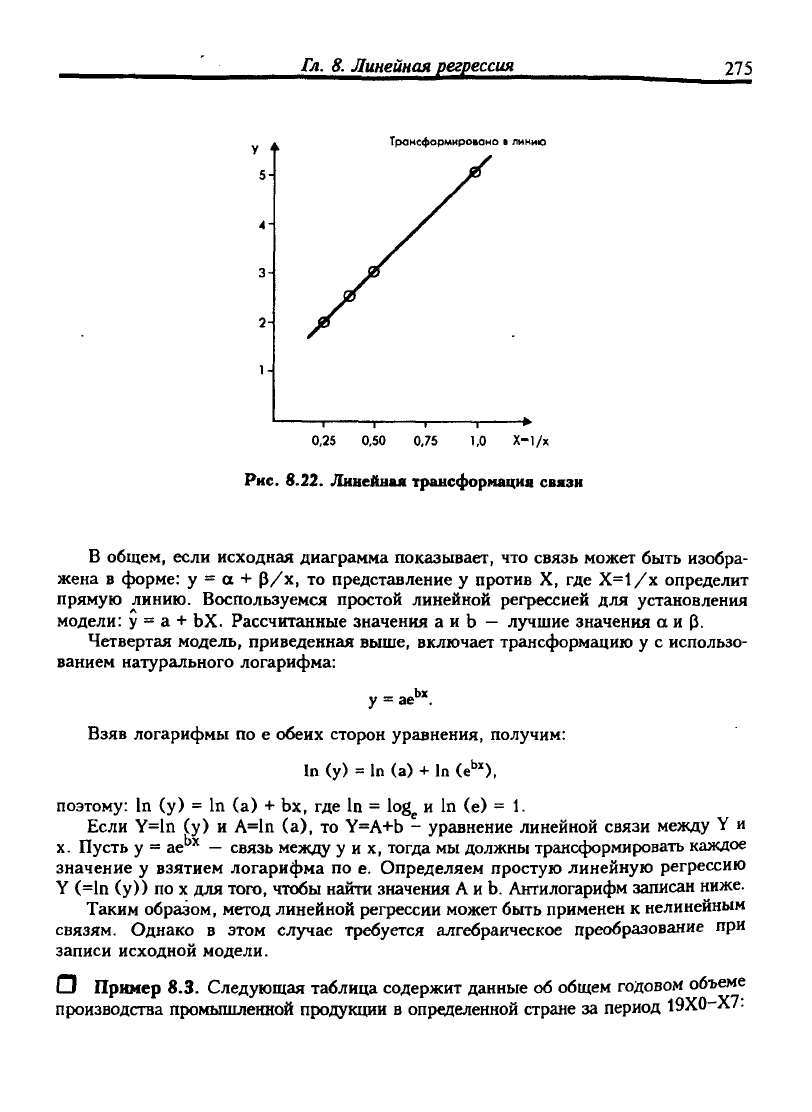
Рис.

8.22. Линейная трансформация связи

В общем, если исходная диаграмма показывает, что связь может быть изобра-

жена в форме: у = а + р/х, то представление у против X, где Х=1/х определит

прямую линию. Воспользуемся простой линейной рефессией для установления

модели: у = а + ЬХ. Рассчитанные значения а и Ь

—

л)гчшие значения а и р.

Четвертая модель, приведенная выше, включает трансформацию у с использо-

ванием натурального логарифма:

у = ае .

Взяв логарифмы по е обеих сторон уравнения, получим:

In (у) = In (а) + In

(е"""),

поэтому: In (у) = In (а) + Ьх, где In = log^ и In (е) = 1.

Если Y=ln (у) и А=1п (а), то Y=A-^b - уравнение линейной связи между Y и

X. Пусть у = ае

—

связь между у и х, тогда мы должны трансформировать каждое

значение у взятием логарифма по е. Определяем простую линейную регрессию

У (=1п (у)) по

для того, чтобы найти значения А и Ь. Антилогарифм записан ниже.

Таким образом, метод линейной регрессии может быть применен к нелинейным

связям. Однако в этом сдз^чае требуется алгебраическое преобразование при

записи исходной модели.

а Пример 8.3. Следующая таблица содержит данные об общем годовом объеме

производства промышленной продукции в определенной стране за период 19Х0-л/-

276 4.2. Анализ

данных

как

составная часть принятия решений

Таблица 8.11. Годовой объем продукции 19X0-Х7

Год

19X0

19X1

19X2

19X3

19X4

19X5

19X6

19X7

Годоаая

продукция.

тыс. т

740

804

879

961

1042

1137

1242

1357

Требуется:

Нарисовать диаграмму, прокомментировать ее.

Нарисовать новую диаграмму за следующий год.

Предположим, что связь между общей годовой продукцией и временем

может быть описана как:

у =

аЬ",

где у

—

общий объем годовой продукции их

—

число лет с 19X0.

Используйте выборочную совокупность для оценки а и

Ь.

Объяснить получение Ь.

Используйте модель, описанную в п.З, для прогнозирования общего объема

продукции. Прокомментируйте ващ прогноз.

Решение

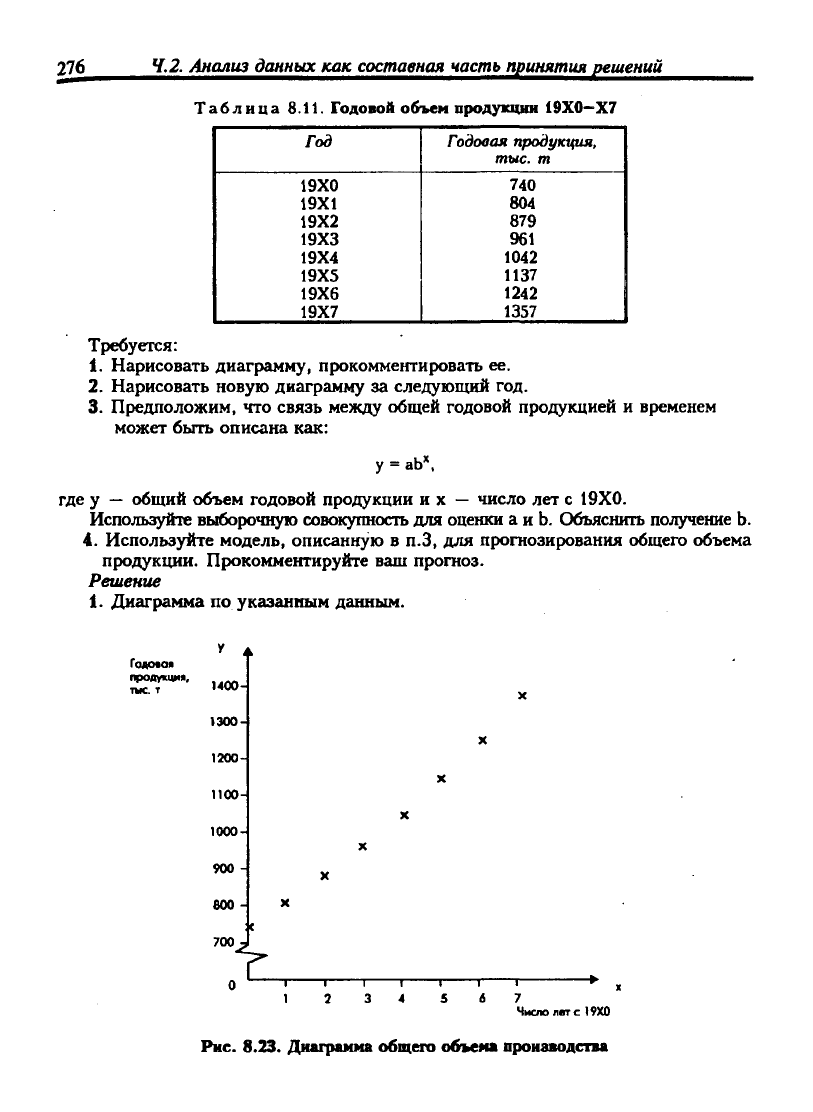
Диаграмма по указанным данным.

Годоааа

продупип,

тыс т

1400-

1300-

1200-

1100-

1000-

900 -

800-

700

г.

-1—1—1 ,

5 4 7

Число лат с 19X0

Рис. 8.23. Диаграмма общего объема пронзводспа

Тл.

Линейная регрессия

277

Рисунок показывает, что между у и х существует некая связь, но она может

быть криволинейной.

Трансформируем для начала значения объема производства в логарифми-

ческой форме.

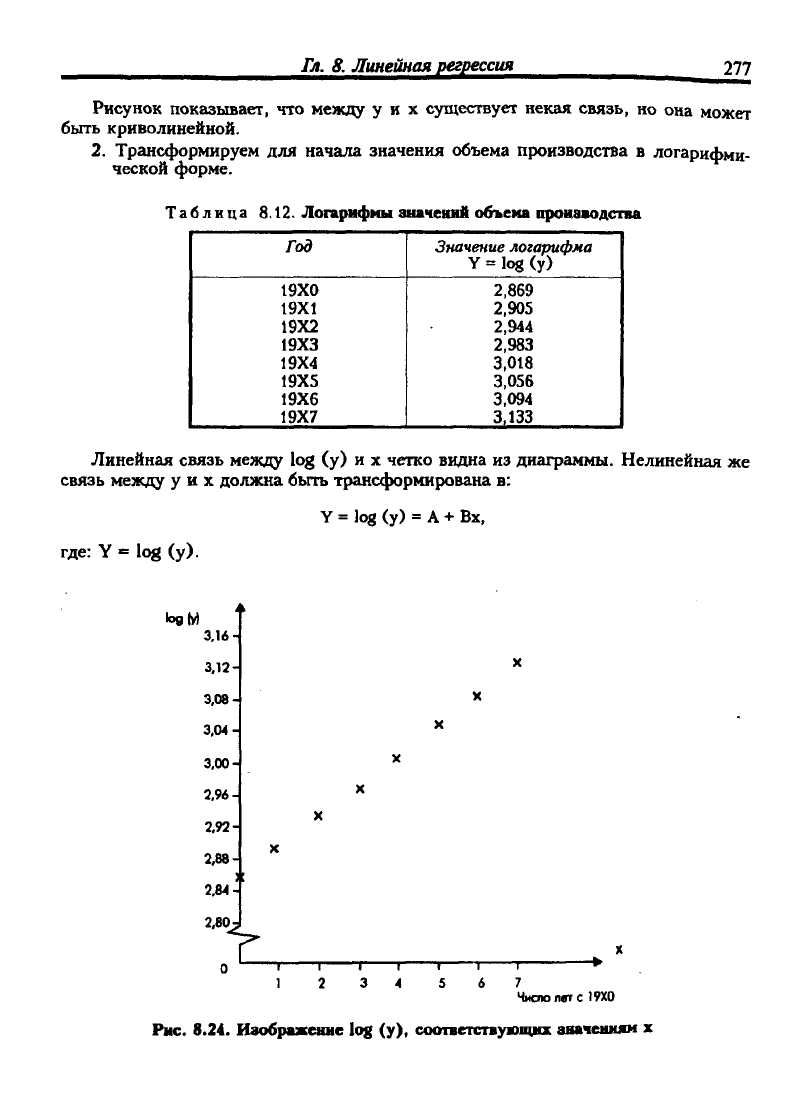
Таблица 8.12. Логарифмы значений объема производства

Год

19X0

19X1

19X2

19X3

19X4

19X5

19X6

19X7

Значение логарифма

Y = log (у)

2,869

2,905

2,944

2,983

3,018

3,056

3,094

3,133

Линейная связь между log (у) и х четко видна из диаграммы. Нелинейная же

связь между у и х должна быть трансформирована в:

где:

Y = log (у).

Y = log (у) = А + Вх,

logM

3,16

3,12

3,Св-

3.04

3,00

2,96

2,92

2,88

7М

2,80

1 2 3 4 5 6 7

Число лет с 19X0

Рнс. 8.24. Изображение log (у), соответствуюи(нх зиаченшш х

278

4.2. Анализ данных как составная

часть

принятия решений

Предполагаемая модель:

у = аЬ*.

Пролагорифмируем обе части:

log (у) = log (ab*) - log (а) + log (b").

Отсюда:

log (у) = log (a) + xlog (b).

Пусть A = log (a) и В = log (b). Тогда ожидаемая линейная модель:

Y = log (у) =

+ Вх.

Для оценки А и В используем технику простой линейной регрессии:

Таблица 8.13. Расчеты для модели регрессии

Год

19X0

19X1

19X2

19X3 .

19X4

19X5

19X6

19X7

Всего

Log (годовая продукция)

Y = log (у)

2,869

2,905

2,944

2.983

3,018

3,056

3,094

3,133

24,002

Число

лет

с 19X0

х2

140

xlog (у)

2,905

5,888

8,949

12,072

15,280

18,564

21.931.

85,589

Для выявления наилучшей модели применяется метод наименьших квадратов

в выборочной совокупности:

^ n^(xlog(y))-2;xXlog(y)

3,8-85.589-28-24002 ^0^3767.

8-140 - (28Г

Коэффициент А находится как:

nA =

2;iog(y)-B2^x.

т.е.

8А = 24,002 - 0,03767

•

28,

А = 2,8684.

Гл.

Линейная регрессия

Поэтому линейная модель:

log (у) = 2,8684 + 0,037б7х,

так как А = log (а), то а = 10^ = 738,6. Так как В = log (Ь), то Ь = 10^ =

Связь между общим объемом годовой продукции и числом лет с 19X0

быть описана:

у = 739•(1,091)^

Интерпретация Ь: если мы перепишем эту модель таким образом:

у = 739 (1+9,1/100)", то природа связи станет более очевидна. Годовая про,

739 (тыс. т) в 19X0 году при х=0. Затем мы видим, что продукция растет г

в год. Ь

—

отношение объема производства в текущем году к объему произв

в предыдущем году. Прогноз будущего объема прюдукции:

19X8:

= 8, у = 739 (1,091)^ = 1483 тыс, т;

19X9:

= 9, у = 748 (1,091)^

1618 тыс. т.

Нужно быть предельно внимательными, когда мы расширяем рамки м

построенной по выборочной совокупности. Предположим, что условия с 15

19X7 годы остаются неизменными. Это предложение может быть оправд

для прогноза на 19X8 год, но по мере того как мы будем двигаться далее, п

станет все менее надежен.

8.8. РАНГОВЫЙ КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ СПИРМЕНА г

В предыдущих разделах предполагалось, что данные включают в себя ка

измерения. Если же возможны какие-либо процедуры, связанные с пострс

последовательности, то действия без параметров неуместны. Типичным при

являются маркетинговые исследования, например, исследование вкуса лищи

нам понадобится испробовать четыре вида супа, то мы можем располож!

в последовательности в порядке предпочтения от

до 4, но мы не сможем у

точный принцип предпочтения. Такой вид данных называется порядк

Данные, которыми мы пользовались до настоящего времени, называются i

вальными.

Положим, двух людей попросили попробовать четыре вида супа. Вер'

что будет иметь место два вида вариаций принципов предпочтения. Две по'

вательности составляют две порядковые переменные. Мы можем сравни'

последовательности по степени согласованности, используя ранговый

KOS

циент корреляции Спирмена.

Коэффициент Спирмена г, не является параметрическим критерием в

чип от коэффициента Пирсона:

6ld^

n (n^ - 1)

280

4.2. Анализ данных как составная

часть

принятия решений

где d — разница между значениями рангов для каждой единицы. Так же как и

коэффициент Пиркюна, значение г^ изменяется от -1 до +1. Значимость коэффици-

ента Спирмена может бьггь проверена таким же образом, что и значение коэффи-

циента Пирсона.

• Пример 8.4. Два человека дегустируют 10 супов. Нам нужно узнать, какой

уровень согласованности достигнут между этими двумя дегустаторами.

Таблица 8.14. Определение уровня согласованности

между двумя дегустаторами

Дегуапатор^

Первый

Второй

Разница

(d)

-2

-1

-3

Всего

Отсюда:

6-26

10-99'

1 - 0,158 »

0,842

Для того чтобы оценить достоверность этого результата, укажем гипотезы,

которыми мы руководствуемся.

HQ:

между двумя дегустаторами либо нет связи, либо они просто не согласо-

ваны друг с другом, т. е. р S 0.

Hf. существует согласованность (положительная связь), т.е. Ps>0.

Это односторонний критерий. Двусторонний критерий мы бы использовали,

если бы нас интересовала либо положительная, либо отрицательная связь.

Значение критерия для п ^ 10 (приближенно) имеет вид:

(г»

- 0)

0,842

Из стандартных таблиц:

(п - 1) VJ

Zo,os=

1.645.

•

2,53.

Полученное значение критерия больше, чем

1,645.

Результат достоверен на

5%-ном

уровне. Отвергаем

и становится очевидной положительная связь между

двумя дегустаторами. Нормальному приближение распределения верно только для

п i 10. Для п < 10 существуют специальные таблицы.

Гл.

8. Линейная

регрессия

281

РЕЗЮМЕ

Построение линейной регрессии

—

это не что иное, как построение модели. Нам

нужно объяснить изменяемость зависимой переменной в результате изменения

независимой переменной.

Построение модели всегда начинается с выбора факторов, которые, вероятно,

могут повлиять на зависимую переменную. Необходимо выбрать основные из них.

В простой линейной регрессии (парной) имеется только одна независимая пере-

менная. Модель выражается как:

у = о

+ рх

Е,

где

- остаток, часть у, которая не объясняется моделью, рассчитываемой

юбычно

по выборочной совокупности при помощи метода наименьших квадратов. Для

прямой линии показатель наклона рассчитывается по формуле:

а пересечение с осью OY:

^_ 1У Ь^х

~ п п •

Теснота линейной связи измеряется коэффициентом корреляции Пирсона г:

п^ху- ^х^у

'"V(n2:x2-(Xx)^(n5:y^-{2]y)')

Чем ближе г к -1 или к +1, тем точнее линейная модель описывает связь

между

и у. Коэффициент детерминации, г^, измеряет долю вариации у, объяс-

нимой X.

Кроме того, предполагается, что остатки нормально распределены с нулевым

средним значением и стандартным отклонением о^, которое постоянно для всех

значений х. Доверительные интервалы могут быть установлены для параметров

р,

а и Р с использованием выборочных оценок г, а и Ь. Для оценки достоверности

используют гипотезы о значениях параметров. Для всех критериев нулевые

гипотезы являются предположением о том, что в генеральной совокупности между

переменными в генеральной совокупности не существует линейной связи. Значе-

ние критерия для р будет следующим:

при (п-2) степенях свободы;

282

4.2. Анализ данных как составная

часть

принятия решений

дяяр:

t =

b-0

a./VX(x-xy

^\i

при (п-2) степенях свободы.

Для данного х, скажем хо, рассчитывается доверительный интервал для

среднего значения у и для индивидуальных значений у, близких к среднему

значению. Ширина таких интервалов изменяется, и они могут быть изо6р>ажены с

помощью кривых линий с каждой стороны линии регрессии.

Множественная регрессия имеет более чем одну независимую переменную в

модели.-Обычно в этом случае все расчеты производятся с помощью компьютера.

Для проверки достоверности связи также используют гипотезы. Если мы исследуем

большое количество независимых переменных, применяется быстрый метод исключе-

ния недостоверных и не имеющих силу моделей и построения лучших моделей.

Нелинейные модели алгебраически могут быть превращены в линейные.

Коэффициент ранговой корреляции Спирмена рассчитывается аналогично, как

и коэффициент Пирсона, когда нам важно прежде всего упорядочивание данных,

нежели прямое измерение.

УПРАЖНЕНИЯ

Упражиенне 8.1 .

Торговцу нужно выяснить, как изменяется количество пучков салата, продава-

емого ежедневно в розницу.

Требуется определить факторы, которые могут повлиять на количество.

Имеются следующие сведения о количестве и цене:

Количестоо, тыс./день

Цена, ф. ст. за единицу

Требуется:

а) изобразить данные на графике, вычислить коэффициент корреляции г,

найти достоверность на уровне 1%;

б) построить модель линейной регрессии и объяснить значения коэффшщентов;

в) если бы цена салата была равна 45 ф. ст. за каждый пучок, то сколько было

бы продано? Прокомментируйте ваши предположения.

Упражнение 8.2

Провели исследование, сколько сберетает население и сколько оно зарабатывает за год.

Были получены следующие данные для случайно отобранных 9 чел.:

Доход, тыс. ф. ст.

Сбережения, ф. ст.

2000

200

500

2500

1800

1500

1600