Эддоус М., Стэнсфилд Р. Методы принятия решений

Подождите немного. Документ загружается.

Гл.

Временные ряды

прогнозирование

303

Построим по этим данным точечную диаграмму:

Объем продаж этого продукта так же, как и в предыдущем примере, подвер-

жен сезонным колебаниям, и значения его в зимний период выше, чем в летний.

Однако размах вариации фактических значений относительно линии тренда посто-

янно возрастает. К таким данным следует применять модель с мультипликативной

компонентой:

Фактическое значение = Трендовое значение х Сезонная вариация х Ошибка

т. е.

А = Т X S

Е.

В нашем примере есть все основания предположить существование линейного

тренда, но чтобы полностью в этом убедиться, проведем процедуру сглаживания

временного ряда.

9.4.1.

Расчет

значений

сезонной компоненты

В сущности эта процедура ничем не отличается от той, которая применялась для

аддитивной модели. Так же вычисляются центрированные скользящие средние

для трендовых значений, однако оценки сезонной компоненты представляют собой

коэффициенты, полученные по формуле А/Т = S х Е. Результаты расчетов

приведены в табл. 9.7.

Таблица 9.7. Р»счет значений ссаоивой коипоневт для CD pic

Дата

Январь-март 19X6

Апрель-июнь

Июль-сентябрь

Октябрь-декабрь

Январь-март 19X7

Апрель-июнь

Июль-сентябрь

Номер

каартаяа

Объем

продаж,

тыс.

шт.

Скользящая

средняя

за

четыре

каартаяа

70,25

70,75

73.50

74,75

Центрирован-

ная

скользящая

средняя

69,13

70,25

70.50

72,13

74,13

Коэффициент

сезонности

А/Т

= 5

0,940

1,011

1,121

0,915

0,904

Ч.

Анализ данных

как

составная часть принятия решений

Октябрь-декабрь

Январь-март

19X8

Апрель-июнь

Июль-сентябрь

Октябрь-декабрь

Яиват-март

19X9

Значения сезон

ных коэф<

)Ициентов

75,50

76,75

80,50

получены на

75,13

76,13

77,38

79,25

•"

Продолжение

1,092

1,103

0,892

0,909

основе квартальных оценок

по аналогии с алгоритмом, который применялся для аддитивной модели. Так как

значения сезонной компоненты — это доли, а число сезонов равно четырем,

необходимо, чтобы их сумма была равна четырем, а не нулю, как в предыдз^ем

случае. (Если бы в исходных данных предполагалось семь сезонов в течение

недели по одному дню каждый, то общая сумма значений сезонной компоненты

должна была бы равняться семи). Если эта сумма не равна четырем, производится

корректировка значений сезонной компоненты точно таким же образом, как это

уже делалось ранее. В таблице оценки, рассчитанные в последнем столбце пред-

шествующей табл. 9.8, расположены под соответствующим номером квартала.

Таблица 9.8. Расчет

яижчкшА

сезонной коиповевш дм CD pic

Итого

Среднее

значение

Оценка

сезонной

южшоненш

Скорректи-

рованная

сезонная

компонента*

Год

19X6

19X7

19X8

1,121

1,103

2,224

2,224 + 2

1,112

1,116

Номер квартала

0,915

0,892

1,807

1,807+2

0,903

0,907

0,940

0,904

0,909

2,753

2,753+2

0,918

0,922

1,011

1.092

2,103

2,103 +2

1,051

1,055

Сумма = 3,984

Сумма = 0

* Скорректированная оценка сезонной компоненты получена

результате умножения

соответствующей доли на (4/3,984).

Гл.

Временные ряды

прогнозирование

305

Как показывают оценки, в результате сезонных воздействий объемы продаж в

январе

—марте

увеличиваются на 11,6% соответствующего значения тренда

(1,116).

Аналогично сезонные воздействия в октябре-декабре приводят к увеличе-

нию объема продаж на 5,5% от соответствующего значения тренда. В двух других

кварталах сезонные воздействия состоят в снижении объемов продаж, которое

составляет 90,7 и 92,2% от соответствующих трендовых значений.

9.4.2. Десезонализация данных и расчет уравнения тренда

После того как оценки сезонной компоненты определены, можем приступить к

процедуре десезонализации данных по формуле А /S = Т х Е. Результаты

расчетов этих оценок значений тренда приведены в табл. 9.9.

Таблица 9.9. Расчет уравнения тренда для компанин CD pic

Дата

Январь-март 19X6

Апрель-июнь

Июль-сентябрь

Октябрь-декабрь

Январь-март 19X7

Апрель-июнь

Июль-сентябрь

Октябрь-декабрь

Январь-март 19X8

Апрель-июнь

Июль-сентябрь

Октябрь-декабрь

51нварь-март 19X9

Номер

квартала

Обьем

продаж,

тыс.

шт.

Коэффициент

сезонности

1,116

0,907

0,922

1,055

1,116

0,907

0,922

1,055

1,116

0,907

0.922

1,055

1,116

11есезонализированны1

объем продаж,

тыс. шт.

A/T

= Sx Е

62,7

72,8

70.6

67.3

70,8

72,8

72,7

77,7

75,2

76.1

78,2

82.4

84,2

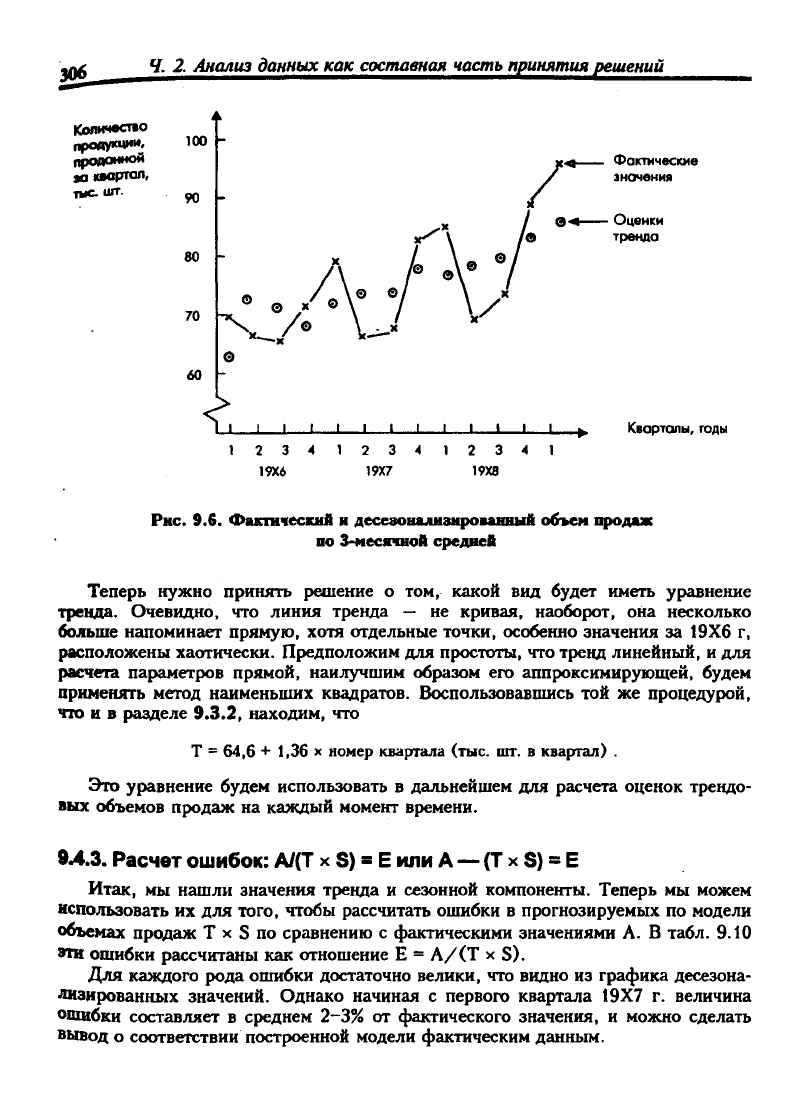
Полученные трендовые значения наносятся на исходную точечную диаграмму.

Точки, образующие представленный на графике тренд, достаточно сильно

разбросаны. (Збъемы продаж в данном случае не образуют такой строгой последо-

вательности, как в предыдущем примере с компанией Lewplaa pic. Скорее всего,

пример с CD pic более близок к реальной действительности.

Ч. 2. Анализ данных как составная

часть

принятия решений

Колинвсяо

проаухчии, 100

проломной

за квартал,

тис.

шт. 90

Фактические

эночения

- Оценки

тренда

I I I I I I 1 I I ' I

2 3 4

19X6

12 3 4

19X7

12 3 4

19X8

Кворталы,годы

Рис. 9.в. Фактический и десеаонализированвый объем продаж

по 3-месячной средней

Теперь нужно принять решение о том, какой вид будет иметь уравнение

тренда. Очевидно, что линия тренда — не кривая, наоборот, она несколько

больше напоминает прямую, хотя отдельные точки, особенно значения за 19X6 г,

расположены хаотически. Предположим для простоты, что тренд линейный, и для

расчета параметров прямой, наилучшим образом его аппроксимирующей, будем

применять метод наименьших квадратов. Воспользовавшись той же процедурой,

что и в разделе 9.3.2, находим, что

Т = 64,6 + 1,36

номер квартала (тыс. шт. в квартал) .

Это уравнение будем использовать в дальнейшем для расчета оценок трендо-

вых объемов продаж на каждый момент времени.

9Д.З.

Расчет

ошибок:

А/(Т

S) = Е

или А

—

(Т х

S) = Е

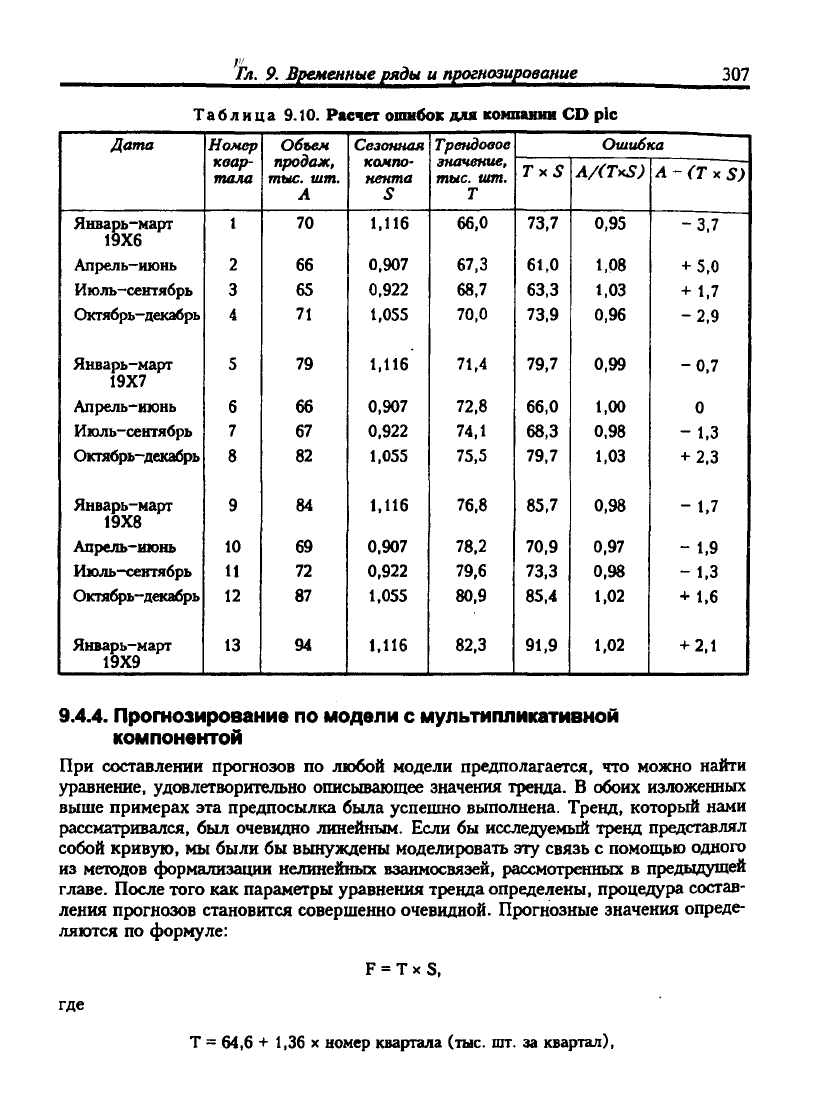
Итак, мы нашли значения тренда и сезонной компоненты. Теперь мы можем

использовать их для того, чтобы рассчитать ошибки в прогнозируемых по модели

объемах продаж Т х S по сравнению с фактическими значениями А. В табл. 9.10

эти ошибки рассчитаны как отношение Е = А/(Т х S).

Для каждого рода ошибки достаточно велики, что видно из графика десезона-

лизированных значений. Однако начиная с первого квартала 19X7 г. величина

ошибки составляет в среднем 2-3% от фактического значения, и можно сделать

вывод о соответствии построенной модели фактическим данным.

Гл.

Временные ряды

прогнозирование

307

Дата

Январь-март

19X6

Апрель-июнь

Июль-сентябрь

Октябрь-декабрь

Январь-март

19X7

Апрель-июнь

Июль-сентябрь

Октябрь-декабрь

Январь-март

19X8

Апрель-июнь

Июль-сентябрь

Октябрь-декабрь

Январь-март

19X9

аблица 9.10. Расчет ошибок для компавии CD pic

Номер

квар-

тала

Объем

продаж,

тыс.

шт.

Сезонная

компо-

нента

1.116

0,907

0,922

1,055

1,116

0,907

0,922

1,055

1,116

0,907

0,922

1,055

1,116

Трендовое

значение,

тыс.

шт.

66,0

67,3

68,7

70,0

71,4

72,8

74,1

75,5

76,8

78,2

79,6

80,9

82,3

TxS

73,7

61,0

63,3

73,9

79,7

66,0

68,3

79,7

85,7

70,9

73.3

85,4

91,9

Ошибка

A/(TxS)

0,95

1.08

1.03

0.96

0.99

1,00

0,98

1.03

0,98

0,97

0,98

1,02

1.02

А-(TxS)

-3,7

+ 5,0

+ 1,7

-2,9

-0,7

-1.3

+ 2,3

- 1.7

- 1.9

-1.3

+ 1,6

+ 2,1

9.4.4. Прогаозирование по модели с мультипликативной

компонентой

При составлении прогнозов по любой модели предполагается, что можно найти

уравнение, удовлетворительно описывающее значения тренда. В обоих изложенных

выше примерах эта предпосылка была успешно выполнена. Тренд, который нами

рассматривался, был очевидно линейным. Если бы исследуемьй тренд преяставлял

собой кривую, мы были бы вынуждены моделировать эту связь с помощью одного

из методов формализации нелинейных взаимосвязей, рассмотренных в предыдущей

главе. После того как параметры уравнения тренда определены, процедура состав-

ления прогнозов становится совершенно очевидной. Прогнозные значения опреде-

ляются по формуле:

где

Т = 64,6 + 1,36

номер квартала (тыс. шт. за квартал),

чпЯ Ч. 2. Анализ данных как составная часть принятия решений

а сезонные компоненты составляют 1,116 в первом квартале, 1,097 — во втором,

О 922 — в третьем и 1,055 в четвертом квартале. Ближайший следующий квартал

J. это второй квартал 19X9 г., охватывающий период с апреля по июнь и

имеющий во временном ряду порядковый номер 14. Прогноз объема продаж в этом

квартале составляет:

F = Т

S = (64,6 + 1,36

14)

0,907 = 83,64 х 0,907 = 75,9 (тыс. шт. за квартал).

С учетом величины ошибки прогноза мы можем сделать вывод, что данная

оценка будет отклоняться от фактического значения не более чем на 2-3%.

Аналогично, прогноз на октябрь-декабрь 19X9 г., рассчитывается для квартала с

порядковым номером 16 с использованием значения сезонной компоненты для IV

квартала года:

F = Т

S = (64,6 + 1,36

16)

1,055 = 83,36 х 1,055 = 91,1 (тыс. шт. за квартал) .

Разумно предположить, что величина ошибки данного прогноза будет несколь-

ко выше, чем предыдущего, поскольку этот прогноз рассчитай на более длитель-

ную перспективу.

РЕЗЮМЕ

Под временным рядом понимается любое множество данных, относящихся к

определенным моментам времени. Это могут быть, скажем, годы, кварталы,

месяцы или недели. В моделях временного ряда ретроспективная тенденция

используется для прогнози])ования поведения переменной в будущем. Краткосроч-

ные прогнозы являются более точными, чем долгосрочные. Если прогноз состав-

лялся на более длительный период времени при условии, что существующая

тенденция сохранится в будущем, то тем больше величина ошибки.

Для моделирования временных рядов используются два типа моделей —

аддитивная и мультипликативная. В обоих случаях предполагается, что значение

переменной включает в себя ряд компонент. Временной ряд может состоять из

собственно тренда — общей тенденции изменения значений переменной; сезонной

вариации ~ краткосрочных периодических колебаний значений переменной; цик-

лической вариации — долгосрочных периодических колебаний значений перемен-

ной; ошибки или остатка. В данном учебном пособии не рассматривались массивы

данных за длительные промежутки времени, содержащие циклическую вариацию.

Рассмотренные нами модели имеют следующий вид:

Аддитивная А = Т + S

+•

Е ,

Мультипликативная А = Т х S х Е .

В обоих видах моделей для десезоиализации данных применяется метод

скользящего среднего. Затем десезонализировакные данные используются при

построении модели тренда. По этой модели составляют прогнозы будущих значе-

ний тренда. В случае линейной модели для нахождения параметров прямой,

наилучшим образом аппроксимирующей фактические значения, используется

Гл.

Временные ряды

прогнозирование

309

метод наименьших квадратов. Процесс построения нелинейных моделей гораздо

более сложен.

В отличие от линейных регрессионных моделей для оценки обоснованности

или точности прогнозных моделей статистические методы, как правило, не исполь-

зуются. Наилучшую среди нескольких моделей выбирает специалист, составляю-

щий прогноз. Чтобы определить, насколько точно рассматриваемая модель апп-

роксимирует прошлые данные, применяются два показателя:

Среднее абсолютное отклонение (MAD) =

1|Е,1

Среднеквадратическая ошибка (MSE)

••

I(Et)^

УПРАЖНЕНИЯ

Упражнение 9.1

За последние И кварталов товарооборот компании "Amada pic", скорректирован-

ный на инфляцию, составил:

Год

Коарт^л

Товарообо-

рот

2 3

43 43

Требуется:

В предположении существования линейного тренда построить модель с аддитив-

ной компонентой.

Сделать прогноз на ближайшие три квартала. Прокомментировать вопрос о

вероятной точности ваших прогнозов.

Упражнение 9.2

Спрос на стулья, которые продает компания "Peace Retailers", составил:

Год

Квартал

Спрос

157

137

156

2 3

151 153

141

154

2 3

152 154

142

Требуется:

Построить соответствующую модель с аддитивной компонентой.

Дать прогноз на первые два квартала четвертого года.

310

Ч. 2. Анализ данных как составная часть принятия решений

Упражнение 9.3

Ниже приведены квартальные объемы вьшуска продукции компании "Coboumes

pic":

Год

Квартал

Объем

выпуска

2 3

89 79

100

Требуется:

Проанализировать значения квартальных объемов вьшуска на основе модели с

аддитивной компонентой.

Прокомментировать поведение тренда.

Упражнение 9.4

Положение дел в компании "Doble-Flood" достаточно тяжелое. Ниже приводятся

данные о прибыли компании за последние 10 кварталов (скорректированные на

инфляцию).

Год

Квйргпал

Прибыль

146

106

123

2 3

74 80

1 2

56 35

Требуется:

Построить модель времевного ряда с мультипликативной компонентой.

Дать прогноз на 2 следующих квартала года 3.

Упражнение 9.S

Объемы выпуска компании "Banham and Barsey" возрастают из года в год. Ниже

приведены значения этого показателя.

Год

Квартал

Объем

выпуска

400

715

600

585

2 3

560 975

800

765

720

1235

Требуется:

Построить соответствующую модель временного ряда с мультипликативной

компонентой.

Дать прогноз на два следующие квартала.

Упражнение 9.6

Используя данные для "Peace Retailers" из упражнения 9.2.

Гл.

Временные ряды

прогнозирование

311

Требуется:

Рассчитать ошибку, среднее абсолютное отклонение (MAD) и среднеквадрати-

ческую ошибку (MSE) для модели с аддитивной компонентой, построенной в

упражнении 9.2.

Используя простую экспоненциальную модель скользящего среднего при Fo =

150 и а - 0,2, вычислить прогнозные значения, ошибку и соответствующие

MAD и MSE.

Сравнить результаты, полученные в п.п. 1 и 2, и сделать вывод о том, какая из

моделей лучше.

Упражнение 9.7

В июне 1990 г. директор-распорядитель крупного мебельного магазина "Cushair

Designs" пригласил консультанта по менеджменту с целью разработать простой и

практичный метод прогнозирования уровней квартальных объемов продаж магази-

на на шесть месяцев вперед. В процессе решения этой задачи консультант пришел

к вьшоду, что метод прогнозирования, отвечающий этой цели, в первую очередь

предполагает десезонализацию валового объема продаж за последние 30 месяцев.

Затем полученные значения временного ряда можно нанести на график, построить

прямую, наилучшим образом их аппроксимирующую, и экстраполировать полу-

ченную тенденцию на ближайшие два квартала. Применение соответствующего

индекса сезонности к этим значениям позволит получить оценки объемов продаж

на два следующих квартала.

Значения валового объема продаж Cushair Designs

Период

продаж

Январь-март 1988

Апрель-июнь 1988

Июль-сентябрь 1988

Октябрь-декабрь 1988

Январь-март 1989

Апрель-июнь 1989

Июль-сентябрь 1989

Октябрь-декабрь 1989

Январь-март 1990

Апрель-июнь 1990

Обг>ем розничной

продажи,

тыс. ф. ст.

285

310

315

385

340

370

375

460

395

425

Консультант по менеджменту дал также некоторые рекомендации по поводу

того,

как можно избежать расчета индексов сезонности для универмага. Он счел

эту продедуру нецелесообразной, поскольку в его распоряжении было слиипсом

мало информации за прошлые периоды. Он решил использовать национальный

поквартальный индекс сезонности, значения которого публикуются в прессе.

Он предполагал, что ассортиментный набор мебельного магазина его клиента

Ч.

Анализ данных

как

составная часть принятия решений

ясзначигельно отличается от того ассортиментного набора, на основе которого

(^троится

национальный индекс.

Национальный поквартальный индекс

сезонности продаж для иебели

Январь-март

Апрель-июнь

Июль-сентябрь Октябрь-декабрь

Мультипли-

кативный индекс

98 96 112

сезонности

Требуется:

а) Нанести на график фактические значения квартальных объемов продаж и

объяснить, почему мультипликативная модель соответствует этим данным в

большей степени, чем аддитивная.

б) Найти значения десезоналиэированных данных и нанести их на график.

в) Используя метод наименьших квадратов, определить параметры уравнения

прямой, проходящей через десеэонализированные данные.

г) Рассчитать оценки валового объема продаж

третьем и четвертом кварталах

1990 г.

д) Определить вероятную точность полученных оценок.