Эддоус М., Стэнсфилд Р. Методы принятия решений

Подождите немного. Документ загружается.

Гл.

Статистический

вывод 2:

испытание

гипотез 153

Случай 1:

HQ:

= 2,0 см,

Н,:

ц»*

2,0

см.

Случай 2:

HQ:

= 2,0 см,

Hj:

м >

2,0 см.

£сли

результат относится к категории 3, то никакое решение не может быть

принято до тех пор, пока не будет получено больше данных,и испытание гипотезы

будет прюведено вновь. Однако следует отметить, что разграничение этих трех

категорий проводится на субъективной основе лицом, принимающим решение.

Какой бы результат ни был получен, мы никогда не можем определенно (на 100%)

доказать или опровергнуть нулевую гипотезу. Все, что мы можем сделать,— это

или признать то, что нулевая гипотеза почти наверняка верна, или, что правиль-

ность нулевой гипотезы маловероятна.

Следующий пример поможет прояснить, почему это так.

О Пример 6.1. Рассмотрим еще раз эксперимент с бросанием кости 102 раза.

Выпало 20 "шестерок". Очевидно ли то, что на выпадении "шестерок" сказалось

влияние какого-то неслучайного фактора?

Решение

Если кость без смещения, то число выпадения "шестерок" при 102 бросаниях

подчиняется биномиальному распределению.

Нулевая гипотеза предполагает, что число "шестерок" биномиально распределено

с р=1/6, то есть на выпадение "шестерок" не оказьшается какого-либо воздействия.

Альтернативная гипотеза предполагает, что на кость было оказано влияние для

более частого выпадения "шестерок"

—

число "шестерок" не подчиняется биноми-

альному распределению с р=1/6.

Вероятность достижения г "шестерок" из 102 бросаний, если на кость не

оказано влияние, находится следующим образом:

Р (г)

'"^С,

(1/6/

(5/6)'°^"^ г = 0. 1, 2, 3 102.

Поэтому вероятность наблюдаемого числа "шестерок" равна:

Р (г

20)

'"^Сзо

(1/6)^°

(5/6)'^

0,073

т. е. это событие маловероятно.

Вероятность ожидаемого числа "шестерок" равна:

Р (г

17) = "*^С„

(1/6)"

(5/6)*^

0,105 ,

что также маловеооятно.

154 */. 2. Анализ данных как составная часть принятия решений

Как же мы можем оценить, важна ли разница между этими вероятностями или

нет? Необходимы стандартные критерии, на основе которых мы можем сравнить

вероятности. Одним из таких критериев является общая вероятность всех исходов,

которая равна 1, то есть:

Р (все возможные исходы)=1.

Поскольку вероятность выпадения любой величины будет мала по сравнению

с 1, то процедурой, используемой на практике является сравнение Р (20 или более

"шестерок") с 1. Если Р (20 или более "шестерок") меньше 1, то мы утверждаем,

что если нулевая гипотеза верна, это событие маловероятно. В этом случае мы не

относим событие к статистической колеблемости или к случайности. Мы предпо-

лагаем, что имеется причина, которая пр1№ела к такому результату. Мы не знаем,

что это за причина, но самым резонным предположением является то, что на кость

оказывается влияние. Следовательно, мы отклоняем нулевую гипотезу, поскольку

нет оснований для ее подтверждения. Если Р(20 или более "шестерок") является

не маленькой по сравнению с 1, то событие могло произойти случайно. Нулевая

гипотеза не противоречит данным и, следовательно, не может быть отклонена.

Этот результат не доказывает, что нулевая гипотеза верна; мы просто говорим, что

нет оснований для ее отклонения.

Остается определить, что мы имеем в шщу под малой вероятностью. Эта та

отправная точка, на которую опирается лицо, принимающее р«пение, основываясь на

уверенности, требуемой для данного решения. Лицо, принимающее решение,

выбирает граничную величину для Р(20 или более "шестерсж"). Если действительная

величина вероятности болыпе, чем эта величина, то

ТЕИГда

нулевая гипотеза принимается.

Если действительная вероятность меньше, чем принятая граничная величина, решением

будет отклонение нулевой гипотезы. Лицо, принимающее решение, может выбрать

любую граничную величи^. Однако обычно используются следующие значошя:

Граничная величина для вероятности рИ),05. Если вероятность меньше

этого значения, то нулевая гипотеза может быть явно неверной. Мы не

доверяем этой гипотезе и отклоняем ее.

Граничная величина для вероятности р*Ю,01. Если вероятность меньше

этого значения, то более вероятно, что нулевая гипотеза неверна. Гипотеза

подвергается серьезному сомнению и отклоняется.

Граничная величина для вероятности р=0,001. Если вероятность меньше

этого значения, то нулевая гипотеза почти наверняка неверна и отклоняется.

Когда принимается решение, используется термин значимость. Например,

если решение необходимо сделать на границе 0,05 и действительная вероятность

меньше 0,05, то результат значим на уровне 5%. Это означает, что вероятность

случайного получения выборочной статистики большей или равной наблюдаемой

величины меньше 5%, следовательно, нулевая гипотеза находится под сомнением.

Однако, если действительная вероятность болыпе 0,05, то результат не значим для

уровня 5%. Вероятность случайного достижения выборочной статистики или большей

величины больше чем 5%, и кет причины для отклонения нулевой гипотезы.

Следует подчеркнуть, что несостоятельность отклонения нулевой гипотезы не

доказывает, что нулевая гипотеза верна. Существует много способов наблюде-

ния за выборкой статистических критериев, которые могут быть рассчитаны.

Гл.

Статистический

вывод 2:

испытание

гипотез 155

Некоторые из этих статистик будут согласовываться

нулевой гипотезой, некоторые

—

нет. Одни тесты дадут подгверя;дение, другие

—

опровержение. Лицо, приникающее

решения, должно оценить все доказательства и вынести свое личное суждение.

Вернемся к примеру с костью. Примем уровень значимости решения равным 5%.

Следующим шагом будет расчет вероятности достижения 20 или более "шестерок".

В результате мы получили Р (20 или более "шестерок")=0,2480. Теперь срав-

ним Р (20 или более "шестерок") с граничной величиной 0,05. Р (20 или более

"шестерок") больше 0,05, следовательно, можно сказать, что результат не сущест-

венен на уровне 5%. Доказательство согласуется с нулевой гипотезой. У нас нет

причины отклонить нулевую гипотезу. Вероятность достижения 20 или более

"шестерок" при бросании правильной кости равняется примерно 25%. У нас нет

оснований предполагать, что на кость оказывают влияние неслучайные факторы.

6.2.1.

Правила испытания гипотез

В принципе мы можем испытывать значимость любой статистики, имеющей любое

вероятностное распределение. Однако обычно мы сталкиваемся с несколькими

стандартными случаями. Выборочная статистика

—

средняя, доля и дисперсия

подчиняются либо нормальному, либо t, F или хи-квадрат-распределениям.

Проверка на основе нормального распределения. Этот критерий исполь-

зуется для испытания среднего значения выборки (х) по отношению к среднему

значению генеральной совокупности (ц). Такой критерий применяется при любой

величине выборочной совокупности (п), когда дисперсия генеральной совокупнос-

ти (а^) известна. Кроме того, если мы хотим тестировать выборочную долю р, то

можно использовать нормальное распределение, если величина выборки большая,

пр > 5 и п(1-р) > 5, поскольку в этом случае нормальное распределение дает

хорошее приближение к биномиальному распределению.

t-KpvrepHft. Используется для испытания гипотезы о среднем значении при

любой величине выборочной совокупности при неизвестной генеральной дисперсии.

Для больших выборок t-распределение приближается к нормальнс»!^ распределению.,

F-критернй. Используется для сравнения генеральных дисперсий. Размер

выборки может быть любым при условии, что выборка взята из нормальной

генеральной совокупности.

Критерий х-квадрат. Это непараметрический критерий, то есть значения

выборочной статистики не требуются. Этот Критерий основан на частоте появле-

ний значений случайных переменных. Может быть использован для испытания

гипотезы о связи между характеристиками или о согласии наблюдаемого частотно-

го распределения с некоторым стандартным распределением.

6.2.2. Одно-

двусторонние тесты

Как было уже отмечено, выбор уровня значимости, на котором принимается

решение, делается лицом, принимающим решения. Одним из важных аспектов,

который должен приниматься во внимание, является природа альтернативной

гипотезы. То, как задана альтернативная гипотеза, влияет на выбор границы

между критической областью и областью доверительных значений.

156

Ч. 2. Анализ данных как составная

часть

принятия решений

Вернемся к примеру, в котором машина производит металлические диски со

средним диаметром 2,0 см. Случайная выборка изготовленных дисков показала,

что средний диаметр равен 2,3 см. Если лицо, принимающее решения, просто

интересуется, правильно ли его машина настроена, то не важно, больше или

меньше выборочная средняя, чем предполагаемая средняя генеральной совокуп-

ности. Следовательно, нулевая и альтернативная гипотезы будут:

Нд.

|д =

2,0 см;

Hj : ц = 2,0 см.

Если принимается решение с

5%-ным

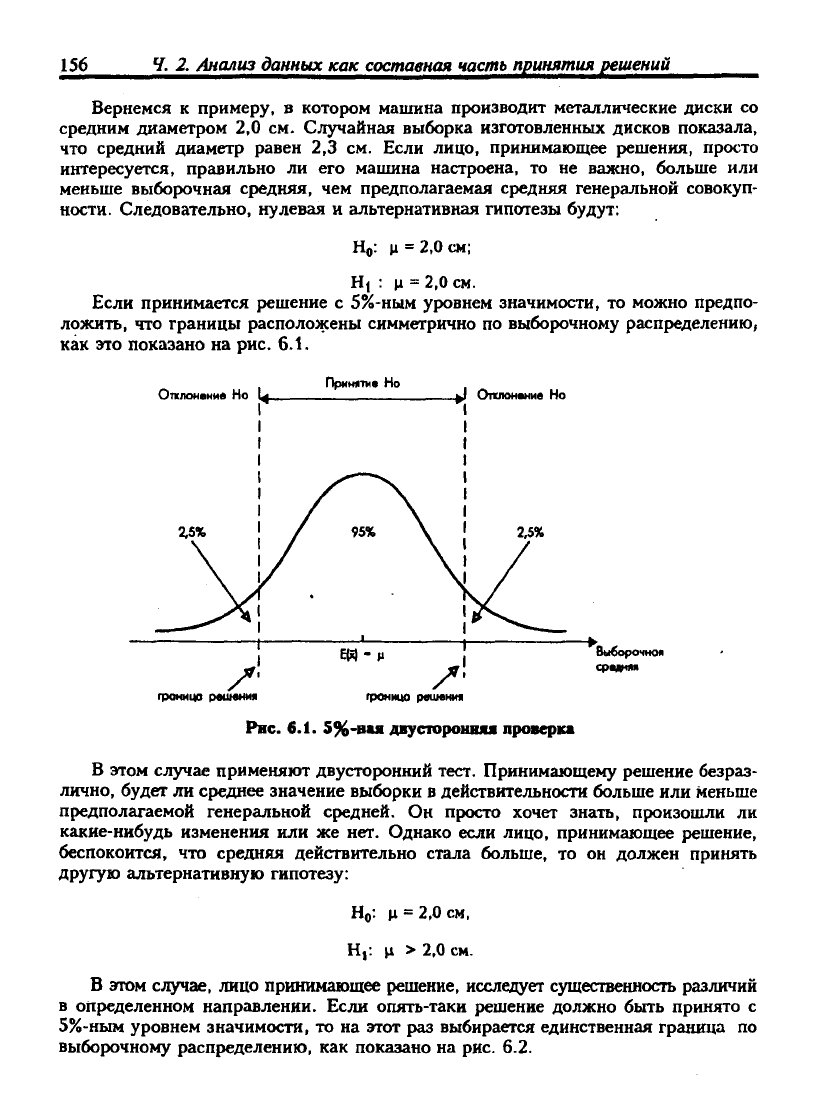
уровнем значимости, то можно предпо-

ложить, что границы расположены симметрично по выборочному распределению,

как это показано на рис. 6.1.

Отклонение Но

Примкти» Но

Отклонение Но

Выборочноя

срежнт

граница реипнии

Рис.

6.1.

5%-аая

джусторонши проверка

В этом случае применяют двусторонний тест. Принимающему решение безраз-

лично, будет ли среднее значение выборки в действительности больше или меньше

предполагаемой генеральной средней. Он просто хочет знать, произошли ли

какие-нибудь изменения или же нет. Однако если лицо, принимающее решение,

беспокоится, что средняя действительно стала больше, то он должен принять

другую альтернативную гипотезу:

Но:

ц = 2,0см,

Н,: ц > 2,0 см.

В этом случае, лицо принимающее решение, исследует существенность различий

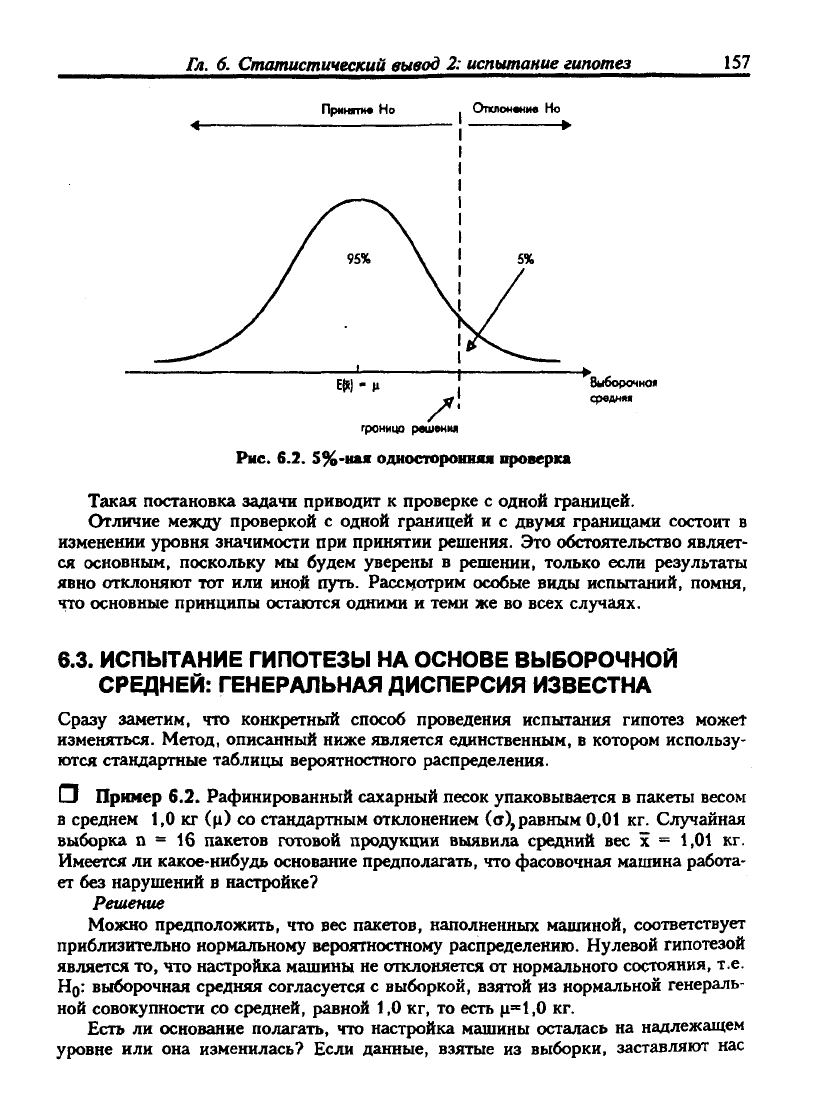
в определенном направлении. Если опять-таки решение должно быть принято с

5%-ным

уровнем значимости, то на этот раз выбирается единственная граница по

выборочному распределению, как показано на рис. 6.2.

Гл.

Статистический

вывод 2: испьтание гипотез 157

Прмнитш Но

Отклонение Но

Рнс.

6.2.

S%-iiax

одностороншш проверка

Такая постановка задачи приводит к проверке с одной границей.

Отличие между проверкой с одной границей и с двумя границами состоит в

изменении уровня значимости при принятии решения. Это обстоятельство являет-

ся основным, поскольку мы будем уверены в решении, только если результаты

явно отклоняют тот или иной путь. Рассмотрим особые виды испытаний, помня,

что основные принципы остаются одними и теми же во всех случаях.

6.3. ИСПЫТАНИЕ ГИПОТЕЗЫ НА ОСНОВЕ ВЫБОРОЧНОЙ

СРЕДНЕЙ:

ГЕНЕРАЛЬНАЯ ДИСПЕРСИЯ ИЗВЕСТНА

Сразу заметим, что конкретный способ проведения испытания гипотез может

изменяться. Метод, описанный ниже является единственным, в котором использу-

ются стандартные таблицы вероятностного распределения.

VJ Пример 6.2. Рафинированный сахарный песок упаковывается в пакеты весом

в среднем 1,0 кг (ц) со стандартным отклонением (а),равным 0,01 кг. Случайная

выборка п = 16 пакетов готовой продукции выявила средний вес х = 1,01 кг.

Имеется ли какое-нибудь основание предполагать, что фасовочная машина работа-

ет без нарушений в настройке?

Решение

Можно предположить, что вес пакетов, наполненных машиной, соответствует

приблизительно нормальному вероятностному распределению. Нулевой гипотезой

является то, что настройка машины не отклоняется от нормального состояния, т.е.

HQ:

выборочная средняя согласуется с выборкой, взятой из нормальной генераль-

ной совокупности со средней, равной 1,0 кг, то есть ц=1,0 кг.

Есть ли основание полагать, что настройка машины осталась на надлежащем

уровне или она изменилась? Если данные, взятые из выборки, заставляют нас

158

Ч.

Анализ данных

как

составная часть принятия решений

отклонить нулевую гипотезу, логично предположить, что машина работала при

неправильной настройке и, следовательно, альтернативной гипотезой является:

Н{:

выборка была взята не из нормального распределения со средней равной

1,0 кг, то есть ц *\

кг.

Из

следует, что выборочное распределение выборочных средних является

тоже нормальным распределением со средней, равной 1,0 кг, и стандартной

ошибкой, равной (0,01/VTF) кг. Проверим нулевую гипотезу при

5%-ной

значи-

мости, используя нормальное распределение с двумя границами (см. рис. 6.1.).

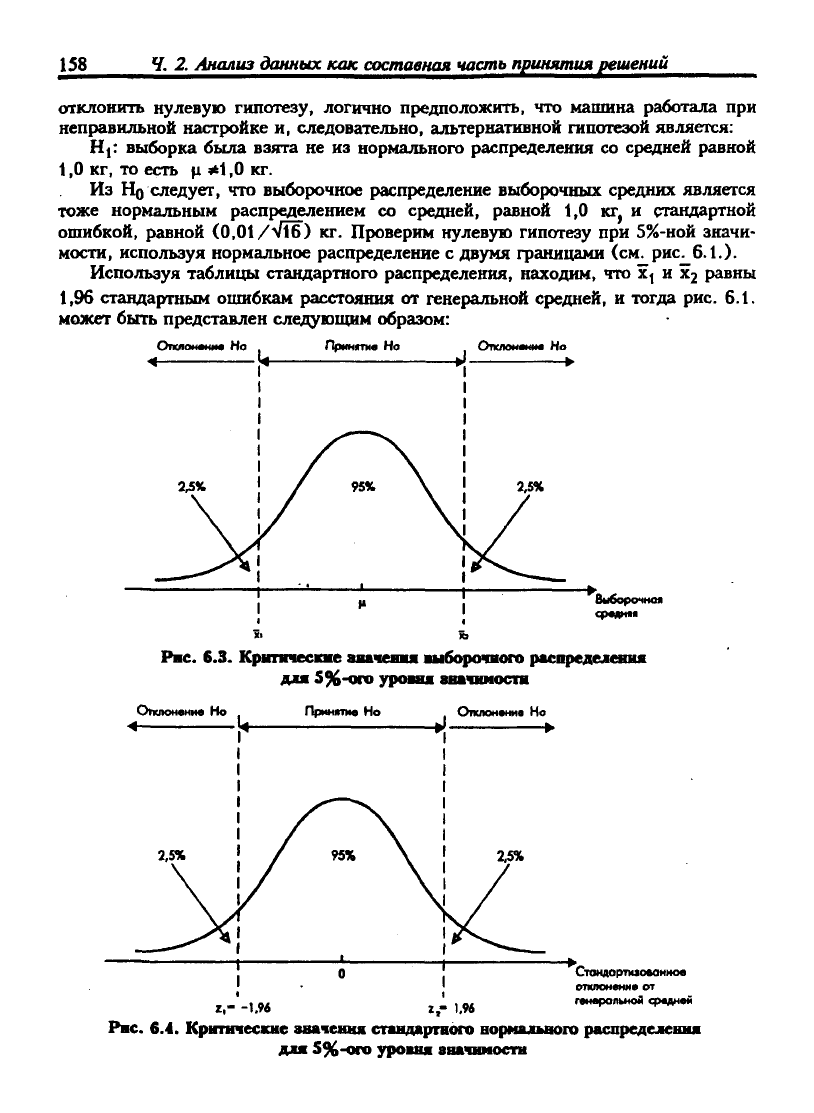
Используя таблицы стандартного распределения, находим, что х^ и Х2 равны

1,96 стандартным ошибкам расстояния от генеральной средней, и тогда рис. 6.1.

может быть представлен следующим образом:

Отклон«нм« Но .

•< Ч

Принятие Но

Отклоквн*м Но

J ^

Рнс. 6.3. Крнпрксте аиачеши шыборочшого распредедешш

дш

5%-ого

уровня автчииоега

Принитиб Но Олиюивнив Но

м •

Стоидортмзовоннов

опиюнониб от

z.-'-l.M z,-1,»6 г.«.ролы«Лср«н«

Рис. 6.4. Критические звачення епндартиого норнальвого распределения

для

5%-ого

уроввя авачниостн

Гл.

Статистический

вывод 2:

испытание

гипотез 159

Если теперь мы имеем значения выборочной средней х, равное 1,01 кг, то

можем выразить его отклонение от генеральной средней через количество стан-

дартных ошибок:

a/in'

SEj а/

Это то же самое выражение, которое использовалось в гл. 2, но стандартное

отклонение генеральной совокупности заменяется стандартной ошибкой выбороч-

ного распределения. Следовательно,

, 1,01 -1,0 .-

0.01/4

'^-^

стандартным ошибкам, которые лежат выше средней ц.

Значение стандартизованной переменной 4,0 больше, чем граничная величина

1,96. Это означает, что:

Р (стаидарггизованная переменная ^ 4,0) <

0,025

и результат существенен на

5%-ном

уровне значимости. Если мы нанесем на

диаграмму значение z=4,0, то оно попадает в область отклонения Н

д.

Поскольку

результат существенен на

5%-ном

уровне, мы приходим к заключению, что имеется

резонное основание, что выборочная средняя не согласуется с нулевой птокзой.

Мы отклоняем эту гипотезу в пользу альтернативной. Вероятность появления выбо-

рочной средней, равной 1,01 кг или больше, из-за случайных колебаний результа-

тов выборочного исследования в случайной выборке величиной

единиц, взятой из

нормальной генеральной совокупности, меньше чем 5%. Таким образом, мы счита-

ли,

что выборка была взята из генеральной совокупности, средняя которой была не

1,0 кг. Мы делаем вывод, что машина работала в условиях нарушения нормальной

настройки. Рассмотрим другой пример процедуры принятия решения.

IJ Пример 6.3. Штамповочный пресс делает отверстия в металлических шайбах.

В среднем величина отверстия ц = 4,00 мм со стандартным отклонением а = 0,20 мм.

Случайная выборка п = 25 шайб показала, что средний диаметр х - 3,88 мм.

Сохраняется ли нормальная настройка пресса?

Peuiefwe

Можно предположить, что диаметр отверстий, еделанных штамповкой, следу-

ет приблизительно нормальному распределению.

Нулевой гипотезой является то, что машина работает при правильной настройке.

HQ:

Выборочная средняя согласуется с выборкой, взятой из нормальной

совокупности со средней 4,0 мм, то есть ц °=4,0 мм.

Если данные выборки приводят к отклонению нулевой гипотезы, логично

предположить, что машина работает при неправильной настройке, то есть альтер-

нативной гипотезой является:

Н(:

Выборка не была взята из нормального распределения со средней 4,0 мм,

то есть ц * 4,0 мм.

160

Ч. 2. Анализ данных как составная

часть

принятия решений

Из HQ следует, что выборочное распределение выборочных средних также

является нормальным распределением со средней 4,0 мм и стандартной ошибкой

(0,2/V2F) мм. Из Hi следует, что мы будем проводить двустороннюю прюверку.

Примем решение относительно нулевой гипотезы на

1%-ном

уровне значимости.

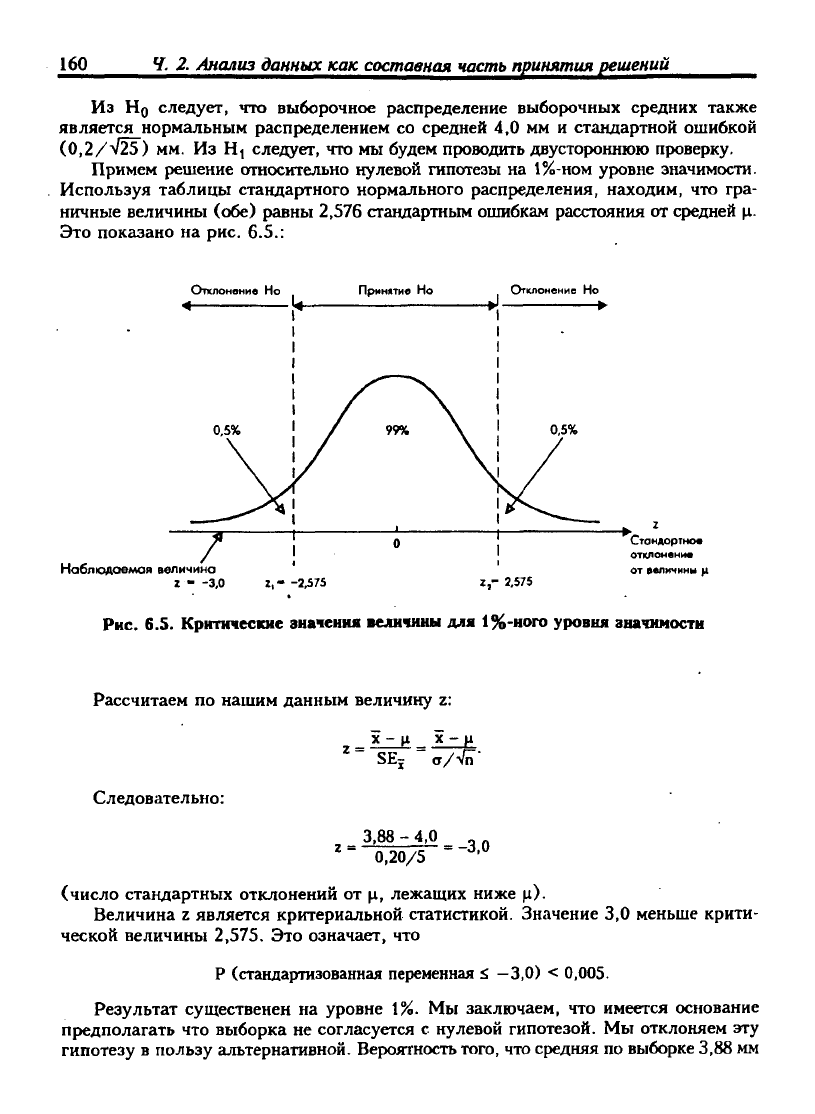
Используя таблицы стандартного нормального распределения, находим, что гра-

ничные величины (обе) {)авны 2,576 стандартным ошибкам расстояния от средней ц.

Это показано на рис. 6.5.:

Отклонение Но

< ,ч

Принятие Но

Наблюдоелдая величина

г - -3,0

Отклонение Но

*>.

•

Стондортное

отклонение

от ееличины ц

2,-

-2,575 г,- 2,575

Рис. 6.S. Критические значения величины для

1%-ного

уровня значимости

Рассчитаем по нашим данным величину z:

X - ц X - м

SE=

i/Vn'

Следовательно:

3.88-4,0,

0,20/5

•^•"

(число стандартных отклонений от ц, лежащих ниже ц).

Величина z является критериальной статистикой. Значение 3,0 меньше крити-

ческой величины 2,575. Это означает, что

Р (стандартизованная переменная 5 —3,0) < 0,005.

Результат существенен на уровне 1%. Мы заключаем, что имеется основание

предполагать что выборка не согласуется с нулевой гипотезой. Мы отклоняем эту

гипотезу в пользу альтернативной. Вероятность

того,

что средняя по выборке 3,88 мм

Гл.

6. Статистический вывод 2: испытание гипотез

161

или меньше из-за случайностей выборки 25 единиц, взятых из нормальной гене-

ральной совокупности со cpe^Hdi 4,0 мм, меньше, чем 1%. Следовательно, мы

делаем вывод, что настройка штамповочного пресса отклоняется от нормальной.

О Пример 6.4. Высота отдельных ростков рассады распределена нормально со

средней ц = 53 см и дисперсией о^ = 12 см^. В прошлом году в ящик, в кагором были

высажены а = 15 таких растений была внесена по ошибке двойная корма удобрения.

Средняя высота рассады в этом ящике достигла х '^ 55 см. Есть ли какое-либо

основание предполагать, что повышенное внесение удобрений дало положительный

эффект?

Решение.

Нулевой гипотезой является то, что дополнительное внесение удобрений не

дало эффекта.

HQ:

Выборочная средняя согласуется с выборкой, взятой из нормальной генераль-

ной совокупности со средней ц = 53 см. Есть ли основание предполагать, что

сверхудобрение не дало эффекта или, наоборот, способствовало росту растений?

Если мы репгаем отклонить нулевую гипотезу, логически предположим что сверх-

удобреиие дает положительный эффект и растения становятся очень высокими.

Таким образом, альтернативной гипотезой является следующая:

Н]:

Выборка не была взята из нормального распределения со средней 53 см, а

из генеральной совокупности со средней большей, чем 53 см, то есть ц > 53 см.

Из

следует, что распределение выборочных средних также является нормаль-

ным распределением со средней 53 см и стандартной ошибкой л/12/15 см. Из Hj

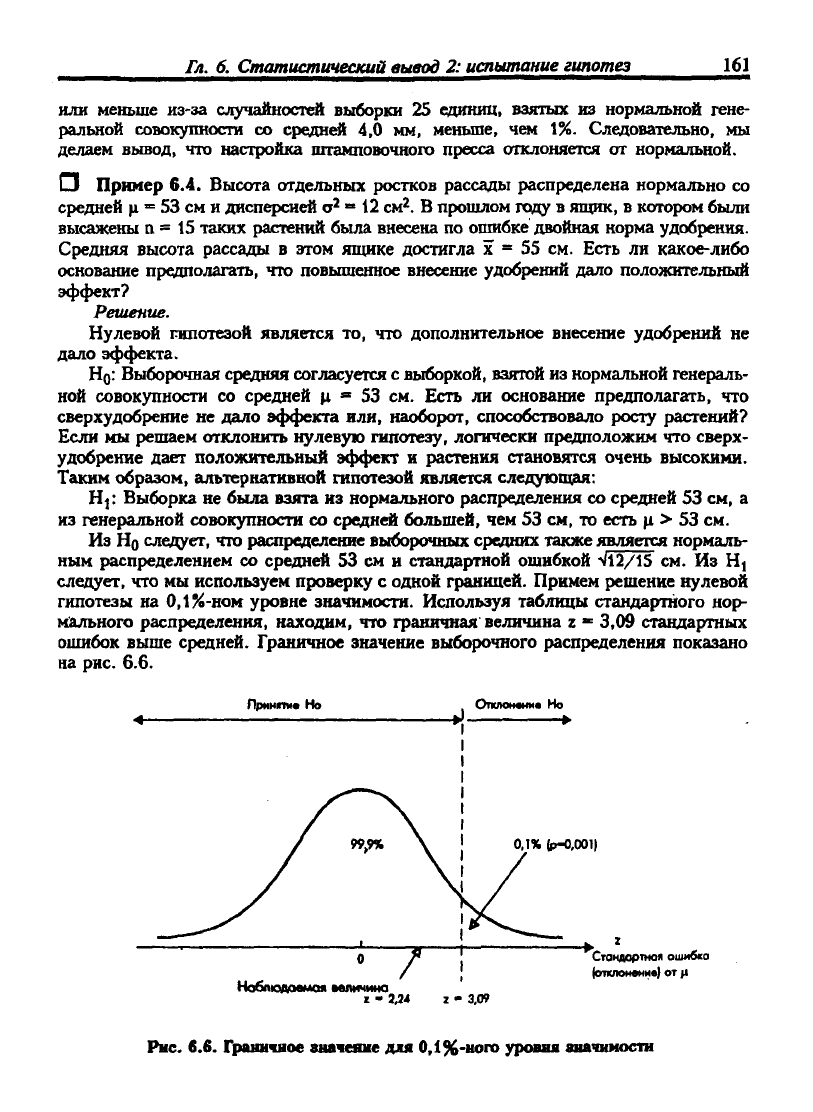
следует, что мы используем проверку с одной границей. Примем решение нулевой

гипотезы на 0,1%-ном уровне значимости. Используя таблицы стандартного нор-

мального распределения, находим, что граничная величина z ~ 3,09 стандартных

ошибок выше средней. Граничное значение выборочного распределения показано

на рис. 6.6.

Прингм*

Но

Олиюнвимя Мо

•

0.1%

Ь>-0,001|

Стандартноя ошибка

(отклонение) от ^

Рис. в.£. Граничное значение для 0,1%-ного уровня аначниости

162 Ч. 2. Анализ данных как составная часть принятия решений

Рассчитываем проверочную статистику z:

! ' 1

X •

SEj а/та'

Следовательно,

••

2,24 .

Рассчитанное значение z=2,24, меньше, чем граничная величина z = 3,09. Это

-означает, что:

Р (стандартизованная переменная г 2,24) >

0,001.

Результат не существенен при 0,1%-ном уровне значимости. Поэтому можно

заключить, что наблюдаемое явление согласуется с нулевой гипотезой, которую

мы принимаем. Вероятность появления выборочной средней 55 см или более из-за

случайностей выборки 15 наблюдений, взятых из нормальной генеральной сово-

купности со средней 53 см, больше чем 0,1%. Мы верим, что выборка взята из

генеральной совокупности, для которой средняя составляет 53 см, т.е. что вспомо-

гательное внесение удобрений не дало положительного эффекта.

6.4. ИСПЫТАНИЕ ГИПРТЕЗЫ

НА

ОСНОВЕ ВЫБОРОЧНОЙ

СРЕДНЕЙ — ГЕНЕРАЛЬНАЯ ДИСПЕРСИЯ НЕИЗВЕСТНА

В главах 4 и 5 мы встречались с положением, когда дисперсия генеральной

совокупности а неизвестна, в этом случае мы можем произвести ее оценку,

используя выборочное стандартное отклонение s. Тогда соответствующее стандар-

тизованное распределение становится t-распределением с (п1) степенями свободы.

О Пример 6.5. Компания "Britelite pic" производит электрические лампочки.

Для определенного типа лампочек установлен нормативный срок использования

ц =1500 ч. Для испытания новой партии была взята выборка п = 10 лампочек.

Среднее время пользования лампочкой в выборке равна 1410 ч х со стандартным

отклонением s = 90 ч. Свидетельствуют ли эти данные о том, что ожидаемый срок

использования изменился по сравнению с 1500 ч7

Решение

Нулевой гипотезой является предположение о том, что выборка была взята из

генеральной совокупности со средней 1500 ч.

Нд:

Выборочная средняя согласуется с выборкой, взятой из нормальной

генеральной совокупности со средней 1500 ч, то есть ц =1500 ч.

Н|: Выборка не была взята из нормально распределенной совокупности со

средней 1500 ч, то есть ц * 1500 ч. Из Hj следует, что мы будем использовать

испытание с двумя границами, из

—

что выборочное распределение выбороч-

ных средних также является нормальным распределением со средней 1500 ч и