Эддоус М., Стэнсфилд Р. Методы принятия решений

Подождите немного. Документ загружается.

Гл.

Выборка

выборочные распределения

133

Если мы произведем все возможные выборки объема п из нормально распреде-

ленной генеральной совокупности и вычислим выборочное статистики для каждой

из них, то сможем получить выборочное распределение для этой статистики. Эти

позволяет увидеть, как выборочная статистика связана с генеральным параметром.

Распределение всех выборочных средних, например, для выборки объемом п

единиц называется выборочным распределением выборочных средних.

Для нормальной COBOKJOIHOCTH выборочное распределение выборочных сред-

них (выборка объемом а) имеет математическое ожидание:

и стандартную ошибку.

Е (X) = ц - генеральную среднюю

^^^'^ (N-l)n •

где а — генеральная дисперсия в том случае, если объем выборки сравнительно

большой по отношению к объему генеральной совокупности N.

Если генеральная совокупность бесконечна или (n/N) 5 0,05, то:

SE^

•yf^.

На основе обобщения выборочных распределений мы можем по одной выборке

получить оценки генеральных параметров: ц =

'^ -у/ Д

где

д/Х>(х-х)' л л/1(х-х)'

S- у или о- V

==•

- 1

В последующих главах используются четыре главных распределения. Все они

основаны на предположении случайной выборки. Нормальное распределение z

описывает распределение выборочных средних, если генеральная совокупность

является нормальной:

j/^

Это распределение может использоваться и в том случае, если совокупность не

является нормальной, но выборка большего размера п ^ 30 в соответствии с

центральной предельной теоремой.

Если а не известна, но известно, что совокупность нормальна, стандартизован-

ное распределение выборочных средних описывается t-распределением, где t равно:

134 Ч. 2. Анализ данных как составная

часть принятия

решений

S/V (п - 1) w/Vir '

а t-распределение зависит от числа степеней свободы, которое определяется для

конкретной задачи.

Распределение х представляет распределение выборочных дисперсий в том

случае, если совокупность является нормальной:

2 S^

с (п-1) степенями свободы.

F—распределение описывает отношение двух выборочных дисперсий из двух

нормально распределенных совокупностей:

р^

"1*1 / °2^

(п,-1)о? (п2-1)о|'

Эти распределения табулируются различными способами и будут рассмотрены

в последующих главах.

УПРАЖНЕНИЯ

Упражнение 4.1

Являются ли данные следующих совокупностей конечными или бесконечными?

Заказы, выполненные прачечной за последнюю неделю.

Число сигналов опасности, которые были приняты пожарной бригадой.

Число голосов, зарегистрированных на выборах в городе.

Число заказов, которое могло быть выполнено с помощью инженерных работ.

Все

комш>юте[Я|1,

которые могли бы быть произведены в Озединенном Королевстве.

Упражнение 4.2

Укажите, что будет являться объектом исследования:

При изучении отношения общества к курению.

При изучении часовой заработной платы рабочих в обувной промышленности.

При изучении счетов компании в процессе аудиторской проверки года, окончив-

шегося в апреле 19... года.

При определении среднего срока службы электронного элемента.

Упражнение 4.3

Опишите, как могли быть получены основания для проведения выборки для

следующих обследований:

Гл.

Выборка

выборочные распределения

135

Домохозяйств в Отауне, которые обслуживаются почтовым отделением.

Студентов, которые в настоящее время обзгчаются в Университете Битой.

Адаокатов в Цитауне.

Рынков сбыта для розничной торговли электрическими товарами в Дитоне.

Упражнение 4.4

Объясните, почему следующие методы отбора данных могли бы привести к

ошибкам и нарушению случайности отбора в обследованиях, проводимых с целью:

Получить представление о взглядах общества на вивисекцию с помощью ответов

на вопросник, напечатанный в Журнале о природе.

Получить реак1шю общества на определенль^( метод налогооблажения проведе-

нием опроса при посещении домов в течение дня.

Выяснить отношение общества к проблеме проживания в центральной части

города по телефону, случайно выбирая абонентов.

Упражнение 4.S

В 4.4 этой книги идея выборочного распределения была проиллюстрирована на

примере выборок по две единицы из небольшой совокупности, состоящей из 6

чисел: 4, 8, 12, 16, 20, 24. Продолжим этот пример следующим образом.

Произведите 5 выборок по 4 единицы из этой совокупности.

Для каждой выборки из 4 единиц вычислите среднюю и стандартное отклоне-

ние.

Представьте в виде частотной диаграммы выборочные средние для всех выборок

объемом 2 единицы. Их значение возьмите 4.4.1. На тот же график нанесите

распределение выборочных средних для выборок по 4 единицы. Сравните

полученные диаграммы.

Постройте частотную диаграмму для стандартных отклонений для выборок

объемом по 2 единицы. Данные приведены в 4.4.2. На том же графике

представьте распределение выборочных стандартных отклонений для выборок

по 4 единицы. Сравните полученные диаграммы.

136

Глава 5. СТАТИСТИЧЕСКИЙ

ВЫВОД

ОЦЕНИВАНИЕ —

ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ

5.1.

ВВЕДЕНИЕ

В главе 4 рассматривалось, как выборка может быть использована для оценки

параметра генеральной совокупности. Мы также отметили, что в любой ситуации,

в которой используется такая оценка, необходимо иметь представление о её

надежности. Такую характеристику дает стандартная ошибка. Чем меньше стан-

дартная ошибка, тем меньше дисперсность выборочного распределения, и, следо-

вательно, менее изменчива выборочная статистика. Лучшим подходом к оценке

будет установление интервала значений, в пределах которого, как мы можем быть

уверены, лежит параметр генеральной совокупности. Этот предел значений назы-

вается доверительным интервалом. Доверительные интервалы могут быть уста-

новлены для любого параметра генеральной совокупности. Чаще всего они опре-

деляются для средних и относительных величин.

5.2. ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ ДЛЯ ГЕНЕРАЛЬНОЙ

СРЕДНЕЙ ц

5.2.1.

Генеральная дисперсия

а^

известна

Если исходная генеральная совокупность нормальная, то выборочное распределе-

ние выборочных средних также будет нормальным. Если генеральная совокуп-

ность имеет среднюю величину ц и стандартное отклонение а , то выборочное

распределение средних будет иметь среднюю величину, Е ( х ) = ц и стандартную

ошибку SE ; =

o/>ff.

Из центральной предельной теоремы известно, что данные

утверждения справедливы для ненормальной генеральной совокупности, если

объем выборки п не меньше 30.

Если мы отобрали п единиц из генеральной совокупности N и нашли среднюю

величину по выборке х, то х может быть использовано для оценки генеральной

средней ц. Насколько надежна эта оценка?

Гл.

5. Статистический вывод 1

137

95 % выборочного

роспредапении

CtQHoapTHox

ошибко

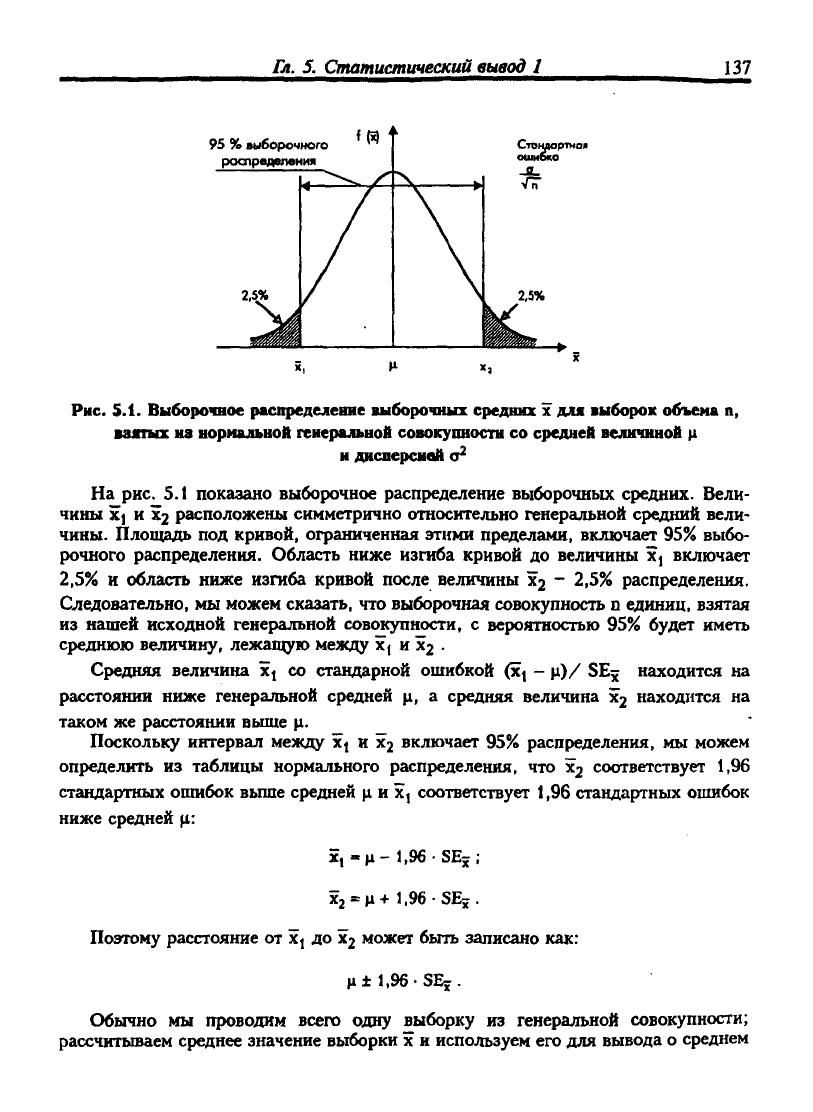
Рис. 5.1. Выборочное распределение выборочных средних х для выборок объема п,

взятых на нормальной генеральной совокупности со средней величиной д

н днсперснай

<т^

На рис. 5.1 показано выборочное распределение выборочных средних. Вели-

чины X] и Х2 расположены симметрично относительно генеральной средний вели-

чины. Площадь под кривой, ограниченная этими пределами, включает 95% выбо-

рочного распределения. Область ниже изгиба кривой до величины Х] включает

2,5% и область ниже изгиба кривой после величины Х2 ~

^,У/<>

распределения.

Следовательно, мы можем сказать, что выборочная совокупность п единиц, взятая

из нашей исходной генеральной совокупности, с вероятностью 95% будет иметь

среднюю величину, лежащую между х j и Х2 •

Средняя величина Х] со стандарной ошибкой (х^ - р)/ SE^ находится на

расстоянии ниже генеральной средней )i, а средняя величина Х2 находится на

таком же расстоянии выше р.

Поскольку интервал между х^ и Х2 включает 95% распределения, мы можем

определить из таблицы нормального распределения, что Х2 соответствует 1,96

стандартных ошибок вьпае средней р и Xj соответствует 1,96 стандартных ошибок

ниже средней ц:

X,-ц-

1,96 SEj,-

Х2

= Ц+ 1,96 SEj.

Поэтому расстояние от Х( до Х2 может быть записано как:

H±l,96SEj.

Обычно мы проводим всего одну выборку из генеральной совокупности;

рассчитываем среднее значение выборки х и используем его для вывода о среднем

138 Ч. 2. Анализ данных как составная часть

принятия

решений

значении генеральной совокупности ц, из которой была взята выборка. На

95%

мы

уверены, что наше единственное значение х лежит между Xj и Х2 . Если х

действительно попадает в интервал между х^ и Х2. то тогда ц должно находиться

где-нибудь в пределе:

x±t,96SEj.

Мы можем сказать, что уверены в этом на 9S%. Следовательно, х ± 1,96 • SEj^

является доверительным интервалом для среднего значения генеральной совокуп-

ности с вероятностью 95%. Если, например, х точно равно х^, то ц находится

правее точки х^. Если х меньше х^, то ц не лежит в доверительном интервале. В

этом слзгчае мы выбрали одну из 5% выборочных совокупностей, для которой

вывод, сделанный выше, неверен. Мы ограничились

95%

выборочного распределе-

ния. Это был совершенно субъективный выбор. Может быть использован любой

размер интервала и любая степень уверенности, что мы в нее попадем в зависимос-

ти от того, насколько мы хотим быть уверены, что среднее значение генеральной

совокупности лежит внутри указанного интервала. Типичными являются 90%, 95%

или 99%-ный доверительные интервалы. Какую бы величину мы не выбрали,

построение доверительного интервала остается тем же. Единственная разница

возникает в значении стандартизованной нормальной переменной z. Следователь-

но,

общая формула доверительного интервала для генеральной средней имеет вид:

± ^ /2

•

SE; ,

где z^ ^2 ~ величина стандартизованной нормальной переменной, выше которой

лежит (а/2)100% значений. Это дает (t - а)100% доверительный интервал.

Например, если нам требуется найти доверительный интервал с вероятностью

95%,

то тогда а = 0,05 и доверительный интервал может быть записан как:

* * ^.025

•

SE; .

Если известно стандартное отклонение генеральной совокупности то, тогда

стандартная ошибка распределения выборочных средних находится по формуле:

S Е;

а/^,

и (1 - а )100% доверительный интервал для генеральной средней может быть записан

как:

Пример 5.1. Импортер упаковывает чай в пакеты по 125 г. Известно, что

наполняющая машина работает со стандартным отклонением а, равным 10 г.

Выборка 50 пакетов п показала средний вес х = 128,5 г.

Гл.

Статистический

вывод 1 139

Найти доверительный интервал для среднего веса а в генеральной совокупности

с вероятностью

95%.

Предположим, что пакеты чая распределены по весу.

Решение.

Доверительный интервал с вероятностью

95%

для среднего значения генеральной

совокупности находится по формуле:

х±1,96 •^,

тле

1,96 является числом стандартных ошибок выше и ниже среднего значения для

интервала, включающего 95% нормального распределения. Следовательно, дове-

рительный интервал для генеральной средней находится как:

128,5

± 1,96

^ -

128,5

± 2,77 г.

Мы на 95% уверены, что средний вес пачки чая в генеральной совокупности

ц находится между двумя значениями: 125,73 г. и 131,27 г. Интервал в ± 2,77 г

составляет примерно ± 2% среднего веса пачки чая в выборке, который равен

128,5 г. Это не очень большое отклонение для данного примера. Следовательно,

среднее значение выборки может считаться надежной оценкой среднего значения

генеральной совокупности. Однако необходимо помнить, что в 5% случаев мы

можем ошибиться и получить значение вне доверительного интервала.

О Прииер S.2. Машина, которая упаковывает сахар, долгое время обеспечивала

нормальное распределение веса в наполняемых пакетах. Стандартное отклонение

веса а равнялось ± 2,5 г. Был установлен новый размер упаковок. Для контроля

была проведена случайная выборка 20 новых пакетов. Срезаний вес пакетов в

выборке

^ 1002 г. Предполагая, что переход на новую упаковку не повлиял на

колебаемость наполняемости пакетов, найдем доверительный интервал для среднего

веса упаковки в генеральной совокупности с вероятностью 99%.

Решение

Доверительный интервал для генеральное средней с вероятностью

99%

находится

следующим образом:

± 2.576 -?- ,

где 2,576 = Z — число стандартных ошибок выше и ниже среднего значения

соответствует интервалу, который включает 99% нормального распределения.

Тогда доверительный интервал с вероятностью 99% составит:

1002 ± 2,576

4| - 1002 ± 1,44 г.

Мы на 99% уверею!, что средний вес упаковки сахара ц генеральной совокуп-

ности находится в пределах от 1000,56 г до 1003,44 г. Размах в ±1,44 г составляет

примерно

±0,1%

среднего значения наполняемости в выборке (1002). 0,1% колеб-

яемости в весе упаковки невелико, следовательно, среднее значение выборки

140 Ч. 2. Анализ данных как составная часть принятия решений

может считаться точной оценкой среднего значения генеральной совокупности.

Следовательно, мы можем ошибиться в одном из 100 случаев и ц может оказаться

вне доверительного интервала.

5.2.2. Генеральная дисперсия неизвестна

Если дисперкгия в генеральной совокупности неизвестна, то тогда стандартная

ошибка выборочного распределения средних значений должна быть оценена сле-

дующим обр>азом (см. гл. 4.):

где

..лда;

выборочное стандартное отклонение;

л/Z^

(п-1)

—

несмещенная оценка стандартного отклонения генеральной совокупности.

Распределение соответствующей стандартизованной переменной далеко не

нормальное. В этом случае взамен нормального распределения используется t-pac-

пределение Стьюдента. (1 - а) 100% доверительный интервал для среднего

значения генеральной совокупности запишется как:

^±ta/2,(n-l) :^=у ИЛИ X±t„/j,(„_,) :^.

где t^/2 (п-1) ~ стандартизованная t-переменная для (п-1) степеней свободы,

выше которой лежит (а/2) 100% площади t-распределения.

В главе 4 отмечалось, что если объем выборки а, по крайней мере

равняется 30, то t-распределение можно считать тождественным нормальному

распределению.

а Пример S.3. Случайная выборка п = 25 пакетов яблок показала, что средний

вес пакета х равен 1020 г со стандартным отклонением s = 12 г. Найти доверитель-

ный интервал для среднего веса яблок генеральной совокупности с вероятностью

95%.

Предполагается, что генеральная совокупность нормальная.

Решение

Поскольку стандартное отклонение генеральной совокупности неизвестно, то

может быть оценена только стандартная ошибка выборки, t-распределение являет-

ся подходящим выборочным распределением. Доверительный интервал с вероят-

Гл.

Статистический

вывод 1 141

ностью 95% для среднего значения генеральной совокупности находится следую-

щим образом:

где t

д Д25

24 ~" стандартная t-переменная, выше которой находится 2,5% площади

t-распределения с (25 - 1)-степенями свободы. Используя таблицу t-распределе-

ния (см. приложение 2), находим, что:

* 0,025, 24 ~ 2,064.

Следовательно, доверительный интервал с вероятностью

95%'

составит:

1020 ± 2,064 ^Зт° 1020 ± 5,06 г.

На 95% мы уверены, что средний вес пакетов с яблоками в генеральной

совокупности ц находится в пределах от 1015 г до 1025 г.

Отклонение в ±5,06 г составляет приблизительно

±0,5%

среднего веса пакета в

выборке, равного 1020 г. Полученное выборочное среднее значение может считаться

надежной оценкой генеральной средней.

Г^ пример S.4. Производитель автомобильных шин заинтересован в получении

оценки средней износоустойчивости шин одной особой модели. Он провел случай-

ную выборку объемом 10 шин и подверг их специальному испытанию. Средняя

износоустойчивость по данным выборки оказалась равной 22500 миль со стандарт-

ным отклонением s = 3000 миль. Найдем доверительный интервал с вероятностью

99%

для средней износоустойчивости всего выпуска шин этого типа. Как обычно

предполагается, что генеральная совокупность нормальная.

Решение

Поскольку стандартное отклонение генеральной совокупности неизвестно, то

возможна лишь оценка стандартной ошибки выборочного распределения. Прини-

маем, что t-распределение является подходящим для использования стандартного

распределения. Доверительный интервал с вероятностью 99% для среднего значе-

ния генеральной совокупности находится следующим образом:

x±t

'•"^•'W^)'

где t

jjj g

—

стандартизованная t-переменная, выше которой находится 0,5%-ное

t-распределение с (10

—

1)-степенями свободы.

Используя таблицу t-распределения (см. приложение 2), находим:

* 0,005, 9 ~ 3,25.

Следовательно, доверительный интервал с вероятностью 99% составит:

142

Ч.

Анализ данных

как

составная часть принятия решений

22500 ± 3,25

^^ = 22500 ± 3250 миль.

Мы на

99%

ув^>ены, что средняя износоустойчивость

этого типа шин в

генеральной

совокупности ц находится в пределах между 19250 миль и 27750 миль.

Отклонение в ± 3250 миль составляет приблизительно ± 14% выборочной

средней износоустойчивости (22500 миль). Такое отклонение, по-видимому, явля-

ется слишком большим, и, следовательно, выборочное среднее значение износоу-

стойчивости может быть недостоверным для надежной оценки среднего значения

генеральной совокупности.

5.3.

ДОВЕРИТЕЛЬНЫЙ

ИНТЕРВАЛ ДЛЯ ГЕНЕРАЛЬНОЙ

ДОЛИ

(ОТНОСИТЕЛЬНОЙ ВЕЛИЧИНЫ) р

Нас обычно интересует оценка генеральной доли (пропорции) событий с некото-

рым характерным свойством. Например, аудиторов интересует доля ошибок в

с(»окупности счетов. Из главы 2 мы знаем, что доля событий, в которых возникает

характерное свойство, соответствует биномиальному вероятностно»ог распределению.

Однако если мы рассматриваем только большие выборочные совокупности и

случаи, в которых доля особых событий ни маленькая, ни большая, то мы можем

предположить, что выборочное распределение выборочной доли приблизительно

нормальное. Это означает, что можно найти доверительные интервалы для гене-

ральной доли, основываясь на нормальном распределении. Можно использовать

te же положения для этой аппроксимации, что и в разделе 2.8, где обсуждалась

•ормальная аппроксимация биномиального распределения^ при условии, что

np^S и п(1-р)2 5.

Обозначим генеральную долю событий р и р-выборочную долю. Стандартная

ошибка выборочного распределения доли особых событий

выборке находится по

следующей формуле:

SE;.

,ур(»-р).

Как было указано в разделе 2.3.3, это выражение является стандартным

отклонением биномиального распределения. Поскольку генеральная доля р обычно

неизвестна, стандартная ошибка будет оцениваться при использовании р как оцопси р:

Р п

Теперь мы можем найти (1 - а) 100%-ный доверительный интервал для гене-

ральной доли:

" ^ л/р (1-р )