Du C., Xie L. Modeling and Control of Vibration in Mechanical Systems

Подождите немного. Документ загружается.

54 Modeling and Control of Vibration in Mechanical Systems

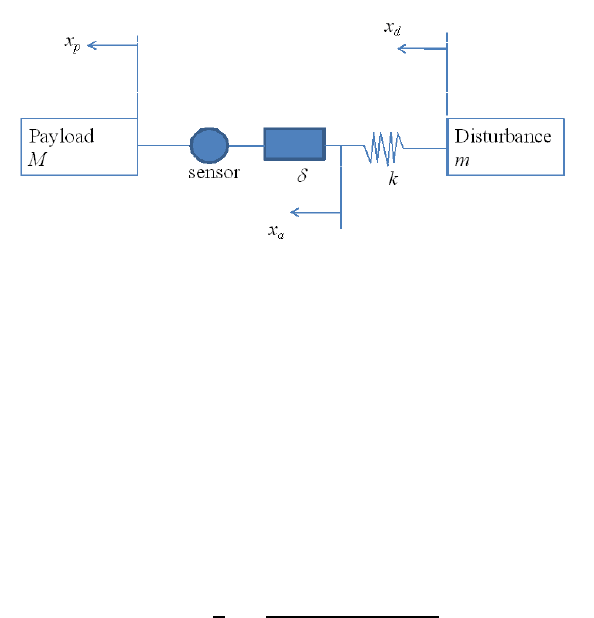
FIGURE 3.1

Single-axis system using piezoelectric stiff actuator.

= −ms

= k(x

−x

) = y (3.1)

and

δ = x

− x

. (3.2)

The transfer function between the extension δ of the piezo stack and the sensor

output y is

= k

Mms

+ k(M + m)

. (3.3)

Consider the piezoelectric hexapod integrated in a structure. Let M and K be the

mass and stiffness matrices of the global passive system, i.e., structure and hexapod.

The dy namic equati on governi ng the system is written as

x + Kx = Bf, (3.4)

where B is the fo rce Jacobian matrix, x represents payload frame disp lacement, and

f = kδ represents the equivalent piezoelectric force in the leg. A force sensor is lo-

cated i n each leg of the hexapod and collocated with the actuator. The corresponding

sensor output is

y = k(q − δ), (3.5)

where y is the force sensor outpu t and q is the leg extension from the equilibrium

position. Taking in to account the relationship between the leg extension and the

payload fr ame displacement

q = B

x, (3.6)

Modeling of Stewart Platform 55

the sensor output equation becomes

y = k(B

x − δ). (3.7)

The sensor output y is to be used as the input to the controller.

Next an adaptive ﬁltering approach will be used to model the hexapod Stewart

platform and verify the dynamics equati on (3.3).

3.3 Modeling using ad aptive ﬁltering approach

3.3.1 Adaptive ﬁltering theory

LMS algorithm

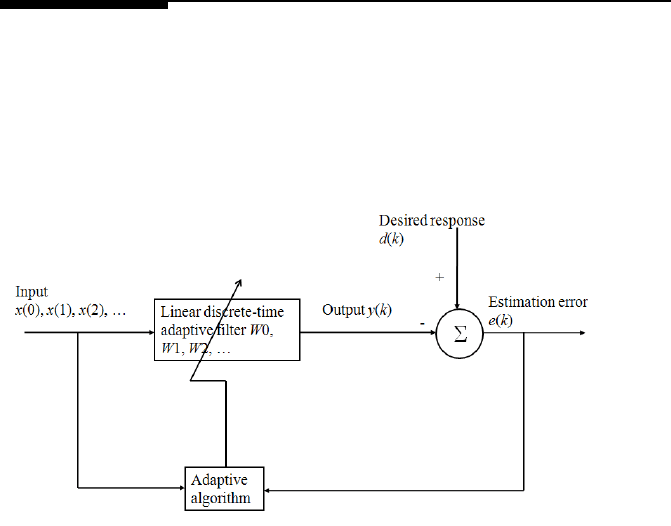
FIGURE 3.2

Linear discrete t ime adaptive ﬁlter.

In Figure 3.2, the statistically stationary time sequence of input signal, x(0), x (1),

···, is applied to the linear discrete time ﬁlter wh ose coefﬁcients are W 0, W 1, ···.

The ﬁlter out put at time k, y(k), is to be as close as possible to the desired response,

d(k). The difference between y(k) and d(k) is deﬁned as the estimation error, e(k)

that is then applied back to the ﬁlter to adjust the ﬁlter weig hts so as to minimize

the estimatio n error in the statistical sense. y(k) = W

(k)X(k), where W

(k) =

[W 0 W 1 W 2 ···], and X

(k) = [x (k) x(k − 1) x(k − 2) ···].

In most practical instances the adaptive process aims to minimize t he mean-square

value, or average power of the error signal [37]. Optimizatio n under this criterion is

56 Modeling and Control of Vibration in Mechanical Systems

most effective in stati stical sense. So the performance index of the adaptive ﬁlter is

determined by the mean-squared error (MSE) criterion in which the cost functi on is

deﬁned as follows.

ξ(k) = E[e

(k)], (3.8)

where E[ ] denotes the expected value.

e(k) = d(k) − y(k)

= d(k) − W

(k)X(k). (3.9)

ξ(k) = E[(d(k) − W

(k)X(k))

]

= E[d

(k)] − 2W

(k)E[d(k)X(k)] + W

(k)E[X(k)X

(k)]W (k)

= R

−2W

(k)R

+ W

(k)R

W (k), (3.10 )

where R

is the cross correlation function between d(k) and x(k), R

and R

are

respectively the autocorrelat ion functi ons of d(k) and x(k).

In many practical applications, the st atistics of d(k) and x(k) are unknown; the

exact knowledge o f gradient vector is not available. Thus t he metho d of steepest de-

scent [35] cannot be implemented in practical situations. Therefore another method

called the Least Mean Square (LMS) algorithm was introduced by Bernard Widrow

[37]. In the LMS algorithm, instantaneous squ ared error is used as an estimati on

of the mean squared error. The mathematical derivation of the LMS alg orithm is as

follows.

ξ(k) = e

(k),

∇

ξ(k) = ∇e

(k) = 2[∇e(k)]e(k),

e(k) = d(k) − W

(k)X(k),

∇e(k) =

∂e(k)

∂W (k)

= −X(k),

∇

ξ(k) = −2X(k)e(k). (3.11 )

The up dating equation of the adapt ive ﬁlter coefﬁcient:

W (k + 1) = W (k) −

∇

ξ(k),

becomes

W (k + 1) = W (k) + µX(k)e(k). (3.12 )

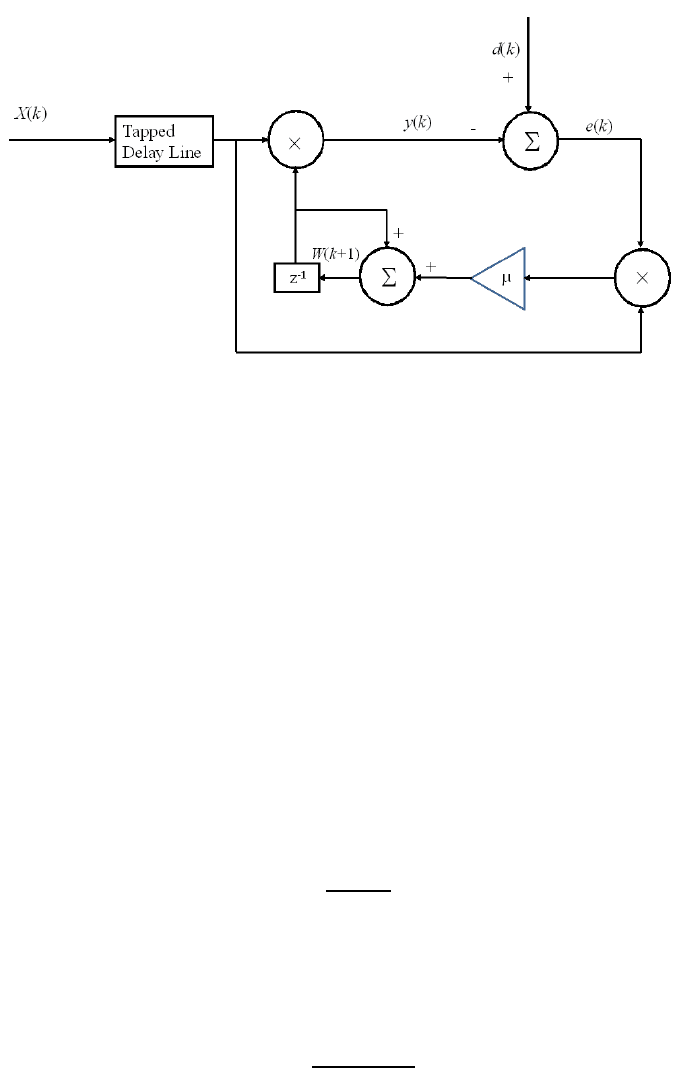
Modeling of Stewart Platform 57

FIGURE 3.3

Block diagram of the LMS adaptive ﬁlter.

Equation (3.12) is the well-known LMS algorithm th at is suitable for practical

signal processing applications because o f its simplicity and the availability of th e in-

stantaneous error in real time. The block diagram of the LMS al gorithm is illustrated

in Figure 3.3.

Normalized LMS algorithm

The LMS adaptation process is very much dependant on the step size µ and the

reference signal power. The step si ze determines the system convergence rate and

stabil ity [36][37]. The maximum stable step size is i nversely proportional to the ﬁlter

order L and the power of the reference signal x (k). A technique used to optimize

the convergence speed, independent of the reference signal power, is known as the

normalized LMS algorithm (NLMS).

The NLMS algor ithm is given as follows.

W (k + 1) = W (k) + µ(k)X(k)e(k), (3.13 )

where each variable is identical to the one for the LMS algorithm except for µ(k)

that is an adaptive st ep size computed as

µ(k) =

(k)

, (3.14)

where α is a normalized step size that satisﬁes 0 < α < 2, L is the ﬁlter length, and

(k) is the estimated power of the reference signal x(k).

The estimation of

(k) can be done using the mean square value of the reference

signal as follows.

(k) =

(k)X(k)

. (3.15 )

58 Modeling and Control of Vibration in Mechanical Systems

Then Equation (3.14) reduces to

µ(k) =

(k)X(k)

. (3.16 )

This step size is the most widely used for the NLMS algor ithm. A variant of the

NLMS alg orithm uses a small constant ε as follows.

µ(k) =

ε + X

(k)X(k)

. (3.17)

This con stant ensures that the step size does not tend to inﬁnity in the case of a

zero input signal.

The NLMS algori thm guarantees an attenuation level of γ ≤ 1, where γ is the

induced-norm from noise or signal inputs to the ﬁltering error. Therefore, a salient

feature of this algorit hm is that it lowers t he inﬂuence o f the input signal on the no ise

ampliﬁcation effect, especially when t he input signal x(k) is large.

3.3.2 Modeling of a Stewart platform

Adaptive identiﬁcation is a technique th at uses an adaptive ﬁlter to model an un-

known system. An adaptive identiﬁcation method can be applied either online along

with the vibration control or ofﬂine pri or to the vibration control. In an onlin e identi-

ﬁcation system, the number of adaptive ﬁlters required for an adaptive control system

will be increased. Furthermore, convergence of the adaptive ﬁlter used in the identi-

ﬁcation section of the system can be affected by a large amount of primary vibration

signal [36]. Therefore an ofﬂine identiﬁcation technique will be applied for the sys-

tem mod eling.

The block diagram of the adaptive identiﬁcation is illustrated in Figure 3.4. P (z)

is the transfer function of the system to be identiﬁed. W (z) is a digital ﬁlter used

to model P (z) based on the LMS error minimization algorithm. Both systems P (z)

and W (z) are excited by a band limited white noise. The difference between the

two outputs d(k) and y(k) is fed back into the LMS algorithm as error signal e(k).

The LMS algorithm will adaptively adjust the coefﬁcients of ﬁlter W (z) to minimize

e(k) based on the least MSE criterion. When the error signal reaches the minimum

level, the ﬁlter W (z) r epresents a model of P (z).

The LMS adaptive ﬁlter approach is applied for the modeling of the Stewart plat-

form. A Simulink program is developed for ofﬂine identiﬁcation of the platform.

A 16th order LMS adaptive ﬁlter with adaptation step size of 0.01 is chosen. A

band-limited white noise is used as the training signal. Sampling frequency of the

white noise generator is set at 1 kHz so that the response of the PZT actuator will be

conﬁned to the bandwidth of 500 Hz (half o f sampling frequency). But the sampling

frequency of the adaptive ﬁlter is set to 10 kHz to give enough time for adaptive ﬁlter

to compute the ﬁlter weights within each sample of the training signal .

The Simulink pr ogram for the identiﬁcation is downloaded into a dSPACE real

time interface board DS1104. Identiﬁcation process for each PZT actuator is per-

formed alternatively. Filter tap values are recorded throug h the dSPACE manager

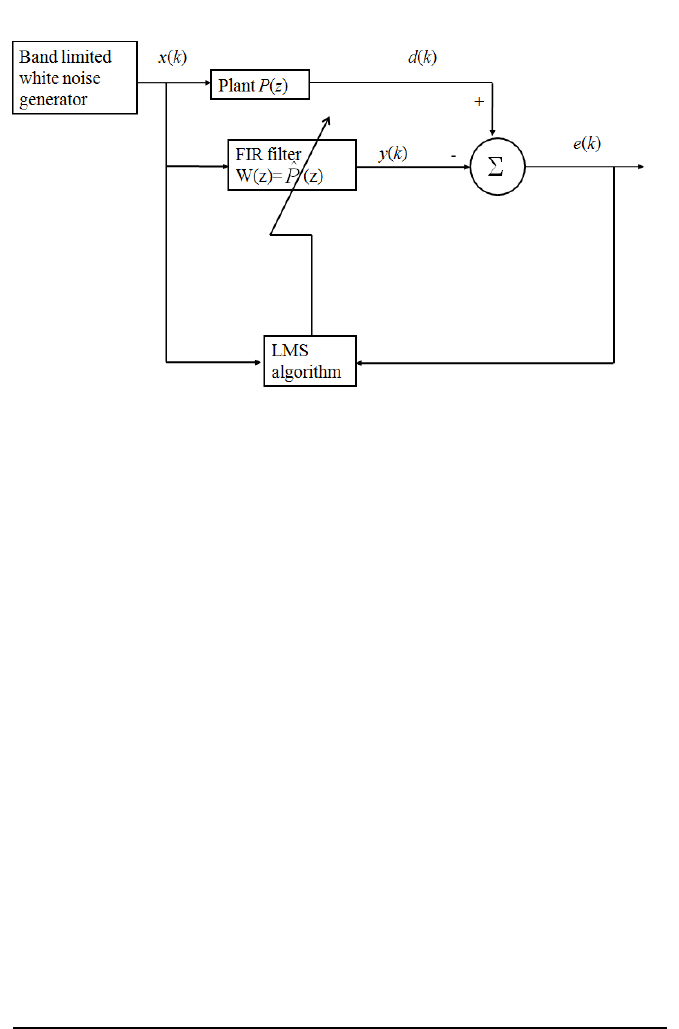
Modeling of Stewart Platform 59

FIGURE 3.4

System identi ﬁcation u sing LMS adaptive ﬁlter.

software during the identiﬁcation process. From the results of the identiﬁcation of

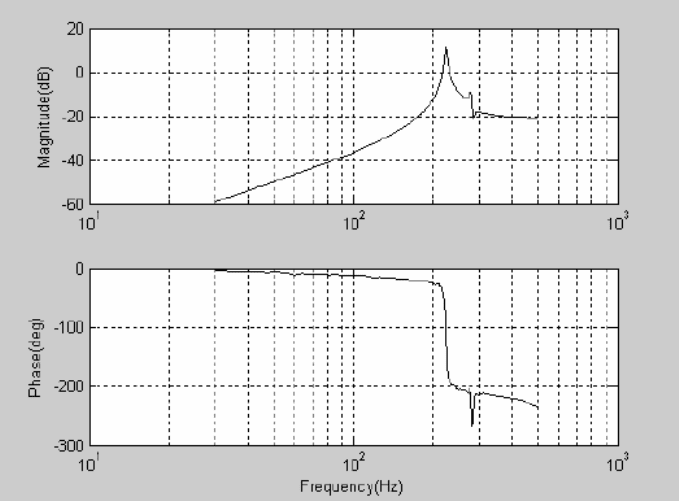
six PZT actuators of the Stewart platform in Figure 1.2, one of the resonance fre-

quencies of the smart structure is found to be around 240 Hz. Figure 3.5 is the phase

and magnitude responses of one of the six PZT actuators. The result shows that there

is a resonance peak at about 240 Hz. The ph ase response between 60 Hz and 200

Hz i s approximately linear. Experimental results of the active vibration control sy s-

tem also indicate that the frequency region that can attenuate the vibration signal i s

between 60 Hz and 220 Hz.

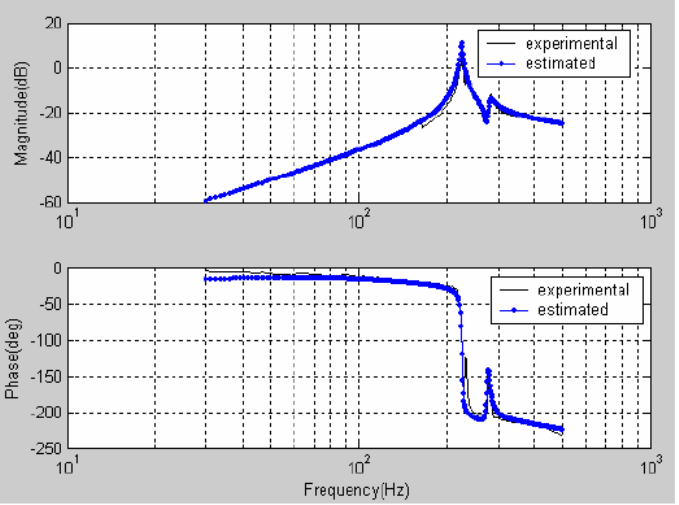
By applying a frequency domain modeling approach, an approximate model in

terms of a transfer fun ct ion for each leg can be obtained. Figure 3.6 shows the fre-

quency responses of an PZT actuator, including the estimated and the experimental

ones. It is clearly shown that the estimated transfer f unction is well ﬁtted to th e real

one. It is also noted that the shape o f the frequency responses in Figure 3.6 agrees

with that of the model in (3.3).

The transfer function of the PZT actuator i s obtained as:

P (s) =

−190.9s

−1.499 × 10

−5.703 × 10

− 2.507 × 10

s − 5.624 × 10

+ 3232s

+ 5.378 × 10

+ 1.621 × 10

+ 6.82 ×10

s + 1.943 ×10

(3.18 )

60 Modeling and Control of Vibration in Mechanical Systems

FIGURE 3.5

Frequency responses of a PZT actuator.

Modeling of Stewart Platform 61

FIGURE 3.6

Estimated and experimental frequency responses.

62 Modeling and Control of Vibration in Mechanical Systems

3.4 Conclusion

This chapter has studied the modeling of an active piezoelectric Stewart platform.

The LMS adaptive ﬁlterin g approach has been adopted for the system identiﬁcation.

The model obtained via the adaptive identiﬁcation or the experimental testing has

shown consistency with the governing mot ion equation.

Classical Vibration Control

4.1 Introduction

The presence o f vibration often leads to undesirable effects such as structural o r

mechanical failure, frequent and costly maintenance of machines, worsening posi-

tioning performance, and human pain and discomfort. Vibrations can sometimes be

eliminated theoretically. However, due to the high manufacturing cost that may be

involved in eliminating vibration , reduction of vibrati on is preferred so as to achieve

a compromise between an acceptable amount of vibr at ion and a reasonable manu-

facturing cost . Various cl assical techniques of vibration contr ol for the purpose of

vibration reduction have been presented, such as balancing of rotating and recipro-

cating machine, contro l of natural frequency, damping and stiffness modiﬁcation,

isolat ors, and absorbers. Some of the techniques will be introduced brieﬂy in this

chapter.

An active vibratio n control is required for a system if it needs an external power

to perform it s function. Examples of some active v ibration control include, (1) usi ng

hybrid mass dampers to apply a control force to a movable mass so as to reduce

building sway caused by wind and seismic waves, (2) reducing aircraft cabin noise

by attenuating the vi bration of the large panels of thin metal that form the cabin

walls, (3) damping out vibrations using piezoelectric devices installed on the trailing

edge of helicopter blades, etc.

4.2 Passive control

4.2.1 Isolators

Vibration isolation methods are used to reduce the undesired effects of vibration. It

involves the insertion of a resilient member called an isolator between the vibrating

mass and the source of vibration so that a reduction in the dynamic response of

the system is achieved under speciﬁed conditions of vibration excitation [4]. A n

isolat ion system is said to be active or passive depending on whether or not external

power is required for the isolator to perform its function. A passive i solator consists