Du C., Xie L. Modeling and Control of Vibration in Mechanical Systems

Подождите немного. Документ загружается.

24 Modeling and Control of Vibration in Mechanical Systems

−60

−50

−40

−30

−20

−10

Frequency(Hz)

Magnitude(dB)

FIGURE 2.4

Multiplicative uncertainty of a VCM.

Modeling of Disk Drive System and Its Vibration 25

roughly classiﬁed into two categories: static models and dynamic models. There

are various static models for friction, for example, the Coulomb model, the viscous

model, and friction models with t he Stribeck effect, etc. However, a static friction

model cannot capture observed friction phenomena like hysteresis, positio n depen-

dence, and variations in breakaway forces. Therefore, a friction model involving

dynamics is necessary to describe friction phenomena accuratel y. A rel at ively new

dynamic friction model proposed in [43] combines the Dahl stiction behavio r with

arbitrary steady state frict ion characteristics, which is able to include the Str ibeck

effect. A nonli near friction observer is then required for position control because

the involved interim state is not measurable and has to be observed in order to es-

timate the friction fo rce. Later, to overcome the limitations of the above model, an

integrated model is proposed in [44], which is used in [41] for VCM pivot friction

modeling in HDDs. The resultant friction model needs to be iteratively impr oved and

veriﬁed using the measured and the simulated responses. Another dynamic model

used in VCM pivot friction modeling is the preload and two-slope model, which is

detailed in [40, 42] respectively in the frequency domain and the time domain. How-

ever, although the time-domain approach provides a good match between the time

domain response of the model and the data collected, it cannot guarantee a good

match in the frequency domain, and vice versa.

The non-model based appr oaches include the neural network method [46][47] and

the disturbance observer method [45]. The neural network method does not require

full knowledge of t he no nlinearity model, but its implementation in real di sk drives

seems difﬁcult because of sl ow convergence [48]. In [45], a novel method for the

cancelation of pivot n onlinearities is proposed and it consists of an accelerometer

and a disturbance observer. The accelerometer is employed to linearize the dynam-

ics fr om the desired input signal to carriage angular acceleration, and the observer

estimates the nonlinear disturbances d ue to pivot friction for disturbance cancelation.

In this sectio n, a mathematical model will be developed to closely describe the

friction hysteresis behavior. Among existing hysteresis models in the literature, the

Prandtl model [50] is less complex and more attractive in real-time applications. The

element ary operator in the Prandtl hysteresis model is a rate-independent backlash

or linear play operator, deﬁned by p

(π

, x(t)), where x(t) is the actuator response

and π

∈ R is usually initialized to 0. Hysteresis nonlin earity can b e modeled by a

linearly weight ed superposition of many backlash operator s with different threshold

r > 0 and weight values w

, i.e.,

(x(t)) =

∞

(r)p

[π

, x(t)]dr, (2.15 )

where the weight w

deﬁnes the ratio of the backlash operator, as seen in Figure 2.5.

In order to have an accurate mathematical model for the hysteresis, th e creep model

proposed in [49] is al so incorporat ed. Hence we consider the operator model given

F (x(t)) = ax(t) +

∞

(r)p

[π

, x(t)]dr +

∞

(λ)l

[ξ

, x(t)]dλ,

26 Modeling and Control of Vibration in Mechanical Systems

(2.16 )

where t ∈ [0, T ], a, w

(r) and w

(λ) are parameters to be determined, p

and l

are

the elementary hysteresis and linear creep operators, and are deﬁned as follows.

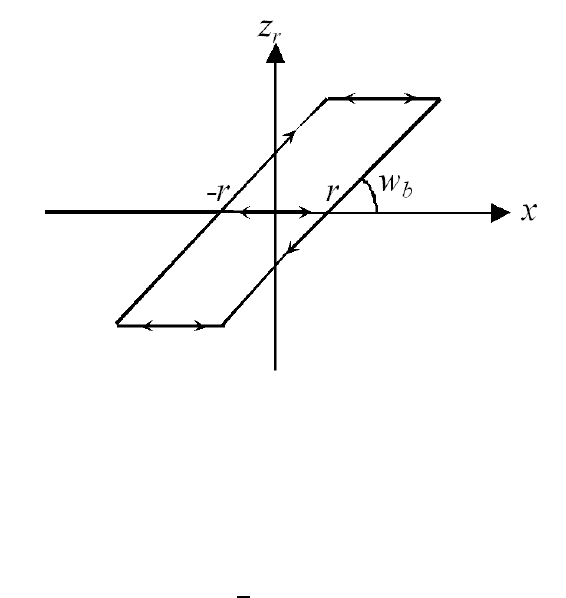
The elementary h ysteresis o perator p

with threshold r is d eﬁned as the solution

operator p

[π

, x(t)] = z

(t) o f the rate in dependent hybrid differential equation

˙z

(t) =







˙x(t), if x(t) = z

(t) − r

0, if z

(t) − r < x(t) < z

(t) + r

˙x(t), if x(t) = z

(t) + r

with the init ial value

(0) = max{x(0) − r, min{x(0) + r, π

(r)}}. (2.17 )

FIGURE 2.5

The op erator z

versus x.

Deﬁne the linear creep operator l

with λ > 0 as the solution operator l

[ξ

, x(t)] =

(t) o f the differential equation

˙z

(t) + z

(t) = x(t) (2.18 )

with the init ial value equation

(0) = ξ

(λ).

Modeling of Disk Drive System and Its Vibration 27

The explicit integral formula for the linear creep operator l

is as foll ows.

[ξ

, x(t)] = e

−λt

(λ) + λ

λ(τ−t)

x(τ)dτ. (2.19 )

For numerical implementation of t he operator-based modeling, a discrete-time

model F (x(k)) of the operator F (x(t)) in (2.16) is developed as fo llows.

F (x(k)) = ax(k) +

i=1

[π

, x(k)] +

j=1

[ξ

, x(k)], (2 .20)

where

1) the output sequence of the discrete hysteresis operato r is calculated by

[π

, x(k)] = z

(k), (2.21)

(k) =







x(k) + r

, if z

(k − 1) − r

≥ x(k)

(k − 1), if z

(k − 1) − r

< x (k) < z

(k − 1) + r

x(k) − r

, if z

(k − 1) + r

≤ x(k)

with the init ial value z

(0) = max{x(0) − r

, min{x(0) + r

, π

)}};

2) t he discrete counterpart to the continuou s elementary creep operator is given by

[ξ

, x(k)] = z

(k) (2.22 )

with

(k + 1) = e

−λ

· z

(k) + (1 − e

−λ

) · x(k) (2 .23)

and the initial value z

(0) = ξ

(λ

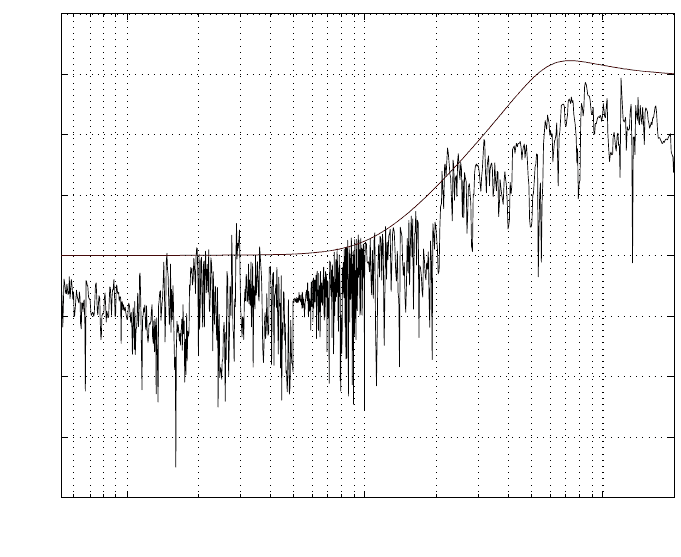
Consider the hysteresis curve of the frictio n f versus the displacement x in Figure

2.6. Let f

= F (x(k)) be the approximated friction, then the approx imation erro r

e = f −f

. We deﬁne the energy gain between the actuator position and the error as

∞

k=1

(k)e(k)

k=1

(k)x(k)

, (2.24 )

where L is the number of d at a points.

Denote w

= (w

, w

, ···, w

), w

= (w

, w

, ···, w

), and Λ = (λ(1),

λ(2), ···, λ(m)). We aim to ﬁnd optimal parameters a, w

, w

, and Λ in (2.20) so

that (2.24) is minimized, and thus a model (2.20) can be obt ai ned to approx imate the

friction f with the displacement x as t he input.

Note that kT

∞

is a function of a, w

, w

, and Λ, and is denoted as

∞

= ℓ (a, w

, w

, Λ) . (2.25)

The MATLAB fun ct ion fminsearch can be used to minimize ℓ (a, w

, w

, Λ) with

respect to (a, w

, w

, Λ).

28 Modeling and Control of Vibration in Mechanical Systems

FIGURE 2.6

Fricti on f versus actuator displacement x.

FIGURE 2.7

A PZT actuated suspension.

Modeling of Disk Drive System and Its Vibration 29

2.3.3 Modeling of a PZT microactuator

A piezoelectric-based microactuator located on the suspension as shown in Figure

2.7 is considered in this section. The mechanical operati on of th e microactuator

can be understood via an equivalent spring- mass system. The compliance of the

base plate is simpliﬁed as a single spring K

, and the compliance of the ﬂex hinge

element s is simpliﬁed as a single rotational spr ing K

FIGURE 2.8

Equivalent spring mass system of PZT microactuator.

An import ant point for PZT microactuato r modeli ng is that the PZT element acts in

series wi th the b ase plate springs. Thus the displacement o f th e PZT element results

in displacements of the springs. The PZT and the base plate wi th spring constants

and K

can be equivalent to a single spring with constant

. (2.26)

The model is derived b y applying forces at the interface of the piezo element and

the base plate sprin g and b y summing moments abou t the pivot point. The free

expansion of the piezo element is expressed as

exp

, (2.27 )

30 Modeling and Control of Vibration in Mechanical Systems

where L

is the piezo leng th, d

exp

is the piezo expansion coefﬁcient, V is the volt-

age, c is the piezo thickness, and l

is the length as indicated in Figure 2.8.

The following second order differential equation can be derived to capture the

dynamic behavior of the microactutor:

+ C

dθ

+ (K

+ K

)θ =

exp

V, (2.28 )

where K is the torsio nal inertia, K

is the torsional spring rate. A typical frequency

response of the PZT microactuator from volt age input to position output is shown in

Figur e 2.9.

−30

−20

−10

Magnitude(dB)

−200

−160

−120

−80

−40

Phase(deg)

Frequency(Hz)

FIGURE 2.9

A typical frequency response of the PZT microactuator.

2.3.4 An example

2.3.4.1 Dynamics modeling

The hard disk drive und er consideration is sh own in Figure 2.10. It includes the VCM

actuator mounted with the arm and the suspension/head. The actuator i s driven by a

driver which converts voltage differences into current differences l inearly.

The actuator dynamics measurement is taken using a Laser Doppler Vibrometer

(LDV) and a Dynamic Signal Analyzer (DSA). The displacement y i s measured via

Modeling of Disk Drive System and Its Vibration 31

FIGURE 2.10

An opened 1.8-inch hard disk drive.

the LDV, and the frequency response is measured by using the DSA to generate a

swept sine sign al to excite the actuator. The measured frequency response is shown

in Figure 2.11 , where the modeled one is plotted from t he following transfer function

P (s) obtained by curve ﬁtting to the measured frequency responses.

P (s) = KP

(s)P

res

(s), K = 5.3290 ×10

(s) =

+ 2 × 0.25 × 2π120s + (2π120)

res

(s) =

+ 1081s + 7.3 × 10

+ 1056s + 6.964 ×10

)(s

+ 6032s + 2.527 ×10

)

. (2.29)

The resonance of P

(s) at 120 Hz is due to the nonli nearity of actuator pivot

friction. When the friction nonlinearity is neglected, it is replaced with the pure

double integrators model, i.e.,

P (s) =

res

(s), K = 4.8209 ×10

, (2.30 )

which is plotted as the dotted curves in Figure 2.11. However, the friction in the

actuator pivot [39] [40] is known to limit the low frequency gain of the control loop.

Translated to the error rejection function or sensitivity fu nction, it lif ts the magnitude

32 Modeling and Control of Vibration in Mechanical Systems

−40

−20

100

Magnitude(dB)

−600

−400

−200

200

Frequency(Hz)

Phase(deg)

Measured

Modeled

FIGURE 2.11

Measured and modeled frequency responses of the VCM actuatio n system (LDV

range 0.5 µm/V).

Modeling of Disk Drive System and Its Vibration 33

of the sensitivity function at low frequencies, and thus reduces the ability of the

control loop to reject low-frequency vibrations and affects the positioning accuracy.

Therefore, it is necessary to compensate the friction impact.

2.3.4.2 Friction measurement and modeling

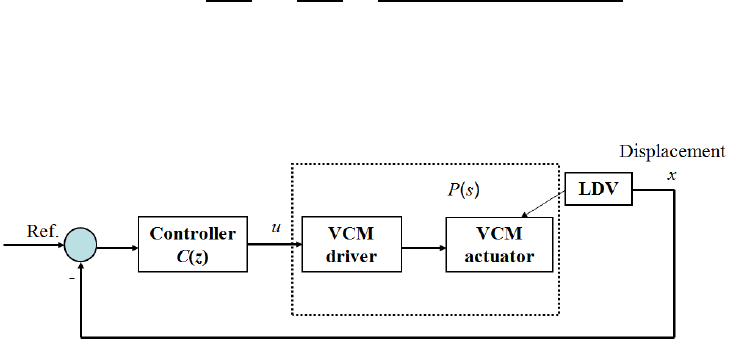
Due to t he ﬂuctuation of the head when the d isk is rotating (rotational speed is 4200

RPM), it is difﬁcult to have a steady displacement signal of the head. Thus the

friction measurement is carried out under the closed loop control as sh own in Figure

2.12. The control ler C(z) is a PI D control ler combined with a notch ﬁlter and is

expressed in (2.31). The sampling time T

is 83.3 ms. With the controller, the open-

loop 0 dB crossover frequ ency is 945 Hz, the gain margin is 8.7 dB, and the phase

margin is 49 deg.

C(z) = k

+ k

z − 1

+ k

z − 1

) ×

0.9023z

+ 0.9467z + 0.724 2

+ 0.929z + 0.6442

= 0.0625, k

= 0 .8, k

= 400 × 10

−6

, k

= 400. (2. 31)

FIGURE 2.12

Closed control loop of a disk drive with a VCM actuator for frict ion measurement

via LDV.

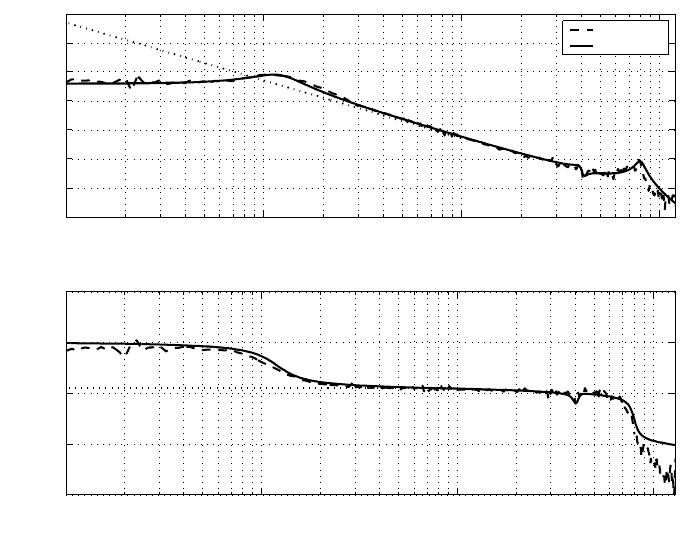
A 10 Hz sinusoidal signal w ith increasing amplitude of 0.5, 1 , and 3 V is r e-

spectively used as the reference signal in Figure 2.12. The control signal u and

displacement x are measured, and shown in Figure 2 .13.

The VCM actuator model with consideration of nonlinearity F (x) is shown in

Figur e 2.14, which includes two pure integrators, the resonance modes P

res

(s) and

the gain K given in (2.30).

With the measured u and x, u

can be obtained from x, and thus f = u −u

. The

relation between x and f can be obtained and shown as hysteresis curves in Figure

2.6.