Du C., Xie L. Modeling and Control of Vibration in Mechanical Systems

Подождите немного. Документ загружается.

4 Modeling and Control of Vibration in Mechanical Systems

FIGURE 1.3

Zoomed-in view of the hexapod.

actively increase the str uctural damping of ﬂexible systems at tached t o it.

Figur e 1.3 shows the zoomed-in view of the inside of the hexapod, revealing th e

arrangement of the six collo cated sensor-actuator legs. The wires shown in Figure

1.2 are the outp uts of the for ce sensors (each for one sensor) and inputs to the piezo-

electric actuato rs (each for one actuator), respectively.

Each of the legs i n the Stewart p latform consists of a PZT force sensor and an

ampliﬁed PZT actuator. They form a collocated sensor-actuator pair conﬁguration.

If an actuator and a sensor are collocated, the associated signals for the actuator

and sensor are power conjugated, i.e., the product of the actuated velocity and the

measured force represents the power that is extracted from the mechanical structure.

A collocated actuator-sensor pair thus enables the control of power that is supplied

to the mechanical structure. Collocated actuator-sensor pairs are suitable in active

vibration control applications in the sense that they guarantee damping and stability

robustness if design ed properly [33].

In this book, the modeling and v ibration controls for the magnetic recording sys-

tem and the Stewart platform will be detailed.

1.3 Vibration sources an d descriptions

Any oscillatory motion of bodies that repeatedly appears is called vibration or os-

cillation. There are usually forces associated with vibrations. They can be induced

by various types of excitation. Some of them are: ﬂuid ﬂow; rotating unbalanced

machi nery; str ucture ﬂexible modes; electrical torque; reciprocating machinery; mo-

tion induced in vehicles traveling over u neven surfaces; and ground motion caused

by earthquakes.

Flow induced vibration is generated by the forces exerted on an object by ﬂuid

motion. Such situati ons can be complicated by the fact that the motion of the vibrat-

Mechanical Systems and Vibration 5

ing object can alter the ﬂuid ﬂow conditions, thus changing the ﬂuid forces. Another

complicating factor is the mass of the ﬂuid, which increases the effective mass of the

system. Examples of vib ration caused b y ﬂui d motion inclu de: wave action on struc-

ture; vortex-induced vibration such as vibration of transmission cables, underwater

cables used for towing and str uctural sup port, and cooling towers and chimneys; vi-

bration caused by internal ﬂows, such as air ﬂow in hard d isk drives, ﬂow through

pipes and hoses having bends; structural vibration caused by ﬂuctuating aerodynamic

forces such as t urbulence [ 1][56]. In certain si tuations, the steady-state excitation

force due to ﬂuid motion is sinu soidal with an amplitude proportional to the square

of the forcing frequency. A model of the system u ndergoing such excitation is

m¨x + c ˙x + kx = F

sinωt, (1.1)

where m is the system mass, x is the system response, ω is the forcing frequency, k

and c are respectively stiffness and damping, and F

is the fo rce coefﬁcient. Furth er

analysis of system response to ﬂow ﬂuid motion is qu ite complicated and requires

detailed consi deration of ﬂuid mechani cs of the system.

Some oscillatory systems have simple harmonic motion of the form

y(t) = Bsin(ωt) + Ccos(ωt), (1.2)

where y(t) is the displacement of a mass, and is equ ivalent to

y(t) = Asin(ωt + φ), (1.3)

A =

+ C

, (1.4)

cos(φ) =

, sin(φ) =

. (1.5)

There occur some oscillations having exponential amplitude as follows:

y(t) = Ae

sin(ωt + φ), (1.6)

where oscil lation amplitude decays exponentially when r < 0, and grows i ndeﬁ-

nitely when r > 0.

Many types of motion cannot be easily represented by simple functions because

they are essential ly random. Examples include air turbulence to arm and suspension

in hard disk drives, ground motion due to an earthquake, and base motion that occurs

when a vehi cl e travels over an u neven surface. It is possible, however, to characterize

them by means of statistical averages and spectrum plots, in which Fourier analysis

is used to identify the major frequency components in the v ibration and they will be

described in more detail in the later part of the chapter.

1.4 Types of vibration

There are several ways to categorize vibrations. Basically, they can be calssiﬁed as

follows.

6 Modeling and Control of Vibration in Mechanical Systems

1.4.1 Free and forced vibration

If a system vibrates on its own aft er an i nitial di sturbance and no ext ernal force acts

on it, the ensuing vibration is known as f ree vibration. A direct example of free

vibration is the oscillation of a simple pendulum.

If a system vibration is due to an external force, the arising vibratio n is k nown as

forced vib ration. The oscillation in machines such as diesel engines that results from

an external force is an example of forced vibration. If the f requency of the external

force coin ci des with one of the natur al f requencies of the system, the p henomenon

known as resonance occurs, and the system undergoes oscillation. The occurrence of

that resonance causing large oscillation may lead to failu res of some str uctures such

as buildings, bridges, turbines, and airplane wings.

1.4.2 Damped a nd undamped vibration

If durin g oscillation there is no energy lost or dissipated in friction or other resistance,

the vibration is known as undamped vibration. On the other hand, if there is energy

lost during oscillation, it is called damped vibration. When analyzing vibration near

resonance in physical systems, consideration of damping becomes extremely impor-

tant.

1.4.3 Linear and nonlinear vibration

If all the b asic components in a vibratory system such as sprin g, mass and damper

behave linearly, the resulting vibr at ion is classiﬁed as linear vibration. On the o ther

hand, if any of the basic components behaves nonlin early, the vibration is categorized

as nonlinear vibration. Linear and nonlinear differential equations are used to govern

the behaviors of lin ear and n onlinear vibratory systems, respectively. If a vibration is

linear, the principle of linear systems such as superpositio n holds, and there are well

developed mathematical tool s for analysis. As for nonlinear vibration, the superposi-

tion principle is n ot valid, and techniques of analysis are more complicated and less

well known. Since all vibratory systems tend to behave nonlinearly with respect to

amplitude level o f oscillation, some knowledge of nonlinear vibration is desirable in

dealing with practical vibratory systems. A s is known, a d escribing function is one

approximation metho d used to analyze nonlinear vibratory systems.

1.4.4 Deterministic and random vibration

A vibration is known as det erministic vibration if it results from an excitation with

value or amplitude known at any given time. In some cases, the excitation acting on

a vibratory system is nondeterministic or random, and the value of the excitation at

a given time cannot be predicted. In these cases, a large amount of excitation dat a

collected may exhibit some statist ical regularity. Statistical methods can be used for

analysis, as it is possible to estimate averages such as the mean and vari ance values

of the random excitation. Examples of random excitations are air ﬂow inside hard

Mechanical Systems and Vibration 7

disk drives, road roughness and gro und motion during earthquakes. If the excitation

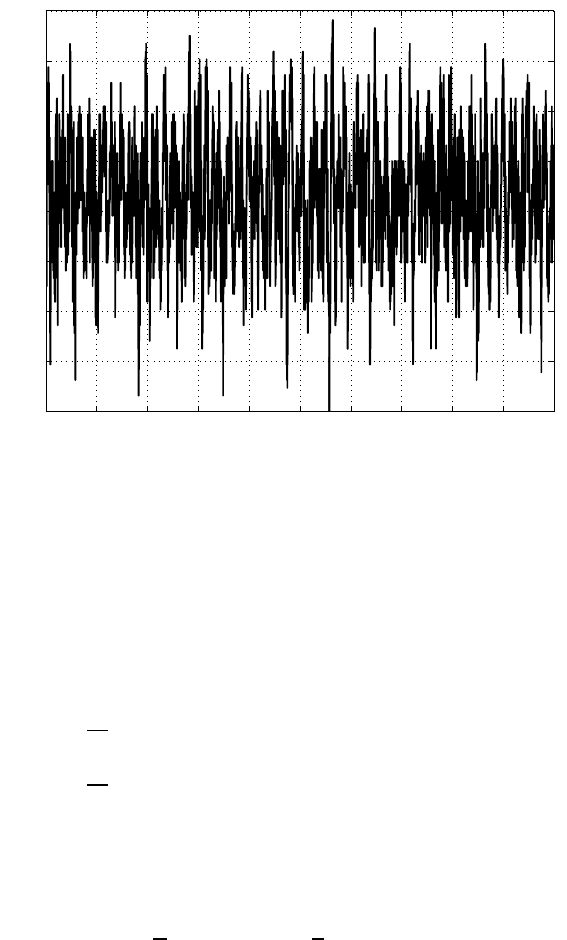
is random, the induced vibration is called random vibration, such as that shown in

Figur e 1.4. It can be described in terms of statistical quantities.

0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

0.8

Time(sec)

Vibration signal

FIGURE 1.4

An example of rando m vibration.

1.4.5 Periodic and nonperiodic vibration

Periodi c vibrati on can be represented by Fourier series as superposition of harmonic

components of vari ous frequencies. That is, i f x(t) is a periodic fu nction with period

τ, its Fourier series representation is given by

x(t) =

+ a

cos(ωt) + a

cos(2ωt) + ··· + b

sin(ωt) + b

sin(2ωt) + ...

∞

n=1

cos(nωt) + b

sin(nωt)), (1.7)

where ω = 2 π/τ is the fundamental frequency, and a

, a

, b

are constant coefﬁ-

cients given by

2π /ω

x(t)dt =

x(t)dt, (1.8)

8 Modeling and Control of Vibration in Mechanical Systems

2π /ω

x(t)cos(nωt)dt =

x(t)cos(nωt)dt, (1.9)

2π /ω

x(t)sin(nωt)dt =

x(t)sin(nωt)dt. (1.10 )

Let

, (1.11 )

= (a

+ b

)

1/2

. (1.12 )

The root mean square (RMS) value of the periodic function x(t) can be determined

RM S(x(t)) =

∞

n=0

. (1.13 )

Thus the mean sq uare value of x (t) is given by the sum of the squares of the absolute

values of the Fourier coefﬁcients. Equation (1.13) is known as Parseval’s formula for

periodic functio ns.

Although the series in (1.7) is an inﬁnite sum, most periodic functions can be

approximated by only a few harmonic functions.

A nonperiodic v ibration x(t) can be represented by the integral Fourier transform

pair:

x(t) =

2π

∞

−∞

X(ω)e

iωt

dω (1.14)

and

X(ω) =

∞

−∞

x(t)e

−iωt

dt. (1.15 )

The RMS value of the nonperiodic funct ion x(t) can be determined as

RM S(x(t)) =

∞

−∞

|X(ω)|

2πτ

dω. (1.16 )

Equation (1.16) is known as Parseval’s formula for nonperiodic functions.

1.4.6 Broad-band and narrow-band vibration

A broad-band vibration is a stationary random process whose spectral density func-

tion has signiﬁcant values over a range or band of frequencies which is appr oximately

of the same order of magnitude as the center frequency of the band. The density in

Mechanical Systems and Vibration 9

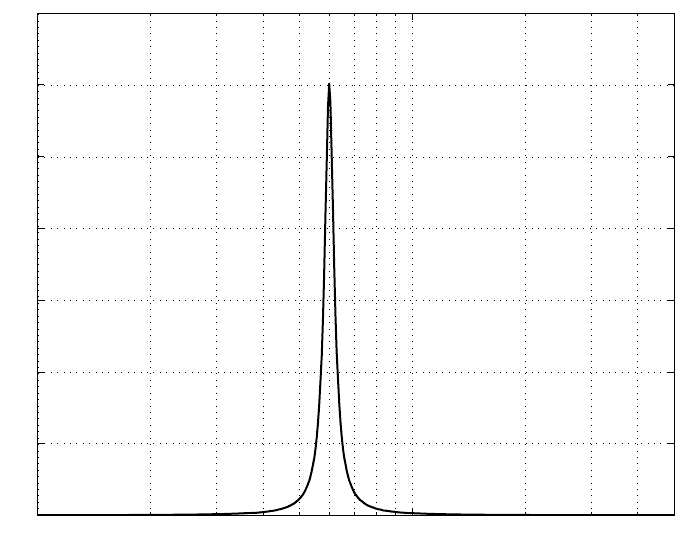
Figur e 1.5 describes a broad-b and vibration, which is composed of components con-

taining frequencies over a wide or b road frequency range. A narrow-band rando m

vibration is a st ationary vibr at ion whose spectral density function has signiﬁcant val-

ues only in a range o f frequency whose width is small compared to the magnitude

of the center frequency. Figure 1.6 shows a vibration containing frequencies over a

narrow band.

Frequency(Hz)

Magnitude(dB)

FIGURE 1.5

Spectrum density of broad-band vibration .

A random process whose power spectral density is constant over a frequency range

is called w hite noise. It is called ideal white noise if t he band of frequ encies is

inﬁnitely wide. An ideal white noise is physically unrealizable, since the variance of

such a rando m process would be inﬁn ite because the area under the spectrum would

be inﬁnite. It is called band-limited white noise if the band of frequencies has ﬁnite

cut-off frequencies ω

and ω

. The variance of a band-limited white noise is given

by the total area under the spectrum, namely, 2S

(ω

− ω

), where S

denotes the

constant value of the spectral density.

10 Modeling and Control of Vibration in Mechanical Systems

Frequency(Hz)

Magnitude(dB)

FIGURE 1.6

Spectrum density of narrow-band vibratio n.

Mechanical Systems and Vibration 11

1.5 Random v ibration

1.5.1 Random process

In contrast to deterministic excitations, in many applications the inputs are not well

known and can be described only in terms of statistical measures such as mean value,

variance and standard deviation .

Mean value

The average is called the mean or expected value, often represented by µ. For dis-

crete values, such as those pro duced by digital data acquisition , the mean is deﬁned

E(x) =

j=1

. (1.17 )

For a continuous function x(t), the mean is

E[x(T

)] =

x(t)dt (1.18 )

where the time duration of the data sample is T

Variance

Two signals may have the same mean value but one may ﬂuctuate with greater

amplitude about th e mean. So we also need a measure of the range of ﬂuctuation.

Simply specifyin g the minimum and maximum values is insufﬁcient because a single

large ﬂuct uation (above or b el ow the mean) can be misleading. A measure that

indicates the spread about the mean is the variance, which is deﬁned as t he average

value of the sq uare of the difference betw een the sig nal and its mean. The variance

is calculated for a discrete signal as follows.

var(x) = σ

j=1

−µ)

, (1.19 )

where σ

is the variance and σ is called the standa rd d eviation.

For a sig nal continuous in time, the variance is calculated fro m

var(x , T

) =

[x(t) − µ]

dt. (1.20)

The mean-square value of x is the expected value of x

and is deno ted E(x

). The

RMS value of x is

E(x

). The relation between the variance, the mean square,

and the mean is as follows.

= E(x

) − [E(x)]

. (1.21 )

12 Modeling and Control of Vibration in Mechanical Systems

If the mean of x is zero, the standard deviation σ

of x is calculated from

E(x

), (1.22)

and is thus the same as the RMS value.

A random input will generate a random response, and the output signal given by

its sensor will appear to be random. Random signals, like the example shown in

Figur e 1.4, have no apparent pattern and never repeat. Another characteristic of a

random signal is that it is impossi ble to predict what the signal will be in the fut ure,

even if we h ave the past values of the signal.

1.5.2 Stationary random process

A special case of a random process is one that is station ary, which means that its

statistical properties (such as its mean and variance) are time-independent.

If x(t) is stationary, its mean and covariance will b e independent of t:

E[x(t)] = E[x(t + τ )] = µ, (1.23)

and

E[x(t)x(t + τ )] = σ

(τ). (1.24)

1.5.3 Gaussian random process

A Gaussian or normal random process has a number of remarkable properties that

permit the computation of random vibration characteristics in a simple manner. The

probability density function of a Gaussian process x(t) is given by

p(x) =

√

2πσ

−

(

x−¯x

)

, (1 .25)

where ¯x and σ

denote the mean value and standard d eviation of x. The mean ¯x and

standard deviation σ

of x(t) vary with t for a nonstationary process but are con stants

for a stationary process. A very important property o f a Gaussian process is that the

form of its probability distri bution is invariant with respect to linear operations. This

means that if the excitation of a linear system is a Gaussian process, the steady-state

response is generall y a different random process, but still a normal one. The only

changes are that the magnitude of the mean and standard deviation of the response

are different from those of the excitation.

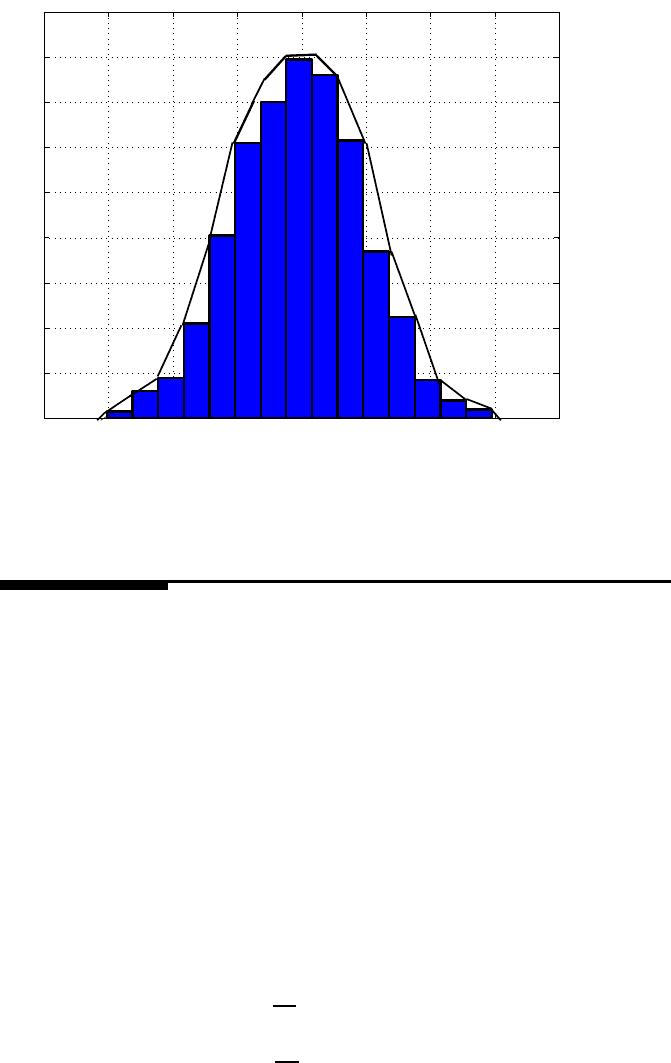
The graph of a Gaussian probability density function has a bell-shaped envelope

as seen in Fig ure 1.7, and i s symmetric about the mean value; its spread is governed

by t he value of the st and ard deviat ion.

Mechanical Systems and Vibration 13

−4 −3 −2 −1 0 1 2 3 4

100

120

140

160

180

Signal x

Probability density

FIGURE 1.7

Histo gram of signal x.

1.6 Vibration analysis

1.6.1 Fourier transform and spectrum analysis

We know that a periodic signal can be expressed as a Fourier series of h armonic

functions. The Fourier series coefﬁcients, when plotted versus fr equ ency, gives a

plot of the sp ectrum of the signal. The spectrum graphically di splays the frequency

content of the signal.

A nonperiodic function is expressed wi th the f ollowing Fourier transfor m p ai r:

x(t) =

∞

−∞

a(ω )cos(ωt)dω +

∞

−∞

b(ω)sin(ωt)dω, (1.26 )

where

a(ω ) =

2π

∞

−∞

x(t)cosωtdt, (1.27)

b(ω) =

2π

∞

−∞

x(t)sinωtdt. (1.28)