Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics
Подождите немного. Документ загружается.

836 Part D Scattering Theory
56.1 Rydberg Collision Processes
(A) State-Changing Collisions
Quasi-elastic -mixing collisions:
A
∗
(n) + B → A
∗
(n
) +B . (56.1)
Quasi-elastic J-mixing collisions: Fine structure
transitions with J =| ±1/2|→J
=| ±1/2| are
A
∗
(nJ) +B → A
∗
(nJ
) +B . (56.2)
Energy transfer n-changing collisions:
A
∗
(n) + B(β) → A
∗
(n
) +B(β
), (56.3)
where, if B is a molecule, the transition β → β
represents an inelastic energy transfer to the rotational-
vibrational degrees of freedom of the molecule B from
the Rydberg atom A
∗
.
Elastic scattering:
A
∗
(γ) +B → A
∗
(γ) +B , (56.4)
where the label γ denotes the set of quantum numbers
n,or n,,J used.
Depolarization collisions:
A
∗
(nm) +B → A
∗
(nm
) +B , (56.5a)
A
∗
(nJM ) + B → A
∗
(nJM
) +B . (56.5b)
(B) Ionizing Collisions
Direct and associative ionization:
A
∗
(γ) +B(β) →
A
+
+ B(β
) +e
−
BA
+
+ e
−
.
(56.6)
Penning ionization:
A
∗
(γ) +B → A+ B
+
+e
−
. (56.7)
Ion pair formation:
A
∗
(γ) +B → A
+
+ B
−
. (56.8)
Dissociative attachment:
A
∗
(γ) +BC → A
+
B
−
+C . (56.9)
56.2 General Properties of Rydberg States
Table 56.1 displays the general n-dependence of a num-
ber of key properties of Rydberg states and some specific
representative values for hydrogen.
56.2.1 Dipole Moments
Definition. D
i→ f
=−eX
i→ f
where
X
i→ f
=φ
f
|
j
e
ik·r
j
r
j
|φ
i
. (56.10)
Hydrogenic Dipole Moments. See Bethe and
Salpeter [56.1] and the references by Khandelwal and
co-workers [56.2–5] for details and tables.
Exact Expressions. In the limit |k|→0, the dipole al-
lowed transitions summed over final states are
X
1s→n
2
=
2
8
3
n
7
(n−1)
2n−5
(n+1)
2n+5
, (56.11a)
X
2s→n
2
=
2
5
3n
3
1
2
−1n
2n−7
1
2
+1n
2n+7
1
4
−
1
n
2
1−
1
n
2
,
(56.11b)
X
2 p→n
2
=
2
5
144
1
n
3
1
2
−
1
n
2n−7
1
2
+
1
n
2n+7
11 −
12
n
2
.
(56.11c)
Asymptotic Expressions. For n 1,
n
3
X
1s→n
2
≈ 1.563 +
5.731
n
2
+
13.163
n
4
+
24.295
n
6
+
39.426
n
8
+
58.808
n
10
, (56.12a)
n
3
X
2s→n
2
≈ 14.658 +
180.785
n
2
+
1435.854
n
4
+
9341.634
n
6
+
54 208.306
n
8
+
292 202.232
n
10
, (56.12b)
n
3
X
2 p→n
2
≈ 13.437 +
218.245
n
2
+
2172.891
n
4
+
17 118.786
n
6
+
117 251.682
n
8
+
731427.003
n
10
. (56.12c)
Part D 56.2

Rydberg Collisions: Binary Encounter, Born and Impulse Approximations 56.2 General Properties of Rydberg States 837
Table 56.1 General n-dependence of characteristic properties of Rydberg states. After [56.6]
Property n−dependence n= 10 n = 100 n = 500 n = 1000
Radius (cm) n
2
a
0
/Z 5.3×10
−7
5.3×10
−5
1.3×10
−3
5.3×10
−3
Velocity (cm/s) v
B
Z/n 2.18 × 10
7
2.18 × 10
6
4.4×10
5
2.18 × 10
5
Area (cm
2
) πa
2
0
n
4
/Z
2
8.8×10
−13
8.8×10
−9
5.5×10
−6
8.8×10
−5
Ionization potential (eV) Z
2
R
∞
/n
2
1.36 × 10
−1
1.36 × 10
−3
5.44 × 10
−5
1.36 × 10
−6
Radiative lifetime (s)
a
n
5
(3lnn −
1
4
)/(A
0
Z
4
) 8.4×10
−5
17 7.3×10
4
7.22 hours
Period of classical motion (s) 2π/ω
n,n±1
= hn
3
/(2Z
2
R
∞
) 1.5×10
−13
1.5×10
−10
1.9×10
−8
1.5×10
−7
Transition frequency (s
−1
) ω
n,n±1
= 2Z
2
R
∞
/( n
3
) 4.1×10
13
4.1×10
10
3.3×10
8
4.1×10
7
Wavelength (cm) λ
n,n±1
= 2πc/ω
n,n±1
4.6×10
−3
4.6 570 4.5609 × 10
3
a
A
0
=
8α
3
/(3
√
3π)
(v
B
/a
0
)
56.2.2 Radial Integrals
Definition.
R
n
n
≡
∞
0
R
n
(r)rR
n
(r)r
2
dr , (56.13)
where R
n
(r) are solutions to the radial Schrödinger
equation. See Chapt. 9 for specific representations of
R
n
for hydrogen.
Exact Results for Hydrogen. For
= −1andn =
n
[56.7],
R
n
−1
n
=
a
0
Z
(−1)
n
−
(4nn
)
+1
(n−n
)
n+n
−2−2
4(2 −1)!(n +n
)
n+n
×
(n+)!(n
+ −1)!
(n
+
)!(n− −1)!
1/2
×
2
F
1
(−n+ +1, −n
+;2;Y)
−
n−n
n+n
2
2
F
1
(−n+−1, −n
+;2;Y)
,
(56.14)
where Y =−4nn
/(n −n
)
2
.Forn =n
,
R
n−1
n
=
a
0
Z
3
2
n
n
2
−
2
. (56.15)
Semiclassical Quantum Defect Representation [56.8].
R
n
n
2
=
a
0
Z
2
n
2
c
2∆
1 −
∆
>
n
c
J
∆−1
(−x)
−
1 +
∆
>
n
c
J
∆+1
(−x)
+
2
π
sin(π∆)(1 −e)
2
, (56.16)
where
n
c
= 2n
∗
n
∗
/(n
∗
+n
∗
), (56.17a)
∆ = n
∗
−n
∗
, (56.17b)
∆ =
−,
>
= max(,
), (56.17c)
x = e∆, e =
1 −(
>
/n
c
)
2
, (56.17d)
and J
n
(y) is the Anger function.
The energies of the states n and n
are given in
terms of the quantum defects by
E
n
=−Z
2
R
∞
/n
∗2
, n
∗
= n−δ
, (56.18a)
E
n
=−Z
2
R
∞
/n
∗2
, n
∗
= n
−δ
. (56.18b)
Sum Rule. For hydrogen
n
R
n
−1
n
2
=
n
R
n
+1
n
2
(56.19a)
=
n
2
a
2
0
2 Z
2
5n
2
+1 −3( +1)
.
(56.19b)
See §61 of [56.1] for additional sum rules.
56.2.3 Line Strengths
Definition.
S(n
, n) = e
2
(2 +1)
r
n
,n
2
(56.20a)
= e
2
max(,
)
R
n
n
2
, (56.20b)
where
= ±1. For hydrogen
S(n
, n) = 32
ea
0
Z
2
(nn
)
6
(n−n
)
2(n+n
)−3
(n+n
)
2(n+n
)+4
×
2
F
1
(−n
, −n +1;1;Y)
2
−
2
F
1
(−n
+1, −n;1;Y)
2
,
(56.21)
where Y =−4nn
/(n −n
)
2
.
Part D 56.2
838 Part D Scattering Theory
Semiclassical Representation [56.9].
S(n
, n) =
32
π
√
3
ea
0
Z
2
(εε
)
3/2
(ε −ε
)
4
G(∆n), (56.22)
where ε = 1/n
2
, ε
=1/n
2
, and the Gaunt factor G(∆n)
is given by
G(∆n) = π
√
3
∆n
J
∆n
(∆n)J
∆n
(∆n), (56.23)
where the prime on the Anger function denotes differ-
entiation with respect to the argument ∆n. Equation
(56.23) can be approximated to within 2% by the
expression
1 −
1
4|∆n|
.
(56.24)
Relation to Oscillator Strength.
S(n
, n) =
,
S(n
, n)
= 3e
2
a
2
0
R
∞
ω
,
f
n
,n
. (56.25)
Connection with Radial Integral.
− f
n
,n
=
ω
3R
∞
max(,
)
(2 +1)
R
n
n
.
(56.26)
Density of Line Strengths. For bound-free n → E
transitions in a Coulomb field, the semiclassical repre-
sentation [56.6]is
d
dE
S(n, E) = 2n(2 +1)
R
∞
ω
2
×
J
∆
(e∆)
2
+
1 −
1
e
2
J
∆
(e∆)
2
e
2
a
2
0
R
∞
,
(56.27)
where ∆ = ωn
3
/2R
∞
and e =
1 −
+
1
2
2
/n
2
.
Asymptotic expression for ∆ 1:
d
dE
S(n, E) =
2(2 +1)
3π
2
R
∞
ω
2
+
1
2
4
n
3
×
K
2
1/3
(η) +K
2
2/3
(η)
e
2
a
2
0
R
∞
,
(56.28)
where η = (E/R
∞
)( +1/2)
3
/6andtheK
ν
(x) are
Bessel functions of the third kind.
Line Strength of Line n.
S
n
≡ S(n) =
k=0
S(n+k, n)
1
k
3
. (56.29)
Born Approximation to Line Strength S
n
[56.6].
S
B
n
=
Z
2
R
∞
E
1
2
ln(1 +ε
e
/ε)
k=0
1 −
1
4k
1
k
4
+
4
3
ε
e
ε +ε
e
k=0
1 −
0.60
k
1
k
3
=
Z
2
R
∞
E
0.82 ln
1 +
ε
e
ε
+
1.47ε
e
ε +ε
e
, (56.30)
where ε =|E
n
|Z
2
/R
∞
and ε
e
= ε/Z
2
R
∞
.
56.2.4 Form Factors
F
n
n
(Q) =
,m
,m
nm
e
iQ·r
n
m
2
. (56.31)
Connection with Generalized Oscillator Strengths.
f
n
n
(Q) =
Z
2
∆E
n
2
Q
2
a
2
0
F
n
n
(Q). (56.32)
Semiclassical Limit.
lim
Q→0
f
n
n
(Q) =
32
3n
2
nn
∆n(n +n
)
3
× ∆nJ
∆n
(∆n)J
∆n
(∆n), (56.33)
where J
m
(y) denotes the Bessel function.
Representation as Microcanonical Distribution.
F
n
,n
(Q) =(2 +1)
2Z
2
R
∞
n
3
dp|g
n
( p)|
2
× δ
( p−
Q)
2
2m
−
p
2
2m
−E
n
−E
n
,
(56.34)
F
n
,n
(Q) =
4Z
2
R
∞
2
(nn
)
3
dp dr
(2π )
3
δ
p
2
2m
−
Ze
2
r
−E
n
× δ
( p−
Q)
2
2m
−
Ze
2
r
−E
n
,
(56.35)
=
2
9
3π(nn
)
3
κ
5
(κ
2
+κ
2
+
)
3
(κ
2
+κ
2
−
)
3
,
(56.36)
where κ = Qa
0
/Z and κ
±
=|1/n±1/n
|.
Part D 56.2
Rydberg Collisions: Binary Encounter, Born and Impulse Approximations 56.3 Correspondence Principles 839
56.2.5 Impact Broadening
The total broadening cross section of a level n is
σ
n
=
πa
2
0
/Z
4
n
4
S
n
. (56.37)
The width of a line n → n +k is [56.10]
γ
n,n+k
= n
e
vσ
n
+vσ
n+k
, (56.38)
where n
e
is the number density of electrons, and
vσ
n
=
k=0
vσ
n+k,n
=
n
4
Z
3
K
n
(56.39a)
=
n
4
πa
2
0
v
B
Z
3
θ
3/2
∞
0
e
−E/k
B
T
S
n
E dE
(Z
2
R
∞
)
2
,
(56.39b)
where θ = k
B
T/Z
2
R
∞
. See Chapt. 59 for collisional line
broadening.
56.3 Correspondence Principles
Correspondence principles are used to connect quantum
mechanical observables with the corresponding classical
quantities in the limit of large n. See [56.11] for details
on the equations in this section.
56.3.1 Bohr–Sommerfeld Quantization
A
i
= J
i
∆w
i
p
i
dq
i
= 2π (n
i
+α
i
), (56.40)
where n
i
= 0, 1, 2,... and α
i
= 0 if the generalized
coordinate q
i
represents rotation, and α
i
=1/2ifq
i
rep-
resents a libration.
56.3.2 Bohr Correspondence Principle
E
n+s
−E
n
= hν
n+s,n
∼ s ω
n
, s =1, 2,... n ,
(56.41)
where ν
n+s,n
is the line emission frequency and ω
n
is
the angular frequency of classical orbital motion. The
number of states with quantum numbers in the range
∆n is
∆N =
D
i=1
∆n =
D
i=1
(
∆J
i
∆w
i
)
/(2π
)
D
=
D
i=1
(∆ p
i
∆q
i
)/(2π )
D
, (56.42)
for systems with D degrees of freedom, and the mean
value
¯
F of a physical quantity F(q) in the quantum
state Ψ is
¯
F =Ψ |F(q)|Ψ =
n,m
a
∗
m
a
n
F
(q)
mn
e
iω
mn
t
, (56.43)
where the F
(q)
mn
are the quantal matrix elements between
time independent states.
The first order S-matrix is
S
fi
=−
iω
2π
∞
−∞
dt
2π/ω
0
V[R(t), r(t
1
)]e
isω(t
1
−t)
dt
1
,
(56.44)
where R denotes the classical path of the projectile and
r the orbital of the Rydberg electron.
56.3.3 Heisenberg Correspondence
Principle
For one degree of freedom [56.11],
F
(q)
mn
(R) =
∞
0
φ
∗
m
(r)F(r, R)φ
n
(r) dr (56.45)
=
ω
2π
2π/ω
0
F
(c)
r(t)
e
isωt
dt . (56.46)
The three-dimensional generalization is [56.11]
F
(q)
n,n
∼ F
(c)
s
(J) =
1
8π
3
F
c
r(J, w)
e
is·w
dw ,
(56.47)
where n, n
denotes the triple of quantum numbers
(n,,m), (n
,
, m
), respectively, and s = n−n
.
The correspondence between the three dimensional
quantal and classical matrix elements in (56.47) follows
from the general Fourier expansion for any classical
function F
(c)
(r) periodic in r,
F
(c)
r(t)
=
s
F
(c)
s
(J) exp(−is· w), (56.48)
where J, w denotes the action-angle conjugate vari-
ables for the motion. For the three dimensional Coulomb
Part D 56.3
840 Part D Scattering Theory
problem, the action-angle variables are
J
n
= n ,w
n
=
∂E
∂J
n
t +δ,
J
=
+
1
2
,w
= ψ
E
,
J
m
= m ,w
m
= φ
E
, (56.49)
where ψ
E
is the Euler angle between the line of nodes
and a direction in the plane of the orbit (usually taken
to be the direction of the perihelion or perigee), and is
constant for a Coulomb potential. The Euler angle φ
E
is
the angle between the line of nodes and the fixed x-axis.
See [56.11] for details.
The first order S-matrix is
S
fi
=−
iω
2π
2π/ω
0
dt
e
∞
−∞
dtV
R(t), r(t +t
e
)
e
isωt
e
,
(56.50)
with s = i − f , R is the classical path of the projectile,
and r(t
e
) is the classical internal motion of the Rydberg
electron.
56.3.4 Strong Coupling Correspondence
Principle
The S-matrix is
S
fi
=
ω
2π
2π/ω
0
dt
e
exp
!
i(sωt
e
)
−
i
∞
−∞
V
R(t), r(t +t
e
)
dt
"
. (56.51)
See [56.11–14] for additional details.
56.3.5 Equivalent Oscillator Theorem
n
a
n
(t)V
fn
(t)e
iω
fn
t
=
d=− f
a
d+ f
(t)V
d
(t)e
−idωt
.
(56.52)
The S-matrix is
S
n
,n
= a
n
(t →∞) (56.53)
=
2π
0
dw
8π
3
exp
is· w −
i
∞
−∞
V(w +ωt, t) dt
.
56.4 Distribution Functions
The function W
α
(x)dx characterizes the probability
(distribution) of finding an electron in a Rydberg or-
bital α within a volume dx centered at the point x in
phase space. Integration of the distribution function W
α
over all phase space v olumes dx yields, depending upon
the normalization chosen, either unity or the density of
states appropriate to the orbital α.
56.4.1 Spatial Distributions
Distribution over n,,m [56.6]:
W
nm
(r,θ)r
2
sin θ drdθ (56.54)
=
r
2
sin θ dr dθ
π
2
a
2
r
e
2
−(1 −r/a)
2
sin
2
θ −(m/)
2
1/2
,
where a = Ze
2
/2|E|=n
2 2
/mZe
2 2
is the semimajor
axis, and e
2
= 1 −(/n)
2
is the eccentricity.
Distribution over n,:
W
n
(r,θ)r
2
sin θ drdθ
= g(n)
r
2
sin θ drdθ
2πa
2
r
e
2
−(1 −r/a)
2
1/2
, (56.55)
where g(n) = 2.
Distribution over n:
W
n
(r)r
2
dr = g(n)
2
π
1 −
1 −
r
a
2
1/2
r dr
a
2
,
(56.56)
with g(n) = n
2
.
56.4.2 Momentum Distributions
Distribution over n,[56.6]:
W
n
( p) p
2
dp = g(n)
4
π
dx
1 +x
2
2
, (56.57)
where x = p/ p
n
and p
2
n
= 2m|E|.
Distribution over n:
W
n
( p) p
2
dp = g(n)
32
π
x
2
dx
1 +x
2
4
. (56.58)
Sum Rules.
1
n
2
,m
G
nm
(k)
2
=
na
0
Z
3
8
π
2
x
2
+1
4
,
(56.59a)
Part D 56.4
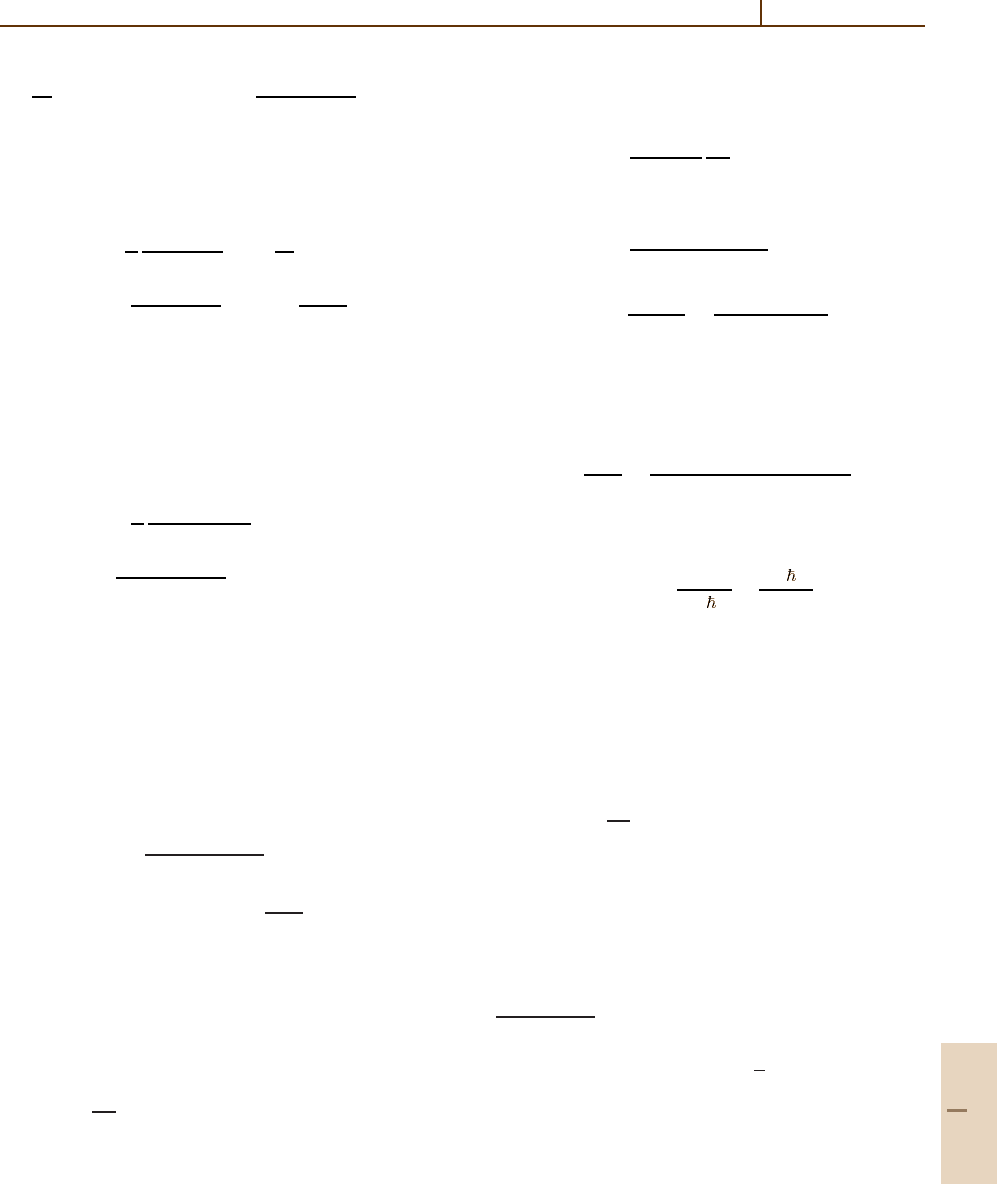
Rydberg Collisions: Binary Encounter, Born and Impulse Approximations 56.5 Classical Theory 841
1
n
2
n−1
=0
(2 +1)
g
n
(k)
2
k
2
=
32na
0
x
2
πZ
x
2
+1
4
,
(56.59b)
where x = nka
0
/Z,and
G
nm
(k) =g
n
(k)Y
m
(
ˆ
k), (56.60a)
g
n
(k) =
2
π
(n−−1)!
(n+)!
1/2
a
0
Z
3/2
2
2(+1)
n
2
!
×
(−ix)
x
2
+1
+2
C
(+1)
n−−1
x
2
−1
x
2
+1
,
(56.60b)
where C
( j)
i
(y) is the associated Gegenbauer polynomial.
See Chapt. 9 for additional details on hydrogenic wave
functions.
Quantum Defect Representation [56.15].
g
n
(k) =−
2
π
Γ(n
∗
−1)
Γ(n
∗
++1)
1/2
n
∗
(a
0
/Z)
3/2
2
2(+1)
×
( +1)!(−ix)
x
2
+1
+2
J(n
∗
,+1; X),
(56.61)
where n
∗
= n−δ, δ being the quantum defect, and
x = n
∗
ka
0
/Z. The function J is given by the recurrence
relation
J(n
∗
,+1; X) =−
1
2(2 +2)
∂
∂X
J(n
∗
,; X),
(56.62)
J(n
∗
, 0; X) =−
n
∗
sin
n
∗
(β −π)
sin(β −π)
−
sin n
∗
π
π
1
0
1 −s
2
s
n
∗
1 −2Xs +s
2
ds ,
(56.63)
where X =
x
2
−1
/
x
2
+1
,andβ =cos
−1
X.Inthe
limit n
∗
,(56.61) becomes
|g
n
(k)|
2
=4
n
∗
a
0
Z
3
1−(−1)
cos
2n
∗
(β −π)
πx
2
(x
2
+1)
2
.
(56.64)
Classical Density of States.
ρ(E) =
δ
[
E − H(p, r)
]
dpdr
(2π )
3
=
n
5 2
mZ
2
e
4
.
(56.65)
56.5 Classical Theory
The classical cross section for energy transfer ∆E be-
tween two particles, with arbitrary masses m
1
, m
2
and
charges Z
1
, Z
2
, is given by [56.16]
σ
∆E
(v
1
, v
2
) =
2π(Z
1
Z
2
e
2
V)
2
v
2
∆E
3
(56.66)
×
1 +cos
2
¯
θ +
∆E
µvV
cos
¯
θ
,
valid for −1 ≤cos
¯
θ −∆E/(µvV ) ≤1, and σ
∆E
(v
1
, v
2
)
= 0otherwise,where
v = v
1
−v
2
, (56.67a)
V = (m
1
v
1
+m
2
v
2
)/M , (56.67b)
cos
¯
θ =
1
vV
v · V ,
(56.67c)
and µ = m
1
m
2
/M, M = m
1
+m
2
. If particle 2 has an
isotropic velocity distribution in the lab frame, the ef-
fective cross section averaged over the direction
ˆ
n
2
of v
2
is
v
1
σ
(eff)
∆E
(v
1
, v
2
) =
1
4π
d
ˆ
n
2
|v
1
−v
2
ˆ
n
2
|σ
∆E
(v
1
, v
2
).
(56.68)
If v
1
is also isotropic, then the average of (56.68),
together with (56.66), gives for the special case of
a Coulomb potential
σ
(eff)
∆E
(v
1
, v
2
)
=
π
Z
1
Z
2
e
2
2
4|∆E|3v
2
1
v
2
v
2
1
−v
2
2
v
2
2
−v
2
1
v
−1
l
−v
−1
u
+
v
2
1
+v
2
2
+v
2
1
+v
2
2
(v
u
−v
) −
1
3
v
3
u
−v
3
l
,
(56.69)
where
v
1
=
v
2
1
−2∆E/m
1
1/2
, (56.70)
Part D 56.5

842 Part D Scattering Theory
v
2
=
v
2
2
+2∆E/m
2
1/2
, (56.71)
and v
u
, v
l
are defined below for cases 1.–4. With the
definitions
∆ε
12
= 4m
1
m
2
(E
1
−E
2
)/M
2
, ∆m
12
=|m
1
−m
2
| ,
∆
˜
ε
12
=
4m
1
m
2
M
2
E
1
v
2
v
1
−E
2
v
1
v
2
,
the four cases are
1. ∆E ≥ ∆ε
12
+|∆
˜
ε
12
|≥0, and 2m
2
v
2
≥ ∆m
12
v
1
:
v
l
= v
2
−v
1
,v
u
= v
1
+v
2
, ∆E ≥ 0 ;
(56.72a)
v
l
= v
2
−v
1
,v
u
= v
1
+v
2
, ∆E ≤ 0 .
(56.72b)
If 2m
2
v
2
< ∆m
12
v
1
,thenσ
eff
∆E
(v
1
,v
2
) = 0,
2. ∆ε
12
−∆
˜
ε
12
≤ ∆E ≤ ∆ε
12
+∆
˜
ε
12
,andm
1
> m
2
:
v
l
= v
2
−v
1
,v
u
= v
1
+v
2
, ∆E ≥ 0 ;
(56.72c)
v
l
= v
2
−v
1
,v
u
= v
1
+v
2
, ∆E ≤ 0
(56.72d)
3. ∆E ≤ ∆ε
12
−|∆
˜
ε
12
|≤0, and 2m
1
v
1
≥ ∆m
12
v
2
:
v
l
= v
1
−v
2
,v
u
= v
1
+v
2
, ∆E ≥ 0 ;
(56.72e)
v
l
= v
1
−v
2
,v
u
= v
1
+v
2
, ∆E ≤ 0 .
(56.72f)
If 2m
1
v
1
< ∆m
12
v
2
,thenσ
eff
∆E
(v
1
,v
2
) = 0,
4. ∆ε
12
+∆
˜
ε
12
≤ ∆E ≤ ∆ε
12
−∆
˜
ε
12
,andm
1
< m
2
:
v
l
= v
1
−v
2
,v
u
= v
1
+v
2
, ∆E ≥ 0 ;
(56.72g)
v
l
= v
1
−v
2
,v
u
= v
1
+v
2
, ∆E ≤ 0 .
(56.72h)
If 2m
1
v
1
< ∆m
12
v
2
,thenσ
eff
∆E
(v
1
,v
2
) = 0.
Since v
1
and v
2
,givenby(56.70)and(56.71) respec-
tively, must be real, σ
∆E
(v
1
, v
2
) =0for∆E outside the
range
−
1
2
m
2
v
2
2
≤ ∆E ≤
1
2
m
1
v
2
1
, (56.73)
which simply expresses the fact that the particle losing
energy in the collision cannot lose more than its initial
kinetic energy.
The cross section (56.69) must be integrated over
the classically allowed range of energy transfer ∆E
and averaged over a prescribed speed distribution
W(v
2
) before comparison with experiment can be made.
See [56.16,17] for details.
Classical Removal Cross Section [56.18]. The cross
section for removal of an electron from a shell is given by
σ
r
(V) =
∞
0
f(v)σ
∆E
(v
1
, v
2
)dv. (56.74)
Total Removal Cross Section [56.18]. In an independent
electron model,
σ
total
r
(V) = N
shell
σ
r
(V), (56.75)
where N
shell
is the number of equivalent electrons in
a shell. In a shielding model,
σ
total
r
(V) =
1 −
(N
shell
−1)
4π
¯
r
2
σ
r
(V)
N
shell
σ
r
(V),
(56.76)
where
¯
r
2
is the root mean square distance between elec-
trons within a shell. Experiment [56.19]favors(56.76)
over (56.75). See Fig. 4a–e of [56.18] for details.
Classical trajectory and Monte-Carlo methods are
covered in Chapt. 58.
56.6 Working Formulae for Rydberg Collisions
56.6.1 Inelastic n,-Changing Transitions
A
∗
(n) + B → A
∗
(n
) +B+∆E
n
,n
, (56.77)
where ∆E
n
,n
= E
n
−E
n
is the energy defect. The
cross section for (56.77) in the quasifree electron
model [56.20]is
σ
n
,n
(V) =
2πa
2
s
V/v
B
2
n
3
f
n
,n
(λ) , n ,
(56.78)
where a
s
is the scattering length for e
−
+ B
scattering, λ = n
∗
a
0
ω
n
,n
/V, ω
n
,n
=|∆E
n
,n
|/ ,
Part D 56.6
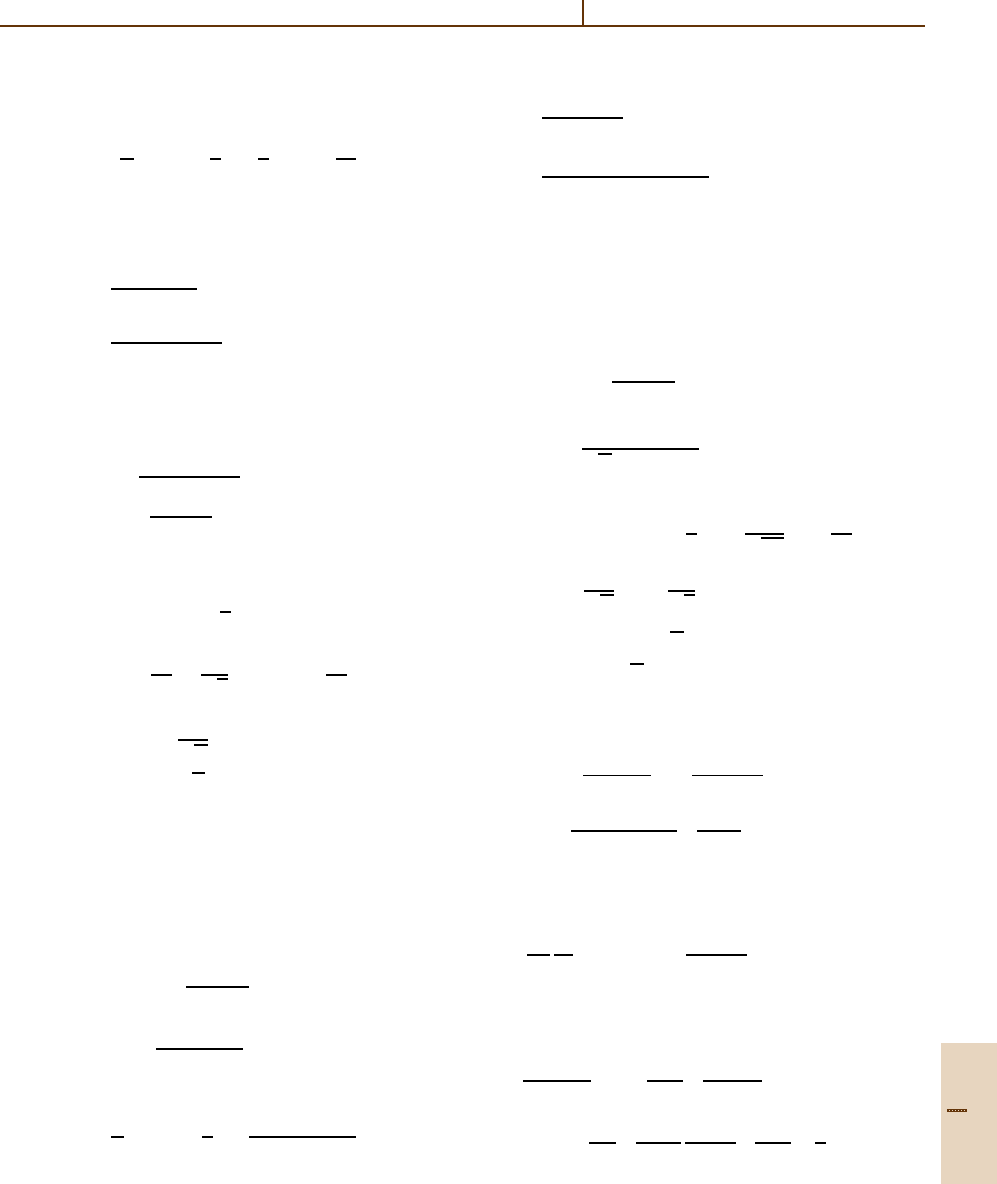
Rydberg Collisions: Binary Encounter, Born and Impulse Approximations 56.6 Working Formulae for Rydberg Collisions 843
E
n
=−R
∞
/n
2
,andE
n
=−R
∞
/n
∗2
, with
n
∗
= n−δ
.Also,v
B
is the atomic unit of velocity
(see Chapt. 1), and
f
n
,n
(λ) =
2
π
tan
−1
2
λ
−
λ
2
ln
1 +
4
λ
2
.
(56.79)
Limiting cases: f
n
,n
(λ) → 1asλ → 0, and f
n
,n
(λ) ∼
8/
3πλ
3
for λ 1. Then
σ
n
,n
∼
2πa
2
s
(V/v
B
)
2
n
3
,λ→ 0 ,
16a
2
s
Vn
3
3v
B
|δ
+∆n|
3
,λ 1 .
(56.80)
Rate Coefficients.
σ
n
,n
(V)≡Vσ
n
,n
(V)/V (56.81a)
=
2πa
2
s
V
T
/v
B
2
n
3
ϕ
n
,n
(λ
T
), (56.81b)
where V
T
=
√
2k
B
T/µ, λ
T
= n
∗
a
0
ω
n
,n
/V
T
,
∆n =n
−n,andµ is the reduced mass of A–B.The
function ϕ
n
,n
(λ
T
) in (56.81b)isgivenby
ϕ
n
,n
(λ
T
) = e
λ
2
T
/4
erfc
1
2
λ
T
(56.82a)
−
λ
T
π
∞
0
du
√
u
e
−u
ln
$
1 +
4
λ
2
T
%
=
1 −
λ
T
√
π
ln
1/λ
2
T
,λ
T
→ 0
2/
√
πλ
3
T
,λ
T
1
(56.82b)
and erfc (x) is the complementary error function.
56.6.2 Inelastic n → n
Transitions
A
∗
(n) + B → A
∗
(n
) +B+∆E
n
n
. (56.83)
(A) Cross Sections.
σ
n
n
=
(2 +1)
n
2
σ
n
,n
, (56.84)
σ
n
,n
(V) =
2πa
2
s
(V/v
B
)
2
n
3
F
n
n
(λ) , (56.85)
where λ = na
0
ω
n
n
/V =|∆n|v
B
/(n
2
V),and
F
n
n
(λ) =
2
π
&
tan
−1
2
λ
−
2λ
3λ
2
+20
3
4 +λ
2
2
'
.
(56.86)
Limiting cases:
σ
n
n
∼
2πa
2
s
V/v
2
B
n
3
,λ 1 ,
256σ
elastic
e
−
−B
(
V/v
B
)
3
n
7
15π|∆n|5
,λ 1 ,
(56.87)
where σ
−
e
−B
elastic
is the elastic cross section for e
−
+B
scattering.
(B) Rate Coefficients.
K
n
,n
(T ) =Vσ
n
,n
, (56.88a)
K
n
n
(T ) =
,
(2 +1)
n
2
K
n
,n
, (56.88b)
K
n
n
(T ) =
v
B
σ
elastic
e
−
−B
√
πn
3
(
V
T
/v
B
)
Φ
n
n
(λ
T
), (56.88c)
where
Φ
n
n
(λ
T
) = e
λ
2
T
/8
&
e
λ
2
T
/8
erfc
1
2
λ
T
−
λ
2
T
√
2π
D
−3
λ
T
2
−
5λ
T
√
π
D
−4
λ
T
√
2
(56.89a)
∼
1 −8λ
T
/3
√
π, λ
T
1
2
6
/
√
πλ
5
T
,λ
T
1
,
(56.89b)
where D
−ν
(y) denotes the parabolic cylinder function.
Limiting cases:
K
n
n
(T ) ∼
µR
∞
πm
e
k
B
T
1/2
v
B
σ
elastic
e
−
−B
n
3
,λ
T
→ 0 ,
2
6
v
B
σ
elastic
e−B
n
7
π|∆n|5
$
2k
B
T
µv
2
B
%
2
,λ
T
1 .
(56.90)
Born Results:
σ
n
n
=
8π
k
2
1
n
2
k+k
|k−k
|
F
n
n
(Q)
d(Qa
0
)
(Qa
0
)
3
. (56.91)
(A) Electron–Rydberg Atom Collision.
σ
n
n
=
8πa
2
0
R
∞
Z
2
En
2
1 −
1
4∆n
(εε
)
3/2
(∆ε)
4
ln
(
1 +ε
e
/ε
)
+
1 −
0.6
∆n
ε
e
ε +ε
e
(ε
)
3/2
(∆ε)
2
4
3∆n
+
1
ε
(56.92)
Part D 56.6
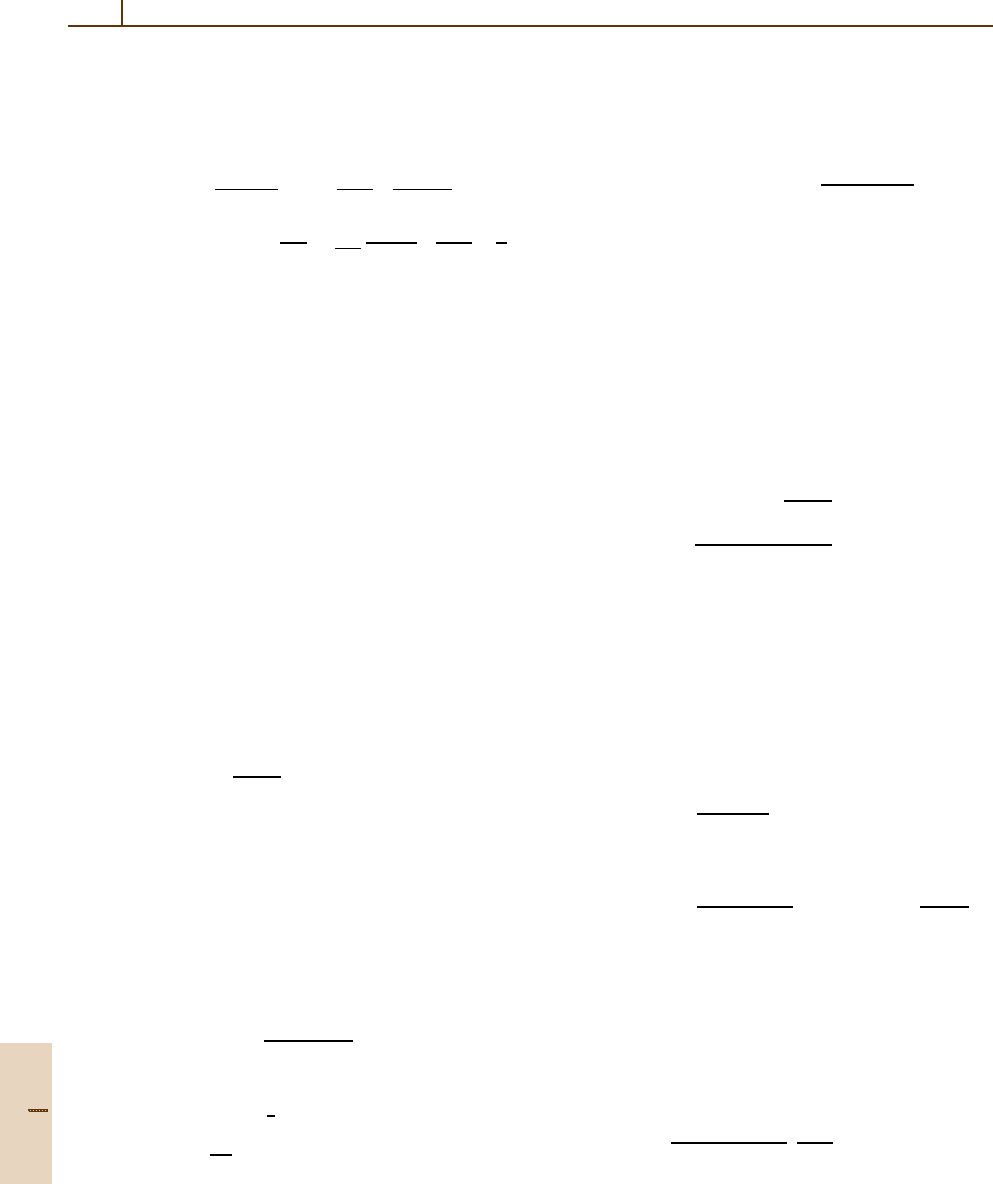
844 Part D Scattering Theory
for n
> n,whereε
e
= E/
Z
2
R
∞
, ε =1/n
2
, ε
= 1/n
2
,
and ∆ε = ε −ε
.
(B) Heavy Particle–Rydberg Atom Collision.
σ
n
n
=
8πa
2
0
Z
2
Z
4
n
2
ε
e
1 −
1
4∆n
(εε
)
3/2
(∆ε)
4
ln(1 +ε
e
/ε)
+
1 −
0.6
∆n
ε
e
ε+ε
e
(ε
)
3/2
(∆ε)
2
4
3∆n
+
1
ε
,
(56.93)
where ε
e
= mε/MZ
2
R
∞
with heavy particle mass and
charge denoted above by M and Z, respectively, and all
other terms retain their meaning as in (56.92).
56.6.3 Quasi-Elastic -Mixing Transitions
σ
(−mixing)
n
≡
=
σ
n
,n
(56.94a)
∼
σ
geo
= 4πa
2
0
n
4
, n n
max
,
2πa
2
s
v
2
B
/V
2
n
3
, n n
max
.
(56.94b)
The two limits correspond to strong (close) coupling for
n n
max
, and weak coupling for n n
max
, and expres-
sions (56.94b) are valid when the quantum defect δ
of
the initial Rydberg orbital n is small. n
max
is the princi-
pal quantum number, where the -mixing cross section
reaches a maximum [56.21],
n
max
∼
v
B
|a
s
|
Va
0
2/7
. (56.95)
For Rydberg atom–noble gas atom scattering, n
max
= 8
to 20, while for Rydberg atom–alkali atom scattering
n
max
= 15 to 30.
56.6.4 Elastic n → n
Transitions
A
∗
(n) + B → A
∗
(n
) +B . (56.96)
(A) Cross Sections.
σ
elastic
ns
(V) =
2πC
ss
a
2
s
(V/v
B
)
2
n
∗4
, (56.97)
valid for n
∗
[
v
B
|a
s
|/(4Va
0
)
]
1/4
with
C
ss
=
8
π
2
1/
√
2
0
[
K(k)
]
2
dk , (56.98)
where K(k) denotes the complete elliptic integral of the
first kind.
(B) Rate Coefficients [56.22] (Three Cases). With the
definitions
ν
B
= v
B
/v
rms
,v
rms
=
(8k
B
T)/µπ , (56.99)
f(y) = y
−1/2
1 −(1 − y)e
−y
+y
3/2
Ei (y),
(56.100)
y = (ν
B
a
s
)
2
(
4πa
2
0
n
∗8
,
(56.101)
n
1
= (|a
s
|ν
B
/4a
0
)
1/4
, (56.102)
n
2
= 0.7
|a
s
|ν
5/6
B
/
α
d
a
3
0
1/6
1/3
, (56.103)
where α
d
is the dipole polarizability of A
∗
,then
)
σ
el
ns
*
∼
8πa
2
0
n
∗4
, n
∗
≤ n
1
,
4π
1/2
a
0
|a
s
|ν
B
f(y), n
1
≤ n
∗
≤ n
2
,
7(α
d
ν
B
)
2/3
+
4a
2
s
ν
2
B
n
∗4
−
2.7a
2
s
ν
2
B
(α
d
ν
B
)
1/3
a
0
n
∗6
, n
∗
≥ n
2
.
(56.104)
56.6.5 Fine Structure
n J → n J
Transitions
A
∗
(nJ) +B → A
∗
(nJ
) +B+∆E
J
J
. (56.105)
(A) Cross Sections (Two Cases).
σ
nJ
nJ
(V) =
2J
+1
2(2 +1)
c
norm
4πa
2
0
n
∗4
, (56.106)
valid for n
∗
≤ n
0
(V),and
σ
nJ
nJ
(V) =
2πC
()
J
J
a
2
s
v
2
B
V
2
n
∗4
ϕ
()
J
J
(ν
J
J
)
$
1 −
n
8
0
(V)
2n
∗8
%
,
(56.107)
valid for n
∗
≥ n
0
(V), where the quantity n
0
(V) is the
effective principal quantum number such that the impact
parameter ρ
0
of B (moving with relative velocity V)
equals the radius 2n
∗2
a
0
of the Rydberg atom A
∗
. n
0
(V)
is given by the solution to the following transcendental
equation
n
8
0
(V)=
(2+1)C
()
J
J
2(2J
+1)c
norm
v
B
a
s
Va
0
2
ϕ
()
J
J
ν
J
J
[
n
0
(V)
]
.
(56.108)
Part D 56.6
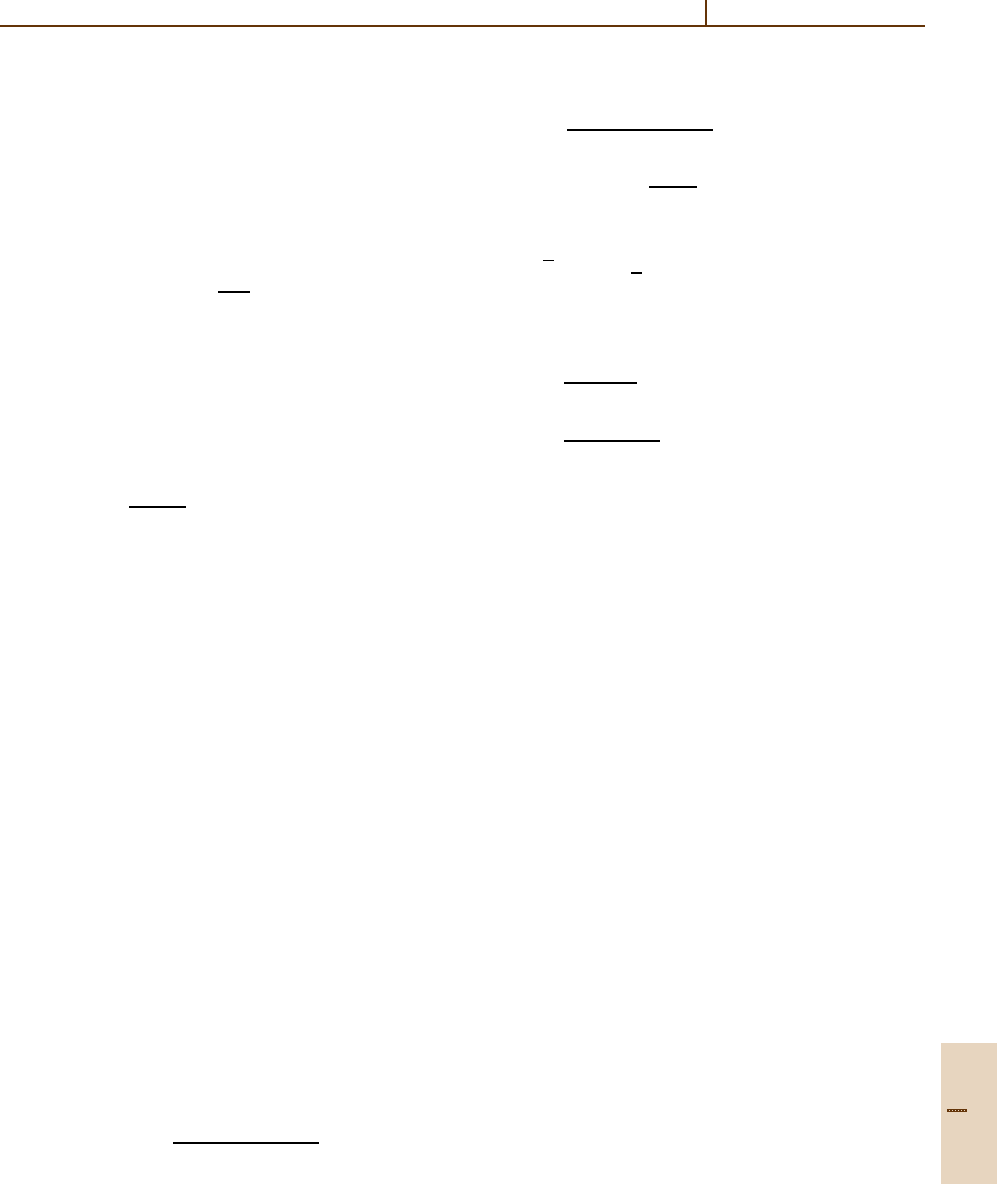
Rydberg Collisions: Binary Encounter, Born and Impulse Approximations 56.7 Impulse Approximation 845
The constant c
norm
in (56.106) is equal to 5/8ifσ
geo
=
πr
2
n
,or1ifσ
geo
= 4πa
2
0
n
∗4
. The function ϕ
()
J
J
(ν
J
J
)
in (56.107) is given in general by [56.23, 24]
ϕ
()
J
J
(ν
J
J
) = ξ
()
J
J
(ν
J
J
)/ξ
()
J
J
(0), (56.109a)
ξ
()
J
J
(ν
J
J
) =
s=0
A
(2s)
J
,J
∞
ν
J
J
j
2
s
(z)J
2
s
(z)zdz ,
(56.109b)
ν
J
J
=|δ
J
−δ
J
|
v
B
Vn
∗
, (56.109c)
where j
s
(z) is the spherical Bessel function and
the coefficients C
()
J
J
and A
(2s)
J
,J
in (56.107)and
(56.109b), respectively, are given in table 5.1 of Beigman
and Lebedev [56.6]. The quantum defect of Rydberg
state nJ is δ
J
. For elastic scattering, ν
JJ
= 0, and
ϕ
()
JJ
(0) = 1.
Symmetry relation:
ξ
()
JJ
(ν
J
J
) =
2J +1
2J
+1
ξ
()
J
J
(ν
J
J
). (56.110)
(B) Rate Coefficients.
σ
nJ
nJ
=
$
c
norm
(2J
+1)C
()
J
J
2(2 +1)
%
1/2
× πa
2
0
F(ζ)
v
B
|a
s
|
V
T
a
0
,
(56.111)
where ζ = n
8
0
(V
T
)/n
∗8
,and
F(ζ) ≡
ζ
E
2
(ζ) +
1
ζ
(1 − e
−ζ
)
, (56.112)
where E
2
(x) is an exponential integral.
Limiting cases:
)
σ
nJ
nJ
*
=
2J
+1
2(2 +1)
c
norm
4πa
2
0
n
∗4
, n
∗
n
∗
max
,
2πC
()
J
J
a
2
s
v
2
B
V
2
T
n
∗4
, n
∗
n
∗
max
,
(56.113)
where n
∗
max
= (3/2)
1/8
n
0
(V) if ν
J
J
1.
56.7 Impulse Approximation
56.7.1 Quantal Impulse Approximation
Basic Formulation [56.25]
Consider a Rydberg collision between a projectile (1)
of charge Z
1
and a target with a valence electron (3) in
orbital ψ
i
bound to a core (2). The full three-body wave
function for the system of projectile + target is denoted
by Ψ
i
. The relative distance between 1 and the center-
of-mass of 2 −3 is denoted by σ , while the separation
of 2 from the center-of-mass of 1 −3isρ.
Formal Scattering Theory.
Ψ
(+)
i
= Ω
(+)
ψ
i
, (56.114)
where the Möller scattering operator Ω
(+)
= 1 +G
+
V
i
,
and V
i
= V
12
+V
13
.
Let χ
m
be a complete set of free-particle wave
functions satisfying
(H
0
−E
m
)χ
m
= 0 , (56.115)
and define operators ω
+
ij
(m) by
ω
+
ij
(m)χ
m
=
1 +
1
E
m
− H
0
−V
ij
+i
V
ij
χ
m
,
(56.116)
where V
ij
denotes the pairwise interaction potential be-
tween particles i and j (i, j = 1, 2, 3). Then the action of
the full Green’s function G
+
on the two-body potential
V
ij
is
G
+
V
ij
=
ω
+
ij
(m) −1
+G
+
(E
m
−E)+V
12
+V
13
+V
23
−V
ij
×
ω
+
ij
(m) −1
. (56.117)
Projection Operators.
b
+
ij
(m) =ω
+
ij
(m) −1 , (56.118a)
b
+
ij
=
m
b
+
ij
(m)|χ
m
χ
m
| ,ω
+
ij
= b
+
ij
+1 .
(56.118b)
G
+
V
ij
|ψ
i
=
m
G
+
V
ij
|χ
m
χ
m
|ψ
i
(56.119a)
=
b
+
ij
+G
+
V
23
, b
+
ij
+G
+
V
12
+V
13
−V
ij
b
+
ij
(m)
|ψ
i
.
(56.119b)
Part D 56.7
