Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics
Подождите немного. Документ загружается.

Electron–Ion and Ion–Ion Recombination 54.7 Microscopic Methods for Termolecular Ion–Ion Recombination 815
Bottleneck Method
The one-way equilibrium rate
cm
−3
s
−1
across −E,
i. e., (54.141c) with ρ
i
=1andρ
f
=0, is
ˆ
α(−E)
˜
N
A
˜
N
B
=
∞
−E
dE
i
−E
−D
C
if
dE
f
. (54.150)
This is an upper limit to (54.141c) and exhibits a min-
imum at −E
∗
, the bottleneck location. The least upper
limit to
ˆ
α is then
ˆ
α(−E
∗
).
Trapping Radius Method
Assume that pairs with internal separation R ≤ R
T
re-
combine with unit probability so that the one-way
equilibrium rate across the dissociation limit at E = 0
for these pairs is
ˆ
α(R
T
)
˜
N
A
˜
N
B
=
R
T
0
dR
0
V(R)
C
if
(R) dE
f
, (54.151)
where V(R) =−e
2
/R ,andC
if
(R) =
˜
n
i
(R)ν
if
(R) is the
rate per unit interval (dRdE
i
)dE
f
for the E
i
→ E
f
collisional transitions at fixed R in
A
+
−B
−
E
i
,R
+M →
A
+
−B
−
E
f
,R
+M .
(54.152)
The concentration
cm
−3
of pairs with internal
separation R and orbital energy E
i
in the interval
dRdE
i
about (R, E
i
) is
˜
n
i
(R) dRdE
i
. Agreement with
the exact treatment [54.13] is found by assigning
R
T
=(0.48 - 0.55)
e
2
/k
B
T
for the recombination of
equal mass ions in an equal mass gas for various ion–
neutral interactions. For further details on the above
methods, see the appropriate references on termolecular
recombination in the general references on page 825.
54.7.3 Recombination
at Higher Gas Densities
As the density N of the gas M is raised, the recombin-
ation rate
ˆ
α increases initially as N to such an extent that
there are increasingly more pairs n
−
i
(R, E) in a state of
contraction in R than there are those n
+
i
(R, E) in a state
of expansion; i. e., the ion-pair distribution densities
n
±
i
(R, E) per unit interval dE dR are not in equilib-
rium with respect to R in blocks C and E . Those in the
highly excited block E in addition are not in equilib-
rium with respect to energy E. Basic sets of coupled
master equations have been developed [54.13]forthe
microscopic nonequilibrium distributions n
±
R, E, L
2
and n
±
(R, E) of expanding (+) and contracting (−)
pairs with respect to A–B separation R, orbital en-
ergy E and orbital angular momentum L
2
. With
n
R, E
i
, L
2
i
≡ n
i
(R), and using the notation defined
at the beginning of Sect. 54.6, the distinct regimes
for the master equations discussed in Sect. 54.7.4 are:
Low N Equilibrium in R, but not in E, L
2
→ master equation for n
E, L
2
.
Pure Coulomb Equilibrium in L
2
attraction → master equation for n(E).
High N Nonequilibrium in R, E, L
2
→ master equation for n
±
i
(R).
Highest N Equilibrium in
E, L
2
but not in R
→ macroscopic transport equation
(54.56a)inn(R).
Normalized Distributions
For a state
|
i
≡
E, L
2
,
ρ
i
(R) =
n
i
(R)
˜
n
i
(R)
,ρ
±
i
(R) =
n
±
i
(R)
˜
n
±
i
(R)
,
ρ
i
(R) =
1
2
ρ
+
i
+ρ
−
i
.
(54.153)
Orbital Energy and Angular Momentum
E
i
=
1
2
M
AB
v
2
+V(R), (54.154a)
E
i
=
1
2
M
AB
v
2
R
+V
i
(R), (54.154b)
V
i
(R) = V(R) +
L
2
i
2M
AB
R
2
, (54.154c)
L
i
=
|
R× M
AB
v
|
,
L
2
i
=(2M
AB
E
i
)b
2
, E
i
> 0 . (54.154d)
Maximum Orbital Angular Momenta
(1) A specified separation R can be accessed by all orbits
of energy E
i
with L
2
i
between 0 and
L
2
im
(E
i
, R) = 2M
AB
R
2
[
E
i
−V(R)
]
. (54.155a)
(2) Bounded orbits of energy E
i
< 0 can have L
2
i
be-
tween 0 and
L
2
ic
(E
i
) =2M
AB
R
2
c
[
E
i
−V(R
c
)
]
, (54.155b)
where R
c
is the radius of the circular orbit determined
by ∂V
i
/∂R =0, i. e., by E
i
= V(R
c
) +
1
2
R
c
(∂V/∂R)
R
c
.
Part D 54.7
816 Part D Scattering Theory
54.7.4 Master Equations
Master Equation for n
±
i
(R)
±
R, E
i
, L
2
i
[54.13]
±
1
R
2
∂
∂R
R
2
n
±
i
(R)
|
v
R
|
E
i
,L
2
i
=−
∞
V(R)
dE
f
L
2
f m
0
dL
2
f
n
±
i
(R)ν
if
(R)
−n
±
f
(R)ν
fi
(R)
. (54.156)
The set of master equations [54.13]forn
+
i
is coupled
to the n
−
i
set by the boundary conditions n
−
i
R
∓
i
=
n
+
i
R
∓
i
at the pericenter R
−
i
for all E
i
and apocenter
R
+
i
for E
i
< 0oftheE
i
, L
2
i
-orbit.
Master Equations
for Normalized Distributions [54.13]
±
|
v
R
|
∂ρ
±
i
∂R
=−
∞
V(R)
dE
f
L
2
f m
0
dL
2
f
(54.157)
×
ρ
±
i
(R) −ρ
±
f
(R)
ν
if
(R).
Corresponding Master equations for the L
2
integrated
distributions n
±
(R, E) and ρ
±
(R, E) have been de-
rived [54.13].
Continuity Equations
J
i
=
n
+
i
(R) −n
−
i
(R)
|
v
R
|
=
ρ
+
i
−ρ
−
i
˜
j
±
i
(54.158)
1
R
2
∂
∂R
(R
2
J
i
) =−
∞
V(R)
dE
f
L
2
f m
0
dL
2
f
×
n
i
(R)ν
if
(R) −n
f
(R)ν
fi
(R)
,
(54.159)
1
2
|
v
R
|
∂
ρ
+
i
(R) −ρ
−
i
(R)
∂R
=−
∞
V(R)
dE
f
L
2
f m
0
dL
2
f
ρ
i
(R) −ρ
f
(R)
ν
if
(R).
(54.160)
54.7.5 Recombination Rate
Flux Representation
The R
0
→∞limit of
ˆ
α
˜
N
A
˜
N
B
=−4πR
2
0
J(R
0
) (54.161)
has the microscopic generalization
ˆ
α
˜
N
A
˜
N
B
=
∞
V(R
0
)
dE
i
L
2
ic
0
dL
2
i
4πR
2
0
˜
j
±
i
(R
0
)
×
ρ
−
i
(R
0
) −ρ
+
i
(R
0
)
, (54.162)
where L
2
ic
is given by (54.155b) with R
c
= R
0
for bound
states and is infinite for dissociated states, and where
ρ
−
i
(R
0
) −ρ
+
i
(R
0
) =
R
0
R
i
ρ
i
(R)
ν
b
i
(R) +ν
c
i
(R)
dt ,
(54.163)
with
ρ
i
(R)ν
b
i
(R) =
V(R
0
)
V(R)
dE
f
L
2
f m
0
dL
2
f
ρ
i
(R) −ρ
f
(R)
× ν
if
(R), (54.164a)
ρ
i
(R)ν
c
i
(R) =
∞
V(R
0
)
dE
f
L
2
f m
0
dL
2
f
ρ
i
(R) −ρ
f
(R)
× ν
if
(R). (54.164b)
Collisional Representation
ˆ
α
˜
N
A
˜
N
B
=
∞
V(R
0
)
dE
i
L
2
ic
0
dL
2
i
R
0
R
i
˜
n
i
(R) dR
×
ρ
i
(R)ν
b
i
(R)
, (54.165)
which is the microscopic generalization of the macro-
scopic result
ˆ
α = Kρ
∗
ν
s
=α
RN
(R
0
)ρ(R
0
).
The flux for dissociated pairs E
i
> 0is
4πR
2
|
v
R
|
˜
n
±
i
(R) dE dL
2
=
vεe
−ε
dε
[
2πb db
]
˜
N
A
˜
N
B
, (54.166)
so the rate (54.165)asR
0
→∞is
ˆ
α =
v
∞
0
εe
−ε
dε
b
0
0
2πb db
R
0
R
i
ρ
i
(R)ν
b
i
(R) dt ,
(54.167)
Part D 54.7
Electron–Ion and Ion–Ion Recombination 54.8 Radiative Recombination 817
which is the microscopic generalization (54.45)ofthe
macroscopic result
ˆ
α = k
c
P
S
of (54.44).
Reaction Rate α
RN
(R
0
)
On solving (54.157) subject to ρ(R
0
) =1, then
according to (54.56b),
ˆ
α determined by (54.162)
is the rate
ˆ
α
RN
of recombination within the
(A − B) sphere of radius R
0
. The overall rate
of recombination
ˆ
α is then given by the full
diffusional-drift reaction rate (54.59b)wherethe
rate of transport to R
0
is determined uniquely by
(54.60).
For development of theory [54.13] and computer
simulations, see the reference list on Termolecu-
lar Ion–Ion Recombination: Theory, and Simulations,
respectively.
54.8 Radiative Recombination
In the radiative recombination (RR) process
e
−
(E,
) + A
Z+
(c) → A
(Z−1)+
(c, n) +hν,
(54.168)
the accelerating electron e
−
with energy and angular
momentum (E,
) is captured, via coupling with the
weak quantum electrodynamical interaction (e/m
e
c)A·
p associated with the electromagnetic field of the mov-
ing ion, into an excited state n with binding energy I
n
about the parent ion A
Z+
(initially in an electronic
state c). The simultaneously emitted photon carries away
the excess energy hν = E +I
n
and angular momentum
difference between the initial and final electronic states.
The cross section σ
n
R
(E) for RR is calculated (a) from
the Einstein A coefficient for free–bound transitions
or (b) from the cross section σ
n
I
(hν) for photoion-
ization (PI) via the detailed balance (DB) relationship
appropriate to (54.168).
The rates
v
e
σ
R
and averaged cross sections
σ
R
for a Maxwellian distribution of electron speeds v
e
are
then determined from either
ˆ
α
n
R
(T
e
) =v
e
∞
0
εσ
n
R
(ε) exp(−ε)dε
=
v
e
-
σ
n
R
(T
e
)
.
, (54.169)
where ε = E/k
B
T
e
, or from the Milne DB relation
(54.243) between the forward and reverse macroscopic
rates of (54.168). Using the hydrogenic semiclassical σ
n
I
of Kramers [54.5], together with an asymptotic ex-
pansion [54.14]fortheg-factor of Gaunt [54.15], the
quantal/semiclassical cross section ratio in (54.249),
Seaton [54.16] calculated
ˆ
α
n
R
.
The rate of electron energy loss in RR is
/
dE
dt
0
n
=n
e
v
e
(k
B
T
e
)
∞
0
ε
2
σ
n
R
(ε) e
−ε
dε,
(54.170)
and the radiated power produced in RR is
/
d(hν)
dt
0
n
= n
e
v
e
∞
0
εhνσ
n
R
(ε) e
−ε
dε. (54.171)
Standard Conversions
E = p
2
e
/2m
e
=
2
k
2
e
/2m
e
=k
2
e
a
2
0
e
2
/2a
0
(54.172a)
=κ
2
Z
2
e
2
/2a
0
= ε
Z
2
e
2
/2a
0
,
(54.172b)
E
ν
= hν = ω = k
ν
c = (I
n
+E) (54.172c)
≡
1+n
2
ε
Z
2
e
2
/2n
2
a
0
,
(54.172d)
hν/I
n
=1+n
2
ε, k
2
e
a
2
0
=2E/
e
2
/a
0
,
(54.172e)
k
ν
a
0
=(hν)α/
e
2
/a
0
,
(54.172f)
k
2
ν
/k
2
e
=(hν)
2
/
2Em
e
c
2
(54.172g)
=α
2
(hν)
2
/
2E
e
2
/a
0
,
(54.172h)
I
H
=e
2
/2a
0
,α=e
2
/ c = 1/137.035 9895 ,
α
−2
=m
e
c
2
/
e
2
/a
0
, I
n
=
Z
2
/n
2
I
H
.
(54.172i)
The electron and photon wavenumbers are k
e
and k
ν
,
respectively.
54.8.1 Detailed Balance
and Recombination-Ionization
Cross Sections
Cross sections σ
n
R
(E) and σ
n
I
(hν) for radiative re-
combination (RR) into and photoionization (PI) out
of level n of atom A are interrelated by the detailed
balance relation
g
e
g
+
A
k
2
e
σ
n
R
(E) = g
ν
g
A
k
2
ν
σ
n
I
(hν) , (54.173)
where g
e
= g
ν
= 2. Electronic statistical weights of
A and A
+
are g
A
and g
+
A
, respectively. Thus, using
Part D 54.8
818 Part D Scattering Theory
(54.172g)fork
2
ν
/k
2
e
,
σ
n
R
(E) =
g
A
2g
+
A
(hν)
2
Em
e
c
2
σ
n
I
(hν) . (54.174)
The statistical factors are:
(a) For
A
+
+ e
−
state c
S
c
, L
c
;ε,
, m
:
g
+
A
=(2S
c
+1)(2L
c
+1).
(b) For A(n) state b[S
c
, L
c
;n,]SL :
g
A
= (2S +1)(2L +1).
(c) For n electron outside a closed shell:
g
+
A
=1, g
A
= 2(2 +1).
Cross sections are averaged over initial and summed
over final degenerate states. For case (c),
σ
n
I
=
1
n
2
n−1
=0
(2 +1)σ
n
I
; (54.175a)
σ
n
R
=
n−1
=0
2(2 +1)σ
n
R
. (54.175b)
54.8.2 Kramers Cross Sections, Rates,
Electron Energy-Loss Rates
and Radiated Power
for Hydrogenic Systems
These are all calculated from application of detailed bal-
ance (54.173) to the original σ
n
I
(hν) of Kramers [54.5].
Semiclassical (Kramers) Cross Sections
For hydrogenic systems,
I
n
=
Z
2
e
2
2n
2
a
0
, hν = I
n
+E . (54.176)
The results below are expressed in terms of the quantities
b
n
=
I
n
k
B
T
e
, (54.177)
σ
n
I0
=
64πa
2
0
α
3
√
3
n
Z
2
=7.907 071 × 10
−18
n/Z
2
cm
2
,
(54.178)
σ
R0
(E) =
8πa
2
0
α
3
3
√
3
Z
2
e
2
/a
0
E
,
(54.179)
ˆ
α
0
(T
e
) =v
e
8πa
2
0
α
3
3
√
3
Z
2
e
2
/a
0
k
B
T
e
(54.180)
PI and RR Cross Sections for Level n. In the Kramer (K)
semiclassical approximation,
K
σ
n
I
(hν) =
I
n
hν
3
σ
n
I0
=
K
σ
n
I
(hν) , (54.181)
K
σ
n
R
(E) = σ
R0
(E)
2
n
I
n
I
n
+E
(54.182)
=3.897×10
−20
×
nε
13.606+n
2
ε
2
−1
cm
2
,
where ε is in units of eV and is given by
ε = E/Z
2
≡
2.585×10
−2
/Z
2
T
e
/300
.
(54.183)
Equation (54.182) illustrates that RR into low n at low E
is favored.
Cross Section for RR into Level n.
K
σ
n
R
=
(2 +1)/n
2
K
σ
n
R
. (54.184)
Rate for RR into Level n.
ˆ
α
n
R
(T
e
) =
ˆ
α
0
(T
e
)
(
2/n
)
b
n
e
b
n
E
1
(b
n
), (54.185a)
which tends for large b
n
(i. e., k
B
T
e
I
n
)to
ˆ
α
n
R
(T
e
→0) =
ˆ
α
0
(T
e
)
(
2/n
)
×
1−b
−1
n
+2b
−2
n
−6b
−3
n
+···
.
(54.185b)
The Kramers cross section for photoionization at
threshold is σ
n
I0
and
σ
n
R0
=2σ
R0
/n;
ˆ
α
n
0
=2
ˆ
α
0
/n (54.186)
provide the corresponding Kramers cross section
and rate for recombination as E → 0andT
e
→ 0,
respectively.
RR Cross Sections and Rates into All Levels n ≥n
f
.
σ
T
R
(E) =
∞
n
f
σ
n
R
(E) dn
=σ
R0
(E) ln(1+I
f
/E), (54.187a)
ˆ
α
T
R
(T
e
) =
ˆ
α
0
(T
e
)
γ +ln b
f
+ e
b
f
E
1
(b
f
)
(54.187b)
Part D 54.8
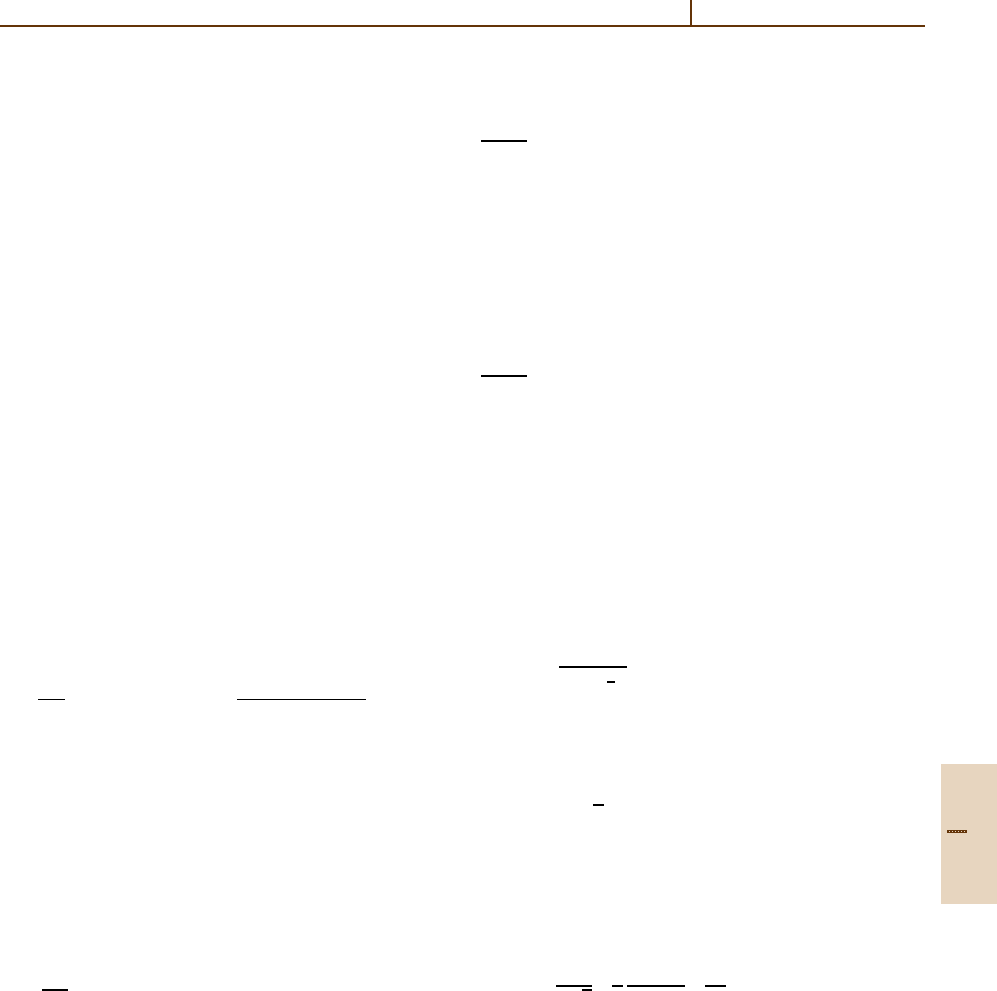
Electron–Ion and Ion–Ion Recombination 54.8 Radiative Recombination 819
Useful Integrals.
∞
0
e
−x
ln x dx = γ, (54.188a)
∞
b
x
−1
e
−x
dx = E
1
(b), (54.188b)
b
0
e
x
E
1
(x) dx = γ +ln b + e
b
E
1
(b), (54.188c)
b
0
1−x e
x
E
1
(x)
dx
=γ +ln b + e
b
(1−b)E
1
(b), (54.188d)
where γ =0.577 2157 is Euler’s constant, and E
1
(b) is
the first exponential integral such that
be
b
E
1
(b)
b1
−→ 1 −b
−1
+2b
−2
−6b
−3
+24b
−4
+···.
Electron Energy Loss Rate
Energy Loss Rate for RR into Level n.
/
dE
dt
0
n
=n
e
ˆ
α
n
R
(T
e
)k
B
T
e
1−b
n
e
b
n
E
1
(b
n
)
e
b
n
E
1
(b
n
)
,
(54.189a)
which for large b
n
(i. e. (k
B
T
e
) I
n
) tends to
n
e
ˆ
α
n
R
(T
e
)k
B
T
e
1−b
−1
n
+3b
−2
n
−13b
−3
n
+···
(54.189b)
with (54.185a)for
ˆ
α
n
R
.
Energy Loss Rate for RR into All Levels n ≥n
f
.
/
dE
dt
0
=n
e
k
B
T
e
ˆ
α
0
(T
e
)
γ +ln b
f
+ e
b
f
E
1
(b
f
)(1−b
f
)
(54.190a)
=n
e
(k
B
T
e
)
ˆ
α
T
R
(T
e
) −
ˆ
α
0
(T
e
)b
f
e
b
f
E
1
(b
f
)
(54.190b)
with (54.187b)and(54.180)for
ˆ
α
T
R
and
ˆ
α
0
.
Radiated Power
Radiated Power for RR into Level n.
/
d(hν)
dt
0
n
=n
e
ˆ
α
n
R
(T
e
)I
n
b
n
e
b
n
E
1
(b
n
)
−1
,
(54.191a)
which for large b
n
(i. e. (k
B
T
e
) I
n
) tends to
n
e
ˆ
α
n
R
(T
e
)I
n
1+b
−1
n
−b
−2
n
+3b
−3
n
+···
.
(54.191b)
Radiated Power for RR into All Levels n ≥n
f
.
/
d(hν)
dt
0
=n
e
ˆ
α
0
(T
e
)I
f
. (54.192)
To allow n-summation, rather than integration as in
(54.187a), to each of the above expressions is added
1/2σ
n
f
R
,1/2
ˆ
α
n
f
R
,1/2dE/dt
n
f
and 1/2d(hν)/dt
n
f
,
respectively. The expressions valid for bare nuclei of
charge Z are also fairly accurate for recombination to
a core of charge Z
c
and atomic number Z
A
, provided
that Z is identified as 1/2(Z
A
+Z
c
).
Differential Cross Sections for Coulomb Elastic Scat-
tering.
σ
c
(E,θ)=
b
2
0
4sin
4
1
2
θ
, b
2
0
=(Ze
2
/2E)
2
.
(54.193)
The integral cross section for Coulomb scattering by
θ ≥ π/2atenergyE = (3/2)k
B
T is
σ
c
(E) = πb
2
0
=
1
9
πR
2
e
, R
e
=e
2
/k
B
T . (54.194)
Photon Emission Probability.
P
ν
=σ
n
R
(E)/σ
c
(E). (54.195a)
This is small and increases with decreasing n as
P
ν
(E) =
8α
3
3
√
3
8
n
E
(e
2
/a
0
)
I
n
hν
.
(54.195b)
54.8.3 Basic Formulae for Quantal Cross
Sections
Radiative Recombination
and Photoionization Cross Sections
The cross section σ
n
R
for recombination follows from
the continuum-bound transition probability P
if
per unit
Part D 54.8
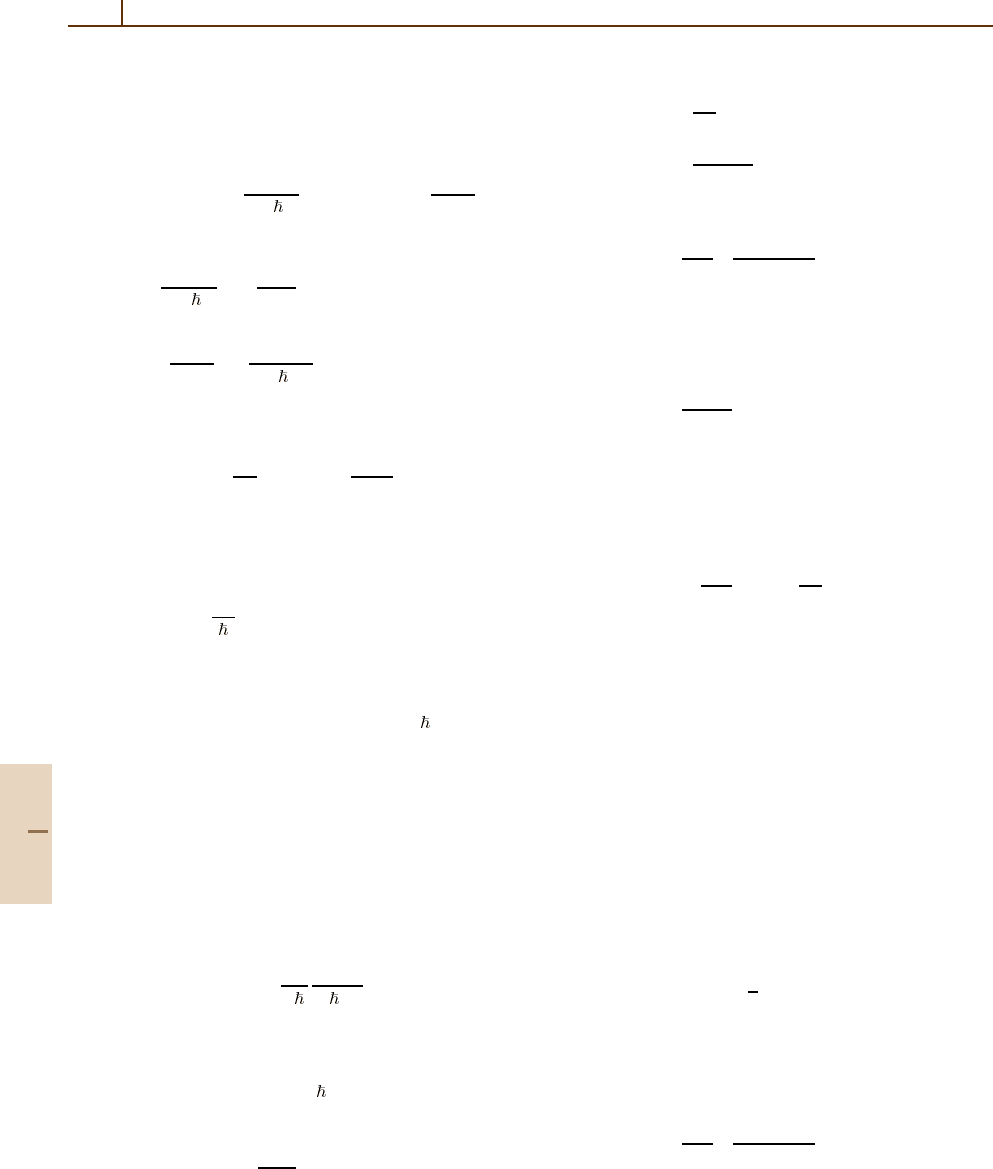
820 Part D Scattering Theory
time. It is also provided by the detailed balance relation
(54.173)intermsofσ
n
I
which follows from P
fi
.The
number of radiative transitions per second is
g
e
g
+
A
ρ(E) dE d
ˆ
k
e
P
if
ρ(E
ν
) dE
ν
d
ˆ
k
ν
= g
e
g
+
A
v
e
dp
e
(2π )
3
σ
R
(k
e
) = g
ν
g
A
c
dk
ν
(2π)
3
σ
I
(k
ν
),
(54.196)
where the electron current
cm
−2
s
−1
is
v
e
dp
e
(2π )
3
=
2mE
h
3
dE d
ˆ
k
e
, (54.197)
and the photon current
cm
−2
s
−1
is
c
dk
ν
(2π)
3
=c
(hν)
2
(2π c)
3
dE
ν
d
ˆ
k
ν
. (54.198)
Time Dependent Quantum Electrodynamical Inter-
action.
V(r, t) =
e
mc
A· p = ie
2πhν
V
1/2
(
ˆ
· r)e
−i(k
ν
·r−ωt)
≡ V(r) e
iωt
. (54.199)
In the dipole approximation, e
−ik
ν
·r
≈1.
Continuum-Bound State-to-State Probability.
P
if
=
2π
V
fi
2
δ
[
E
ν
−(E +I
n
)
]
V
fi
=
Ψ
nm
(r)
|
V(r)
|
Ψ
i
(r, k
e
)
. (54.200)
Number of Photon States in Volume V.
ρ
E
ν
,
ˆ
k
ν
dE
ν
d
ˆ
k
ν
=V(hν)
2
/(2π c)
3
dE
ν
d
ˆ
k
ν
(54.201a)
=V
ω
2
/(2πc)
3
dω d
ˆ
k
ν
.
(54.201b)
Continuum-Bound Transition Rate. On summing over
the two directions (g
ν
= 2) of polarization, the rate for
transitions into all final photon states is
A
nm
E,
ˆ
k
e
=
P
if
ρ(E
ν
) dE
ν
d
ˆ
k
ν
=
4e
2
3
(hν)
3
(3 c)
3
|
Ψ
nm
|r|Ψ
i
(k
e
)
|
2
.
(54.202)
Transition Frequency: Alternative Formula.
A
nm
E,
ˆ
k
e
=(2π/
)
D
fi
2
, (54.203)
where the dipole atom-radiation interaction coupling is
D
fi
(k
e
) =
2ω
3
3πc
3
1/2
Ψ
nm
|e r|Ψ
i
(k
e
)
. (54.204)
RR Cross Section into Level (nm).
σ
nm
R
(E) =
1
4π
σ
nm
R
(k
e
)d
ˆ
k
e
=
h
3
ρ(E)
8πm
e
E
A
nm
E,
ˆ
k
e
d
ˆ
k
e
. (54.205)
RR Cross Section into Level (n).
σ
n
R
(E) =
8π
2
3
(αhν)
3
2(e
2
/a
0
)E
ρ(E)R
n
I
(E)
R
n
I
(E) =
d
ˆ
k
e
m
|
Ψ
nm
|r|Ψ
i
(k
e
)
|
2
. (54.206)
Transition T-Matrix for RR.
σ
n
R
(E) =
πa
2
0
(ka
0
)
2
|
T
R
|
2
ρ(E), (54.207)
|
T
R
|
2
=4π
2
m
D
fi
2
d
ˆ
k
e
. (54.208)
Photoionization Cross Section. From detailed balance
in (54.196), σ
n
I
is
σ
n
I
(hν) =
8π
2
3
αhν
g
+
A
g
A
ρ(E)R
n
I
(E).
(54.209)
Continuum Wave Function Expansion.
Ψ
i
(k
e
, r) =
m
i
e
iη
R
E
(r)Y
m
ˆ
k
e
Y
m
(
ˆ
r).
(54.210)
Energy Normalization. With ρ(E) =1,
Ψ
i
(k
e
;r)Ψ
∗
i
k
e
;r
dr =δ
E − E
δ
ˆ
k
e
−
ˆ
k
e
.
(54.211)
Plane Wave Expansion.
e
ik·r
=4π
∞
=0
i
j
(kr)Y
∗
m
ˆ
k
Y
m
(
ˆ
r) (54.212)
j
(kr) ∼sin
kr −
1
2
π
/(kr).
(54.213)
For bound states,
Ψ
nm
(r) = R
n
(r)Y
m
(
ˆ
r). (54.214)
RR and PI Cross Sections and Radial Integrals.
σ
n
R
(E) =
8π
2
3
(αhν)
3
2(e
2
/a
0
)E
ρ(E)R
I
(E;n) .
(54.215)
Part D 54.8
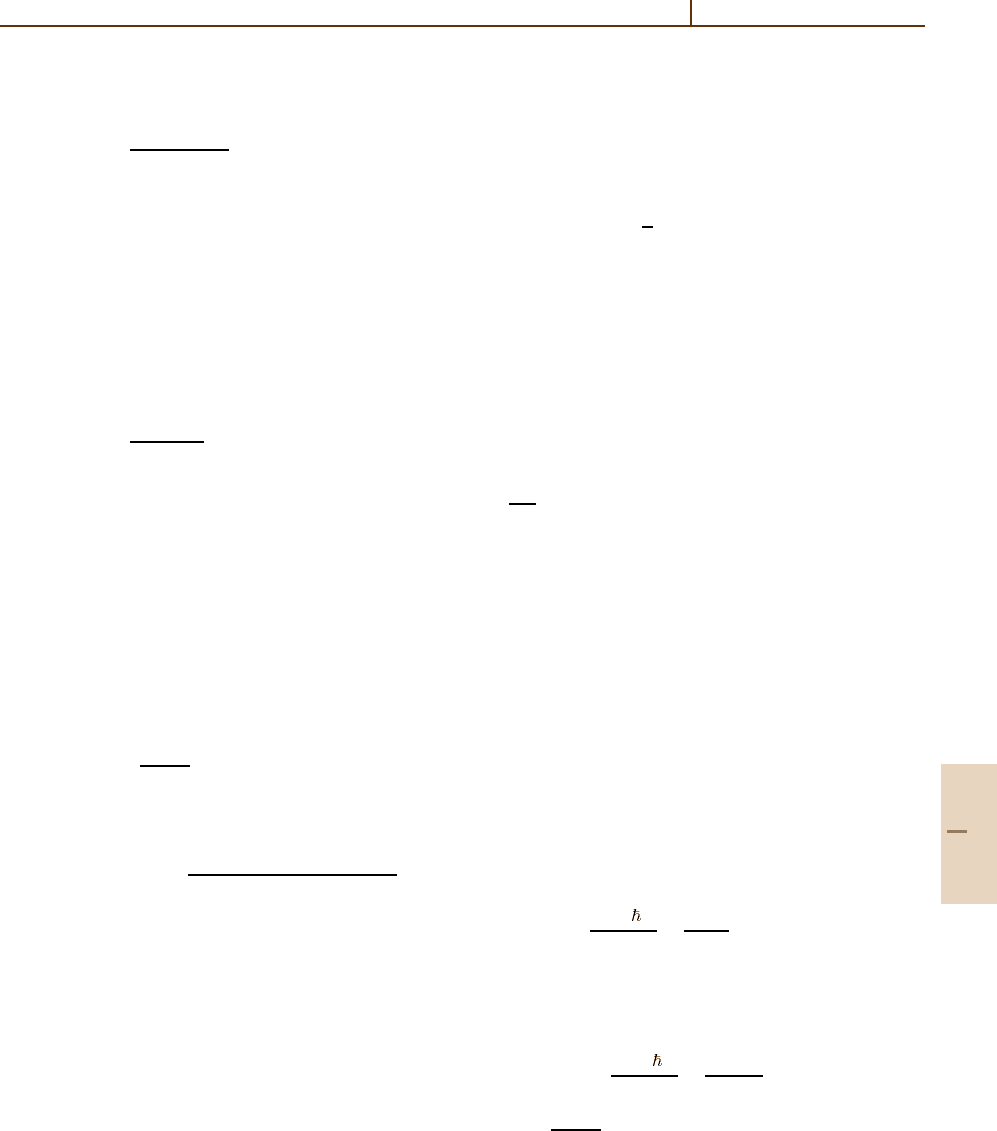
Electron–Ion and Ion–Ion Recombination 54.8 Radiative Recombination 821
For an electron outside a closed core,
g
+
A
=1, g
A
=2(2 +1)
σ
n
I
(hν) =
4π
2
αhνρ(E )
3(2 +1)
R
I
(E;n) , (54.216a)
R
ε,
n
=
∞
0
(
R
ε
rR
n
)
r
2
dr , (54.216b)
R
I
(E;n) =
R
ε,−1
n
2
+( +1)
R
ε,+1
n
2
.
(54.216c)
For an electron outside an unfilled core (c) in the
process
A
+
+ e
−
→ A(n), the weights are
State i:
[
S
c
, L
c
;ε
]
, g
+
A
=(2S
c
+1)(2L
c
+1)
State f :
[
(S
c
, L
c
;n)S, L
]
, g
A
= (2S +1)(2L +1).
R
I
(E;n) =
(2L +1)
(2L
c
+1)
×
=±1
L
2L
+1
LL
c
L
1
!
2
×
max
∞
0
(
R
ε
rR
n
)
r
2
dr
2
.
(54.217)
This reduces to (54.216c) when the radial functions R
i, f
do not depend on (S
c
, L
c
, S, L).
Cross Section for Dielectronic Recombination
σ
n
DLR
(E) =
πa
2
0
(ka
0
)
2
|
T
DLR
(E)
|
2
ρ(E), (54.218)
|
T
DLR
(E)
|
2
=4π
2
d
ˆ
k
e
×
j
Ψ
f
D
Ψ
j
Ψ
j
V
|
Ψ
i
(k
e
)
E −ε
j
+iΓ
j
/2
2
,
(54.219)
which is the generalization of the T -matrix (54.208)
to include the effect of intermediate doubly-excited
autoionizing states
Ψ
j
in energy resonance to within
width Γ
j
of the initial continuum state Ψ
i
.The
electrostatic interaction V = e
2
1
N
i=1
(r
i
−r
N+1
)
−1
ini-
tially produces dielectronic capture by coupling the
initial state i with the resonant states j which be-
come stabilized by coupling via the dipole radiation
field interaction D =
2ω
3
/3πc
3
1/2
1
N+1
i=1
(er
i
) to
the final stabilized state f . The above cross section for
(54.3) is valid for isolated, nonoverlapping resonances.
Continuum Wave Normalization
and Density of States
The basic formulae (54.206)forσ
n
R
depends on the
density of states ρ(E) which in turn varies according to
the particular normalization constant N adopted for the
continuum radial wave,
R
E
(r) ∼ N sin
kr −
1
2
π +η
2
r ,
(54.220)
in (54.210) where the phase is
η
=arg Γ( +1+iβ) −β ln 2kr +δ
. (54.221)
The phase corresponding to the Hartree–Fock short-
range interaction is δ
. The Coulomb phase shift for
electron motion under
−Ze
2
/r
is (η
−δ
) with
β = Z/(ka
0
).
For a plane wave φ
k
(r) = N
exp(ik· r),
φ
k
(r)|φ
k
(r)
dk = (2π)
3
N
2
ρ(k) dkδ
k−k
≡
h
3
mp
N
2
ρ(E,
ˆ
k) dE d
ˆ
kδ
E − E
δ
ˆ
k−
ˆ
k
.
(54.222)
On integrating (54.222) over all E and
ˆ
k for a single
particle distributed over all |E,
ˆ
k states, N
and ρ are
then interrelated by
N
2
ρ
E,
ˆ
k
=mp/h
3
. (54.223)
The incident current is
j dE d
ˆ
k
e
= v
N
2
ρ(E,
ˆ
k) dE d
ˆ
k
e
(54.224a)
=
2mE/h
3
dE d
ˆ
k
e
=v dp
e
/h
3
.
(54.224b)
Radial Wave Connection. From (54.210)and(54.212),
N = (4π N
/k), so that the connection between N of
(54.220)andρ(E) is
|
N
|
2
ρ(E,
ˆ
k) =
2m/
2
πk
=
(2/π)
ka
0
e
2
. (54.225)
RR Cross Sections
for Common Normalization Factors
of Continuum Radial Functions
(a)
N = 1; ρ(E) =
2m/
2
πk
=
(2/π)
(ka
0
)e
2
, (54.226)
σ
n
R
(E) =
8π
2
a
2
0
(ka
0
)
3
m
D
fi
2
d
ˆ
k
e
, (54.227)
where D
fi
of (54.204) is dimensionless.
Part D 54.8
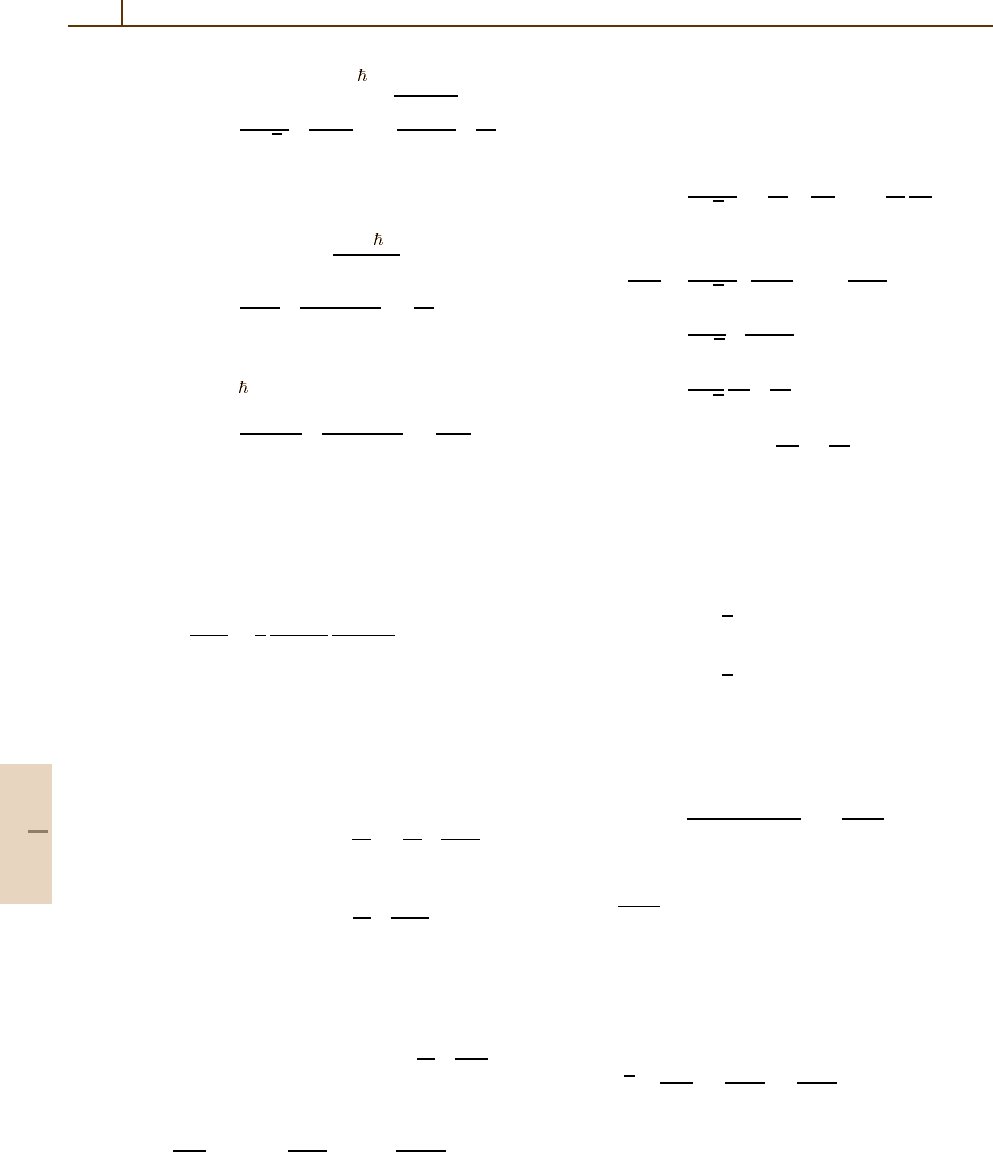
822 Part D Scattering Theory
(b)
N = k
−1
; ρ(E) =
2m/
2
(k/π) ,
(54.228)
σ
n
R
(E) =
16πa
2
0
3
√
2
αhν
e
2
/a
0
3
3
e
2
/a
0
E
R
I
a
5
0
,
(54.229)
where (54.216b)and(54.216c)forR
I
has dimen-
sion
L
5
.
(c)
N = k
−1/2
; ρ(E) =
2m/
2
π
,
(54.230)
σ
n
R
(E) =
8πa
2
0
3
α
3
(hν)
3
e
2
/a
0
2
E
R
I
a
4
0
,
(54.231)
where R
I
has dimensions of
L
4
.
(d)
N =
2m/
2
π
2
E
1/4
; ρ(E) =1 , (54.232)
σ
n
R
(E) =
4(πa
0
)
2
3
α
3
(hν)
3
e
2
/a
0
2
E
R
I
e
2
a
0
,
(54.233)
where R
I
has dimensions of
L
2
E
−1
.
54.8.4 Bound-Free Oscillator Strengths
For a transition n → E to E + dE,
d f
n
dE
=
2
3
(hν)
(e
2
/a
0
)
1
(2 +1)
m
m
r
ε
m
nm
2
,
(54.234)
R
I
(ε;n) =
d
ˆ
k
e
m
|
Ψ
nm
|r|Ψ
i
(k
e
)
E
|
2
=
m,
,m
r
ε
m
nm
2
, (54.235)
σ
n
R
(E) = 2π
2
αa
2
0
g
A
k
2
ν
k
2
e
e
2
a
0
d f
n
dE
,
(54.236a)
σ
n
I
(hν) =2π
2
αa
2
0
g
+
A
e
2
a
0
d f
n
dE
.
(54.236b)
Semiclassical Hydrogenic Systems
g
A
= g
n
=2(2 +1), g
+
A
=1 ,
σ
n
R
(E) =
n−1
=0
σ
n
R
(E) = 2π
2
αa
2
0
k
2
ν
k
2
e
dF
n
dE
,
(54.237)
dF
n
dE
=
n−1
=0
g
n
d f
n
dE
= 2
,m
d f
nm
dE
.
(54.238)
Bound–Bound Absorption Oscillator Strength. For
a transition n →n
,
F
nn
=2
m
m
f
n
m
nm
(54.239a)
=
2
6
3
√
3π
4
1
n
2
−
1
n
2
−3
5
1
n
3
1
n
3
,
(54.239b)
dF
n
dE
=
2
5
3
√
3π
n
I
2
n
(hν)
3
=2n
2
d f
n
dE
,
(54.239c)
σ
n
R
(E) =
2
5
α
3
3
√
3
nI
2
n
E(hν)
πa
2
0
, (54.239d)
σ
n
I
(hν) =
2
6
α
3
√
3
n
Z
2
I
n
hν
3
πa
2
0
, (54.239e)
=7.907 071
n
Z
2
I
n
hν
3
Mb . (54.239f)
This semiclassical analysis yields exactly Kramers
PI and associated RR cross sections in Sect. 54.8.2.
54.8.5 Radiative Recombination Rate
ˆ
α
n
R
(T
e
) =v
e
∞
0
εσ
n
R
(ε) e
−ε
dε (54.240a)
≡v
e
-
σ
n
R
(T
e
)
.
, (54.240b)
where ε = E/k
B
T and
σ
n
R
(T
e
)
is the Maxwellian-
averaged cross section for radiative recombination.
In terms of the continuum-bound A
n
(E),
ˆ
α
n
R
(T
e
) =
h
3
(2πm
e
k
B
T )
3/2
∞
0
dA
n
dε
e
−ε
dε,
(54.241)
dA
n
dE
=ρ(E)
m
A
nm
(E,
ˆ
k
e
) d
ˆ
k
e
. (54.242)
Milne Detailed Balance Relation
In terms of σ
n
I
(hν),
ˆ
α
n
R
(T
e
)
=
v
e
g
A
2g
+
A
k
B
T
e
mc
2
I
n
k
B
T
e
2
-
σ
n
I
(T
e
)
.
,
(54.243)
where, in reduced units ω = hν/I
n
, T =k
B
T
e
/I
n
=b
−1
n
,
the averaged PI cross section corresponding to (54.174)
Part D 54.8
Electron–Ion and Ion–Ion Recombination 54.8 Radiative Recombination 823
is
-
σ
n
I
(T )
.
=
e
1/T
T
∞
1
ω
2
σ
n
I
(ω) e
−ω/T
dω. (54.244)
When σ
n
I
(ω) isexpressedinMb
10
−18
cm
2
,
ˆ
α
n
R
(T
e
) =1.508×10
−13
300
T
e
1/2
I
n
I
H
2
g
A
2g
+
A
×
-
σ
n
I
(T)
.
cm
3
s
−1
. (54.245)
When σ
I
can be expressed in terms of the threshold cross
section σ
n
0
(54.178)as
σ
n
I
(hν) =(I
n
/hν)
p
σ
0
(n);( p = 0, 1, 2, 3),
(54.246)
then
σ
n
I
(T)
= S
p
(T )σ
0
(n),where
S
0
(T ) = 1 +2T +2T
2
, S
1
(T ) = 1 +T ,
(54.247a)
S
2
(T ) = 1 , (54.247b)
S
3
(T ) =
e
1/T
/T
E
1
(1/T ) (54.247c)
T1
∼ 1 −T +2T
2
−6T
3
. (54.247d)
The case p = 3 corresponds to Kramers PI cross section
(54.181)sothat
K
ˆ
α
n
R
(T
e
) =
(2 +1)
n
2
2
n
ˆ
α
0
(T
e
)S
3
(T ) (54.248a)
≡
K
ˆ
α
n
R
(T
e
→0)S
3
(T ), (54.248b)
such that
K
ˆ
α
n
R
∼ Z
2
/
n
3
T
1/2
e
as T =(k
B
T
e
/I
n
) →0.
54.8.6 Gaunt Factor, Cross Sections
and Rates for Hydrogenic Systems
The Gaunt factor G
n
is the ratio of the quantal to
Kramers (K) semiclassical PI cross section such that
σ
n
I
(hν) =
K
σ
n
I
(hν)G
n
(ω) ; (54.249)
ω = hν/I
n
=1+E/I
n
.
(a) Radiative Recombination Cross Section
σ
n
R
(E) =
g
A
g
+
A
α
2
(hν)
2
2E(e
2
/a
0
)
G
n
(ω)
K
σ
n
I
(hν)
(54.250a)
= G
n
(ω)
K
σ
n
R
(E) (54.250b)
=
(2 +1)
n
2
G
n
(ω)
K
σ
n
R
(E), (54.250c)
σ
n
R
(E) = G
n
(ω)
K
σ
n
R
(E) (54.250d)
where the quantum mechanical correction, or Gaunt
factor, to the semiclassical cross sections
G
n
(ω) →
1,ω→1
ω
−(+1/2)
,ω→∞
(54.251)
favors low n states. The -averaged Gaunt factor is
G
n
(ω) =
1/n
2
n−1
=0
(2 +1)G
n
(ω) . (54.252)
Approximations for G
n
:asε increases from zero,
G
n
(ε) =
1+
4
3
(a
n
+b
n
) +
28
18
a
2
n
−3/4
(54.253a)
1−(a
n
+b
n
) +
7
3
a
n
b
n
+
7
6
b
2
n
(54.253b)
where E = ε
Z
2
e
2
/2a
0
, ω =1+n
2
ε,and
a
n
(ε) =0.172 825
1−n
2
ε
c
n
(ε) , (54.254a)
b
n
(ε) =0.049 59
1+
4
3
n
2
ε +n
4
ε
2
c
2
n
(ε) ,
(54.254b)
c
n
(ε) =n
−2/3
1+n
2
ε
−2/3
. (54.254c)
Radiative Recombination Rate
ˆ
α
n
R
(T
e
) =
K
ˆ
α
n
R
(T
e
→0)F
n
(T ),
(54.255)
ˆ
α
n
R
(T
e
→0) =
(2 +1)
n
2
2
n
ˆ
α
0
(T
e
), (54.256)
in accordance with (54.185b).
F
n
(T ) =
e
1/T
T
∞
1
G
n
(ω)
ω
e
−ω/T
dω. (54.257)
The multiplicative factors F and G convert the semi-
classical (Kramers) T
e
→ 0 rate and cross section to
their quantal values. Departures from the scaling rule
Z
2
/n
3
T
1/2
e
for RR rates is measured by F
n
(T ).
54.8.7 Exact Universal Rate Scaling Law
and Results for Hydrogenic Systems
ˆ
α
n
R
(Z, T
e
) = Z
ˆ
α
n
R
1, T
e
/Z
2
(54.258)
as exhibited by (54.243) with (54.239e)and(54.244).
Recombination rates are greatest into low n levels
and the ω
−−1/2
variation of G
n
preferentially popu-
lates states with low ≈2–5. Highly accurate analytical
Part D 54.8
824 Part D Scattering Theory
fits for G
n
(ω) have been obtained for n ≤ 20 so
that (54.249) can be expressed in terms of known
functions of fit parameters [54.17]. This procedure
(which does not violate the S
2
sum rule) has been ex-
tended to nonhydrogenic systems of neon-like Fe XVII,
where σ
n
I
(ω) is a monotonically decreasing function
of ω.
The variation of the -averaged values
n
−2
n−1
=0
(2 +1)F
n
(T )
is close in both shape and magnitude to the correspond-
ing semiclassical function S
3
(T ),givenby(54.257) with
G
n
(ω) =1. Hence the -averaged recombination rate is
ˆ
α
n
R
(Z, T ) = (300/T )
1/2
Z
2
/n
F
n
(T )
×1.1932 × 10
−12
cm
3
s
−1
,
where F
n
can be calculated directly from (54.257)or
be approximated as G
n
(1)S(T ). A computer program
based on a three-term expansion of G
n
is also avail-
able [54.18]. From a three-term expansion for G,therate
of radiative recombination into all levels of a hydrogenic
system is
ˆ
α(Z, T ) =5.2×10
−14
Zλ
1/2
×
0.43+
1
2
ln λ +0.47/λ
1/2
,
(54.259)
where λ = 1.58×10
5
Z
2
/T and [
ˆ
α]=cm
3
/s. Tables
[54.19] exist for the effective rate
ˆ
α
n
E
(T ) =
∞
n
=n
n
−1
=0
ˆ
α
n
R
C
n
,n
(54.260)
of populating a given level n of H via radiative recom-
bination into all levels n
≥n with subsequent radiative
cascade (i → f ) with probability C
i, f
via all possible
intermediate paths. Tables [54.19]alsoexistforthefull
rate
ˆ
α
N
F
(T ) =
∞
n=N
n−1
=0
ˆ
α
n
R
(54.261)
of recombination, into all levels above N =1, 2, 3, 4, of
hydrogen. They are useful in deducing time scales of
radiative recombination and rates for complex ions.
54.9 Useful Quantities
(a) Mean Speed
v
e
=
8k
B
T
πm
e
1/2
=1.076 042 × 10
7
T
300
1/2
cm/s
=6.692 38 × 10
7
T
1/2
eV
cm/s
v
i
=2.511 16 × 10
5
T
300
1/2
m
p
/m
i
1/2
cm/s
where (m
p
/m
e
)
1/2
= 42.850 352, and T = 11 604.45 T
eV
relates the temperature in K and in eV.
(b) Natural Radius
|V(R
e
)|=e
2
/R
e
=k
B
T .
R
e
=
e
2
k
B
T
=557
300
T
Å =
14.4
T
eV
Å .
(c) Boltzmann Average Momentum
p
=
∞
−∞
e
−p
2
/2mk
B
T
dp = (2πm
e
k
B
T )
1/2
.
(d) De Broglie Wavelength
λ
dB
=
h
p
=
h
(2πm
e
k
B
T )
1/2
=
7.453 818 × 10
−6
T
1/2
e
cm
=43.035
300
T
e
1/2
Å =
6.9194
T
1/2
eV
Å .
References
54.1 J. Stevefelt, J. Boulmer, J-F. Delpech: Phys. Rev. A
12, 1246 (1975)
54.2 R. Deloche, P. Monchicourt, M. Cheret, F. Lambert:
Phys. Rev. A 13, 1140 (1976)
54.3 P. Mansbach, J. Keck: Phys. Rev. 181, 275 (1965)
54.4 L. P. Pitaevski
˘
ı: Sov. Phys. JETP 15,919(1962)
54.5 H. A. Kramers: Philos. Mag. 46, 836 (1923)
54.6 D. R. Bates: Phys. Rev. 78, 492 (1950)
Part D 54
