Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics

Подождите немного. Документ загружается.

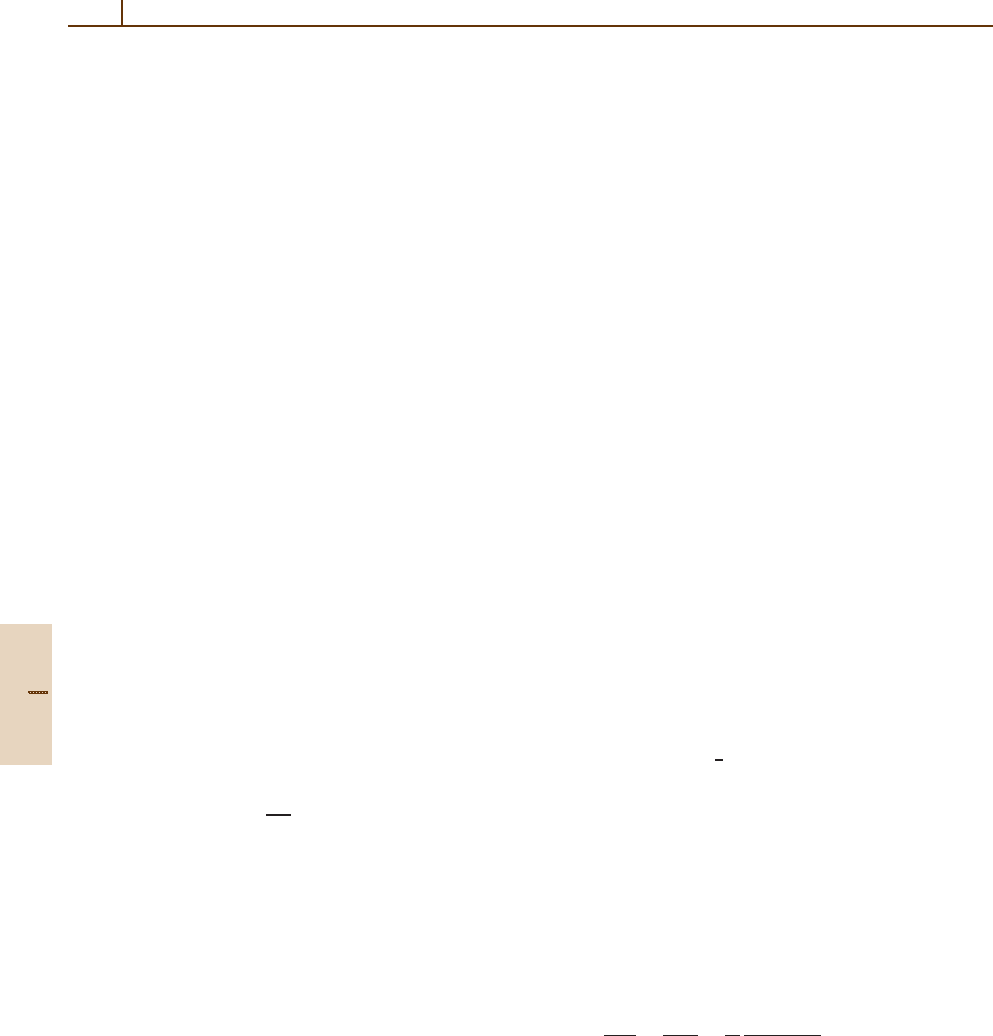
794 Part D Scattering Theory

from isotropic inital states are distributed symmetrically

about this axis, i. e., about 90

◦

, in ﬁrst approxima-

tion. Because q is averaged over in forming the cross

section, all directions contribute to some extent, and

the distribution is not completely symmetric. The solid

curve in Fig. 53.3 represents a distribution computed

in the Bethe–Born approximation, and it is seen to

peak at 90

◦

but is somewhat asymmeteric about this

angle, reﬂecting effects of averaging over the direc-

tion of q. Such distributions are well described by

only a few partial waves for the outgoing electron. In-

deed, the theoretical distribution is well described by

a combination of s and p waves. The calculations ﬁt

the experimental data except in the forward direction

where the experimental distribution increases sharply.

Such sharp increases must reﬂect the presence of many

partial waves not described by the Born approximation.

Since the main disagreement between theory and ex-

periment is conﬁned to a small angular region near

◦

which contributes only a small part to the total

cross section, the Bethe–Born approximation represents

a well-founded theoretical framework for interpreting

features that appear in the low-electron-energy portion

of the DDCS.

While the main contribution to total ionization cross

sections comes from the low energy region, electrons

in the high energy region (v/2 < k) carry more energy

per electron, and therefore play a prominent role in pro-

cesses initiated by fast electrons. The fast electrons on

the Bethe ridge correspond to collisions where the mo-

mentum q lost by the incident projectile is transferred

mainly to the ejected electron. Because the momen-

tum k of the ejected electrons is much larger than the

mean value of the electron momentum in the initial

state, given by

√

2ε

, this portion of the spectrum can

be interpreted in terms of a binary collision between

the incident projectile and the target electron treated as

quasifree. By quasifree we understand that the electron

has a nonzero binding energy ε

, but is otherwise re-

garded as a free electron with an initial momentum s,

distributed over a range of values centered around the

mean value. In the projectile reference frame, the elec-

tron has the momentum s−v. The electron scatters

elastically from the projectile and emerges with a ﬁ-

nal momentum k



= k−v. This simple picture is known

as the elastic scattering model, and is often employed

for processes involving weakly bound electrons [53.11].

There are several quantal versions of this picture, indeed

any theory of ionization must reduce to the electron scat-

tering model in the limit that the initial binding energy ε

vanishes.

When the projectile P is a bare ion so that the bi-

nary scattering process is just Rutherford scattering, the

Bethe–Born approximation is in accord with this picture.

It works because the electrons are fast so that effects of

the target potential in the ﬁnal state are unimportant,

and because a ﬁrst-order computation of Rutherford

scattering gives the same scattering cross section as

the exact Rutherford amplitude. For that reason the

domain of applicability of the ﬁrst Born approxima-

tion includes the Bethe ridge, even in the high energy

region.

The binary encounter peak shows new features

when the projectile carries electrons. The target elec-

trons scatter from a partially screened ion and the

Bethe ridge reﬂects properties of the elastic scatter-

ing cross section for the complex projectile species. In

contrast to the Rutherford cross section, elastic scat-

tering cross sections for complex species may have

maxima and minima as functions of the electron en-

ergy and angle. Such features have been identiﬁed in

collisions of highly charged ions with neutral atomic

targets [53.12].

The Continuum Electron Capture Cusp

Figure 53.2 shows a sharp cusp-like structure when

the momentum of the ejected electron in the projectile

frame k



vanishes. Then the ejected electron moves with

a velocity exactly equal to the projectile velocity. For

charged projectiles, it is virtually impossible to deter-

mine whether such electron states are Rydberg states

of high principal quantum number n



, or continuum

states with E



much less than ε

.Indeed,the

physical similarity of such atomic states implies that the

cross section for electron capture to states of high n



dif-

fers from the ionization cross section near k



= 0 only

by a density of states factor. This factor is just dE



for ionization processes and dE



= Z

−3

for cap-

ture. It follows that the cross section d

σ/ dE



dΩ



is a smooth function of E



which is nonzero and ﬁ-

nite at E



= 0. The Galilean invariant cross section

of Fig. 53.2, however, is not smooth; rather it is given



dΩ



. (53.24)

Since d

σ/ dE



dΩ



is nonzero at k



=0, it follows that

the DDCS has a k



−1

singularity at k



= 0. Experiments

measure cross sections averaged over this singular fac-

tor. The averaging results in the cusp-shaped feature at



= 0 seen in Fig. 53.2 [53.13–15].

Part D 53.2

Ionization in High Energy Ion–Atom Collisions 53.2 Prominent Features 795

The theoretical description of the cusp feature re-

quires that the electron in the ﬁnal state move mainly

in the ﬁeld of the projectile rather than that of the tar-

get. While the appropriate ﬁnal state wave function can

be introduced into (53.4), the result is quantitatively in-

accurate. A more accurate amplitude emerges when the

exact amplitude is expanded in powers the interaction

potential V

of the electron with the ﬁnal state target

ion [53.16], since V

has a much smaller effect than the

interaction V

. Approximate evaluation of the ioniza-

tion amplitude in an independent particle approximation

gives [53.17]



(J+s)

(s)

× ψ

−



(r)|exp[i(J+s)]|ψ

s−v

(r) , (53.25)

and

dΩ

= (2π)



dΩ

(53.26)

where µ is the reduced mass given by

µ = M

+1)/(M

+1), (53.27)

and

(s) is the momentum space independent-particle

orbital wave function for the active electron in the in-

tial state,

is the corresponding effective interaction

potential, and the ψ



are normalized on the momentum

scale.

Figure 53.4 gives a pictorial interpretation of this

amplitude. The initial momentum distribtution of the

electron is given by

(s). In the projectile frame,

this electron has momentum s −v and moves in

a projectile continuum state represented by ψ

s−v

(r).

Owing to the interaction with the target represented by

exp[i(J +s)]

(J+s), a transition to the ﬁnal projec-

tile state ψ

−



occurs as illustrated in Fig. 53.4 (b). The

ﬁnal state ψ

−



has a 1/

√



normalization that gives rise

to the cusp at k = v seen in Fig. 53.2. This picture de-

scribes ionization in terms of the free–free transition,

−

s−v

→ ψ



The amplitude in (53.25), known as the dis-

torted wave strong potential Born amplitude (DSPB)

[53.18], or the projectile impulse approximation ampli-

tude [53.19], also describes binary encounter electrons.

Thus the regions of applicability of (53.4)and(53.25)

overlap considerably. In the binary encounter region,

where k



>v/2andJ ≈0, the cross section given by

(53.9)and(53.25) reduces to the elastic scattering model

(ESM) [53.20], where the incident electron with projec-

tile frame momentum −J−v quasi-elastically scatters

–

s-v

(s-v)

–

(J + s)e

–i(J+ S)r

Fig. 53.4a,b Free–free transition picture of ionization.

(a) Schematic representation of a target electron with mo-

mentum s−v in the projectile frame.

(b) A free–free

transition from the projectile eigenstate ψ

−

s−v

to the ﬁ-

nal eigenstate ψ



occurs with the target interaction as the

transition operator

from the projectile into a ﬁnal state with projectile

frame momentum k



. This quasi-elastic cross section

is averaged over the initial momentum distribution of

the electron |

(−J)|

J so that

ESM



(2π)



elas



, −J−v)|

|dΩ





× |

(−J)|

J . (53.28)

The projectile frame cross section is recovered

upon using the relation d

J = µ

v dΩ



(53.25).

The two approximations (53.4)and(53.25) describe

all of the major features that emerge in the ioniza-

tion of one-electron targets by fully ionized projectiles.

Both theories also incorporate some multi-electron ef-

fects that appear when either the target or projectile

(or both) have several electrons. Equation (53.28)is

useful for describing effects of target ionization by

multi-electron projectiles when the projectile electrons

remain in their ground state since T

elas

incorporates,

in principle, the exact amplitude for electrons to scat-

ter from the projectile in its ground state. Of course,

the multi-electron projectile can also become excited

or ionized owing to its interaction with the target elec-

trons. These processes are not incorporated in the ESM

cross section (53.28); rather the Born amplitude of

(53.4) represents a more tractable theory to analyze these

features.

Part D 53.2

796 Part D Scattering Theory

53.2.2 Projectile Electrons

When the incident atomic species carries some attached

electrons, these electrons may be removed in the col-

lision with a target. Essentially all of the features that

appear for the target electrons also appear for the pro-

jectile electrons; however the DDCS is shifted by the

Galilean transformation to the projectile frame. The

transformation from the laboratory frame to the projec-

tile frame is an essential step for interpreting features of

the projectile electrons. This transformation has the ef-

fect of spreading out the electron energy distribution

since at θ

= 0

◦

a small energy interval ∆E

in the

lab frame relates to a small energy interval ∆ E



in the

projectile frame according to

∆E

= ∆E





1 +

√

2vE





(53.29)

For example, when the projectile energy is 1.5MeV/au,

a projectile frame electron energy interval 0 < E



0.1 eV maps into an interval of ±8.3 eV centered at

= 817 eV. This ampliﬁcation of both the electron en-

ergy and the electron energy interval proves useful for

measuring features of projectile species with high reso-

lution [53.21].

53.3 Recent Developments

Added by Mark M. Cassar. The theoretical study of ion-

ization processes in atomic collisions remains an active

research ﬁeld. At present, there are three main quantum

mechanical approaches to the simplest colliding sys-

tems with one active electron. The ﬁrst approach is to

solve directly the time-dependent Schrödinger equation

by taking advantage of modern-day computing power.

The accuracy of these calculations, however, is still in-

sufﬁcient, and further computational and technological

advancements are necessary. The second approach ex-

pands the total wave function in atomic or molecular

bases; satisfactory agreement with experimental results

is obtained, but at the expense of having to include a large

number of basis set members in the expansions. The

third approach involves the use of Sturmian expansions,

along with a speciﬁc scaling and transformation of the

wave functions. This technique overcomes many of the

difﬁculties that others suffer from, and at the same time

provides the best agreement with experimental data over

a broad range of energies.

Problems in our understanding of the ionization pro-

cess remain, even for the simplest colliding system

-H, and extensions and reﬁnements of the present

theoretical and experimental methods are needed.

The reader is referred to the in-depth review by

Macek et al. [53.22].

References

53.1 U. Fano: Ann. Revs. Nucl. Sci. 13,1(1963)

53.2 J. S. Briggs, K. Taulbjerg: Theory of inelastic atom–

atom collisions. In: Structure and Collisions in Ions

and Atoms, ed. by I. A. Sellin (Springer, Berlin,

Heidelberg 1978) pp. 105–153

53.3 H. A. Bethe, E. E. Salpeter: Quantum Mechanics of

One- and Two-Electron Atoms (Plenum, New York

1977)

53.4 M. Inokuti: Rev. Mod. Phys. 43, 297 (1971)

53.5 S. Geltman: Topics in Atomic Collision Theory (Aca-

demic, New York 1969) pp. 41–44

53.6 F. Drepper, J. S. Briggs: J. Phys. B 9, 2063 (1976)

53.7 A. F. Starace: Theory of atomic photoionization. In:

Handbuch der Physik,Vol.31,ed.byW.Mehlhorn

(Springer, Berlin, Heidelberg 1982)

53.8 S. T. Manson, L. H. Toburen: Phys. Rev. Lett. 46,529

(1981)

53.9 H. M. Hartley, H. R. J. Walters: J. Phys. B 20,1983

(1987)

53.10 S. T. Manson, L. Toburen, D. Madison, N. Stolter-

foht: Phys. Rev. A 12, 60 (1975)

53.11 M. M. Duncan, M. G. Menendez: Phys. Rev. A 16,

1799 (1977)

53.12 D. H. Lee, P. Richard, T. J. M. Zouros, J. M. Sanders,

J. L. Shinpaugh, H. Hidmi: Phys. Rev. A 41,4816

(1990)

53.13 M. E. Rudd, J. H. Macek: Case Studies in Atomic

Physics, 3, 47 (1972)

53.14 G. G. Crooks, M. E. Rudd: Phys. Rev. Lett. 25,1599

(1970)

Part D 53

Ionization in High Energy Ion–Atom Collisions References 797

53.15 K. G. Harrison, M. W. Lucas: Phys. Lett. 33 A,142

(1970)

53.16 J. S. Briggs: J. Phys. B 10, 3075 (1977)

53.17 M. Brauner, J. H. Macek: Phys. Rev. A 46,2519

(1992)

53.18 K. Taulbjerg, R. Barrachina, J. H. Macek: Phys. Rev.

A 41, 207 (1990)

53.19 D. Jakubassa-Amundsen: J. Phys. B 16,1767

(1983)

53.20 J. Macek, K. Taulbjerg: J. Phys. B 26,1353

(1993)

53.21 N. Stolterfoht: Phys. Rep. 146,315(1987)

53.22 S. Yu. Ovchinnikov, G. N. Ogurtsov, J. H. Macek,

Yu. S. Gordeev: Phys. Rep. 389, 119 (2004)

Part D 53

799

Electron–Ion a

54. Electron–Ion and Ion–Ion Recombination

Electron–ion and ion–ion recombination

processes are of key importance in under-

standing the properties of plasmas, whether

they are in the upper atmosphere, the so-

lar corona, or industrial reactors on earth.

This is a collection of formulae, expressions,

and speciﬁc equations that cover the vari-

ous aspects, approximations, and approaches

to electron-ion and ion-ion recombination

processes.

54.1 Recombination Processes ..................... 800

54.1.1 Electron–Ion Recombination ...... 800

54.1.2 Positive–Ion Negative–Ion

Recombination ......................... 800

54.1.3 Balances .................................. 800

54.2 Collisional-Radiative Recombination ..... 801

54.2.1 Saha and Boltzmann

Distributions............................. 801

54.2.2 Quasi-Steady

State Distributions..................... 802

54.2.3 Ionization and Recombination

Coefﬁcients .............................. 802

54.2.4 Working Rate Formulae.............. 802

54.3 Macroscopic Methods ........................... 803

54.3.1 Resonant Capture-Stabilization

Model: Dissociative

and Dielectronic Recombination . 803

54.3.2 Reactive Sphere Model:

Three-Body Electron–Ion

and Ion–Ion Recombination....... 804

54.3.3 Working Formulae

for Three-Body Collisional

Recombination at Low Density.... 805

54.3.4 Recombination Inﬂuenced

by Diffusional Drift at High Gas

Densities .................................. 806

54.4 Dissociative Recombination .................. 807

54.4.1 Curve-Crossing Mechanisms........ 807

54.4.2 Quantal Cross Section................. 808

54.4.3 Noncrossing Mechanism............. 810

54.5 Mutual Neutralization .......................... 810

54.5.1 Landau–Zener Probability

for Single Crossing at R

............. 811

54.5.2 Cross Section and Rate Coefﬁcient

for Mutual Neutralization ........... 811

54.6 One-Way Microscopic Equilibrium

Current, Flux, and Pair-Distributions..... 811

54.7 Microscopic Methods for Termolecular

Ion–Ion Recombination ....................... 812

54.7.1 Time Dependent Method:

Low Gas Density ........................ 813

54.7.2 Time Independent Methods:

Low Gas Density ........................ 814

54.7.3 Recombination at Higher Gas

Densities .................................. 815

54.7.4 Master Equations ...................... 816

54.7.5 Recombination Rate .................. 816

54.8 Radiative Recombination ..................... 817

54.8.1 Detailed Balance

and Recombination-Ionization

Cross Sections ........................... 817

54.8.2 Kramers Cross Sections, Rates,

Electron Energy-Loss Rates

and Radiated Power

for Hydrogenic Systems .............. 818

54.8.3 Basic Formulae for Quantal Cross

Sections ................................... 819

54.8.4 Bound-Free Oscillator Strengths.. 822

54.8.5 Radiative Recombination Rate .... 822

54.8.6 Gaunt Factor, Cross Sections

and Rates for Hydrogenic

Systems ................................... 823

54.8.7 Exact Universal Rate Scaling Law

and Results for Hydrogenic

Systems ................................... 823

54.9 Useful Quantities ................................. 824

References .................................................. 824

Part D 54

800 Part D Scattering Theory

54.1 Recombination Processes

54.1.1 Electron–Ion Recombination

This proceeds via the following four processes:

(a) radiative recombination (RR)

−

+ A

(i) → A(n) +hν, (54.1)

(b) three-body collisional-radiative recombination

−

+ A

+ e

−

→ A + e

−

, (54.2a)

−

+ A

+M → A + M , (54.2b)

where the third body can be an electron or a neutral gas.

−

+ A

Z+

(i) 



Z+

(k) − e

−



n

→ A

(Z−1)+







( f ) +hν, (54.3)

(d) dissociative recombination (DR)

−

+ AB

→ A +B

∗

. (54.4)

Electron recombination with bare ions can proceed

only via (a) and (b), while (c) and (d) provide additional

pathways for ions with at least one electron initially

or for molecular ions AB

. Electron radiative capture

denotes the combined effect of RR and DLR.

54.1.2 Positive–Ion Negative–Ion

Recombination

This proceeds via the following three processes:

(e) mutual neutralization

−

→ A +B

∗

, (54.5)

(f) three-body (termolecular) recombination

−

+M → AB +M , (54.6)

(g) tidal recombination

−

+M → AC +B + M (54.7a)

→ BC + A +M , (54.7b)

where M is some third species (atomic, molecular or

ionic). Although (e) always occurs when no gas M is

present, it is greatly enhanced by coupling to (f). The

dependence of the rate

α on density N of background

gas M is different for all three cases, (e)–(g).

Processes (a), (c), (d) and (e) are elementary pro-

cesses in that microscopic detailed balance (proper

balance) exists with their true inverses, i. e., with pho-

toionization (both with and without autoionization) as

in (c) and (a), associative ionization and ion-pair for-

mation as in (d) and (e), respectively. Processes (b), (f)

and (g) in general involve a complex sequence of elem-

entary energy-changing mechanisms as collisional and

radiative cascade and their overall rates are determined

by an input-output continuity equation involving micro-

scopic continuum-bound and bound–bound collisional

and radiative rates.

54.1.3 Balances

Proper Balances

Proper balances are detailed microscopic balances be-

tween forward and reverse mechanisms that are direct

inverses of one another, as in

(a) Maxwellian: e

−

) + e

−

)  e

−



) + e

−



(54.8)

where the kinetic energy of the particles is redistributed;

(b) Saha: e

−

+H(n)  e

−

+ e

−

(54.9)

between direct ionization from and direct recombination

into a given level n;

−

+H(n)  e

−

+H(n



,



) (54.10)

between excitation and de-excitation among bound

levels;

(d) Planck: e

−

 H(n) +hν, (54.11)

which involves interaction between radiation and atoms

in photoionization/recombination to a given level n.

Improper Balances

Improper balances maintain constant densities via pro-

duction and destruction mechanisms that are not pure

inverses of each other. They are associated with ﬂux

activity on a macroscopic level as in the transport of

particles into the system for recombination and net

production and transport of particles (i. e. e

−

, A

)for

ionization. Improper balances can then exist between

dissimilar elementary production–depletion processes

as in (a) coronal balance between electron-excitation

into and radiative decay out of level n. (b) radiative

Part D 54.1

Electron–Ion and Ion–Ion Recombination 54.2 Collisional-Radiative Recombination 801

balance between radiative capture into and radiative cas-

cade out of level n. (c) excitation saturation balance

between upward collisional excitations n−1 →n →n+

1 between adjacent levels. (d) de-excitation saturation

balance between downward collisional de-excitations

n+1 →n → n−1 into and out of level n.

54.2 Collisional-Radiative Recombination

Radiative Recombination

Process (54.1) involves a free-bound electronic tran-

sition with radiation spread over the recombination

continuum. It is the inverse of photoionization without

autoionization and favors high energy gaps with tran-

sitions to low n ≈ 1, 2, 3 and low angular momentum

states  ≈0, 1, 2 at higher electron energies.

Three-Body Electron–Ion Recombination

Processes (54.2a,b) favor free-bound collisional tran-

sitions to high levels n, within a few k

T of the

ionization limit of A(n) and collisional transitions

across small energy gaps. Recombination becomes sta-

bilized by collisional-radiative cascade through the

lower bound levels of A. Collisions of the e

−

−A

pair with third bodies becomes more important for

higher levels n and radiative emission is important

down to and among the lower levels n. In optically

thin plasmas this radiation is lost, while in optically

thick plasmas it may be re-absorbed. At low electron

densities radiative recombination dominates with pre-

dominant transitions taking place to the ground level.

For process (54.2a) at high electron densities, three-

body collisions into high Rydberg levels dominate,

followed by cascade which is collision dominated at

low electron temperatures T

and radiation dominated

at high T

. For process (54.2b) at low gas densities N,

the recombination is collisionally-radiatively controlled

while, at high N, it eventually becomes controlled

by the rate of diffusional drift (54.61) through the

gas M.

Collisional-Radiative Recombination

Here the cascade collisions and radiation are coupled

via the continuity equation. The population n

of an

individual excited level i of energy E

is determined by

the rate equations

∂n

∂t

+∇· (n

) (54.12)



i= f



−n



= P

−n

, (54.13)

which involve temporal and spatial relaxation in (54.12)

and collisional-radiative production rates P

and destruc-

tion frequencies D

of the elementary processes included

in (54.13). The total collisional and radiative transition

frequency between levels i and f is ν

and the f -sum

is taken over all discrete and continuous (c) states of the

recombining species. The transition frequency ν

in-

cludes all contributing elementary processes that directly

link states i and f , e.g., collisional excitation and de-

excitation, ionization (i →c) and recombination (c →i)

by electrons and heavy particles, radiative recombin-

ation (c →i), radiative decay (i → f ), possibly radiative

absorption for optically thick plasmas, autoionization

and dielectronic recombination.

Production Rates and Processes

The production rate for a level i is



f =i



f>i







+β



(54.14)

where the terms in the above order represent (1) col-

lisional excitation and de-excitation by e

−

–A( f )

collisions, (2) three-body e

−

–A

collisional recom-

bination into level i, (3) spontaneous and stimulated

radiative cascade, and (4) spontaneous and stimulated

radiative recombination.

Destruction Rates and Processes

The destruction rate for a level i is

= n



f =i



f<i







f>i

, (54.15)

where the terms in the above order represent

(1) collisional destruction, (2) collisional ionization,

Part D 54.2

802 Part D Scattering Theory

(3) spontantaneous and stimulated emission, (4) photo-

excitation, and (5) photoionization.

54.2.1 Saha and Boltzmann Distributions

Collisions of A(n) with third bodies such as e

−

and M

are more rapid than radiative decay above a certain

excited level n

∗

. Since each collision process is ac-

companied by its exact inverse the principle of detailed

balance determines the population of levels i > n

∗

Saha Distribution

This connects equilibrium densities

and

bound levels i, of free electrons at temperature T

and

of ions by



g(i )



(2πm

)

3/2

exp(I

(54.16)

where the electronic statistical weights of the free elec-

tron, the ion of charge Z +1 and the recombined e

−

−A

species of net charge Z and ionization potential I

are

= 2, g

and g(i), respectively. Since n

≤

for

all i, then the Saha–Boltzmann distributions imply that

 n

and n

 n

for i = 1, 2, where i = 1isthe

ground state.

Boltzmann Distribution

This connects the equilibrium populations of bound

levels i of energy E

[

g(i )/g( j )

]

exp



−(E

−E

)/k



(54.17)

54.2.2 Quasi-Steady State Distributions

The reciprocal lifetime of level i is the sum of radia-

tive and collisional components and is therefore shorter

than the pure radiative lifetime τ

≈ 10

−7

−4

s. The

lifetime τ

for the ground level is collisionally con-

trolled, is dependent upon n

, and generally is within

the range of 10

and 10

s for most laboratory plasmas

and the solar atmosphere. The excited level lifetimes τ

are then much shorter than τ

. The (spatial) diffusion

or plasma decay (recombination) time is then much

longer than τ

and the total number of recombined

species is much smaller than the ground-state popu-

lation n

. The recombination proceeds on a timescale

much longer than the time for population/destruction of

the excited levels. The condition for quasisteady state, or

QSS-condition, dn

/dt = 0 for the bound levels i = 1,

therefore holds. The QSS distributions n

therefore sat-

isfy P

54.2.3 Ionization and Recombination

Coefﬁcients

Under QSS, the continuity equation (54.13) then reduces

to a ﬁnite set of simultaneous equations P

.This

gives a matrix equation which is solved numerically for

(i = 1) ≤

in terms of n

and n

. The net ground-

state population frequency per unit volume (cm

−3

−1

)

can then be expressed as

−n

, (54.18)

where

and S

, respectively, are the overall rate

coefﬁcients for recombination and ionization via the

collisional-radiative sequence. The determined

equals the direct (c → 1) recombination to the ground

level supplemented by the net collisional-radiative cas-

cade from that portion of bound-state population which

originated from the continuum. The determined S

equals direct depletion (excitation and ionization) of the

ground state reduced by the de-excitation collisional ra-

diative cascade from that portion of the bound levels

accessed originally from the ground level. At low n

and S

reduce, respectively, to the radiative re-

combination coefﬁcient summed over all levels and to

the collisional ionization coefﬁcient for the ground level.

C, E and  Blocks of Energy Levels

For the recombination processes (54.2a), (54.2b)and

(54.6) which involve a sequence of elementary reac-

tions, the e

−

− A

or A

−B

−

continuum levels and

the ground A(n = 1) or the lowest vibrational levels of

AB are therefore treated as two large particle reservoirs

of reactants and products. These two reservoirs act as

reactant and as sink blocks C and  which are, respec-

tively, drained and ﬁlled at the same rate via a conduit

of highly excited levels which comprise an intermediate

block of levels E .ThisC draining and  ﬁlling pro-

ceeds, via block E , on a timescale large compared with

the short time for a small amount from the reservoirs to

be re-distributed within block E . This forms the basis of

QSS.

54.2.4 Working Rate Formulae

For electron–atomic–ion collisional-radiative recombin-

ation (54.2a), detailed QSS calculations can be ﬁtted by

Part D 54.2

Electron–Ion and Ion–Ion Recombination 54.3 Macroscopic Methods 803

the rate [54.1]



3.8×10

−9

−4.5

+1.55× 10

−10

−0.63

+6×10

−9

−2.18

0.37



−1

(54.19)

agrees with experiment for a Lyman α optically thick

plasma with n

and T

in the range 10

−3

≤ n

≤

−3

and 2.5K≤ T

≤ 4000 K. The ﬁrst term is

the pure collisional rate (54.49), the second term is the

radiative cascade contribution, and the third term arises

from collisional-radiative coupling.

For



−

−He



recombination in a high (5–

100 Torr) pressure helium afterglow the rate for (54.2b)

is [54.2]



(4±0.5) ×10

−20



(

/293

)

−(4±0.5)



(5±1) ×10

−27

n(He)

+(2.5±2.5) ×10

−10



(

/293

)

−(1±1)

/s. (54.20)

The ﬁrst two terms are in accord with the purely colli-

sional rates (54.49)and(54.52b), respectively.

54.3 Macroscopic Methods

54.3.1 Resonant Capture-Stabilization

Model: Dissociative and Dielectronic

Recombination

The electron is captured dielectronically (54.41)intoan

energy-resonant long-lived intermediate collision com-

plex of super-excited states d which can autoionize or be

stabilized irreversibly into the ﬁnal product channel f

either by molecular fragmentation

−

+ AB

(i)



∗∗

→ A +B

∗

, (54.21)

as in direct dissociative recombination (DR), or by

emission of radiation as in dielectronic recombination

(DLR)

−

+ A

Z+

(i)



Z+

(k) − e

−



n

→ A

(Z−1)+







( f ) +hν. (54.22)

Production Rate of Super-Excited States d

∗

(d) −n

∗

[

(d) +ν

(d)

]

;(54.23)

(d) =





(d →i



), (54.24a)

(d) =





(d → f



). (54.24b)

Steady-State Distribution

For a steady-state distribution, the capture volume is

∗

(d)

(d) +ν

(d)

(54.25)

Recombination Rate

and Stabilization Probability

The recombination rate to channel f is





(d)ν

(d → f )

(d) +ν

(d)



(54.26a)

and the rate to all product channels is

α =



(d)ν

(d)

(d) +ν

(d)

(54.26b)

In the above, the quantities

(d) =ν

(d → f )/

[

(d) +ν

(d)

]

, (54.27)

(d) =ν

(d)/

[

(d) +ν

(d)

]

, (54.28)

represent the corresponding stabilization probabilities.

Macroscopic Detailed Balance

and Saha Distribution

(T ) =

∗

(d)

(d →i)

= k

(d)τ

(d →i)

(54.29a)

(2πm

T )

3/2



ω(d)

2ω



×exp



−E

∗



, (54.29b)

where E

∗

is the energy of super-excited neutral levels

∗∗

above that for ion level AB

(i),andω are the

corresponding statistical weights.

Alternative Rate Formula





(d →i)ν

(d → f )

(d) +ν

(d)



(54.30)

Part D 54.3

804 Part D Scattering Theory

Normalized Excited State Distributions

∗

(d →i)

[

(d) +ν

(d)

]

(54.31)

α =



(d)P

(d) =



(d) (54.32a)



(d)

[

(d)τ

(d →i)

]

. (54.32b)

Although equivalent, (54.26a)and(54.30) are nor-

mally invoked for (54.21)and(54.22), respectively,

since P

≤ 1forDRsothat

→ k

;andν

 ν

for DLR with n  50 so that

α → K

.Forn  50,

 ν

and

α → k

. The above results (54.26a)and

(54.30) can also be derived from microscopic Breit–

Wigner scattering theory for isolated (nonoverlapping)

resonances.

54.3.2 Reactive Sphere Model:

Three-Body Electron–Ion

and Ion–Ion Recombination

Since the Coulomb attraction cannot support quasibound

levels, three body electron–ion and ion–ion recom-

bination do not in general proceed via time-delayed

resonances, but rather by reactive (energy-reducing)

collisions with the third body M. This is particularly

effective for A–B separations R ≤ R

, as in the sequence

A + B



∗

(R ≤ R

), (54.33a)

∗

(R ≤ R

) +M



−s

AB +M . (54.33b)

In contrast to (54.21)and(54.22) where the stabilization

is irreversible, the forward step in (54.33b) is reversible.

The sequence (54.33a)and(54.33b) represents a closed

system where thermodynamic equilibrium is eventually

established.

Steady State Distribution of AB

∗

Complex

∗



+ν



(t)n

(t) +



−s

+ν



(t).

(54.34)

Saha and Boltzmann balances:

Saha:

∗

Boltzmann:

−s

∗

(54.35)

∗

is in Saha balance with reactant block C and in

Boltzmann balance with product block .

Normalized Distributions

∗

= P

(t) + P

(t), (54.36a)

(t) =

(t)n

(t)

,γ

(t) =

(t)

. (54.36b)

Stabilization and Dissociation Probabilities

(ν

+ν

)

, P

(ν

+ν

)

(54.37)

Time Dependent Equations

=−k

[

(t) −γ

(t)

]

, (54.38a)

=−ν

−s

[

(t) −γ

(t)

]

, (54.38b)

=−

(t)n

(t) +k

(t). (54.39)

where the recombination rate coefﬁcient





and

dissociation frequency are, respectively,

= k

(ν

+ν

)

(54.40)

= ν

−s

(ν

+ν

)

(54.41)

which also satisfy the macroscopic detailed balance

relation

. (54.42)

Time Independent Treatment

The rate

given by the time dependent treatment can

also be deduced by viewing the recombination process

as a source block C kept fully ﬁlled with dissociated

species A and B maintained at equilibrium concentra-

tions

(i. e. γ

=1) and draining at the rate

through a steady-state intermediate block E of excited

levels into a fully absorbing sink block  of fully associ-

ated species AB kept fully depleted with γ

= 0sothat

there is no backward re-dissociation from block .The

frequency k

is deduced as if the reverse scenario, γ

and γ

= 0, holds. This picture uncouples

α and k

and allows each coefﬁcient to be calculated indepen-

dently. Both dissociation (or ionization) and association

(recombination) occur within block E.

If γ

=1andγ

=0, then

∗

=ν

/(ν

+ν

), (54.43a)

K =

∗

= k

/ν

, (54.43b)

=ν

/(ν

+ν

) =ρ

∗

, (54.43c)

Part D 54.3