Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics
Подождите немного. Документ загружается.


762 Part D Scattering Theory
adapted to cases where long range avoided crossings
are dominant [51.10]. If a semiclassical approximation
is introduced, the scattering equations become almost
identical to those obtained directly using translation
factors of the CTF (common translation factor) type
[51.11, 12].
Three representative systems are chosen to illustrate
the basic features of the problem: Al
3+
/HandB
3+
/He
which are typical of type I, and O
2+
/H which is typical
of type II. In the Al
3+
/H system, charge transfer takes
place via the reaction [51.13]
Al
3+
3s
2
2
S +H → Al
2+
3s
2
3p
2
P +H
+
(51.1)
involving a network of two Σ and one Π adiabatic states.
In the B
3+
/He system, charge exchange occurs via a net-
work of three Σ and one Π states involving two avoided
crossings [51.14]. The two possible capture channels are
B
3+
1s
2
+He → B
2+
1s
2
nl
+He
+
,
nl = 2s, 2p .
(51.2)
The O
2+
/H system is a good example of a type II reac-
tion which plays an important role in astrophysical plas-
mas [51.15, 16]. The dominant reaction at low energies
O
2+
2s
2
2p
2
3
P +H → O
+
2s2p
4
4
P +H
+
(51.3)
involves only quartet states.
51.1 Molecular Structure Calculations
The construction of the network of adiabatic states of
the molecular ion complex constitutes the first step in
analyzing the dynamics of the ion–atom system. In prin-
ciple, standard techniques of quantum chemistry can be
employed. For doubly charged ions, where type II pro-
cesses dominate and the effective avoided crossings take
place at relatively short range, ab initio methods are re-
quired. On the other hand, for trebly and more highly
charged ions, where type I processes dominate, the ef-
fective avoided crossings occur at long range where ab
initio methods can be quite inaccurate. Model potential
methods are then often more satisfactory.
51.1.1 Ab Initio Methods
Both molecular orbital and valence-bond methods have
been extensively used and (provided a sufficient number
of configurations are included) should be satisfactory
in principle. A simple test is the location of the long
range crossings, which is very sensitive to the en-
ergy difference of the initial and final channels. But
this test is insufficient. For example, in the C
3+
/H
system, for which both the molecular orbital and va-
lence bond methods yield comparable results in regions
well away from avoided crossings, there are significant
discrepancies in the important region of the avoided
acrossings [51.17, 18]. In the present state of the art,
the absolute accuracy of theoretical calculations in the
crossing region is difficult to ascertain. Of course, since
the computed electron capture cross sections depend
sensitively on the minimum energy separation, experi-
mental data at low collision energies makes some tests
possible. Unfortunately, there is not yet much reliable
data at low eV energies.
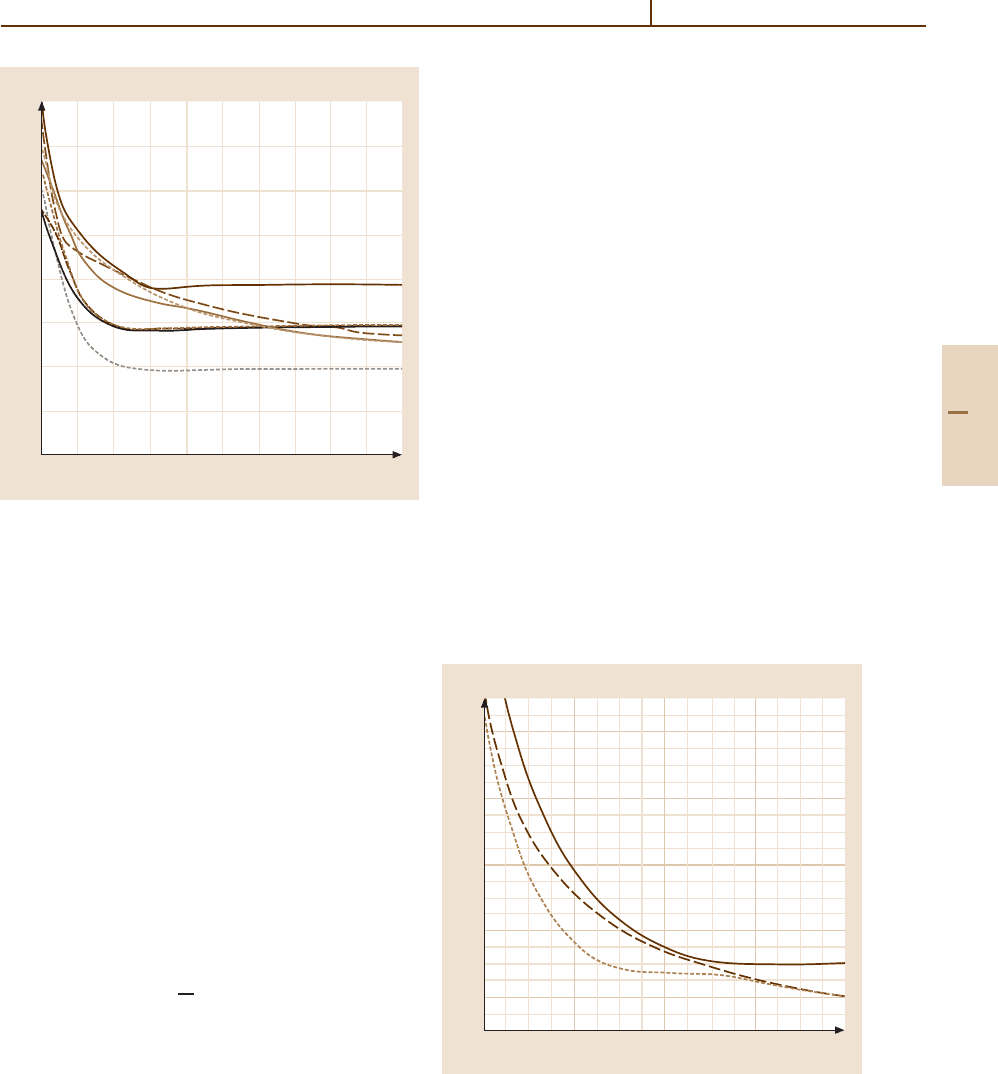
Figures 51.1 and 51.2 present the adiabatic network
of the
4
Σ
−
,
4
Π and
2
Σ
+
,
2
Π ,
2
∆ states of the O
2+
/H
system. These have been obtained by means of a configu-
ration interaction molecular orbital method with several
hundred configurations [51.15]. It is clear from these
calculations that the only effective avoided crossings are
those involving the
4
Σ
−
and
4
Π at 3.7and4.8 a
0
,for
R (a. u.)
2
0.6
0.5
0.4
0.3
0.2
0.1
0
–0.1
–0.2
3456789101112
E (arb. units)
A
B
Fig. 51.1 Adiabatic potential energy curves of the
4
Σ
−
and
4
Π states of the OH
2+
molecular ion. The solid curves
designate
4
Π states, the dashed curves
4
Σ
−
states. The
dissociation limits A and B correspond respectively to [O
2+
(
3
P) + H(
2
S)] and [O
+
(
4
P) + H
+
]
Part D 51.1
Ion–Atom Charge Transfer Reactions at Low Energies 51.1 Molecular Structure Calculations 763
R (a. u.)
2
0.6
0.5
0.4
0.3
0.2
0.1
0
–0.1
–0.2
3456789101112
E (arb. units)
D
B
A
C
Fig. 51.2 Adiabatic potential energy curves of the
2
Σ
+
,
2
Π
and
2
∆ states of the OH
2+
molecular ion. The solid curves
designate
2
Σ
+
states, the dashed curves
2
Π states and the
dotted curve a
2
∆ state. The dissociation limits A, B, C and
D correspond respectively to [O
2+
(
1
S) + H(
2
S)], [O
2+
(
1
D) + H(
2
S)], [O
+
(
2
D) + H+]and[O
2+
(
3
P) + H(
2
S)]
which the energy separation is ≈ 0.1eV. The avoided
crossings involving the doublet states at 8.0, 8.5and
10 a
0
, for which the energy separation is ≈ 0.02 eV, are
diabatic. The avoided crossings for type II transitions oc-
cur at much shorter distances than for type I transitions.
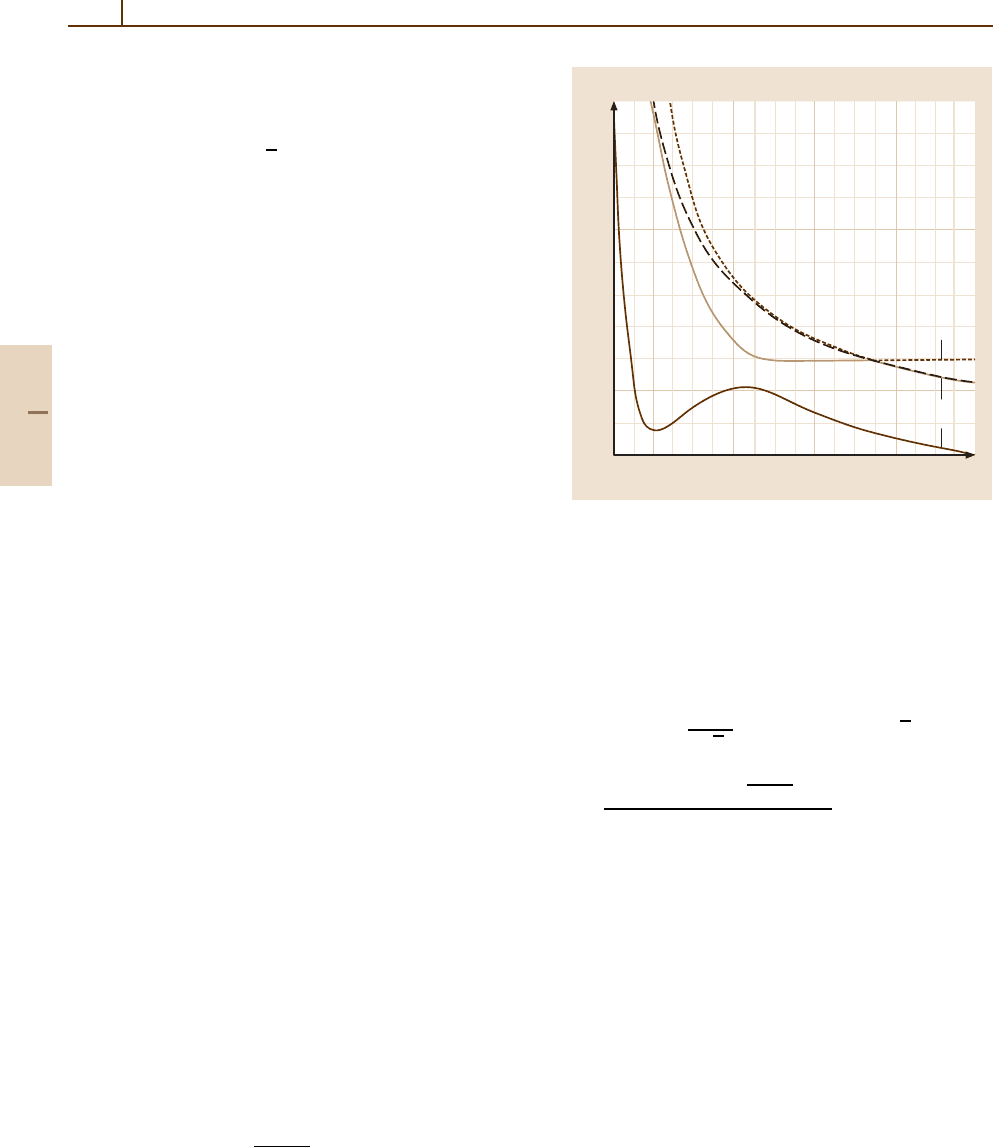
51.1.2 Model Potential Methods
Model potential methods offer an attractive alternative to
ab initio methods in treating type I reactions. To illustrate
the method [51.19, 20], we consider an effective one-
electron system composed of a spherically symmetric
ion X
q+
and a hydrogen atom. The model Hamiltonian
of the molecular ion XH
q+
is written as
H = T +V
X
(r
b
) −
1
r
a
+V
X
(R), (51.4)
where T is the electronic kinetic energy, r
a
and r
b
are
respectively the position vectors of the Rydberg electron
with respect to nuclei A and B, and V
X
(r) is the effective
potential of the ion core. The latter is usually expressed
in the parametric form
V
X
(r) =−
q +(Z −q)
1 +αr +βr
2
+γr
3
e
−δr
,
(51.5)
where Z is the ionic nuclear charge and the parameters
α,β,γ,δ,... are optimized to the spectroscopic data so
that the asymptotic energies of those Rydberg states of
X
(q−1)+
which govern the charge transfer process are
essentially exact.
The eigenvalues of H for a given internuclear
distance R are determined by standard variational tech-
niques, using a basis set of Slater-type orbitals in
prolate spheroidal coordinates [51.3]. As an example,
we present in Fig. 51.3 the potential energy curves of
the Al
3+
system which presents one Σ–Σ avoided
crossing around R
X
= 7.2 a
0
. Model potential methods
can also be used to treat multielectron systems such
as (XHe)
q+
. In long range collisions, the transition
probabilities are primarily determined by the asymp-
totic form of the electron wave functions far from the
nuclei. Thus even when multielectron targets are in-
volved, the effect of dynamic correlation can be small.
Since the asymptotic form of the wave functions may
be easily generated by model potential techniques, the
effect of static correlation can be taken into account
in a rather simple way. The method proposed here is
quite similar to that used by Grice and Herschbach
[51.21] to treat the long range configuration interac-
tion of ionic and covalent states in neutral atom–atom
collisions.
Internuclear distance
(
a
0
)
2
0.2
0
–0.2
–0.4
–0.6
46810
Adiabatic energies
(arb. units)
Al
+3
/H
Fig. 51.3 Adiabatic potential energies of AlH
3+
.Thefull
curve designates the
2
Σ state correlated to the [Al
3+
(3p)+
H (1s)] entry channel. The dotted and dashed curves des-
ignate respectively the
2
Σ and
2
Π states correlated to the
[Al
2+
(3p) + H
+
] electron capture channel
Part D 51.1
764 Part D Scattering Theory
For example, in the system X
q+
He, where as previ-
ously X
q+
is a closed shell ion, the energy separation at
a long range avoided crossing is given by [51.22]
∆ε(R
c
) ≡ 2
√
2
b
1σ
b
1s
a
nlλ
|V
X
+q/R|b , (51.6)
where the molecular orbitals a
nlλ
dissociating to
X
(q−1)+
nl
and b
1σ
(dissociating to a 1s orbital of He)
are generated from a model Hamiltonian of the form
H = T +V
X
(r
b
) −V
He
(r
a
) +V
X,He
(R), (51.7)
where V
He
is an effective potential describing the 1s
orbital of He. The orbital b
1s
is the 1s orbital of He
+
.
This expression is the optimal form of ∆ε(R
c
) which
can be achieved without the use of explicitly correlated
wave functions. Since both the a
nlλ
and b
1σ
orbitals
are generated from the same model Hamiltonian, the
calculation of the interaction matrix element in (51.6)is
simple. As an example, Fig. 51.4 presents the adiabatic
energies of the B
3+
/He system which has two avoided
Σ −Σ crossings, one at 4.6 a
0
, the other at 7.4 a
0
.
A similar extension to treat the case of capture by an
ion with one electron in a p shell can be made along the
same lines. See [51.23] for an application to the reaction
O
3+
(2p)
2
P +H → O
2+
(2p3p)
3
P +H
+
. (51.8)
A combination of model potential methods to rep-
resent the core electrons and ab initio molecular orbital
methods for the valence electrons has been successfully
developed [51.24] to treat some complex systems such
as C
3+
/H where both type I and II transitions take place.
The flexibility of the model potential parameters makes
it possible to choose them so that the energies of the
initial and final states are accurately reproduced.
51.1.3 Empirical Estimates
Electron capture cross sections at low energies are
largely controlled by two parameters: the crossing ra-
dius R
X
and the minimum energy separation ∆
X
.These
are the basic parameters required for the Landau–Zener
model, and it is useful to have a simple way of es-
timating them without having recourse to a complex
molecular structure calculation. Many empirical esti-
mates [51.25–27] have been proposed. However, it is
generally necessary to take into account the strong
-dependence of the electron capture channel states.
Defining α =
√
I
t
/13.6, where I
t
is the ionization po-
tential of the target (in eV), then Taulbjerg’s formula
Internuclear distance (a
0
)
2
–0.5
46 810
Adiabatic energies (arb. units)
–1
1s
2p
2s
Fig. 51.4 Adiabatic potential energies of BHe
3+
.Thedot-
ted curve designates the
1
Σ state correlated to the [B
3+
+
He(1s
2
)] entry channel. The short and long dashed curves
designate respectively the
1
Σ and
1
Π states correlated to
the [B
2+
(2p) + He
+
(1s)] electron capture channel. The
full curve designates the
1
Σ state correlated to the [B
2+
(2s) + He
+
(1s)] entry channel
is [51.27]
∆
X
(R
c
) =
18.26
√
q
f
nl
exp(−1.324αR
c
√
q ), (51.9)
where
f
nl
= (−1)
n+l−1
√
2l+1 Γ(n)
[Γ(n+l +1)Γ(n −l)]
1/2
. (51.10)
For type I systems, (51.9) is generally quite sat-
isfactory when the energy levels of the capture states
are well separated [51.28]. In that case, it can be used
to predict the main electron capture reaction windows
and obtain a reliable first estimate of the cross sec-
tions (in the energy range for which the Landau–Zener
model is valid). On the other hand, in cases where
there is a near degeneracy of the l states, serious er-
rors can occur [51.28] and the predictions are less
satisfactory.
For type II reactions, (51.9) must be modified by
a corrective factor to take account of the simultaneous
excitation of an electron from a 2s to 2p orbital. One
such modification, proposed by Butler and Dalgarno
[51.29], may give some useful idea of the main electron
capture processes, but its precision is uncertain.
Part D 51.1
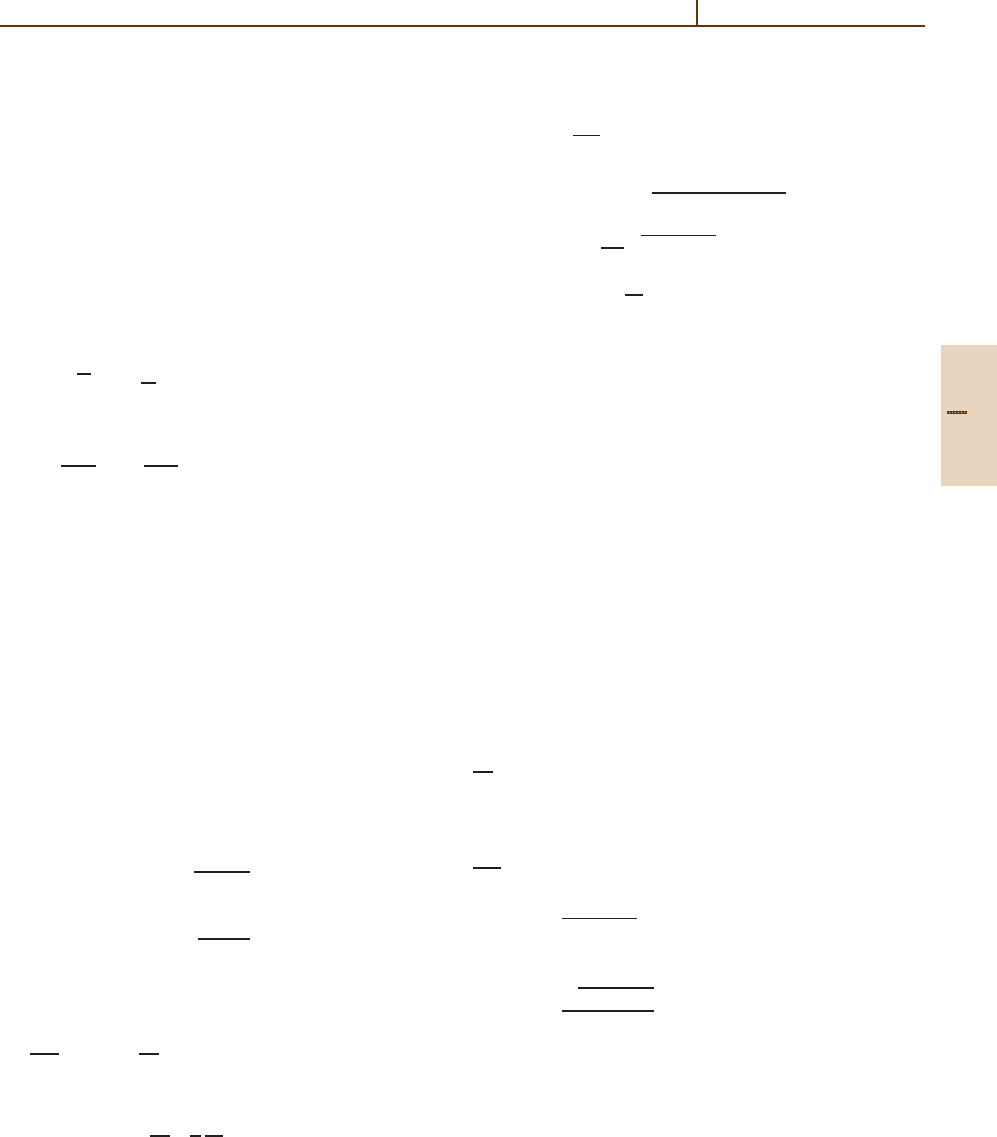
Ion–Atom Charge Transfer Reactions at Low Energies 51.2 Dynamics of the Collision 765
51.2 Dynamics of the Collision
The first step is to introduce a suitable set of scattering
coordinates which can automatically describe both the
excitation and rearrangement channels. The particular
choice of coordinate system is conditioned by practical
considerations. We have found Eckart coordinates to be
convenient [51.10]. Their application is straightforward
since it involves nonadiabatic matrix elements which can
be calculated by the conventional techniques of quan-
tum chemistry. The practical implementation of Eckart
coordinates leads to the introduction of an adiabatic
variable ξ defined as
ξ =
√
µ
R+
1
µ
s
,
where
s =
r · R
R
2
r −
r · R
2R
2
R
, (51.11)
µ is the reduced mass of the colliding system, r the
coordinate of the active electron with respect to the c.m.
of the colliding system and Rthe relative position vector
of the nuclei.
The adiabatic Eckart and Born–Oppenheimer equa-
tions differ only by terms of the order of 1/µ.Itmay
be assumed that the Eckart states are given to sufficient
accuracy by the Born–Oppenheimer adiabatic states des-
ignated by χ
i
(r; R). We expand the total wave function
of the system in the form
Ψ(r,ξ)=
χ
i
(r;ξ)F
i
(ξ) . (51.12)
(For a many-electron system, r represents the ensemble
of electron coordinates.) Decomposing F
i
(ξ) on a basis
set of symmetric top functions according to
F
i
(ξ) =
K,M
(−1)
K
2K +1
4π
1/2
× D
K
Λ,M
(θ, φ)
g
(k)
i
(ξ)
ξ
,
(51.13)
where {θ, φ}are the spherical polar coordinates of ξ,then
the radial functions g
(k)
i
(ξ) are solutions of the equation
d
2
dξ
2
g
(K)
+2A
d
dξ
g
(K)
+Wg
(K)
= 0 , (51.14)
where
A
mn
(ξ) =
χ
m
∂
∂ξ
+
z
ξ
∂
∂z
χ
n
δ(Λ
m
,Λ
n
),
(51.15)
B
mn
=
χ
m
∂
2
∂ξ
2
χ
n
,
(51.16)
W
mn
=
2µ(E −ε
n
) −
K(K +1) −Λ
2
n
R
2
δ
mn
+ B
mn
+
2
R
2
K(K +1) L
mn
, (51.17)
L
mn
=∓
χ
m
−2x
∂
∂z
χ
n
δ(Λ
m
,Λ
m
±1),
(51.18)
z, x are the components of r parallel to and perpendicular
to the direction of ξ in the classical collision plane,
respectively.
Since the ratio 1/µ is small, it is legitimate to replace
the matrix element χ
m
|∂/∂ξ|χ
n
by χ
m
|∂/∂R|χ
n
in
(51.15)and(51.16). Furthermore, all the matrix elem-
ents A
mn
and L
mn
vanish asymptotically to first order
in 1/µ. The modified radial and rotational matrix elem-
ents are identical to those obtained in the semiclassical
formalism with common translation factors.
The simplest way to solve (51.14) is to eliminate
the first-order derivative by transforming to a diabatic
representation in which the radial matrix elements van-
ish [51.30]
g
(K)
= Ch
(K)
, (51.19)
where
d
dξ
C + AC = 0 , C(∞) = I .
(51.20)
Equation (51.14) then reduces to
d
2
dξ
2
h
(K)
−2µV
d
h
(K)
+
2µE −
K(K +1)
ξ
2
h
(K)
= 0 (51.21)
with
V
d
= V
d
E
−
√
K(K +1)
µR
2
V
D
R
, (51.22)
V
d
E
= C
−1
εC , V
D
R
= C
−1
LC . (51.23)
The solution of (51.21) and the subsequent extraction
of the scattering matrix S may be carried out us-
ing an extension of the log derivative method [51.31],
adapted to the case of a repulsive Coulomb poten-
tial in one or more of the scattering channels [51.32].
Part D 51.2
766 Part D Scattering Theory
This method is particularly stable and advantageous
to use at low energies for problems of the type con-
sidered here. Of course, at energies exceeding a few
hundred eV, rapid oscillations of the radial function ren-
der the method rather time consuming. But the method
is usable up to keV energies. However, for higher
energies exceeding 1 keV, semiclassical methods are
preferable.
51.3 Radial and Rotational Coupling Matrix Elements
Two independent methods are employed for the de-
termination of radial coupling matrix elements A
mn
:
the first based on a direct numerical differentiation of
the expansion coefficients of the wave function, the
second on a variant of the Hellman–Feynman (HF)
theorem. In principle, the HF method is three times
faster than the direct numerical method, since the eigen-
vectors need to be calculated only at the value of R
concerned. However, the real gain in computing is not
always appreciable, the HF theorem being more sen-
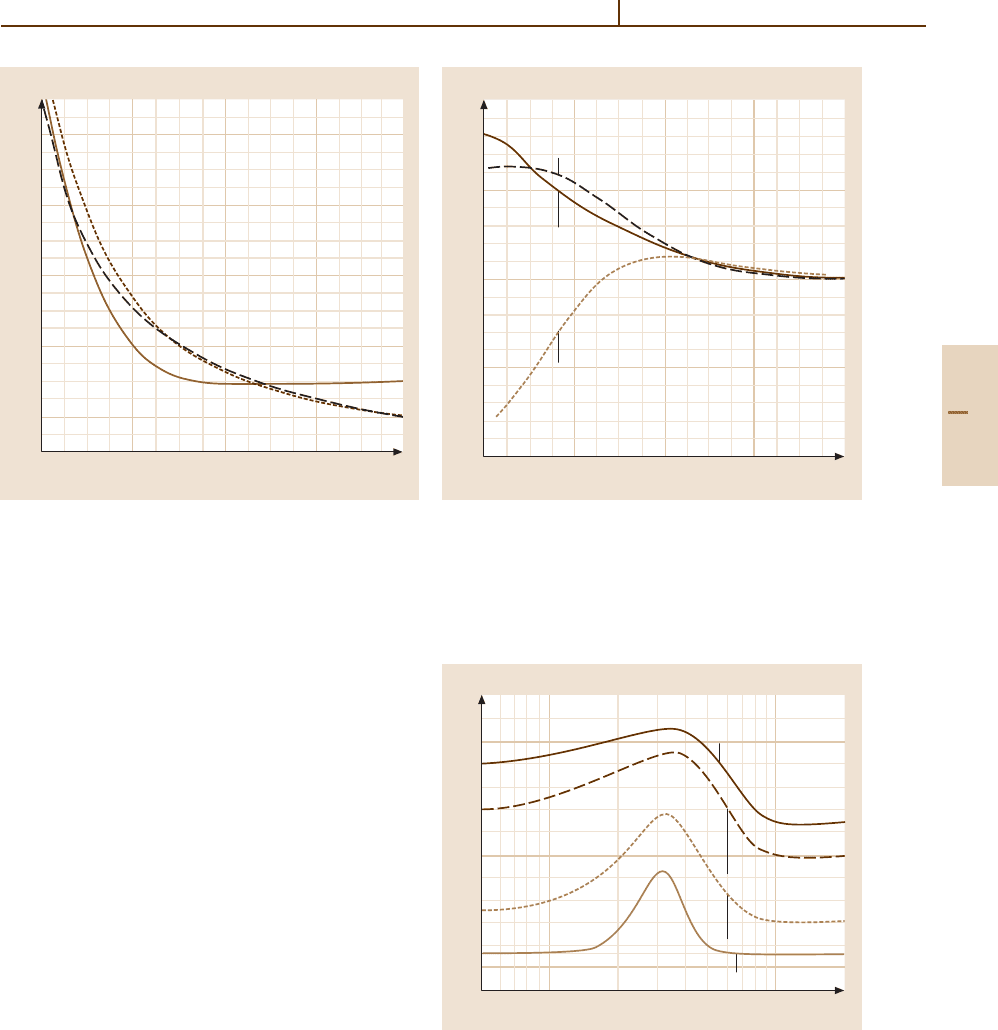
Radial couplings
0
–0.5
Internuclear distance (
a
0
)
24 1068
Origin = Al
+3
CTF
Al
+3
/H
Origin = H
Fig. 51.5 Radial coupling matrix elements between the two
2
Σ states of AlH
3+
.Thefull curve designates the ma-
trix element of the CTF (or Eckart) type. The short and
long dashed curves designate the radial derivative with the
origin of electron coordinates respectively on the Al and
H nuclei
Fig. 51.6 Rotational coupling matrix elements between
the
2
Σ and
2
Π states correlated to the electron capture
channel. The designation of the curves is the same as
for Fig. 51.5
sitive to errors in the wave function than the direct
method. To achieve comparable accuracy, a larger ba-
sis set would be required in the molecular calculations,
and this offsets much of the theoretical gain in com-
puting time. The rotational coupling matrix elements
L
mn
are calculated numerically for each internuclear
distance.
Typical results for the radial and rotational matrix
elements are presented in Figs. 51.5 and 51.6 for the
Al
3+
/H system, illustrating the influence of translation
effects. The origin dependence of the matrix element
(without inclusion of translation) is weak in the vicin-
ity of an avoided crossing. Away from the crossing,
the origin dependence can be considerable. The corre-
sponding diabatic energies and couplings are given in
Figs. 51.7 and 51.8. For internuclear distances on the in-
ward side of the crossing, the diabatic states correspond
to a mixing of adiabatic states: it is clear that the mathe-
matical definition (51.20) of the diabatic representation
does not correspond to the empirical definition of the
Landau–Zener model (Sect. 51.5).
Internuclear distance (a
0
)
–0.6
–0.8
–1
–1.2
Rotational couplings
24 1068
CTF
Origin = H
Al
+3
/H
Origin = Al
+3
Part D 51.3
Ion–Atom Charge Transfer Reactions at Low Energies 51.4 Total Electron Capture Cross Sections 767
Diabatic energies (arb. units)
0.2
0
–0.2
–0.4
–0.6
Internuclear distance (
a
0
)
24 1068
Al
+3
/H
Fig. 51.7 Diagonal elements of the diabatic matrix of
ALH
3+
0.2
0.1
0
–0.1
–0.2
Internuclear distance (
a
0
)
24 1068
Al
+3
/H
Origin = Al
+3
CTF
Origin = H
Diabatic couplings
Fig. 51.8 Off-diagonal diabatic matrix element between the
two
2
Σ states of AlH
3+
51.4 Total Electron Capture Cross Sections
Although the selection rules for electron capture at low
energies are primarily governed by the avoided cross-
ings between adiabatic states of the same symmetry,
the combined effects of radial and rotational coupling
can be quite complex. In general, rotational coupling
effects are weak when capture occurs via an S state,
but they can be strong for capture to P, D and higher
L states.
In the case of Al
3+
/H, where capture to the (3p)
2
P
state of Al
2+
takes place via a three-state network of
two Σ and one Π states, rotational coupling between the
Σ and Π states is strong in the vicinity of the avoided
crossing and enhances the capture cross section con-
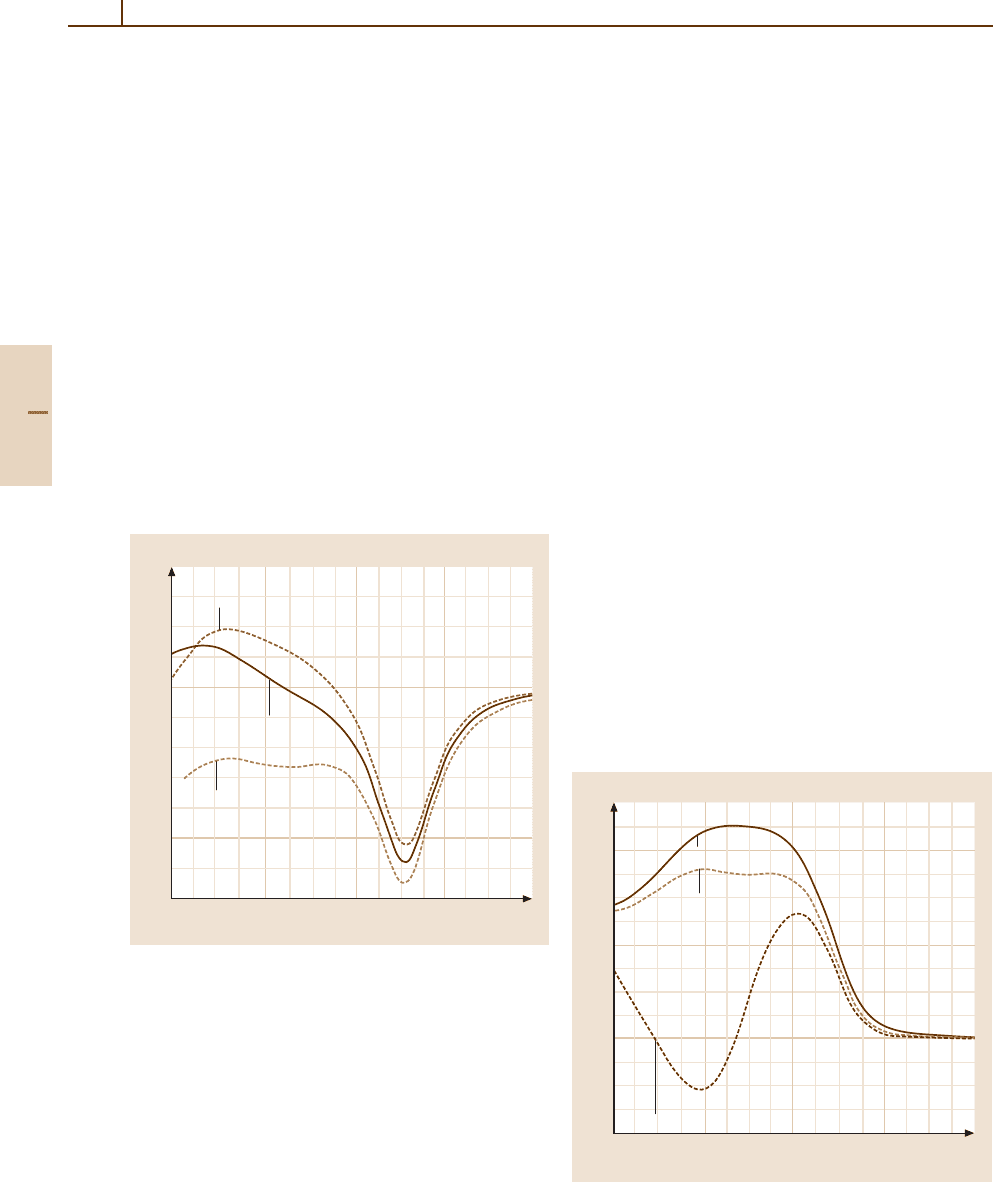
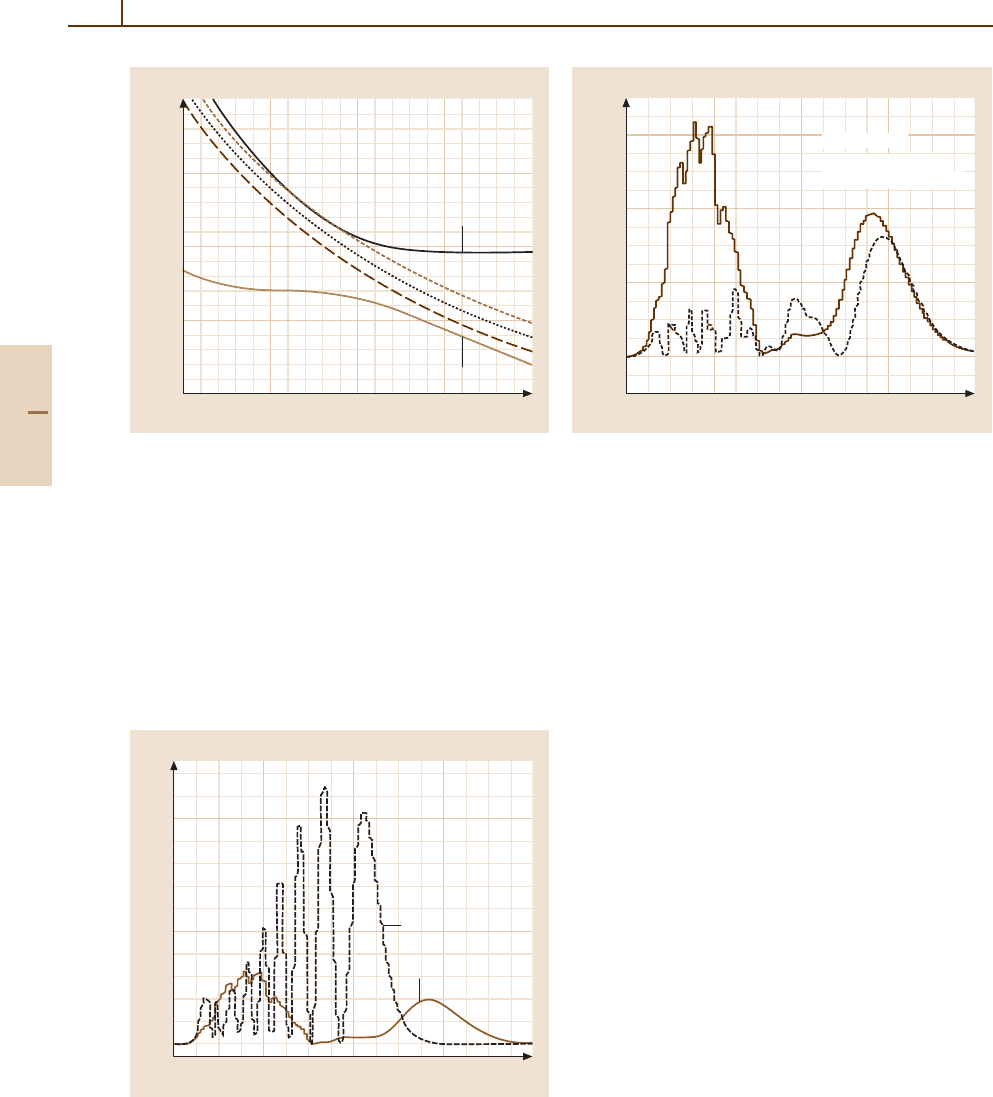
siderably. This phenomenon is illustrated in Fig. 51.9,
which shows the calculated total cross section at differ-
ent energies as a function of ∆, the energy separation of
the quasidegenerate diabatic
2
Σ and
2
Π exit channels at
the
2
Σ –
2
Σ crossing radius. The total cross section has
amaximumfor∆ = 0.08 eV. The cause can be easily
seen from the corresponding adiabatic potential ener-
gies (Fig. 51.10). For ∆ =0.8 eV, the potential energies
of the adiabatic
2
Σ entry channel and the
2
Π exit chan-
nel become tangential to one another, thereby inducing
a resonant effect.
100
50
0
Cross sections (a
2
)
10
–2
10
–1
Energy separation σ
3p
–π
3p
(σ
o
)
Al
+3
/H
E = 141.2 eV/amu
E = 84.7 eV/amu
E = 28.2 eV/amu
E = 8.5 eV/amu
Fig. 51.9 Results of three state (two
2
Σ and one
2
Π ) cal-
culations for electron capture in the Al
3+
/H system. The
cross sections are plotted as a function of the parameter ∆
(see text). The extreme sensitivity to ∆ illustrates the ne-
cessity of knowing the
2
Σ –
2
Π energy separation to high
accuracy. The numerical values on the curves designate the
collision energies in units of eV/amu
Part D 51.4
768 Part D Scattering Theory
–0.4
–0.45
–0.5
–0.55
–0.6
56789
Internuclear distance (a
0
)
Al
+3
/H adiabatic energies (arb. units)
σ1s
H
σ3p
Al
Fig. 51.10 Schematic diagram of the nondiagonal matrix
elements of AlH
3+
in the vicinity of the curve cross-
ing. The three broken curves correspond to different
2
Π
state potentials shifted from their calculated value by small
amounts
In the case of the B
3+
/He system, four molecu-
lar states are implicated in the collision process: three
Σ states (Σ
1
correlated to the
2
S exit channel, Σ
2
cor-
related to the
2
P exit channel and Σ
3
correlated to the
entry channel) and one Π state (correlated to the
2
P
exit channel). In order to understand better the rota-
0.02
0.01
0
02468
Cross section (a
0
2
)
Impact parameter (a
0
)
B
+3
/He
E
lab
= 6 keV
2s
2p
Fig. 51.11 Transition amplitudes for
2
Sand
2
P electron cap-
ture as a function of impact parameter in B
3+
/He collisions.
The solid curve refers to the
2
P contribution, the dotted
curve to the
2
S contribution
02468
0.006
0.004
0.002
0
Cross section (a
0
2
)
Impact parameter (a
0
)
B
+3
/He
E
lab
= 6 keV
with rot. coupling
without rot. coupling
Fig. 51.12 Influence of rotational coupling on the
2
P elec-
tron capture cross section in B
3+
/He collisions. The
solid curve refers to the complete calculation, the dot-
ted curve to the calculation with only radial coupling
included
tional coupling mechanism, Figs. 51.11 and 51.12 show
the
2
Sand
2
P electron capture transition amplitudes as
a function of angular momentum (impact parameter)
for an energy of 6 keV, where rotational coupling is
of major importance [51.14, 33]. The
2
P electron cap-
ture transition amplitude exhibits 2 maxima, one for
an impact parameter of 1.6 a
0
, the other for an impact
parameterof5.7 a
0
, corresponding respectively to cap-
ture via Σ
2
–Π crossing around R = 2 a
0
and the outer
Σ
2
–Σ
3
crossing around R = 7.4 a
0
. It is clear from
Fig. 51.12 that at very short internuclear distances, ro-
tational coupling is much more important than radial
coupling. At the outer crossing (which is nearly dia-
batic), radial coupling is dominant. This result may be
generalized. When the avoided crossing has a largely
diabatic character, as for 3p capture in Si
2+
/H [51.34]
or 3d capture in C
4+
/H [51.10], the inclusion of rota-
tional coupling is fairly weak, affecting principally the
population of the sub-m levels and less appreciably the
total capture cross section into a given l state. In this
case, translation effects are of more importance than
rotational coupling.
In the case of O
2+
/H (a particularly important sys-
tem in astrophysical plasmas), the existence of several
adiabatic states correlated to the entry channel leads to
many interesting features, typical of open p shell ions.
The favored reaction channel via the
4
Σ
−
and
4
Π states
involves simultaneous electron capture into a 2p orbital
Part D 51.4
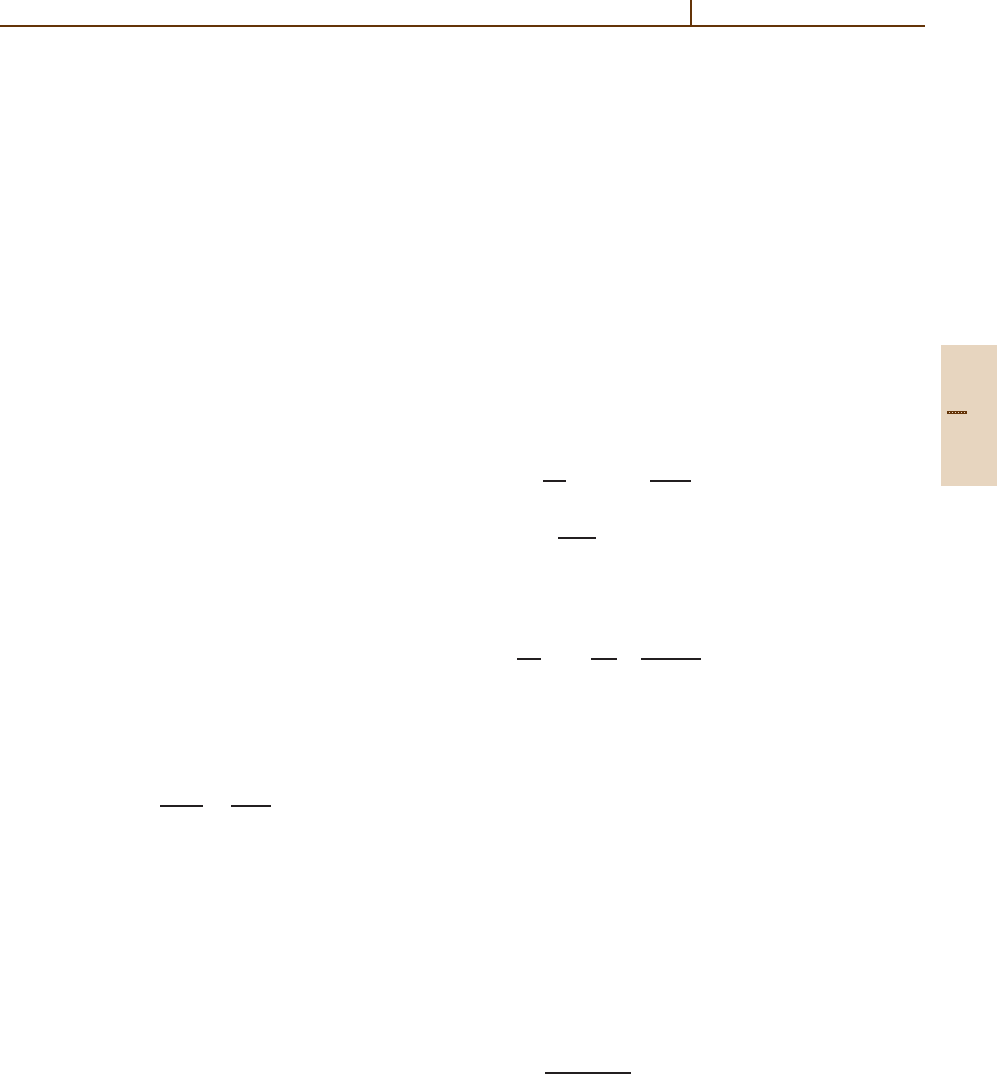
Ion–Atom Charge Transfer Reactions at Low Energies 51.6 Differential Cross Sections 769
and excitation of a 2s orbital. The avoided crossing is due
to electron correlation. Rotational mixing of the
4
Σ
−
and
4
Π states leads to a large enhancement of the cross
section at energies exceeding a few tens of eV [51.16].
On the other hand, the avoided crossings involving the
2
Σ
+
and
2
Π states around 8 a
0
are too diabatic to con-
tribute to an electronic transition. As a consequence, the
metastable
1
D ions can only react via a curve crossing
at small distances (2.5 a
0
). The cross section is much
smaller than for ground
3
P state capture.
51.5 Landau–Zener Approximation
If a rapid estimation of the cross sections is all that
is needed, the Landau–Zener method can be used with
advantage, provided that the molecular structure par-
ameters are known accurately. This method, based on
an approximate solution of the dynamical equations in
a semiclassical formalism (Chapt. 49), is satisfactory
for the dominant channels. Aside from the transi-
tion being assumed to be localized at the crossing
point, the method can easily take account of trajec-
tory effects at low energies. On the other hand, it is
unreliable for the weaker channels and it makes al-
lowance neither for translation effects nor for rotational
coupling.
The cross section for capture into a state n via a curve
crossing located at R
X
is given by
Q
LZ
n
= 2π
ρ
max
0
2p(1 − p)ρ dρ, (51.24)
where p, the probability for a single passage trajec-
tory (impact parameter) through the crossing, is given
by
p = exp
−2π
∆E
nl
2
2
1
v∆F
,
(51.25)
∆F being the difference in slope of the covalent and
ionic diabatic curves at R
X
, ∆
X
the energy separation
of the diabatic curves at R
X
and v the radial vel-
ocity at R
X
. It should be recalled that there is no very
rigorous definition of the diabatic curves (which are re-
quired to obtain DF).For long distance crossings, the
simplest (and probably the most satisfactory) estimate
is that based on the asymptotic forms of the diabatic
states
∆F =
∂
∂R
V
1
(R) −
q −1
R
R=R
X
,
V
1
(R) =−
q
2
α
d
2R
4
, (51.26)
where α
d
is the polarizability of the target. The radial
velocity is given by
v =
2E
µ
1 −
ρ
2
R
2
X
−
V
1
(R
X
)
E
1/2
. (51.27)
The inclusion of the attractive polarization poten-
tial V
1
considerably increases the cross section at low
energies, since trajectories with impact parameters much
greater than R
X
contribute to the cross section. This
effect can introduce a negative energy dependence of
the cross section in the limit of low energies, of the
same kind as the Langevin model for ion–molecule
reactions.
51.6 Differential Cross Sections
Differential cross sections at large scattering angles (cor-
responding to small impact parameters) enable one to
probe details of the collision dynamics not readily ob-
tainable from total cross sections, which tend to be
dominated by the contribution from small angle scat-
tering (large impact parameters).
Their determination is staightforward once the S ma-
trix elements have been extracted from the asymptotic
solution of the coupled equations (51.21). The scattering
amplitude f
fi
(ϑ) for scattering through the c.m. angle ϑ
is given by
f
fi
(ϑ) =
1
2i(k
i
k
f
)
1/2
∞
l=0
(2l+1)
S
l
fi
−δ
fi
× P
l
(cos ϑ) exp[iα
f
(l)] , (51.28)
where k
i
and k
f
are the wave numbers of the initial
and final channels, S
l
fi
the S-matrix element for the i to
Part D 51.6
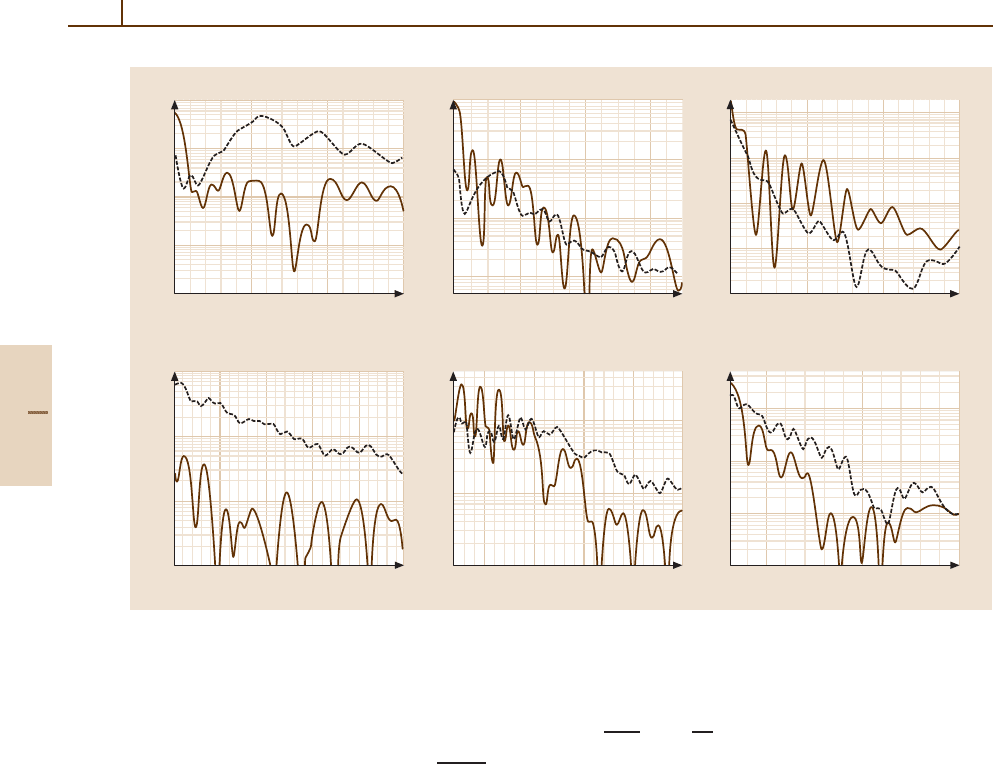
770 Part D Scattering Theory
10
2
10
1
1
10
–1
10
–2
0 0.5 1 1.5
10
4
10
3
10
2
10
1
0 0.2 0.4
10
5
10
4
10
3
10
2
10
1
0 0.1 0.2 0.3
10
1
1
10
–1
10
–2
1.5 2 3 42.5 3.5
10
1
1
10
–1
1 1.5 2 2.5 3
10
2
10
1
1
10
–1
0.5 1 1.5
0.6
Differential cross sections (10
–16
cm
2
/sr)
Angle (deg)
E
lab
= 0.3 keV
Differential cross sections (10
–16
cm
2
/sr)
Angle (deg)
E
lab
= 1.8 keV
Differential cross sections (10
–16
cm
2
/sr)
Angle (deg)
E
lab
= 6 keV
Differential cross sections (10
–16
cm
2
/sr)
Angle (deg)
E
lab
= 0.3 keV
Differential cross sections (10
–16
cm
2
/sr)
Angle (deg)
E
lab
= 1.8 keV
Differential cross sections (10
–16
cm
2
/sr)
Angle (deg)
E
lab
= 6 keV
Fig. 51.13 Differential cross sections (10
−16
cm
2
/sr) for electron capture in B
3+
/He collisions as a function of scattering
angle for ion energies of 0.3, 1.8and6keV.Thesolid curves refer to
2
S capture, the dotted curves to
2
P capture
f transition, and α
f
(l) the partial wave Coulomb phase
shift for the final channel:
α
f
(l) = arg Γ(l+1 +iγ
f
), γ
f
=
µq
1
q
2
k
f
.
(51.29)
The charges of the two collision partners in the final
state are designated q
1
and q
2
,andµ is the nuclear
reduced mass. The differential cross section is evaluated
as
dσ
fi
dΩ
(ϑ) =
k
f
k
i
| f
fi
(ϑ)|
2
. (51.30)
Figure 51.13 shows some typical differential cross
sections for capture to the (2s)
2
Sand(2p)
2
P states of
B
2+
in the B
3+
/He system. The oscillations observed
in the differential cross sections are of Stückelberg type.
A knowledge of differential cross sections is essential for
estimating acceptance angles in laboratory experiments.
51.7 Orientation Effects
Recent experiments on the B
3+
/He system [51.35, 36]
show that there is a strong tendency for electron capture
to produce strongly oriented states at small scatter-
ing angles. This propensity for orientation is a direct
measure of rotational coupling between the Σ and
Π molecular states converging to the
2
P asymptotic
state [51.37].
The orientation and alignment parameters, which
characterize the polarization of the emitted photons,
can be simply expressed in terms of the scattering
amplitudes for electron capture to the magnetic sub-
levels. These scattering amplitudes can be directly
obtained from the scattering matrix. However, care
must be exercised in the definition of the scattering
amplitudes. In most applications where an adiabatic
representation of the collision dynamics is used, the
quantization axis is taken to be in the direction of
the internuclear axis. For most polarization measure-
Part D 51.7
Ion–Atom Charge Transfer Reactions at Low Energies 51.7 Orientation Effects 771
ments, it is more convenient to define the quantization
axis with respect to an axis perpendicular to the col-
lison plane. But it is straightforward to express the
orientation and alignment parameters in terms of the
scattering amplitudes obtained with respect to the mo-
lecular frame.
In accordance with customary conventions, in
Fig. 51.14, the scattering plane contains the X and
Z axes. The Y axis, perpendicular to the scattering
plane, is taken to be the quantization axis. Let XYZ
be the laboratory frame and xyz the body-fixed frame
defined as above. The scattering amplitudes calculated
in Sect. 51.3 are expressed with respect to the body-fixed
frame xyz. The scattering amplitudes f
M
Y
=±1
in the lab-
oratory frame are related to the amplitudes f
Σ
Z
, f
Π
+
Z
in
the body-fixed frame by
f
M
Y
=±1
=
1
√
2
f
Σ
Z
∓ f
Π
+
Z
.
(51.31)
The right-hand and left-hand circular polarizations
(RHC and LHC respectively) are then defined as
RHC =|f
M
Y
=−1
|
2
=
1
2
f
Σ
Z
2
+
f
Π
+
Z
2
+Im
f
Σ
Z
f
∗
Π
+
Z
,
(51.32)
LHC =|f
M
Y
=+1
|
2
=
1
2
f
Σ
Z
2
+
f
Π
+
Z
2
−Im
f
Σ
Z
f
∗
Π
+
Z
,
(51.33)
and the circular polarization as
L =
RHC −LHC
RHC +LHC
=
2Im
f
Σ
Z
f
∗
Π
+
Z
f
Σ
Z
2
+
f
Π
+
Z
2
. (51.34)
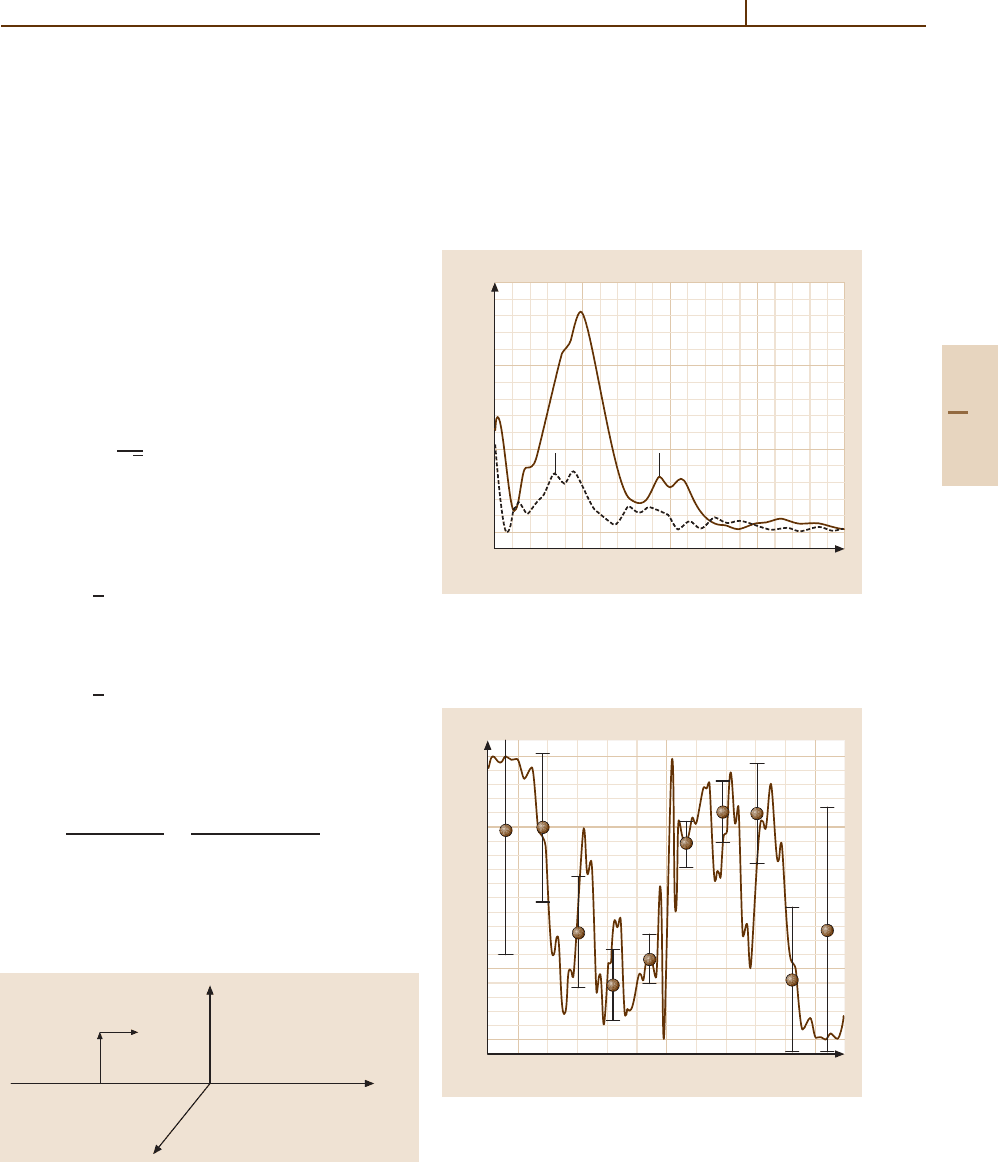
Figures 51.15 and 51.16 show the RHC, LHC and
L quantities for an incident ion energy of 1.5keV,
where comparison with experiments [51.35, 36] can
v
b
X, z
Z, y
Y, x
Fig. 51.14 coordinate systems for scattering
be made. The strong propensity for orientation of the
2
P state is clearly exhibited for small scattering angle
(ϑ<0.2
◦
). At larger angles (smaller impact parameters),
the propensity decreases and even reverses (ϑ>0.4
◦
).
We have also plotted on Fig. 51.16 the experimental data
of Roncin et al. [51.35]. The agreement with experiment
is very satisfactory.
1.5
×10
4
10
4
5000
0
0 0.1 0.2 0.3 0.4
Angle (deg)
RHC LHC (arb. units)
B
+3
/He
E
lab
= 1.5 keV
LHC RHC
Fig. 51.15 Right-hand circular polarization (full curve)and
left-hand circular polarization (dashed curve)for
2
P elec-
tron capture in B
3+
/He collisions as a function of scattering
angle for E = 1.5keV
1
0.5
0
–0.5
–1
–0.5 0 0.5
Angle (deg)
Circular polarization
Fig. 51.16 Circular polarization for
2
P electron capture in
B
3+
/He collisions as a function of scattering angle for
E = 1.5keV. The solid circles (with the error bars) are
taken from [51.35]
Part D 51.7
