Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics
Подождите немного. Документ загружается.


742 Part D Scattering Theory
izes the extent of the interaction region. For instance, for
the exchange interaction between two atoms, L
0
cor-
responds to the distance of closest approach of the
colliding particles, while a is the range of the exponen-
tial decrease of the interaction. Typically, L
0
noticeably
exceeds a .
49.1.2 Adiabatic
and Diabatic Electronic States
Let r refer to a set of electronic coordinates in
a body-fixed frame related to the nuclear framework
of a colliding system, and let R refer to a set of
nuclear coordinates determining the relative position
of nuclei in this system. A configuration of electrons
and nuclei in a frame fixed in space is completely
determined by r, R, and the set of Euler angles Ω,
which relate the body-fixed frame to the space-fixed
frame. If the total Hamiltonian of the system is
H (r, R,Ω), the stationary state wave function satisfies
the equation
H (r, R,Ω)Ψ
E
(r, R,Ω)= EΨ
E
(r, R,Ω). (49.3)
The electronic adiabatic Hamiltonian H(r;R) is defined
to be the part of H(r, R,Ω)in which the kinetic energy
of the nuclei is ignored. The adiabatic electronic func-
tions ψ
n
(r;R) are defined as eigenfunctions of H(r;R)
at a fixed nuclear configuration R:
H(r;R)ψ
n
(r;R) =U
n
(R)ψ
n
(r;R). (49.4)
The eigenvalues U
n
(R) are called adiabatic potential
energy surfaces (adiabatic PES). In the case of a diatom,
the set R collapses into a single coordinate, the internu-
clear distance R,andthePES become potential energy
curves, U
n
(R). The functions ψ
n
(r;R) depend expli-
citly on R and implicitly on the Euler angles Ω.The
significance of the adiabatic PES is related to the fact
that in the limit of very low velocities, a system of nuclei
will move across a single PES. In this approximation,
called the adiabatic approximation, the function U
n
(R)
plays the part of the potential energy which drives the
motion of the nuclei.
An electronic diabatic Hamiltonian is defined for-
mally as a part of H,i.e.,H
0
= H +∆H.The
partitioning of H into H
0
and ∆ H is dictated by the
requirement that the eigenfunctions of H
0
, called dia-
batic electronic functions φ
n
, depend weakly on the
configuration R. The physical meaning of this weak de-
pendence is different for different problems. A perfect
diabatic basis set φ
n
(r) is R-independent; for practical
purposes one can use a diabatic set which is consid-
ered as R-independent within a certain region of the
configuration space R.
Two basis sets ψ
n
and φ
n
generate the matrices
φ
m
|H|φ
n
=H
mn
,
φ
m
|H |φ
n
=H
mn
+ D
mn
,
ψ
m
|H |ψ
n
=U
n
(R)δ
mn
+D
mn
. (49.5)
The eigenvalues of the matrix H
mn
are U
n
. D
mn
is the
matrix of dynamic coupling in the diabatic basis, and
D
mn
is the matrix of dynamic coupling in the adiabatic
basis; the former matrix vanishes for a perfect diabatic
basis. All the above matrices are, in principle, of infi-
nite order. For low-energy collisions, the use of finite
matrices of moderate dimension, will usually suffice.
Diabatic PES are defined as the diagonal elem-
ents H
nn
. The significance of the diabatic PES is that for
velocities which are high [but still satisfy (49.1)] the sys-
tem moves preferentially across diabatic PES, provided
that the additional conditions discussed in Sect. 49.3 are
fulfilled.
For a given finite adiabatic basis ψ
n
(r;R ), a perfect
diabatic basis φ
n
(r) can be constructed by diagonalizing
the matrix D
nm
(R). The two basis sets are related by
a unitary transformation
ψ
n
(
r;R
)
=
n
C
nn
(
R
)
φ
n
(r). (49.6)
49.1.3 Nonadiabatic Transitions:
The Massey Parameter
Deviations from the adiabatic approximation manifest
themselves in transitions between different PES which
are induced by the dynamic coupling matrix D.Atlow
energies, the transitions usually occur in localized re-
gions of nonadiabatic coupling (NAR). In these regions,
the motion of nuclei in different electronic states is
coupled, and in general it cannot be interpreted as being
driven by a single potential.
An important simplifying feature of slow adiabatic
collisions is that typically the distance between differ-
ent NAR is substantially larger than the extents of each
NAR. This makes it possible to formulate simple models
for the coupling in isolated NAR, and subsequently to
incorporate the solution for nonadiabatic coupling into
the overall dynamics of the system.
For a system of s nuclear degrees of freedom, there
are the following possibilities for the behavior of PES
within NAR:
Part D 49.1
Adiabatic and Diabatic Collision Processes at Low Energies 49.2 Two-State Approximation 743
(i) If two s-dimensional PES correspond to electronic
states of different symmetry, they can cross along an
(s−1)-dimensional line. For a system of two atoms,
s = 1, and so two potential curves of different symmetry
can cross at a point.
(ii) If two s-dimensional PES correspond to electronic
states of the same symmetry, they can cross along an
(s−2)-dimensional line. For a system of two atoms,
s = 1, and so two potential curves of different symmetry
cannot cross. If they have a tendency to cross, they will
exhibit a pattern which is called an avoided crossing or
a pseudocrossing.
(iii) If two s-dimensional PES correspond to electronic
states of the same symmetry in the presence of spin–orbit
coupling, they can cross along an (s−3)-dimensional
line.
Statement (ii) applied to a two-atom system is known
as the Wigner–Witmer noncrossing rule.
The efficiency of the nonadiabatic coupling between
two adiabatic electronic states is determined, according
to the adiabatic principle of mechanics (both classical
and quantum), by the value of the Massey parameter ζ,
which represents the product of the electronic transition
frequency ω
el
and the time τ
nuc
that characterizes the rate
of change of electronic function due to nuclear motion.
Putting ω
el
≈ ∆U(R)/ ,(∆U is the spacing between
any two adiabatic PES), and τ
nuc
= ∆L/v(R),(∆L is
a certain range which depends on the type of coupling),
we get
ζ(R) = ω
el
τ
nuc
= ∆U(R)∆L/ v(R). (49.7)
The nonadiabatic coupling is inefficient at those con-
figurations R where ζ(R) 1. If ζ(R) is less than or of
the order of unity, the nonadiabatic coupling is efficient,
and a change in adiabatic dynamics of nuclear motion is
very substantial.
The following relations usually hold for the param-
eters ∆L, a, L
0
for slow collisions:
∆L a L
0
. (49.8)
When the nonadiabatic coupling is taken into
account, the total (electronic and nuclear) wave func-
tion Ψ
E
can be represented as a series expansion in
ψ
n
or φ
n
(the Euler angles Ω are suppressed for brevity):
Ψ
E
(r, R) =
n
ψ
n
(r;R )χ
nE
(R)
=
n
φ
n
(r)κ
nE
(R). (49.9)
Here χ
nE
(R) and κ
nE
(R) are the functions which
have to be found as solutions to the coupled equa-
tions formulated in the adiabatic or diabatic electronic
basis, repectively [49.1, 2]. In general, different contri-
butions to the first sum in (49.9) can be associated with
nonadiabatic transition probabilities between different
electronic states.
A practical means of calculating functions χ
nE
(R)
[or κ
nE
(R)] consists of expanding them over certain
basis functions Ξ
nν
(R
),whereR
denotes all coordi-
nates R except for the interparticle distance R. Writing
χ
nE
(R) =
ν
Ξ
nν
(R
)ξ
nνE
(R), (49.10)
one arrives at a set of coupled second-order equations
for the unknown functions ξ
nνE
(R) (the scattering equa-
tions) [49.1]. In the semiclassical approximation, these
equations become a set of first-order equations for the
amplitudes of the WKB counterparts of ξ
nνE
(R).Atthe
next step of simplification, in the common trajectory ap-
proximation, the variable R is changed into the time
variable t, the latter being related to R via the classical
trajectory R = R(t) [49.2]. In the adiabatic approxima-
tion, the total wave function is represented by a single
term in the first sum of (49.9):
Ψ
E
(r, R) = ψ
n
(r;R)χ
nE
(R). (49.11)
49.2 Two-State Approximation
49.2.1 Relation Between Adiabatic
and Diabatic Basis Functions
In the two-state approximation, the basis of electronic
functions consists of two states. In this case, the elements
of the matrix C in (49.6) are expressed through a single
parameter only, a mixing or rotation angle θ:
ψ
1
(r;R) = cos θ(R)φ
1
(r) +sin θ(R)φ
2
(r),
ψ
2
(r;R) =−sin θ(R)φ
1
(r) +cos θ(R)φ
2
(r).
(49.12)
The rotation angle, θ(R), is expressed via the diag-
onal and off-diagonal matrix elements of the adiabatic
Hamiltonian H in the diabatic basis φ
1
,φ
2
:
tan 2θ(R) =
2H
12
(R)
H
11
(R) − H
22
(R)
.
(49.13)
Part D 49.2

744 Part D Scattering Theory
The eigenvalues of H in terms of H
ik
are
U
1,2
(R) =
[
H
11
(R) + H
22
(R)
]
/2 ±∆U(R)/2 ,
(49.14)
where
∆U(R) =
[
H
11
(R) − H
22
(R)
]
2
+4H
2
12
(R)
1/2
.
(49.15)
The matrix elements H
ik
are expressed via the adia-
batic potentials and the rotation angle by
H
11
(R) + H
22
(R) = U
1
(R) +U
2
(R),
H
11
(R) − H
22
(R) = ∆U(R) cos 2θ(R),
H
12
(R) = (1/2)∆U(R) sin 2θ(R).
(49.16)
49.2.2 Coupled Equations
and Transition Probabilities
in the Common Trajectory
Approximation
A two-state nonadiabatic wave function Ψ(r , R) can be
written as an expansion into either adiabatic or diabatic
electronic wave functions:
Ψ(r;R) = ψ
1
(r;R)α
1
(R) +ψ
2
(r;R)α
2
(R),
Ψ(r;R) = φ
1
(r)β
1
(R) +φ
2
(r)β
2
(R), (49.17)
in which the nuclear wave functions satisfy two coupled
s-dimensional Schrödinger equations [49.1].
In the common trajectory approximation, the motion
of the nuclei is described by the classical trajectory, i. e.,
by a one-dimensional manifold Q(t) embedded in the
s-dimensional manifold R. A section of PES along this
one-dimensional manifold determines a set of effective
potential energy curves (PEC). In the case of atomic
collisions, Q coincides with the interatomic distance R,
and the effective PEC are just ordinary PEC.
A common trajectory counterpart of (49.17)is
Ψ(r, t) = ψ
1
[
r;Q(t)
]
a
1
(t) +ψ
2
[
r;Q(t)
]
a
2
(t),
Ψ(r;t) = φ
1
(r)b
1
(t) +φ
2
(r)b
2
(t). (49.18)
The adiabatic expansion coefficients a
k
(t) satisfy the set
of equations
i
da
1
dt
=U
1
(Q)a
1
+i
˙
Qg(Q)a
2
,
i
da
2
dt
=−i
˙
Qg(Q)a
1
+U
2
(Q)a
2
, (49.19)
where g(Q) =ψ
1
|∂/∂Q|ψ
2
=dθ/ dQ,andQ =Q(t).
The diabatic expansion coefficients b
k
(t) satisfy the set
of equations
i
db
1
dt
= H
11
(Q)b
1
+ H
12
(Q)b
2
,
i
db
2
dt
= H
21
(Q)b
1
+ H
22
(Q)b
2
. (49.20)
Clearly, for a system of two atoms, Q ≡ R.
Solutions to (49.19)and(49.20) are equivalent, pro-
vided that the initial conditions are matched, and the
transition probability is properly defined.
For a given trajectory, it is customary to identify
the center of the NAR with a value of Q = Q
p
which
corresponds to the real part of the complex-valued co-
ordinate Q
c
at which two adiabatic PES cross. The
crossing conditions in the adiabatic and diabatic rep-
resentations are
U
1
(Q
c
) −U
2
(Q
c
) = 0 , (49.21)
or
H
11
(Q
c
) − H
22
(Q
c
)
2
+4H
2
12
(Q
c
) = 0 . (49.22)
Since Q represents a one-dimensional manifold, the
crossing condition (49.22) is satisfied for a complex
value of Q =Q
s
unless H
12
=0. Then, by definition, the
location of the NAR centeris identified with Q
p
through
Q
p
= Re(Q
c
), (49.23)
where Q
c
is that value of Q
s
which possesses the
smallest imaginary part, and Re denotes the real part.
For the case when the regions of nonadiabatic coup-
ling are well localized, the function g(Q) possesses
a pronounced maximum at (or close to) Q
p
, the width
∆Q
p
of which determines the range of the NAR; nor-
mally ∆Q
p
is about Im (Q
c
), with Im denoting the
imaginary part. The two Eqs. (49.19) decouple on both
sides of this maximum. A solution of the equations for
the nonadiabatic coupling across an isolated maximum
of g(Q) yields the so-called single-passage (or one-way)
transition amplitude and transition probability. For this
problem, the time t = 0 can be assigned to the maxi-
mum point of g[Q(t)]. Assuming that away from t = 0
the decoupling occurs rapidly enough, the nonadiabatic
transition probability
P
12
=|a
2
(∞)|
2
, (49.24)
provided that a solution to (49.19) corresponds to the
initial conditions,
a
1
(−∞) = 1 , a
2
(−∞) = 0 . (49.25)
Part D 49.2

Adiabatic and Diabatic Collision Processes at Low Energies 49.2 Two-State Approximation 745
In the limit of almost adiabatic conditions where P
12
is
very small, the following equation holds [49.3]:
P
12
= exp
−
2
Im
t
c
t
r
U
1
[Q(t)]−U
2
[Q(t)]
dt
,
(49.26)
where t
c
is a root of
Q(t
c
) = Q
c
. (49.27)
Here t
r
is any real-valued time. Equation (49.26) is valid
when the exponent is large, so that P
12
is exponentially
small.
The property of the function g(Q) to pass through
a single narrow maximum ensures that the rotation angle
away from the maximum tends to constant values, and
adiabatic functions in these regions are expressed by
certain linear combinations of diabatic functions with
constant mixing coefficients. These linear combinations
should serve as the initial condition on one side of the
coupling region, and as the proper final state on the
other, when the problem of a nonadiabatic transition
between adiabatic states is treated in the diabatic rep-
resentation. The same property of the function g(Q)
implies that a common trajectory needs to be defined
only locally, within a given NAR, and not globally, in
the full configuration space.
49.2.3 Selection Rules
for Nonadiabatic Coupling
In the general case, the coupling between adiabatic states
or diabatic states is controlled by certain selection rules.
The most detailed selection rules exist for a system of
two colliding atoms, since this system possesses a high
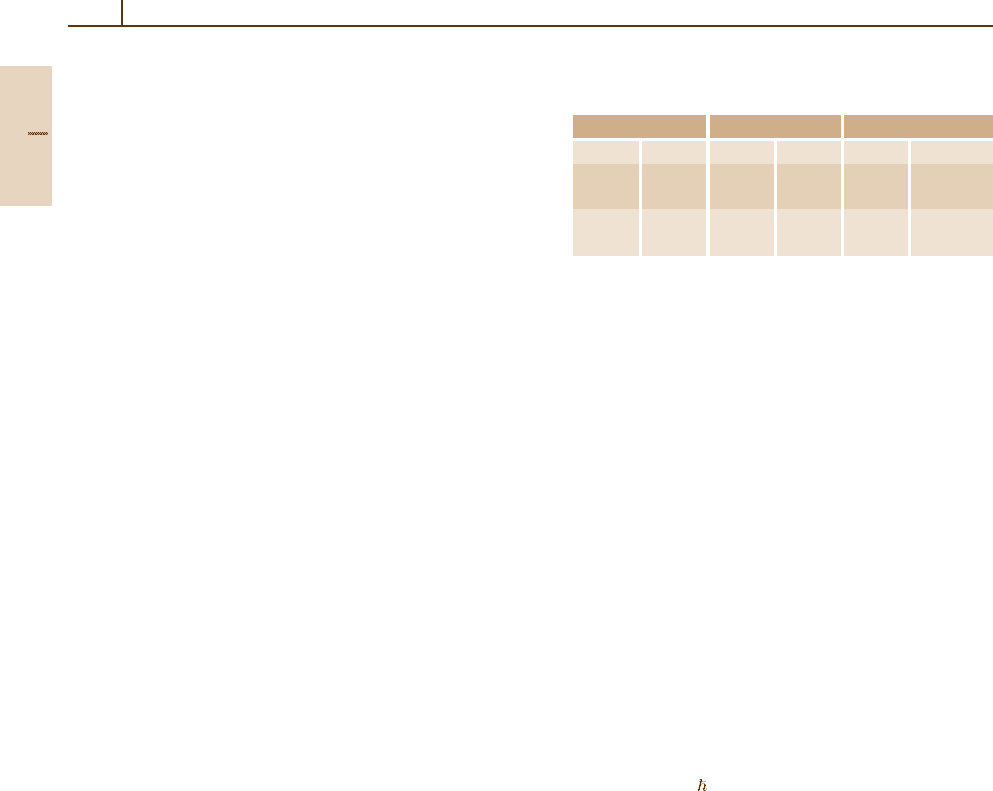
Table 49.1 Selection rules for the coupling between diabatic and adiabatic states of a diatomic quasimolecule (w = g, u;
σ =+, −)
Interaction
2S+1
Λ
(σ)
w
nomenclature Ω
(σ)
w
nomenclature
Configuration interaction ∆Λ = 0, ∆S = 0 ∆Ω =0
(electrostatic) g u, + − g u, + −
Spin–orbit interaction ∆Λ =0, ±1, ∆S = 0, ±1 ∆Ω = 0
g u, + − g u, + −
Radial motion ∆Λ = 0, ∆S = 0 ∆Ω = 0
g u, + − g u, + −
Rotational motion ∆Λ =±1, ∆S = 0 ∆Ω =±1
g u, + − g u, + −
Hyperfine interaction ∆Λ = 0, ±1, ∆S = 0, ±1 ∆Ω =0, ±1
g u, + − g u, + −
symmetry (C
∞v
or, for identical atoms, D
∞h
point sym-
metry in the adiabatic approximation). In the adiabatic
representation, the coupling is due to the elements of
the matrix D . They fall into two different categories:
those proportional to the radial nuclear velocity (coup-
ling by radial motion or radial coupling), and those
proportional to the angular velocity of rotation of the mo-
lecular axis (coupling by rotational motion or Coriolis
coupling).
In a diabatic representation, provided that the effect
of the D matrix is neglected, the coupling is due to the
parts of the interaction potential neglected in the defi-
nition of the diabatic Hamiltonian H
0
. In typical cases,
these parts are the electrostatic interaction between dif-
ferent electronic states constructed as certain electronic
configurations (H
0
corresponds to a self-consistent field
Hamiltonian); spin–orbit interaction (H
0
corresponds
to a nonrelativistic Hamiltonian); hyperfine interaction
(H
0
ignores the magnetic interaction of electronic and
nuclear spins as well as the electrostatic interaction be-
tween electrons and nuclear quadrupole moments). The
selection rules for the above interactions in the case
of two atoms are listed in Table 49.1 for two conven-
tional nomenclatures for molecular states: Hund’s case
(a),
2S+1
Λ
(σ)
w
and Hund’s case (c), Ω
(σ)
w
[49.3].
For molecular systems with more than two nuclei,
the selection rules cannot be put in a detailed form
since, in general, the symmetry of the system is quite
low. For the important case of three atoms, a general
configuration is planar (C
s
symmetry); particular con-
figurations correspond to an isosceles triangle if two
atoms are identical (C
2v
symmetry), to an equilateral
triangle for three identical atoms (D
3h
symmetry) or
to a linear configuration. For the last case, the selec-
tion rules are the same as for a system of two atoms.
Part D 49.2
746 Part D Scattering Theory
The selection rules for the dynamic coupling between
adiabatic states classified according to the irreducible
representations of the C
s
and C
2v
groups are listed in
Table 49.2.Inthistable,z and y refer to two modes of
the relative nuclear motion in the system plane, R
z
and
R
y
refer to two rotations about principal axes of iner-
tia lying in the system plane, and R
x
refers to a rotation
about the principal axis of inertia perpendicular to the
system plane.
Table 49.2 Selection rules for dynamic coupling between
adiabatic states of a system of three atoms
C
s
A
A
C
2v
A
1
B
1
A
2
B
2
A
A
1
z y, R
x
R
z
R
y
B
1
y, R
x
z R
y
R
z
A
A
2
R
z
R
y
z y, R
x
B
2
R
y
R
z
y, R
x
z
49.3 Single-Passage Transition Probabilities: Analytical Models
49.3.1 Crossing
and Narrow Avoided Crossing
of Potential Energy Curves:
The Landau–Zener Model
in the Common Trajectory
Approximation
The Landau–Zener model applies to a situation when
the effective adiabatic PEC cross or show a narrow
avoided crossing. The latter is defined by the condition
that the spacing between adiabatic PEC within a NAR is
much smaller than the spacing between adiabatic PEC
aw ay from the NAR. The cases of crossing and narrow
avoided crossing of adiabatic PEC can be considered
within a unified model since a narrow avoided crossing
of adiabatic PEC corresponds to a crossing of diabatic
PEC. Therefore, in both cases, one considers the cross-
ing of zero-order PES (adiabatic or diabatic) and the
interaction between them (dynamic or static). Ho wever,
the definition of transition probability is different for
crossing and avoided crossing.
In the framework of the Landau–Zener model [49.4–
6], the two zero-order PEC which cross at
a point Q
p
along a trajectory Q(t) are approx-
imated by functions linear in ∆Q = Q −Q
p
,and
the off-diagonal matrix element is assumed to be
a constant.
For the avoided crossing adiabatic PEC (crossing
diabatic PEC), the matrix H
jk
within a NAR is approxi-
mated as
H
11
(Q) = E
0
−F
1
(Q −Q
p
),
H
22
(Q) = E
0
−F
2
(Q −Q
p
),
H
12
(Q) = V = constant , (49.28)
from which the spacing between adiabatic PEC is
∆U =
(∆F)
2
(Q −Q
p
)
2
+4|V|
2
1/2
, (49.29)
with ∆ F =|F
1
−F
2
|.
The common trajectory is assumed to be a linear
function of t,
Q = Q
p
+v
p
t , (49.30)
where v
p
is the velocity of Q-motion at point Q
p
.
For this model, adiabatic wave functions on both
sides of the nonadiabaticity region (in the limits
−∞ < t < +∞) coincide with diabatic functions, but
their ordering is reversed. Explicitly,
ψ
1
= φ
1
; ψ
2
= φ
2
for t →−∞,
ψ
1
= φ
2
; ψ
2
=−φ
1
for t →+∞. (49.31)
The transition probability between pseudocrossing adi-
abatic curves for the Hamiltonian (49.28)andthe
trajectory (49.30) is given by the Landau–Zener formula
P
psc
12
= P
LZ
12
= exp
−2πζ
LZ
;
ζ
LZ
= V
2
/( ∆Fv
p
), (49.32)
where ζ
LZ
is the appropriate Massey parameter at the
pseudocrossing point. Note that for the LZ model, the
single-passage transition probability depends on one di-
mensionless parameter ζ
LZ
. A remarkable property of
the Landau–Zener model is that the probability P
LZ
12
is
givenby(49.26) for an arbitrary value of the exponent,
and not only for large ones when the probability is very
low.
With a change of the velocity from very low to very
high values, the transition probability varies from zero
to unity. In the near-adiabatic limit, ζ
LZ
1, the nuclei
preferentially move across single adiabatic PEC, while
in the sudden limit, ζ
LZ
1, they move across single
diabatic PEC. It is the latter property of the LZ transition
probability that allows one to interpret diabatic energies
H
11
and H
22
as the potentials which drive the nuclear
motion at high velocities.
Part D 49.3

Adiabatic and Diabatic Collision Processes at Low Energies 49.3 Single-Passage Transition Probabilities: Analytical Models 747
The region of applicability of the Landau–Zener
formula is determined by the condition that the e x-
tension of the region of nonadiabatic interaction ∆Q
should be small compared with the range a over which
potential curves deviate substantially from linear func-
tions. The condition ∆Q a actually implies the two
conditions [49.2]
2V/∆F a ,
(49.33)
and
2
v
p
/∆F
1/2
a . (49.34)
Clearly, the range parameter a does not enter the LZ
formula since it controls the behavior of adiabatic curves
away from the crossing point.
The constant velocity approximation (49.30)im-
poses yet another condition:
V µv
2
p
/2 . (49.35)
The actual application of (49.32) requires the specifi-
cation of V and v
p
for each particular trajectory Q(t).
For the case of avoided crossing between two poten-
tial curves of a diatom, V does not depend on the
trajectory and represents, according to Table 49.2,the
matrix element of the electrostatic interaction, spin–orbit
interaction or hyperfine interaction.
For crossing adiabatic PEC, the Landau–Zener
model assumes the following approximation for adia-
batic potentials and the dynamic coupling:
U
1
(Q) = E
0
−F
1
(Q −Q
c
),
U
1
(Q) = E
0
−F
2
(Q −Q
c
),
D
12
(Q) = D = constant , (49.36)
with the trajectory parametrization given by (49.30)
where v
p
is replaced by v
c
. Since the ordering of adia-
batic PEC for crossing and pseudocrossing is reversed
on one side of a NAR, the following relation exists be-
tween transition probabilities for the crossing case P
c
12
,
and the survival probability for the pseudocrossing case
1 − P
psc
12
:
P
c
12
= 1 − P
psc
12
, (49.37)
provided that D and v
c
in the crossing situation are
replaced by V and v
p
in the pseudocrossing situation.
Conditions (49.33)and(49.34)appliedtothecaseof
the dynamic coupling often imply that this coupling is
weak [49.2]. Therefore, (49.37) yields
P
c
12
=
2πD
2
∆Fv
c
. (49.38)
Usually, the matrix element D is related to the Coriolis
coupling, and it is proportional to the angular velocity of
rotation of the molecular frame at the crossing point Q
c
.
49.3.2 Arbitrary Avoided Crossing
and Diverging Potential
Energy Curves: The Nikitin Model
in the Common Trajectory
Approximation
The restrictions of narrow avoided crossing [(49.33)and
(49.34)fortheLZ model] are relaxed in a more gen-
eral model suggested by Nikitin [49.7]. This model uses
a more flexible exponential parametrization, instead of
the linear parametrization for diabatic matrix elements
(49.36).
In a diabatic basis, the model is formulated with the
Hamiltonian
H
11
(Q) =U
0
(Q)−∆ E/2+(A/2)cos 2ϑ exp(−αQ),
H
22
(Q) =U
0
(Q)+∆ E/2−(A/2)cos 2ϑ exp(−αQ),
H
12
(Q) =(A/2) sin 2ϑ exp(−αQ). (49.39)
The spacing between adiabatic PEC is
∆U = ∆E
1 −2cos2ϑ exp
−α
Q −Q
p
+exp
−2α
Q −Q
p
1/2
, (49.40)
where Q
p
is introduced instead of A via (49.21)and
(49.23). At the center of an NAR,whereQ = Q
p
,the
spacing between adiabatic PEC, ∆U
p
=∆U(Q
p
),is
∆U
p
= 2∆E sin ϑ. (49.41)
The common trajectory within the NAR is taken in
a form identical to (49.30)inwhichv
p
is now the
velocity of Q motion at the center of the coupling
region Q
p
.
For this model, adiabatic wave functions coincide
with diabatic functions before entering the coupling re-
gion (in the limit α(Q −Q
p
) 1), but after exiting the
coupling region [in the limit α(Q −Q
p
) −1] they are
linear combinations of the diabatic functions
ψ
1
(r;Q) = φ
1
(r), ψ
2
(r;Q) = φ
2
(r),
for α(Q −Q
p
) 1 ;
ψ
1
= φ
1
cos ϑ +φ
2
sin ϑ,
ψ
2
=−φ
1
sin ϑ +φ
2
cos ϑ,
for α(Q −Q
p
) −1 . (49.42)
The latter equation identifies the parameter ϑ that enters
into the definition of the diabatic Hamiltonian in (49.39)
Part D 49.3

748 Part D Scattering Theory
with the asymptotic value of the mixing angle θ (49.12)
for α(Q −Q
p
) −1.
The transition probability P
12
between adiabatic
PEC for the Hamiltonian (49.39) and the trajectory
(49.30)is
P
N
12
= exp(−πζ
p
)
sinh(πζ −πζ
p
)
sinh(πζ)
,
(49.43)
where ζ = ∆ E/( αv
p
) and ζ
p
= ζ sin
2
ϑ. With the
change in velocity from very low to very high values,
the transition probability varies from zero to cos
2
ϑ.As
ϑ changes from very small values to π, the pattern of
adiabatic potential curves changes from narrow to wide
pseudocrossing and ultimately to strong divergence.
Since the single-passage transition probability
(49.43) depends on two parameters, the Nikitin model
is more versatile than the Landau–Zener one.
In three limiting cases, ϑ 1,ζ1, ϑ =π/4, ζ ar-
bitrary, and ϑ arbitrary, ζ =0, (49.43) may be simplified.
In the first case, the diabatic Hamiltonian (49.39)be-
comes the Landau–Zener Hamiltonian (49.28). Also,
(49.43) reduces to a single exponential which gives the
LZ transition probability,
P
N
12
= P
LZ
12
= exp(−2πζ
p
), (49.44)
with ζ
p
identical to ζ
LZ
. The two conditions ϑ 1
and ζ 1 are equivalent to the two conditions (49.33)
and (49.34). In the second case (ϑ = π/4), the diabatic
Hamitonian reads
H
11
(R) = E
0
−∆E/2 ,
H
22
(R) = E
0
+∆E/2 ,
H
12
(R) = ( A /2) exp(−αQ). (49.45)
The transition probability in this case is given by the
Rosen–Zener–Demkov formula [49.8, 9]
P
RZD
12
=
exp(−πζ)
1 +exp(−πζ)
,ζ=∆ E/(
v
p
α) . (49.46)
In the third case (ζ = 0), also called the resonance
case since ∆E = 0, the transition probability reads
P
Res
12
= cos
2
ϑ. (49.47)
Equation (49.47) is a particular example of transitions
between initially degenerate states. This kind of tran-
sition occurs in the recoupling of angular momenta
in collisions of atoms possessing nonzero electronic
angular momentum [49.10].
For the general case, the nuclei preferentially mo ve
across single adiabatic PEC in the near-adiabatic limit,
ζ 1, while in the sudden limit, ζ 1, they move
across both diabatic PEC, unless the condition of narrow
avoided crossing, ϑ 1, is fulfilled.
49.3.3 Beyond the Common Trajectory
Approximation
The common trajectory approximation is valid when the
spacing between adiabatic PEC within an NAR is small
compared to the local kinetic energy of the nuclei. The
relaxation of this restriction is not unambiguous since
one should pass from a one-dimensional manifold (time
as a progress variable) to a multi-dimensional coordi-
nate (configuration space manifold). Only if the latter is
one-dimensional (a single coordinate as a progress vari-
able, as is the case for atom-atom collisions), one can
suggest a generalization of the common trajectory tran-
sition probability. We consider this case, taking R to be
such a single coordinate, and assume that the quantum
motion across the adiabatic PEC satisfies standard qua-
siclassical conditions [49.3]. For a two-state problem
with adiabatic potentials U
1
(R) and U
2
(R), the gen-
eral condition of the common trajectory apporximation
reads
E −
1
2
U
1
(R
p
) +U
2
(R
p
)
U
1
(R
p
) −U
2
(R
p
)
,
(49.48)
where E is the total (conserved) energy and R
p
is the
coordinate of the NAR center.
The quantum generalization of the expression for
the transition probability in the near-adiabatic condition,
(49.26), is given by the original Landau formula [49.4, 5]
P
12
= exp
−
2
Im
R
c
R
2µ
E −U
1
(R)
dR
−
R
c
R
2µ
E −U
2
(R)
dR
,
(49.49)
where µ is the reduced mass of the colliding atoms,
R
c
is the complex-valued coordinate of the crossing
of U
1
(R) and U
2
(R) and R is any value of the co-
ordinate in the classically accessible region of motion
of the nuclei. The nonadiabatic transition is local-
ized in the region of width ∆R = Im(R
c
) centered
at R
p
= Re(R
c
). Equation (49.49) becomes the com-
mon trajectory equation (49.26) under the condition
(49.48).
The quantum generalization of the LZ transition
probability can not be represented by an exact analyti-
cal expression though it is known that it depends on two
Part D 49.3

Adiabatic and Diabatic Collision Processes at Low Energies 49.4 Double-Passage Transition Probabilities and Cross Sections 749
parameters (and not on one, as in the case for the com-
mon trajectory approximation) [49.2]. A recommended
approximate expression for E > E
0
reads [49.11]
P
LZ
12
= exp
−2πζ
LZ
2
1+
1+
−2
p
1
160
p
(ζ
LZ
)
2
+0.7
1/2
,
(49.50)
where
p
=
µv
2
p
2V
∆F
2
√
|F
1
F
2
|
.
Equation (49.50) becomes the common trajectory
(49.32) under the condition
p
1; it turns out that the
latter condition may be less restrictive than the general
condition (49.48).
The quantum generalization of the Nikitin
transition probability is possible provided U
0
(R)
in (49.39) is given by an exponential func-
tion, U
0
(R) ≈ exp(−αR). The transition probability
reads [49.11]:
P
N
12
= exp(−πδ
p
)
sinh(πδ −πδ
p
)
sinh(πδ)
(49.51)
and depends on three parameters of the model (and not
two as is the case for the common trajectory approxi-
mation). These parameters enter into δ
p
and δ through
complicated contour integrals. If the general condition
of the common trajectory approximation, (49.48) , is ful-
filled, δ
p
and δ reduce to ζ
p
and ζ so that (49.51) becomes
(49.43).
More discussions of two-state models within and
beyond the common trajectory approximation can be
found elsewhere [49.2, 11–14].
49.4 Double-Passage Transition Probabilities and Cross Sections
49.4.1 Mean Transition Probability
and the Stückelberg Phase
In the case of an atomic collision, the set R shrinks into
a single coordinate R. If there is only one NAR over
the whole range of R, the colliding system traverses it
twice, as the atoms approach and then recede. In this
case, there are two different paths between the center
of the NAR, R
p
, and the turning points R
t1
and R
t2
on the adiabatic potential curves U
1
(R) and U
2
(R).
The double-passage transition probability P
12
is ex-
pressed via the single-passage transition probability P
12
,
the single-passage survival probability 1 − P
12
,andthe
Stückelberg interference term cos ∆Φ
12
[49.15],
P
12
= 2P
12
(1 − P
12
)(1 −cos ∆Φ
12
)
= 4P
12
(1 − P
12
) sin
2
(∆Φ
12
/2). (49.52)
The Stückelberg phase ∆Φ
12
/2 is expressed as the
phase difference ∆Φ
(0)
12
/2 which is accumulated during
the motion of a diatom from the center of the NAR to
the turning points, together with an additional phase φ
12
by
∆Φ
12
/2 = ∆Φ
(0)
12
/2 +φ
12
. (49.53)
Generally, (49.53) is valid provided ∆Φ
12
/2 1. For
transitions between electronic states of the same ax-
ial symmetry, the relative angular momentum of the
colliding atoms is conserved, and we have
∆Φ
(0)
12
/2 =
R
t1
R
p
2µE −
2
( +1)/R
2
−2µU
1
(r)
1/2
dR/
−
R
t2
R
p
2µE −
2
( +1)/R
2
−2µU
2
(r)
1/2
dR/ ,
(49.54)
where R
t1
and R
t2
are the turning points for adiabatic
motion on potential curves U
1
and U
2
, E is the total
energy. Once R
p
is chosen, ∆Φ
(0)
12
/2 is well-defined and
is independent of the dynamic details of a nonadiabatic
transition. On the other hand, P
12
and φ
12
do depend
on these details. In particular, for the models discussed
in Sect. 49.3, the velocity v
p
that enters into the Massey
parameter, is
v
p
=
2
µ
1/2
!
E −U
p
−
2
( +1)
2µR
2
p
"
1/2
,
(49.55)
where U
p
≈U
1
(R
p
) ≈U
2
(R
p
). As a function of E and ,
the double-passage transition probability is symmetric
with respect to the initial and final states.
Part D 49.4
750 Part D Scattering Theory
In many applications, one can use the mean transi-
tion probability P
12
, which is obtained from P
12
by
averaging over sev eral oscillations:
P
12
=2P
12
(1 − P
12
). (49.56)
The important limiting cases of the double-passage
Nikitin model are:
(i) Double-passage Landau–Zener–Stückelberg equa-
tion,
P
LZS
12
= 4exp
−2πζ
LZ
1 −exp
−2πζ
LZ
×sin
2
#
∆Φ
(0)
12
/2 +φ
LZS
12
$
,
(49.57)
where ζ
LZ
is given by (49.32), ∆Φ
(0)
12
/2by(49.54)
and the expression for φ
LZS
12
is available [49.2]. When
ζ
LZ
changes from zero to infinity,
%
P
LZS
12
&
passes through
amaximum,P
12
max
= 1/2, and φ
LZS
12
decreases
from π/4tozero.
(ii) Double-passage Rosen–Zener–Demkov equation:
P
RZD
12
=
sin
2
∆Φ
(0)
12
/2 +φ
RZD
12
cosh
2
(πζ/2)
.
(49.58)
where ζ is given by (49.46) and the expression for φ
RZD
12
is available [49.2]. Under certain conditions [49.2, 9],
the Stückelberg phase in (49.58) can be identified with
the phase accumulated during the motion of a diatom
from infinitely large distance to the turning points.
(iii) Double-passage equation for a resonance process
(∆E =0):
P
res
12
= sin
2
2ϑ
sin
2
∆Φ
12
/2
. (49.59)
The general resonance case (zero ener gy change,
∆E = 0) is also called an accidental resonance. For
the accidental resonance, the diagonal diabatic matrix
elements are not equal to each other. A particular case
of an accidental resonance is a symmetric resonance,
for which the diabatic matrix elements are the same. For
the Nikitin model, symmetric resonance corresponds to
ϑ = π/4, and (49.59) reads
P
symm
12
= sin
2
∆Φ
12
/2
. (49.60)
Equation (49.60) also follows from (49.58) in the limit
ζ → 0. Actually, (49.60) is valid for any symmetric
resonance case [not necessarily for the model Hamil-
tonians (49.39)and(49.45)] and for the arbitrary values
of the phase ∆Φ
12
/2. This phase can be identified
with ∆Φ
(0)
12
/2 from (49.54) provided R
p
is taken to be
infinitely large.
49.4.2 Approximate Formulae
for the Transition Probabilities
Several approximate formulae are available for P
12
in
the case where H
12
depends on time in a bell-shaped
manner, and ∆H = H
11
− H
22
can be represented as
ω +∆V, with ∆V also having a bell-shaped form.
Define
v =
1
+∞
−∞
H
12
(t) dt ;
w
0
=
1
+∞
−∞
H
12
(t) exp(iωt) dt ,
w =
1
+∞
−∞
H
12
(t) exp
(i/ )
t
0
∆H(t)dt
dt ,
u =
1
2
+∞
−∞
∆ V
12
(t) dt , (49.61)
and
S(t) = (1/ )
t
0
∆H
2
(t) +4H
2
12
(t)
1/2
dt . (49.62)
Then the various approximate formulae, as suggested by
different authors [49.2], read
P
12
∼
=
(w
0
/v)
2
sin
2
v, (49.63)
P
12
∼
=
sin
2
w, (49.64)
P
12
∼
=
w
2
0
u
2
0
+w
2
0
sin
2
(u
2
0
+w
2
0
), (49.65)
P
12
∼
=
+∞
−∞
H
12
(t) exp[iS(t)]dt/
2
, (49.66)
P
12
∼
=
sin
2
S
c
cosh
2
S
c
. (49.67)
In (49.67), S
c
and S
c
are the real and imaginary
parts of the complex quantity S
c
= S(t
c
) from (49.62).
The complex-valued time t
c
is found from
∆H
2
(t
c
) +4H
2
12
(t
c
) = 0 , (49.68)
under the condition that t
c
possesses the smallest im-
aginary part of all roots of this equation.
Part D 49.4
Adiabatic and Diabatic Collision Processes at Low Energies 49.5 Multiple-Passage Transition Probabilities 751
49.4.3 Integral Cross Sections
for a Double-Passage
Transition Probability
The quasiclassical inelastic integral cross section σ
if
for
the transition i → f is related to P
if
by
σ
if
=
π
µE
i
∞
0
P
if
d, (49.69)
where E
i
is the initial collision energy, E
i
= E−U
i
(∞).
Thecrosssectiondefinedby(49.69) typically shows the
following qualitative dependence on the collision ve-
locity: σ
if
increases rapidly with E
i
at low energies,
reaches a maximum and then slowly falls off at high
energies. The position of the maximum roughly cor-
responds to the energy E
i
= E
∗
i
at which the relevant
Massey parameter at the NAR center, ζ(R
p
),isofthe
order of unity. The conditions E
i
< E
∗
i
and E
i
> E
∗
i
cor-
respond to the near-adiabatic and strongly nonadiabatic
(also called diabatic) regimes, respectively.
In calculating σ
if
, one usually neglects the Stück-
elberg oscillating term and sets the upper limit in the
integral in (49.69)toavalue =
m
beyond which the
integrand begins to fall off quickly. Yet another sim-
plification is possible, in the framework of the impact
parameter approximation, when the relative motion of
atoms is described by a rectilinear trajectory R(t) with
constant velocity v and impact parameter b =
/µv:
R(t) =
b
2
+v
2
t
2
1/2
. (49.70)
For instance, for the Landau–Zener model
m
=
µvR
p
/ , and the cross section depends on one dimen-
sionless parameter γ = 2πV
2
/(∆F v) according to
σ
12
(γ) =2πR
2
p
1
0
exp(−γ/
√
x )
1−exp(−γ/
√
x )
dx
= 4πR
2
p
E
3
(γ) −E
3
(2γ)
, (49.71)
where E
3
(z) is the exponential integral.
For the symmetric resonance, the cross section reads
σ
if
(v) = 2π
∞
0
sin
2
!
∆Φ
Res
if
(b,v)
2
"
bdb ≈
π
2
b
2
m
(v) ,
(49.72)
where b
m
is found from the Firsov criterion [49.2]:
∆Φ
Res
if
b
m
,v
2
=
∞
b
∗
U
i
(R) −U
f
(R)
v
'
R
2
−b
2
m
dR =
2
π
.
(49.73)
The cross section in (49.71) first increases and then de-
creases with the collision velocity v, while that in (49.72)
slowly decreases with v.
49.5 Multiple-Passage Transition Probabilities
49.5.1 Multiple Passage in Atomic Collisions
In the case of atomic collisions, there is only one
nuclear coordinate R. If there exist several NAR on
the R-axis, those which are classically accessible (for
given total energy E and total angular momentum J)
can be traversed several times. In the semiclassical
approximation [49.16], the multiple-passage transition
amplitude A
if
for a given transition between inital state i
and final state f can be calculated as a sum of transi-
tion amplitudes A
L
if
, over all possible classical ways
L which connect these states, and which run along
a one-dimensional manifold R:
A
if
=
L
A
L
if
, (49.74)
where each A
L
if
can be expressed through the probabil-
ity P
L
if
and the phase Φ
L
if
by [49.13]
A
L
if
=
P
L
if
1/2
exp
iΦ
L
if
.
(49.75)
The net transition probability is then
P
if
=|A
if
|
2
(49.76)
=
L
P
L
if
+
L,L
P
L
if
P
L
if
1/2
cos
Φ
L
if
−Φ
L
if
.
The first sum runs over all different paths, and the sec-
ond (primed) over all different pairs of paths. The primed
sum usually yields a contribution to the transition prob-
ability which oscillates rapidly with a change of the
parameters entering into P
if
(i. e., E and J) and repre-
sents a multiple-passage counterpart to the Stückelberg
oscillations.
If the Stückelberg oscillations are neglected, P
if
is
equivalent to a mean transition probability P
if
:
P
if
=
L
P
L
if
. (49.77)
For one NAR, there are two equivalent paths, and P
(1)
if
=
P
(2)
if
= P
if
(1 − P
if
).Then(49.77) yields (49.56).
Part D 49.5
