Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics

Подождите немного. Документ загружается.

752 Part D Scattering Theory

49.5.2 Multiple Passage

in Molecular Collisions

For molecular collsions, (49.74)and(49.75) apply as

well. However, the manifold of R to which a trajec-

tory Q(t) belongs now comprises 3N −5 (for a linear

arrangement of nuclei) or 3N −6 (for a nonlinear ar-

rangement) degrees of freedom, where N is the number

of atoms in the system. The approximation (49.77)is

called, in the context of inelastic molecular collisions,

the surface-hopping approximation [49.17, 18]. Each

time a trajectory reaches an NAR, it bifurcates, and the

system makes a hop from one PES to another with a cer-

tain probability. Keeping track of all the bifurcations

and associated probabilities, one calculates P

along

apathL made up of different portions of trajectories

running across different PES. Because of the compli-

cated sequence of nonadiabatic events leading from the

initial state to the ﬁnal state, each P

is a complicated

function of different single passage transition probabil-

ities P

, and survival probabilities 1 − P

.Evenif

all P

are known in analytical form, the calculation of

P

 requires numerical computations to keep track of

individual nonadiabatic events [49.17].

The manifold R can be reduced in size if one treats

other degrees of freedom, besides electronic ones, on

the same footing. In this way one introduces adiabatic

vibronic (vibrational + electronic) states and adiabatic

vibronic PES, and considers nonadiabatic transitions

between them [49.19]. In the vibronic representation,

the formal theory remains the same; however its imple-

mentation is more difﬁcult since there are many more

possibilities for trajectory branching. Finally, under cer-

tain conditions, one can use a fully adiabatic description

of all degrees of freedom save one – the intermolecular

distance R. This approach provides a basis for the statis-

tical adiabatic channel model (SACM)ofunimolecular

reactions [49.20] where the receding fragments are scat-

tered adiabatically in the exit channels after leaving the

region of a statistical complex.

For a latest review of the theory of molecular nona-

diabatic dynamics, see [49.21] and papers in [49.22].

References

49.1 R. B. Bernstein (Ed.): Atom-Molecule Collision The-

ory: A Guide for the Experimentalist (Plenum, New

York 1979)

49.2 E. E. Nikitin, S. Ya. Unamskii: Theory of Slow Atomic

Collisions (Springer, Berlin, Heidelberg 1984)

49.3 L. D. Landau, E. M. Lifshitz: Quantum Mechanics

(Pergamon, Oxford 1977)

49.4 L. D. Landau: Phys. Z. Sowjetunion 1, 88 (1932)

49.5 L. D. Landau: Phys. Z. Sowjetunion 2, 46 (1932)

49.6 C. Zener: Proc. Roy. Soc. 137, 396 (1932)

49.7 E. E. Nikitin: Discuss. Faraday Soc. 33, 14 (1962)

49.8 N. Rosen, C. Zener: Phys. Rev. 40,502(1932)

49.9 Yu. N. Demkov: Sov. Phys. JETP 18,138(1964)

49.10 E. I. Dashevskaya, E. E. Nikitin: Quasiclassical ap-

proximation in the theory of scattering of polarized

atoms. In: Atomic Physics Methods in Modern Re-

search, Lecture Notes in Physics, Vol. 499, ed. by

K. Jungmann, J. Kowalski, I. Reinhard, F. Träger

(Springer, Berlin, Heidelberg 1997) p. 185

49.11 H. Nakamura: Nonadiabatic Transition: Concepts,

Basic Theories and Applications (World Scientiﬁc,

Singapore 2002)

49.12 M. S. Child: Semiclassical Mechanics with Molecular

Applications (Clarendon, Oxford 1994)

49.13 S. F. C. O’Rourke, B. S. Nesbitt, D. S. F. Crothers: Adv.

Chem. Phys. 103, 217 (1998)

49.14 E. S. Medvedev, V. I. Osherov: Radiationless Tran-

sitions in Polyatomic Molecules (Springer, Berlin,

Heidelberg 1994)

49.15 E. C. G. Stückelberg: Helv. Phys. Acta 5,369

(1932)

49.16 W. H. Miller: Adv. Chem. Phys. 30, 77 (1975)

49.17 S. Chapman: Adv. Chem. Phys. 82, 423 (1992)

49.18 J. C. Tully: Nonadiabatic dynamics. In: Modern

Methods for Multidimensional Dynamics Compu-

tations in Chemistry, ed. by D. L. Thompson (World

Scientiﬁc, Singapore 1998) p. 34

49.19 V. Sidis: Adv. At. Opt. Phys. 26, 161 (1990)

49.20 M. Quack, J. Troe: Statistical adiabatic channel

models. In: Encyclopedia of Computational Chem-

istry, Vol. 4, ed. by P. v. R. Schleyer, N. L. Allinger,

T. Clark, J. Gasteiger, P. A. Kollman, H. F. Schae-

fer III, P. R. Schreiner (Wiley, Chichester 1998)

p. 2708

49.21 A. W. Jasper, B. K. Kendrick, C. A. Mead, D. G. Truh-

lar: Non-Born–Oppenheimer chemistry: Potential

surfaces, couplings, and dynamics. In: Modern

Trends in Chemical Reaction Dynamics: Experiment

and Theory (Part I), ed. by X. Yang, K. Lui (World

Scientiﬁc, Singapore 2004) p. 329

49.22 A. Lagana, G. Lendvay (Eds.): Theory of Chemical

Reaction Dynamics (Kluwer, Dordrecht 2004)

Part D 49

753

Ion–Atom and

50. Ion–Atom and Atom–Atom Collisions

This chapter summarizes the principal features

of theoretical treatments of ion–atom and

atom–atom collisions. This is a broad topic

and the goal here is a general overview that

introduces the main concepts, terminology, and

methods in the ﬁeld. Attention will focus on

intermediate and high collision velocities, for

which the relative velocity between the projectile

and target is on the order of, or larger than,

the orbital speed of the electrons active in the

transition.

50.1 Treatment of Heavy Particle Motion ...... 754

50.2 Independent-Particle Models

Versus Many-Electron Treatments ......... 755

50.3 Analytical Approximations

Versus Numerical Calculations ............... 756

50.3.1 Single-Centered Expansion ........ 757

50.3.2 Two-Centered Expansion ........... 758

50.3.3 One-and-a-Half Centered

Expansion ................................ 758

50.4 Description of the Ionization Continuum 758

References .................................................. 759

Low energy collisions are treated in Chapt. 49.Charge

transfer reactions are treated in Chapt. 51. We will

emphasize therefore excitation and ionization tran-

sitions, and discuss charge transfer only as it is

interrelated with these transitions. The description of

these heavy particle collisions has many features in

common with electron and positron collisions with

atoms and ions (Chapts. 47 and 48) and this chap-

ter should be studied in parallel with those. There are

also chapters dealing with special phenomena in ion–

atom collisions: excitation at high collision energies

and the Thomas peak (Chapt. 57), electron emission

in high energy ion–atom collisions (Chapt. 53), and

alignment and orientation (Chapt. 46). Other chapters

deal with certain speciﬁc theoretical methods: contin-

uum distorted wave (CDW) approximations (Chapt. 52),

the binary encounter approximation (Chapt. 56), and

classical trajectory Monte Carlo (CTMC) techniques

(Chapt. 58). The emphasis of the present chap-

ter is coupled-states calculations of excitation and

ionization. There are several review articles and mono-

graphs [50.1, 2].

The collisions considered here involve a projectile

ion or atom and a target atom. The collision kinemat-

ics can be described in the lab frame, where the target

atom is assumed to be initially at rest and the collision

energy is the kinetic energy of the projectile when it is

far from the target prior to the collision, or in the cen-

ter of mass frame. The primary quantities of interest are

the cross sections for producing various ﬁnal states of

the system for given initial states of the target and pro-

jectile. The total cross sections depend on the initial and

ﬁnal quantum state of the target and projectile and on

the collision energy. Let A denote the projectile atom or

ion with ionic charge q,andB denote the target atom.

Let A

∗

and B

∗

denote excited states. Some examples of

processes for which the cross section is of interest are

+ B →











)

∗

+ B , projectile excitation

+ B

∗

, target excitation

+ B

+ e

−

, target single ionization

(q+1)+

+ B+ e

−

, projectile single ionization

(q−1)+

+ B

, single e

−

charge transfer .

For a multi-electron collision system, combinations of

the above quantities are possible. A few representative

examples are

+ B →











+ B

+ 2e

−

, target double ionization

+ (B

)

∗

+ e

−

, target excitation-

ionization

(q−1)+

+ (B

)

∗

, transfer-excitation

(q−1)+

+ B

+ e

−

, transfer-ionization .

Part D 50

754 Part D Scattering Theory

For each of these processes, the projectile and/or tar-

get can be initially in excited states. A class of ion–atom

collisions that has received much theoretical attention

because of the relative simplicity is the one where the

projectile ion is initially bare, with charge q = Z

,the

projectile nuclear charge. One can also consider various

differential cross sections: differential in the projectile

scattering angle, in the energy and angle of emission

of ionized electrons, in recoil momentum of the tar-

get, etc.

Theoretical calculations of these cross sections

can be classiﬁed according to the approximations

and/or methods used. We will discuss four such clas-

siﬁcations: treatment of the heavy particle motion,

independent particle model (IPM) versus inclusion

of correlation in multi-electron systems, analytical

approximations (PWBA, SCA, Glauber, etc.) versus

numerical methods (such as coupled-states) for ob-

taining cross sections, and treatments of the ionization

continuum.

50.1 Treatment of Heavy Particle Motion

Only at very low energies must the motion of the nuclei

be described quantum mechanically. At the interme-

diate and high collision velocities considered here the

semiclassical approximation, in which the motion of

the nuclei can be described classically and only the

electrons need be described by quantum mechanical

wave functions, is accurate [50.3]. The projectile nu-

cleus then moves on a predetermined classical path. At

high collision energies this path can often be taken to

be a straight line path with constant speed. At some-

what lower energies the deﬂection and change in speed

of the projectile due to the projectile–target interaction

is often incorporated [50.4–6]. The Coulomb trajec-

tory due to the nucleus–nucleus interaction can be

used, and the screening effects of the projectile and

target electrons can be included. For a bare positive

ion projectile, the Coulomb trajectory effects increase

the distance of closest approach for a given impact

parameter and reduce the projectile speed in the interac-

tion region. Projectile trajectory effects are particularly

strong for projectiles less massive than protons (pos-

itive or negative muons [50.7], for example). The

semiclassical approach with trajectory effects has even

been used for electron impact excitation and ioniza-

tion [50.7]. Coulomb trajectories are also important

when small impact parameter collisions are consid-

ered. The recoil of the target nucleus can also be

treated classically and this recoil can affect the cross

sections [50.8–10].

In the semiclassical approximation, the vector

R(b, t) that locates the projectile relative to the target nu-

cleus is a function of the impact parameter b and time t.

The speciﬁc functional dependence is determined by

the trajectory being used. For a straight line, constant

velocity v path, R = b+ vt. For the case of a bare pro-

jectile ion and a one-electron target, the time-dependent

projectile–target interaction is given by

V(b, t) =

−Z

|r− R(b, t)|

R(b, t)

(50.1)

where Z

and Z

are the projectile and target nuclear

charges and r is the position vector of the electron rel-

ative to the target nucleus. If the collision calculation

starting from (50.1) is done exactly the nuclear repulsion

term Z

/R(b, t) does not involve the electronic

coordinates and makes no contribution to total cross

sections for anything other than elastic scattering. This

term makes a nonzero contribution in an approximate

calculation, such as a ﬁrst-order perturbation theory cal-

culation with nonorthogonal initial and ﬁnal states, and

this is a defect of such calculations.

A deﬁciency of the semiclassical approximation as

described above is that, since a predetermined classical

path is used, there is no coupling between the energy

and momentum given to the target electron and that lost

by the projectile. A simple improvement, in cases where

the energy lost by the projectile when the target transi-

tion occurs is an appreciable fraction of its total energy,

is to use some average of the projectile’s initial and ﬁnal

speeds as the asymptotic projectile speed. This results

in a projectile trajectory that depends on the cross sec-

tion being calculated. This lack of coupling between the

projectile motion and the states of the electrons can be

a particular deﬁciency when cross sections differential in

the scattering angle Θ of the projectile are computed. If

the collision energy is large and the projectile is scattered

primarily by the static potential of the target, a classical

treatment of the scattering can be used to relate b to Θ.

Even when straight line, constant speed projectile paths

are used to calculate the transition probabilities, differ-

ential cross sections can be extracted by relating b to Θ.

At lower energies, where the de Broglie wavelength of

Part D 50.1

Ion–Atom and Atom–Atom Collisions 50.2 Independent-Particle Models Versus Many-Electron Treatments 755

the projectile is not small compared with the range of

the interaction, eikonal methods can be used to convert

impact parameter dependent probabilities to differential

cross sections [50.11–13]. A particularly striking exam-

ple where there is strong coupling between the projectile

motion and the ﬁnal quantum state of the electron is

proton impact single and double ionization of helium

differential in the projectile scattering angle [50.14, 15].

The projectile can be deﬂected by interaction with the

target nucleus. In this case the projectile scattering angle

can be related to the impact parameter by the equations

of classical mechanics, and the projectile can be scat-

teredbyupto180

◦

as b is decreased to zero. But the

projectile can also be scattered by a close interaction

with a target electron, and the kinematics then can be

quite different. Such an interaction has a low probability

for scattering the projectile to a large angle. Classically,

from energy and momentum considerations, the maxi-

mum angle through which a proton can be scattered by an

electron initially at rest is about 0.5 mrads; and if the pro-

ton is scattered through 0.5 mrads, the electron acquires

large energy and momentum. The combined effects of

both projectile scattering mechanisms are difﬁcult to

treat in a semiclassical model [50.16].

50.2 Independent-Particle Models Versus Many-Electron Treatments

In the semiclassical impact parameter method, as de-

scribedinSect.50.1, for a single electron collision

system one has to calculate a single particle wave func-

tion and from it single-electron transition amplitudes.

A multi-electron collision problem can be treated as an

effective single-electron problem if only one projectile–

electron interaction is considered and the other electrons

merely provide an effective single-particle potential in

which the active electron moves.

In an independent particle model (IPM), the

electron–electron interactions are replaced by effective

single-electron potentials. Since the projectile–target in-

teraction is a sum of single-electron interactions, the

many-electron collision problem reduces to an uncou-

pled set of single electron problems. Their solution at

each impact parameter gives single electron transition

amplitudes a

and transition probabilities ρ

=|a

Cross sections for multi-electron transitions can still be

calculated by combining the single-electron amplitudes

in an appropriate way [50.17, 18]. In doing this, it is im-

portant to distinguish between inclusive and exclusive

processes. For an inclusive cross section, one ﬁnal or-

bital occupancy, or a few ﬁnal orbital occupancies, is

speciﬁed, but the ﬁnal states of the remaining electrons

are not speciﬁed and all possibilities are summed over.

For a totally exclusive process, all ﬁnal orbital occu-

pancies are speciﬁed. For example, consider a p+ Ne

collision. For the inclusive cross section for K-shell va-

cancy production, at least one K-shell vacancy in the

ﬁnal state is speciﬁed. The other electrons could remain

in their original orbitals, there could be two K-shell va-

cancies, the K-shell vacancy could be accompanied by

any number of L-shell vacancies, etc., and all these pos-

sible ﬁnal states are summed over. An example of an

exclusive cross section is the cross section for produc-

ing a single K-shell vacancy with the speciﬁcation that

the ﬁnal state of the target have no additional vacancies.

In calculating inclusive cross sections from single-

electron transition amplitudes in an IPM it is important to

take proper account of time-ordering and Pauli exclusion

effects, as well as all multi-electron processes that lead to

the speciﬁed ﬁnal state. Again using the p+ Ne collision

example, a two-electron process that leads to a K-shell

vacancy is for the projectile to ﬁrst ionize an L-shell

electron, and then in the same collision to excite a K-

shell electron into the L-shell hole just produced. But

the K-shell electron must have the same spin component

as the L-shell electron that was removed, and the K to L

excitation can occur only after the L-hole has been made.

This can lead to correlations among the single-electron

amplitudes that have been called Pauli correlations or

Pauli blocking effects.

For a totally inclusive process where only one ﬁnal

occupancy is speciﬁed, all the multi-electron contri-

butions cancel in any IPM and the probability for

producing, for example, a hole in the initially occupied

orbital labeled 1, without any other speciﬁcation of ﬁnal

state orbital occupancies, is given by



k<N

, (50.2)

where k runs over the unoccupied bound orbitals of the

target, the bound orbitals of the projectile, and the con-

tinuum orbitals. This expression says that the inclusive

probability of producing a hole in the initially occu-

pied orbital 1 is given by the sum of the probabilities

of exciting an electron from this orbital to any initially

unoccupied orbitals of the projectile–target system. The

Part D 50.2

756 Part D Scattering Theory

cross section is then exactly the same as if only a sin-

gle target electron were interacting with the projectile.

However, for an inclusive process in which two vacan-

cies in orbitals of the same spin are speciﬁed in the ﬁnal

state, say orbitals 1 and 2, then the probability of produc-

ing this ﬁnal state is not the product of the independent

probabilities of producing a vacancy in orbital 1 and in

orbital 2 [50.17, 18]. The correlation produced by an-

tisymmetry destroys the independence of probabilities

for this process. Speciﬁc expressions, and also a dis-

cussion of how to derive the correct expressions to use

for any particular inclusive process, can be found in

the literature [50.17–19]. If these Pauli correlations are

neglected, and products of independent single-electron

transition probabilities are used, then the distribution of

multiple vacancies within a shell, such as the L-shell,

are given in terms of a binomial distribution [50.20–22].

The IPM treatment is inadequate if electron correla-

tion plays an important role in the collision. One notable

set of examples is two-electron transitions in which the

projectile–target interaction is weak, such as at high col-

lision energies. It is useful to characterize multi-electron

transitions as being either externally or internally in-

duced [50.23]. In an externally induced two-electron

process, the projectile interacts with both electrons and

induces the transition of each. In the internal process,

energy is transferred to just one electron; this energy is

then shared with the other electron through the internal

action of the correlating electron–electron force.

Consider double ionization. At sufﬁciently high

energies, the external reaction has an amplitude pro-

portional to Z

. To lowest order, the reaction proceeds

through two consecutive ﬁrst-order Born collisions,

perhaps more correctly described as a two-particle

second-order Born collision. This is called a two step

mechanism, TS2. The internal reaction amplitude, again

at sufﬁciently high energies, is proportional to Z

; one

ﬁrst-order Born reaction initiates the process. The shar-

ing of energy with the second electron can be thought of

in two ways. If the ﬁrst electron leaves without interact-

ing with the second, there is a change in the screening

that can be thought of as being responsible for shaking

the second electron off. The main role of the electron–

electron force here is to introduce correlation into the

initial ground state wave function. A second way for

both electrons to be ionized is for the ﬁrst electron to

strike the second on the way out. This has been var-

iously called interception or TS1 [50.21, 24–26]. The

role of the electron–electron force here is to introduce

correlation into the ﬁnal two-electron wave function.

At asymptotic energies the ﬁrst Born term will eventu-

ally dominate, and the internal correlated mechanism

is solely responsible for double ionization. At lower

energies, the external and internal amplitudes are of

the same order, and thus they interfere. The interfer-

ence produces terms in the transition probability that are

proportional to odd powers of Z

, and therefore pro-

duces a cross section that changes when the sign of the

projectile charge changes. One example is the double

ionization of helium in the MeV/amu collision energy

region, where antiprotons (Z

=−1) produce a double

ionization cross section a factor of two larger than that

for protons (Z

=+1) around 1 MeV/amu [50.25,26]. It

is possible to account for electron correlation directly by

putting the electron-electron interaction into the Hamil-

tonian and solving for the many-electron correlated wave

function of the collision system. In coupled-states cal-

culations (Sect. 50.3), this approach is computationally

intractable if more than a few coupled channels are

important, which is usually the case at intermediate col-

lision energies; but some full electron calculations have

been carried out [50.27–31]. In low-energy collisions

where molecular basis expansions are appropriate, only

a few channels can be important, i. e., those involved in

potential curve crossings or near crossings, and full elec-

tron calculations are more feasible. Some alternatives to

full electron quantum calculations have been developed,

such as the independent event model [50.32], classi-

cal dynamics calculations (Chapt. 58), time-dependent

Hartree–Fock (TDHF) [50.33, 34], and the forced im-

pulse method (FIM) [50.25, 26]. The FIM divides the

collision time into short sequential segments such that

an impulse approximation is forced to be valid. The sys-

tem is allowed to collapse back into a fully correlated

eigenstate at the end of each segment, but the electrons

propagate independently during each segment.

50.3 Analytical Approximations Versus Numerical Calculations

There is a wide variety of techniques used for computing

cross sections for ion–atom and atom–atom collisions.

One class uses approximate analytical methods. The ex-

pressions and the wave functions that enter into them

may be sufﬁciently complicated that they must be eval-

uated on a computer, but they can be written down as

Part D 50.3

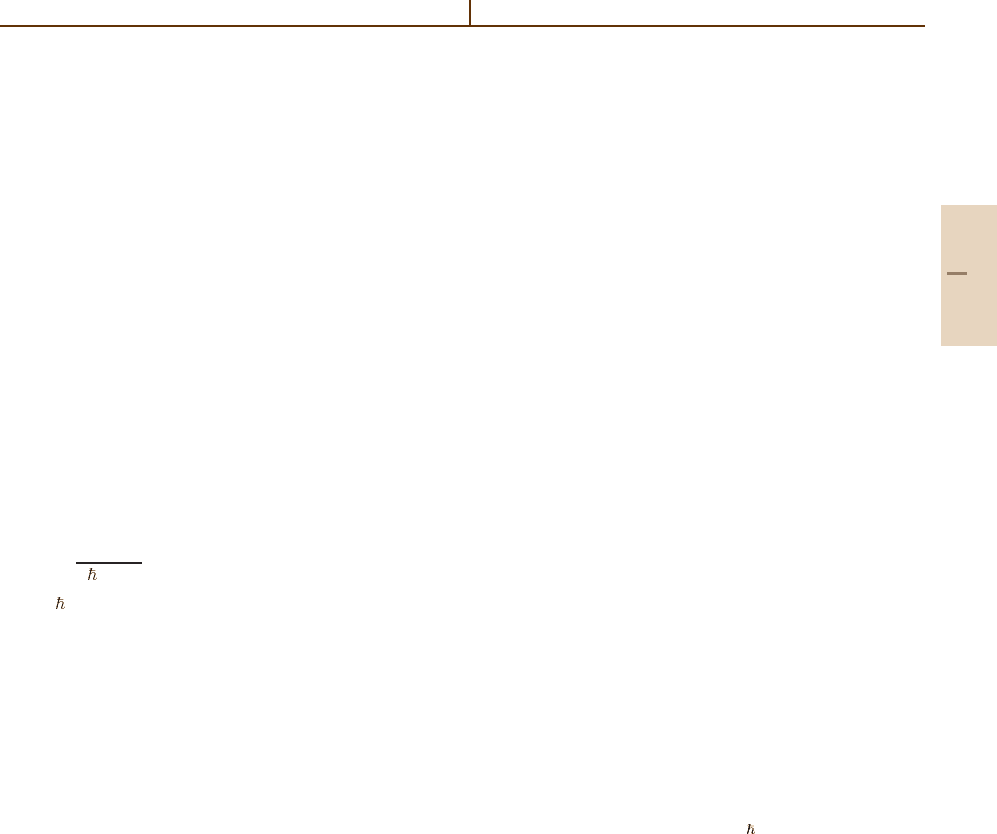
Ion–Atom and Atom–Atom Collisions 50.3 Analytical Approximations Versus Numerical Calculations 757

closed form expressions. One important example is the

ﬁrst Born approximation, in which the projectile–target

interaction is treated in ﬁrst-order. Hence, the ﬁrst Born

approximation is most accurate for weak interactions,

for example for small projectile charge and large colli-

sion energy. The ﬁrst Born approximation is commonly

expressed in either of two forms: the plane wave Born

approximation (PWBA) [50.35], where the projectile

nuclear motion wave function is taken to be a plane

wave, or the semiclassical approximation (SCA) [50.3]

which is an impact parameter approach that uses a clas-

sical path for the projectile motion. At the high collision

velocities where the ﬁrst Born approximation is accu-

rate, and for projectiles that are at least as massive as

a proton, the PWBA and SCA give identical results.

Since it is based on ﬁrst-order perturbation theory, the

ﬁrst Born approximation only requires computation of

the matrix element of the projectile interaction between

initial and ﬁnal state wave functions. For example, the

ﬁrst Born transition amplitude for a bare ion (charge Z

mass M) incident on a one electron target is

2MZ



∗

(r) e

iK·r

(r) d

r , (50.3)

where K is the momentum transfer vector and φ

are the initial and ﬁnal state wave functions. For

a hydrogenic system, analytical expressions for the

PWBA amplitudes for bound–bound transitions can be

derived [50.36] and for bound–continuum transitions

(ionization) the cross section can be expressed in terms

of a two-dimensional integral over energy and momen-

tum transfer, where the integrand is given by a simple

analytical expression [50.37]. First Born calculations

are also carried out with relativistic wave functions; rel-

ativistic target wave function effects are important for

the inner shells of heavy atoms [50.38].

There is a number of other approximate methods

that lead to simple analytic expressions, such as the

Glauber approximation [50.39–41], continuum distorted

wave (CDW) and eikonal methods (Chapt. 52), the bi-

nary encounter approximation (BEA, Chapt. 56), and

second Born calculations [50.42]. A difﬁculty with all

these methods is that they do not admit to a sequence

of successive improvements; there is no procedure for

systematically driving them to convergence.

One class of approximation methods very widely

used for inner shell processes, such as inner shell va-

cancy production, is based on perturbed stationary state

(PSS) methods. One variation is the energy loss and

Coulomb deﬂection effects perturbed stationary state

approximation with relativistic correction (ECPSSR)

theory, developed originally by Brandt and co-workers

and since extended and applied by others [50.43, 44].

This approximation involves procedures for correcting

the ﬁrst Born approximation. It is quite successful in

ﬁtting K-, L-, and M-shell vacancy production cross

sections.

Another approach is to calculate the electronic wave

function for the collision system by expanding it in

some basis set [50.45, 46]. This procedure is called

the coupled-channels, coupled-states, or close-coupling

method. It is convenient to diagonalize the target and

projectile systems in the chosen basis to produce matrix

eigenfunctions for the target and projectile. Putting this

expansion into the time-dependent Schrodinger equa-

tion leads to a set of coupled ﬁrst-order equations for the

time-dependent expansion coefﬁcients. This set of equa-

tions is solved subject to the boundary condition that

long before the collision, the expansion coefﬁcient for

the initial state wave function is unity and all other coef-

ﬁcients are zero. Then the expansion coefﬁcients a long

time after the collision give the transition amplitudes for

transitions into those states.

Several types of expansions are used. The notation

appropriate to a single-electron problem will be used for

simplicity.

50.3.1 Single-Centered Expansion

In the single-centered expansion [50.47, 48], the wave

function is expanded in a set of target centered basis

functions. Diagonalization of the target Hamiltonian in

this basis yields a set of target eigenfunctions φ

(r) and

energies E

. The expansion of the time-dependent wave

function for the collision system is then

(r, b, t) =



(b, t) e

−i(E

−E

)t/

(r). (50.4)

If the electron is initially in the target state i, the initial

boundary condition is a

(b, −∞) = δ

. The expansion

coefﬁcients at times long after the collision, a

(b, +∞),

give the transition amplitudes for transitions from target

state i to j. Ionization probabilities and the description

of the ionization continuum will be described in the next

section. It will sufﬁce to say here that some of the φ

(r)

represent ionized states and account for transitions that

leave the electron no longer in a target bound state. This

single centered expansion does not directly allow for

calculation of charge transfer amplitudes. However, it

has been shown that if the number of angular momenta

included in the set of φ

(r) is large enough, the basis

can accurately describe electron loss from the target

Part D 50.3

758 Part D Scattering Theory

bound states even in cases where the charge transfer

probability is large [50.47, 48]. If the charge transfer

amplitude is small, it can be extracted from ψ

(r, b, t)

by use of a ﬁrst-order T-matrix expression of the form

(b, +∞) =



(r− R)



U(r, R)



(r, b, t)



(50.5)

where φ

is a projectile state eigenfunction and U(r, R)

is the projectile–target interaction [50.49, 50].

50.3.2 Two-Centered Expansion

In a two-centered expansion [50.45,46,51–54], the time-

dependent wave function for the collision system is

expanded in two sets of functions: a set of eigenfunc-

tions centered on the target φ

(r) and a set of projectile

centered eigenfunctions φ

(r− R),

(r, b, t) =



(b, t)

×exp



−i(E

− E

)t/



(r)



(b, t) exp

[

−i(E

− E

)t/

]

×exp

[

i p· r/

]

(r− R). (50.6)

Here exp

[

i p· r/

]

is an electron translation factor that

accounts for the momentum p that the electron has rela-

tive to the target when it moves with the projectile. The

energies E

also contain the kinetic energy in the target

frame that the electron has when it moves with the pro-

jectile. The problem of electron translation factors when

a two centered molecular basis is used instead of the

atomic basis has been extensively addressed [50.45,46].

The coefﬁcients a

(b, +∞) and a

(b, +∞) are the

transition amplitudes for transitions into target and pro-

jectile states. The two-centered expansion allows for

charge transfer amplitudes to be calculated directly and

is capable of an accurate description of the electron ﬂux

loss from the target due to charge transfer, but the com-

putational difﬁculty is signiﬁcantly greater. It is difﬁcult

in practice to include enough basis functions for con-

vergence. Also, computational linear dependence can

arise if the projectile and target are close because the

projectile-centred basis set can become nearly identical

to the target-centred basis set.

Calculations have also been done with a triple-

centered expansion [50.55,56]. Bound atomic states are

centered on each nucleus and on a third center (the center

of charge) in order to simulate the molecular character of

slow collisions. The orbitals on this third center represent

the united-atom character of the wave function.

50.3.3 One-and-a-Half Centered

Expansion

To account for ﬂux loss from the target region due

to charge transfer, while retaining the computational

efﬁciency of the single-centered expansion, a hybrid

method called the one-and-a-half centered expansion

(OHCE) was developed [50.57]. It is of the same form as

the two-centered expansion except that the coefﬁcients

(b, t) of the projectile-centered states have predeter-

mined rather than variable time dependence. The time

dependence of the a

(b, t) must be such that the a

are all zero as t →−∞,andast →+∞ they be-

come constants that are identiﬁed as the charge transfer

amplitudes. This ansatz greatly reduces the computa-

tional cost of propagating the coupled equations forward

in time, but the projectile-centered functions are still

present to allow explicitly for charge transfer channels

at large times. At intermediate times, when the pro-

jectile and target separation is within the range of the

target-centered basis, the target-centered part of the ex-

pansion, if enough basis functions are used, is sufﬁcient

to describe the time dependence of ψ

(r, b, t) and the

projectile-centered part of the expansion is redundant.

The OHCE has been applied to several collision systems

with good success [50.58].

50.4 Description of the Ionization Continuum

In ion–atom and atom–atom collision calculations de-

scription of the ionization continuum presents particular

difﬁculties. For hydrogenic systems, the exact con-

tinuum wave functions are known analytically, and

these may be used in analytic approximations such

as the PWBA. For nonhydrogenic systems, screened

hydrogenic wave functions or numerical wave func-

tions computed from some local effective potential,

such as the Hartree–Fock–Slater approximation, can

be used [50.59]. But for coupled states calcula-

tions, that involve expansion of the system wave

function in terms of a discrete set of functions,

some discretization of the continuum must be per-

formed.

Part D 50.4

Ion–Atom and Atom–Atom Collisions References 759

A simple procedure for generating a discrete rep-

resentation of the continuum is to diagonalize the

target (or projectile) Hamiltonian in a ﬁnite basis of

square integrable basis functions. Some commonly used

basis functions are Sturmian [50.45, 46], Gaussian,

or Slater-type orbitals. This diagonalization produces

a set of discrete matrix eigenvalues and eigenvectors,

called pseudostates. For a one-electron or effective

one-electron system, the exact energy spectrum of the

Hamiltonian consists of an inﬁnite set of discrete bound

states and an ionization continuum and the interpre-

tation of the pseudostates is straightforward. The N

matrix eigenvalues below the ﬁrst ionization threshold

represent the bound states. By the Hylleraas–Undheim

Theorem, they are upper bounds to the ﬁrst N exact

energies (Sect. 11.2.1). The matrix eigenvectors with

positive eigenvalues provide a discrete representation

of the ionization continuum [50.60]. Each pseudostate

is accurately proportional to the exact continuum wave

function at the pseudostate energy for values of r out

to the range of the basis. The proportionality con-

stant gives the energy width of the pseudostate – the

energy region of the continuum represented by that

pseudostate [50.49,50]. These widths are approximately

equal to the energy spacing between pseudostates. The

pseudostates represent the continuum in the sense that

the total ionization cross section is equal to the sum

of the continuum pseudostate cross sections. Coupled-

states calculations have also been carried out with wave

packets constructed at discrete energies from the exact

continuum wave functions [50.61]. What all these dis-

cretization methods do is to provide a quadrature rule

for evaluating the integration over the energy of the ion-

ized electron. Differential cross sections, differential in

the ionized electron’s energy, have also been extracted

from discretized continuum calculations [50.62–65].

The situation is more complex for two-electron or

multi-electron systems. The energy spectrum of a two-

electron atom consists of an inﬁnite set of bound states,

an inﬁnite set of overlapping single ionization con-

tinua that correspond to different residual ion states,

and overlapping the higher energy part of these sin-

gle ionization continua, a double ionization continuum

where both electrons are unbound. The exact wave

function for two electrons in the continuum of an ion

is not known, but there are a number of approximate

forms [50.66–68]. The interpretation of two electron

pseudostates is also complicated. For energies below

the second single ionization threshold the energy of

a pseudostate clearly identiﬁes whether it represents

a bound state or an ionized state. But in the energy region

where there are overlapping continua there are ambi-

guities. For example, a pseudostate with energy above

the double ionization threshold can represent a doubly

ionized state, a singly ionized state of the same total

energy, or some admixture of the two. A method has

been developed to solve this pseudostate interpretation

problem [50.25, 26].

References

50.1 B. H. Bransden: Atomic Collision Theory (Benjamin-

Cummings, Reading 1983)

50.2 J. S. Briggs, J. H. Macek: Adv. At. Mol. Opt. Phys. 28,

1 (1991)

50.3 J. M. Hansteen: Phys. Scr. 42, 299 (1990)

50.4 G. L. Swafford, J. F. Reading, A. L. Ford, E. Fitchard:

Phys. Rev. A 16, 1329 (1977)

50.5 A. Jakob, F. Rösel, D. Trautmann, G. Bauer: Z. Phys.

A 309, 13 (1982)

50.6 W. Fritsch: J. Phys. B 15, L389 (1982)

50.7 M. H. Martir, A. L. Ford, J. F. Reading, R. L. Becker:

J. Phys. B 15, 1729 (1982)

50.8 P. A. Amudsen: J. Phys. B 11, 3179 (1978)

50.9 M. Kleber, K. Unterseer: Zeit. Phys. A 292, 311 (1979)

50.10 F. Rösel, D. Trautmann, G. Bauer: Nucl. Instrum.

Methods 192, 42 (1983)

50.11 B. H. Bransden, C. J. Noble: Phys. Lett. 70A,404

(1979)

50.12 J. M. Wadehra, R. Shakeshaft: Phys. Rev. A 26, 1771

(1982)

50.13 R. Gayet, A. Salin: Nucl. Instrum. Methods B56/57,

82 (1991)

50.14 A. Salin: J. Phys. B 24, 3211 (1991)

50.15 L. Meng, R. E. Olson, R. Dörner, J. Ullrich,

H. Schmidt-Böcking: J. Phys. B 26, 3387 (1991)

50.16 X. Fang, J. F. Reading: Nucl. Instrum. Meth. B53,

453 (1991)

50.17 J. Reinhardt, B. Muller, W. Greiner, G. Soff: Phys.

Rev. Lett. 43, 1307 (1979)

50.18 J. F. Reading, A. L. Ford: Phys. Rev. 21,124(1980)

50.19 R. L. Becker, A. L. Ford, J. F. Reading: Phys. Rev. A

29, 3111 (1984)

50.20 J. H. McGuire, P. Richard: Phys. Rev. A 8, 1874 (1973)

50.21 J. H. McGuire: Adv. At. Mol. Opt. Phys. 29,217

(1991)

50.22 Yu S. Sayasov: J. Phys. B 26, 1197 (1993)

50.23 J. F. Reading, A. L. Ford: Comments At. Mol. Phys.

23, 301 (1990)

50.24 J. H. McGuire: Phys. Rev. Lett. 49, 1153 (1982)

50.25 J. F. Reading, A. L. Ford: J. Phys. B 20, 3747 (1987)

Part D 50

760 Part D Scattering Theory

50.26 T. Bronk, J. F. Reading, A. L. Ford: J. Phys. B 31,2477

(1998)

50.27 W. Fritsch, C. D. Lin: Phys. Rev. A 41, 4776 (1990)

50.28 L. F. Errea, L. Mendez, A. Riera: Phys. Rev. A 27, 3357

(1983)

50.29 F. Martin, A. Riera, M. Yanez: Phys. Rev. A 34,4675

(1986)

50.30 H. A. Slim, B. H. Bransden, D. R. Flower: J. Phys. B

26, 159 (1993)

50.31 K. Moribayashi, K. Hino, M. Matsuzawa, M. Kimura:

Phys. Rev. A 44, 7234 (1991)

50.32 D. P. Marshall, C. LeSech, D. S. F. Crothers: J. Phys.

B 26, L219 (1993)

50.33 J. D. Garcia: Nucl. Instrum. Methods A240, 552

(1985)

50.34 W. Stich, J. J. Lüdde, R. M. Driezler: J. Phys. B 18,

1195 (1985)

50.35 E. Merzbacher, H. W. Lewis: Encyclopedia of Phys-

ics, Vol. 34 (Springer, Berlin, Heidelberg 1958) p. 166

50.36 D. R. Bates, G. Grifﬁng: Proc. Phys. Soc. A 66,961

(1953)

50.37 O. Benka, A. Kropf: At. Data Nucl. Data Tables 22,

219 (1978)

50.38 M. H. Chen, B. Crasemann: At. Data Nucl. Data Ta-

bles 33,217(1985)

50.39 R. Glauber: Lectures in Theoretical Physics,Vol.2

(Interscience, New York 1958)

50.40 V. Franco, B. K. Thomas: Phys. Rev. A 4,945(1971)

50.41 J. Binstock, J. F. Reading: Phys. Rev. A 11,1205

(1975)

50.42 B. H. Bransden, D. P. Dewangen: J. Phys. B 12, 1371

(1979)

50.43 G. Basbas, W. Brandt, R. H. Ritchie: Phys. Rev. A 7,

1971 (1973)

50.44 W. Brandt, G. Lapicki: Phys. Rev. A 23, 1717 (1981)

50.45 W. Fritsch, C. D. Lin: Phys. Rep. 202, 1 (1991)

50.46 T. G. Winter: Phys. Rev. 56, 2903 (1997)

50.47 C. O. Reinhold, R. E. Olson, W. Fritsch: Phys. Rev. A

41, 4837 (1990)

50.48 A. L. Ford, J. F. Reading, K. A. Hall: J. Phys. B 26,

4537, 4553 (1993)

50.49 J. F. Reading, A. L. Ford, G. L. Swafford, A. Fitchard:

Phys. Rev. A 20, 130 (1979)

50.50 R. L. Becker, A. L. Ford, J. F. Reading: J. Phys. B 13,

4059 (1980)

50.51 R. Shakeshaft: Phys. Rev. A 18, 1930 (1978)

50.52 W. Fritsch, C. D. Lin: Phys. Rev. A 27, 3361 (1983)

50.53 A. M. Ermolaev: J. Phys. B 23, L45 (1990)

50.54 H. A. Slim: J. Phys. B 26, L743 (1993)

50.55 M. J. Antal, D. G. M. Anderson, M. B. McElroy:

J. Phys. B 8, 1513 (1975)

50.56 T. G. Winter, C. D. Lin: Phys. Rev. A 29, 567 (1984)

50.57 J. F. Reading, A. L. Ford, R. L. Becker: J. Phys. B 14,

1995 (1981)

50.58 J. F. Reading, A. L. Ford, R. L. Becker: J. Phys. B 15,

625, 3257 (1982)

50.59 B. H. Choi: Phys. Rev. A 11, 2004 (1975)

50.60 A. L. Ford, E. Fitchard, J. F. Reading: Phys. Rev. A

16, 133 (1977)

50.61 G. Mehler, W. Greiner, G. Soff: J. Phys. B 20,2787

(1987)

50.62 T. Mukoyama, C. D. Lin, W. Fritsch: Phys. Rev. A 32,

2490 (1985)

50.63 E. Y. Sidky, C. D. Lin: J. Phys. B 31, 2949 (1998)

50.64 B. Pons: Phys. Rev. Lett. 84, 4569 (2000)

50.65 J. Fu, M. J. Fitzpatrick, J. F. Reading, R. Garet: J.

Phys. B 34, 15 (2001)

50.66 M. Brauner, J. S. Briggs, H. Klar: J. Phys. B 22, 2265

(1989)

50.67 J. S. Briggs: Phys. Rev. A 41, 539 (1990)

50.68 C. Dal Cappello, H. Le Rouzo: Phys. Rev. A 43,1395

(1991)

Part D 50

761

Ion–Atom Cha

51. Ion–Atom Charge Transfer Reactions

at Low Energies

Ion–atom charge exchange reactions contribute

signiﬁcantly to the ionization balance of complex

ions in many natural environments (astrophysical

photoionized plasmas such as planetary nebulae,

nova shells, etc.) [51.1]. For electron temperatures

lower than 10

K, the abundance of neutral

atomic H or He can be sufﬁcient for the charge

exchange rate to exceed the radiative (direct or

dielectronic) recombination rate for ions with

charge q ≥ 2[51.2]. In the case of singly charged

ions, accidental resonance conditions are required

for the charge exchange rate to be large at thermal

energies. In this chapter, we shall limit discussion

to the case of q ≥ 2. We may distinguish two types

of reaction: type I, for which electron capture

takes place with no change in the conﬁguration of

the core electrons, and type II, for which electron

capture is accompanied by a rearrangement of the

core electron conﬁguration.

We shall concentrate on the low energy range

(less than a few hundred eV), where an adiabatic

representation of the collision complex can

successfully describe the collision dynamics [51.3].

Nonadiabatic transitions tend to occur in the

vicinity of avoided potential energy crossings. For

the transition probability to be appreciable, the

energy separation ∆

at the crossing radius R

51.1 Molecular Structure Calculations ........... 762

51.1.1 Ab Initio Methods...................... 762

51.1.2 Model Potential Methods ........... 763

51.1.3 Empirical Estimates ................... 764

51.2 Dynamics of the Collision ..................... 765

51.3 Radial and Rotational Coupling

Matrix Elements .................................. 766

51.4 Total Electron Capture Cross Sections ..... 767

51.5 Landau–Zener Approximation............... 769

51.6 Differential Cross Sections .................... 769

51.7 Orientation Effects............................... 770

51.8 New Developments .............................. 772

References .................................................. 772

must be neither too large nor too small (0.1 <∆

3 eV). Since the size of ∆

is determined by electron

exchange, whose effect varies exponentially

with internuclear distance, only crossings in

the range 3 ≤ R

≤ 15a

induce nonadiabatic

transitions. Because of this constraint, the

number of effective curve crossings is quite small

and the electron capture process is very state

selective [51.3].

In general, electron capture is of type I for q ≥ 3 and of

type II for q = 2. In a few cases, type II processes can

also occur for q = 3.

Although there are a few direct experimental meas-

urements at eV energies [51.4], most measurements

have been carried out at collision energies exceed-

ing a few 100 eV [51.5]. Unfortunately, the processes

which dominate in the higher energy range become

negligible at eV energies (and vice versa). Most es-

timates of the cross sections in the thermal–eV range

are based on theoretical models. Since at thermal ener-

gies, orbiting and tunneling effects may be considerable,

a quantum mechanical description of the collision is

preferable.

The dynamic coupling matrix elements between

different molecular states depend on the origin of

the electronic coordinates, and the corresponding scat-

tering equations are not invariant with respect to

a Galilean transformation. In a semiclassical formu-

lation of the dynamics, this defect can be removed

by the introduction of translation factors [51.6–12].

However, in a quantum mechanical formulation, it

is more appropriate to introduce reaction coordinates

of a more ﬂexible form than those used traditionally

in the Born–Oppenheimer approximation. The most

convenient is the Eckart coordinate system [51.9],

which leads to a simple modiﬁcation of the nonadia-

batic coupling matrix elements, and which is well

Part D 51