Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics
Подождите немного. Документ загружается.


680 Part D Scattering Theory
(45.247) yields the forward glory amplitude
f
FG
=
1
k
2
n=1
∞
m=0
λ
mn
2π
|χ
m
|
1/2
× J
0
(λ
mn
θ) e
iS
(g)
mn
, (45.248)
S
(g)
mn
= 2η(λ
mn
) +mπ(λ
mn
−1) −
3
4
π.
(45.249)
Backward Glories. Contributions arising from χ =
−π ±α, −3π ±α, ···, −(2m −1)π ±α coalesce as
α ≡ π −θ → 0. The phase function near a backward
glory is
η(λ) = η(λ
m
) +
1
2
χ
m
(λ −λ
m
) +
1
4
χ
m
(λ −λ
m
)
2
.
(45.250)
The m = 0 term provides the normal backward ampli-
tude due to head-on (b = 0) repulsive collisions. m > 0
terms provide contributions from attractive collisions for
which there are two points λ
mn
of stationary phase for
each m in χ
m
=−(2m −1)π ±α.
The backward glory amplitude at θ = π −α is
f
BG
=
1
k
2
n=1
∞
m=0
λ
mn
2π
|χ
mn
|
1/2
× J
0
(λ
mn
α) e
iS
(g)
mn
, (45.251)
S
(g)
mn
= 2η(λ
mn
) +π(2m −1)
λ
mn
−
1
2
−
3
4
π.
(45.252)
In contrast to the Bessel amplitudes (below), these
transitional formulae do not uniformly connect with the
primitive semiclassical results for ( f
1
+ f
2
) away from
the critical glory angles.
Uniform Bessel Amplitude for Glory Scattering
The combined contributions from χ
1
=−Nπ +θ and
χ
2
=−Nπ −θ,whereN = 2m, for forward and N =
2m −1 for backward scattering, yield [45.9]
f
G
(θ) =
α
j
2i
e
−iNπ/2
πS
(C )
21
1/2
exp
i
¯
S
(C )
(θ)
×
(σ
1/2
1
+σ
1/2
2
)J
0
1
2
S
(C )
21
− i(σ
1/2
1
−σ
1/2
2
)J
1
1
2
S
(C )
21
,
(45.253)
where S
(C )
21
(θ) = S
(C )
2
−S
(C )
1
is the difference of the
collision actions (45.231a),
S
(C )
i
(θ) = 2η(λ
i
) −λ
i
χ
i
, i = 1, 2 , (45.254)
with mean
¯
S
(C )
21
(θ) =
1
2
S
(C )
2
+S
(C )
1
,
(45.255)
and phases
α
j
= e
±iπ/4
; (+), χ
j
> 0; (−), χ
j
< 0 ,
(45.256)
and the ordinary Bessel functions J
n
(Z) satisfy the
relationships J
1
(z) =−J
0
(z), J
1
(−z) =−J
1
(z).This
formula, valid for both forward (θ ∼ 0) and backward
(θ ∼ π) glories, does uniformly connect the primitive
result for ( f
1
+ f
2
), valid when S
(C )
21
1tothetransi-
tional results (45.248)and(45.251), valid only in the
vicinity of the glories.
45.3.6 Small-Angle (Diffraction) Scattering
Diffraction originates from scattering in the forward di-
rection by the long-range attractive tail of V(R) where
χ, χ
and η →0. The main contributions to (45.222a)
arise from a large number of small η(λ) at large λ.The
Jeffrey–Born phase function (45.173) can therefore be
used in (45.222b)for f(θ) andin(45.45)and(45.47),
respectively, for σ(E). A finite forward diffraction peak
as θ → 0 is obtained for f(θ) in contrast to the classical
infinite result.
Integral Cross Sections
For V(R) =−C/R
n
, the Landau–Lifshitz (LL)and
Massey–Mohr (MM) cross sections are [cf. (45.346)]
σ
LL
(E) = π
2CF(n)
(n −1) v
2/(n−1)
× π
sin
π
n −1
Γ
2
n −1
−1
,
(45.257)
σ
MM
(E) = π
2CF(n)
(n −1) v
2/(n−1)
2n −3
n −2
,
(45.258)
where F(n) =
√
πΓ
1
2
n +
1
2
/Γ
1
2
n
and v is the rela-
tive speed. For σ
MM
, the phases are η(λ) =
1
2
(0 <λ<
λ
0
) and η(λ) = η
JB
(λ > λ
0
).Forσ
LL
, phases are η
JB
Part D 45.3
Elastic Scattering: Classical, Quantal, and Semiclassical 45.3 Semiclassical Scattering Formulae 681
for all λ.Bothσ
LL
and σ
MM
have the general form
σ
D
(E) = γ
C
v
2/(n−1)
. (45.259)
Ion–Atom Collisions. For n =4 attraction at low energy,
σ
D
∼ v
−2/3
. γ
LL
= 11.373, γ
MM
= 10.613. For n = 12
repulsion at high energy, σ
D
∼ v
−2/11
. γ
LL
= 6.584,
γ
MM
= 6.296.
Atom–Atom Collisions. For n = 6 (attraction), σ
D
∼
v
−2/5
, γ
LL
= 8.083, γ
MM
= 7.547 Fig. 45.1.
Exact numerical calculations favor σ
LL
over σ
MM
([45.10], pp. 1325 for details).
Differential Cross Section
dσ
dΩ
= f
2
i
(θ) + f
2
r
(θ) , (45.260a)
f
i
=
2
k
∞
0
λ sin
2
η(λ)
1 −
1
4
λ
2
θ
2
dλ
(45.260b)
=
kσ
D
(E)
4π
1−
k
2
σ
D
16π
g
1
(n)θ
2
,
(45.260c)
f
r
=
1
k
∞
0
λ sin 2η(λ)
1 −
1
4
λ
2
θ
2
dλ
(45.260d)
=
kσ
D
(E)
4π
1 −
k
2
σ
D
16π
g
2
(n)θ
2
×tan
π
n −1
,
(45.260e)
where σ
D
is given by (45.259), and
g
j
(n) = π
−1
tan
jπ
n −1
{
Γ
[
2/(n −1)
]
}
2
Γ
[
4/(n −1)
]
.
(45.261)
The optical theorem (45.62) is satisfied, and
f
D
(θ ∼ 0) = σ
1/2
D
(E) e
iS
D
(n)
, (45.262)
where the (energy-independent) phase is
S
D
(n) =
π(n −3)
2(n −1)
.
(45.263)
45.3.7 Small-Angle (Glory) Scattering
Amplitude and Cross Section. The other contribution to
forward scattering is the forward glory, which originates
from the combined null effect of attraction and repul-
sion at a specified glory impact parameter b
g
= λ
g
/k,
where η(λ) attains a maximum value of η
g
.Them = 0
term of (45.248) yields
f
G
(θ) = σ
1/2
G
(θ) exp
[
iS
G
(E)
]
, (45.264a)
σ
G
(θ) =
λ
2
g
k
2
2π
|χ
g
|
J
2
0
(λ
g
θ) , (45.264b)
S
G
(E) = 2η
g
(E) −
3
4
π,
(45.264c)
where J
2
0
(x) ∼ 1 −
1
4
x
2
+···. The classical re-
sult (45.30) is recovered by averaging (45.264b) over
several oscillations with
J
2
0
(x)
= (πx)
−1
.
Diffraction-Glory Oscillations.
σ(E) =
4π
k
Im
[
f
D
(0) + f
G
(0)
]
(45.265a)
= σ
D
(E) +∆σ
G
(E), (45.265b)
where the diffraction cross section is (45.259), and
where
∆σ
G
(E) =
4π
k
2
λ
g
*
2π
|χ
g
|
+
1/2
sin
2η
g
(E) −
3
4
π
(45.266)
oscillates with E.
For sufficiently deep attractive wells, the phase
shift η
g
successively decreases with increasing E
100
10
1
0.1
0.001 0.01 0.1 1 10 100
Glory number N
Symmetry
oscillations
86421
RT
Orbiting
resonances
E
*
= 0.8
×10
~v
*
0
–2/5
~v
*
0
–2/11
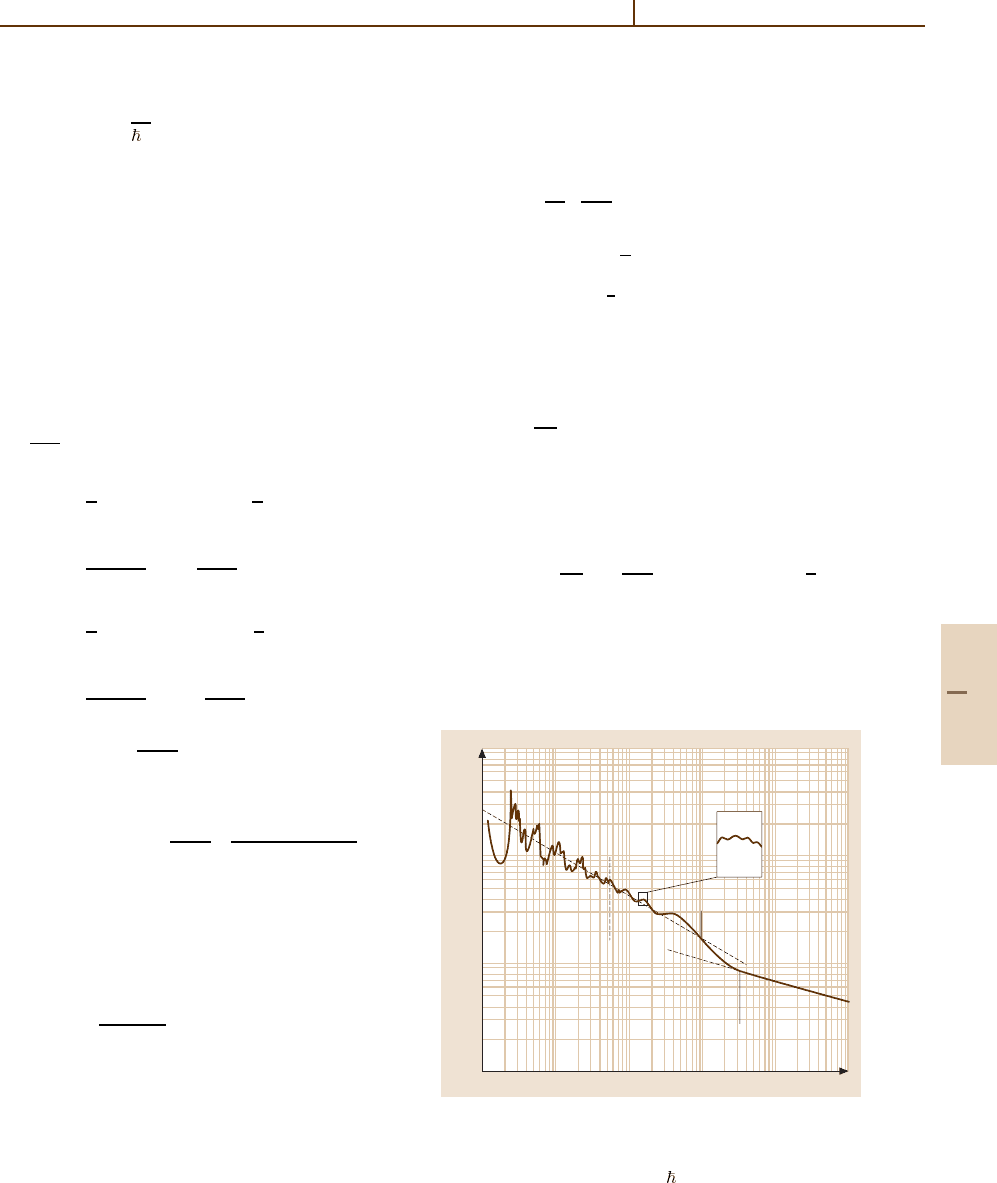
Fig. 45.1 Illustration of all the various oscillatory effects
for elastic scattering by a Lennard–Jones (12,6) poten-
tial of well depth and equilibrium distance R
e
.Ordinate
σ
∗
= σ/(2πR
2
e
), abscissa v
∗
= v/(R
e
)
Part D 45.3

682 Part D Scattering Theory
through a series of multiples of π/2. Writing
η
g
(E) = π
N −3/8
, maxima appear at N = 1, 2,...,
and minima at N = 3/2, 5/2, 7/2,.... The glories are
indexed by N in order of appearance, starting at high en-
ergies. η
g
(E → 0) is related to the number n of bound
states by Levinson’s theorem: η
0
(E →0) =
n +1/2
π.
Diffraction-glory oscillations also occur in the DCS at
a frequency governed entirely by the energy variation of
η
g
(E) and n of (45.263).
JWKB Formulae for Shape Resonances
and Tunneling Predissociation
For the three classical turning points R
1
< R
2
< R
3
at
energies E below the orbiting threshold V
max
at R
X
,the
JWKB phase shift
η
=
η
(0)
−
1
2
φ(γ
)
+η
(r)
(45.267)
is composed of (a) the phase shift
η
(0)
= lim
R→∞
∞
R
3
k(R) dR −kR +
1
2
( +
1
2
)π
(45.268)
appropriate to one turning point at R
3
, (b) a contri-
bution η
(r)
arising from the region between the two
inner turning points R
2
and R
3
due to penetration of
the centrifugal barrier and given by
tan η
(r)
(E) =
*
1 +exp(−2γ
)
1/2
−1
1 +exp(−2γ
)
1/2
+1
+
×tan
α
−
1
2
φ
,
(45.269)
and (c) a phase correction factor
φ
(γ
) = arg Γ
1
2
+i
− ln ||+,
(45.270)
where =−γ
/π. The radial action J
R
(E) is 2 α
(E).
For motion within the potential well α
is
α
(E) =
R
2
R
1
k(R) dR , (45.271)
and is
γ
(E < E
max
) =
R
3
R
2
|k(R)| dR (45.272)
in the classically forbidden region of the potential hump.
The above expressions also hold for energies E >
V
max
, except that (45.272) is replaced by
γ
(E > E
max
) =−i
R
+
R
−
k(R) dR , (45.273)
where R
±
are the complex roots of k
(R) = 0. For the
quadratic form
V(R) = V
max
−
1
2
Mω
2
∗
(R − R
max
)
2
, (45.274)
appropriate in the vicinity of the potential hump, γ for
both cases reduces to
γ = π(V
max
−E)/ ω
∗
. (45.275)
The deflection function χ
= 2(∂η
/∂) no longer
diverges at the orbiting angular momentum
0
or im-
pact parameter b
0
. The singularities in η
of (45.51)are
exactly canceled by −
1
2
(∂φ/∂) in (45.270).
Limiting cases:
(a) E V
max
.Thenγ
→−∞ and φ →
−(π/24γ
) → 0, so that η
(r)
→ α
and η
reduces to
the single turning point result (45.268) with R
3
= R
1
.
(b) E V
max
.Thenγ
1and
η
(r)
(E) = tan
−1
1
2
e
−2γ
tan
α
−
1
2
φ
,
(45.276)
which remains negligible except for those energies E
close to quasibound energy levels E
n
determined via
the Bohr quantization condition
α
(E) −
1
2
φ
(E) =
n +
1
2
π.
(45.277)
As E increases past each E
n
, η
(r)
increases rapidly
by π.Since(∂J/∂E)
n
=ν
−1
n
=2π/ω
n
, the time period
for radial oscillation within the potential barrier, the level
spacing is
ω
n
= hν
n
= π(∂E/∂α)
n
.
Shape Resonance. In the neighborhood of E
n
∼ E,
α
(E) = α
n
(E
n
) +
π
ω
n
(E − E
n
),
(45.278)
and, under the assumption that the energy variation of φ
can be neglected, (valid for E not close to V
max
), then
η
reduces to the Breit–Wigner form
η
(E) = η
(0)
(E) +tan
−1
Γ
n
/2
E
n
−E
,
(45.279)
Part D 45.3
Elastic Scattering: Classical, Quantal, and Semiclassical 45.4 Elastic Scattering in Reactive Systems 683
with resonance width
Γ
n
= 2
ω
n
π
1 +exp(−2γ
n
)
1/2
−1
1 +exp(−2γ
n
)
1/2
+1
,
(45.280)
where γ
n
= γ(E
n
). The partial cross sections are
then determined by (45.166a,b) with η
(0)
replaced by
η
(0)
−
1
2
φ(γ) of (45.268).
Gamow’s Result. For E V
max
, γ
n
1, then
Γ
n
γ 1
−→
ω
n
2π
exp(−2γ
n
). (45.281)
The probabilities of transmission through and re-
flection from a barrier for unit incident flux from the left
are:
Transmission Probability:
T =
1 + e
2γ
−1
γ 1
−→ e
−2γ
. (45.282)
Reflection Probability:
R =
1 + e
−2γ
−1
γ 1
−→ 1 . (45.283)
Frequency of leakage:
ν
T
= Γ
n
/ =
ω
n
2π
e
−2γ
. (45.284)
45.3.8 Oscillations in Elastic Scattering
Figure 45.1 is an illustration [45.11] of all the various
oscillatory structure and effects – Ramsauer–Townsend
minimum (Sect. 45.2.4), orbiting resonances (45.340),
diffraction-glory oscillations (45.265b) and symmetry
oscillations (45.82) – for elastic scattering by a Lennard–
Jones (12, 6) potential. Note the shift of velocity
dependence from v
−2/5
at low v to v
−2/11
at high v.
σ =2πR
2
e
is the averaged cross section 2πb
2
0
in (45.47)
at b
0
= R
e
. The region σ
∗
> 1 probes the attractive
part of the potential at low speeds and σ
∗
< 1 probes
the repulsive part at high speeds. The four distinct
types of structure originate from nonrandom behav-
ior of sin
2
η in (45.45). Orbiting trajectories exist for
E < 0.8 (Sect. 45.5).
45.4 Elastic Scattering in Reactive Systems
All nonelastic processes (e.g. inelastic scattering and
rearrangement collisions/chemical reactions) can be
viewed as a net absorption from the incident beam
current vector J and modeled by a complex optical
potential
V(R) = V
r
(R) +iV
i
(R). (45.285)
The continuity equation is then
∇· J =−
2
V
i
(R)|Ψ(R)|
2
, (45.286)
so that particle absorption implies V
i
> 0 and particle
creation V
i
< 0. Since particle conservation implies
|S
|
2
= 1, the phase shift
δ
(k) = η
(k) +iγ
(k) (45.287)
is also complex since then
S
= A
(k) exp(2iη
), (45.288)
where the absorption (inelasticity) factor is
A
= exp(−2γ
) ≤ 1 . (45.289)
45.4.1 Quantal Elastic, Absorption
and Total Cross Sections
f
el
(θ) =
1
2ik
∞
=0
(2 +1)
A
e
2iη
−1
P
(cos θ) ,
(45.290a)
σ
el
(k) =
π
k
2
∞
=0
(2 +1)|A
e
2iη
−1|
2
, (45.290b)
σ
abs
(k) =
π
k
2
∞
=0
(2 +1)
1 − A
2
,
(45.290c)
σ
tot
(k) = σ
el
(k) +σ
abs
(k)
=
2π
k
2
∞
=0
(2 +1)
(
1 − A
cos 2η
)
.
(45.290d)
Upper limits to the partial cross sections are
σ
el
≤
4π
k
2
(2 +1), σ
abs
≤
π
k
2
(2 +1),
(45.291a)
Part D 45.4

684 Part D Scattering Theory
σ
tot
≤
4π
k
2
(2 +1) =
4π
k
Im
f
el
(θ = 0)
.
(45.291b)
For pure elastic scattering with no absorption, A
= 1.
All nonelastic processes (0 ≤ A
< 1) are always ac-
companied by elastic scattering, even in the (A
= 0)
limit of full absorption.
Eikonal Formulae for Forward Reactive Scattering.
f
el
(θ) =−ik
∞
0
e
2iδ
−1
J
0
(2kb sin
1
2
θ)b db ,
(45.292a)
σ
el
(k) = 2π
∞
0
|
1 − e
−2γ
e
2iη
|
2
b db , (45.292b)
σ
abs
(k) = 2π
∞
0
1 −e
−4γ
b db ,
(45.292c)
σ
tot
(k) = 4π
∞
0
1 − e
−2γ
cos 2η
b db , (45.292d)
where the phase shift function δ = η +iγ at impact
parameter b can be either the Jeffrey–Born phase
δ
JB
(b) =−
1
2k
∞
b
U(R) dR
1 −b
2
/R
2
1/2
, (45.293)
where kb = λ = ( +1/2), or the eikonal phase
δ
E
(b) =−
1
4k
∞
−∞
U(b, Z) dZ , (45.294)
where the reduced interaction is U =
2m/
2
V .
Fraunhofer Diffraction by a Black Sphere. For a com-
plex spherical well U
U =
#
U
r
+iU
i
, R < a
0, R > a .
(45.295)
The eikonal phase function (45.294)is
δ(b) =
#
(U/2k)
a
2
−b
2
1/2
, 0 ≤b ≤ a
0 b > a .
(45.296)
The absorption factor is
A(b)
2
≡ e
−4γ
= exp
−2
a
2
−b
2
1/2
/λ
,
(45.297)
where λ = k/U
i
is the mean free path towards absorp-
tion. For strong absorption, λ a,sothat
f
el
(θ) = ik
a
0
J
0
(2kb sin
1
2
θ)b db ,
(45.298)
dσ
el
dΩ
= (ka)
2
J
1
2ka sin
1
2
θ
2ka sin
1
2
θ
2
a
2
, (45.299)
which has a diffraction shaped peak of width
∼θ ≤ (ka)
−1
about the forward direction, and
σ
tot
=
4π
k
Im
f
el
(θ = 0)
= 2πa
2
(45.300)
is composed of πa
2
for classical absorption and πa
2
for edge diffraction or shadow (nonclassical) elastic
scattering. This result also holds for the perfectly re-
flecting sphere (πa
2
for classical elastic and πa
2
for
edge diffraction).
45.5 Results for Model Potentials
Exact results for various quantities in classical, quantal,
and semiclassical elastic scattering are obtained for the
model potentials (a)–(s) in Table 45.1.
Classical Deflection Functions
for Model Potentials
(a) Hard Sphere.
θ(b; E) = χ =
#
π −2sin
−1
b/a, b ≤ a ;
0, b > a .
(45.301)
b(θ) = a cos
1
2
θ,
(45.302)
σ(θ) =
dσ
dΩ
=
1
4
a
2
; isotropic, (45.303)
σ = πa
2
= geometric cross section; (45.304)
θ, σ(θ) and σ are all independent of energy E.
(b) Potential Barrier. For E < V
0
, classical scatter-
ing is the same as for hard sphere reflection as given
by (45.301–45.304). For E > V
0
and θ = χ,define
Part D 45.5
Elastic Scattering: Classical, Quantal, and Semiclassical 45.5 Results for Model Potentials 685
n
2
= 1 −V
0
/E, b
0
= na.Then
θ(b) =
#
2
sin
−1
(b/na) −sin
−1
(b/a)
0 ≤ b ≤ b
0
π −2sin
−1
(b/a), b
0
≤ b ≤ a
(45.305)
and θ
max
= 2cos
−1
n.Foragivenθ, the two impact
parameters which contribute are
b
1
(θ) =
an sin
1
2
θ
1 −2n cos
1
2
θ +n
2
1/2
, 0 < b
1
≤ b
0
(45.306)
b
2
(θ) = a cos
1
2
θ, b
0
< b
2
≤ a
(45.307)
Table 45.1 Model interaction potentials
Potential V(R)
(a) Hard sphere ∞, R ≤ a; 0, R > a
(b) Barrier V
0
, R ≤ a; 0, R > a
(c) Well −V
0
, R ≤ a; 0, R > a
(d) Coulomb (±) ±k/R
(e) Finite-range Coulomb −k/R +k/R
s
R ≤ R
s
; 0, R > R
s
(f) Pure dipole ±α/R
2
(g) Finite-range dipole ±α
1
R
2
−
1
a
2
, R ≤ a; 0, R > a
(h) Dipole + hard sphere ±α/R
2
, R ≤ a; 0, R > a
(i) Power law attractive −C/R
n
,(n > 2)
(j) Fixed dipole + polarization −
De cos θ
d
R
2
−
α
d
e
2
2R
4
(k) Fixed dipole + Coulomb −
De cos θ
d
R
2
+
e
2
R
(l) Lennard- Jones (n, 6)
n
n −6
'
6
n
R
e
R
n
−
R
e
R
6
"
(m) Polarization (n, 4)
n
n −4
'
4
n
R
e
R
n
−
R
e
R
4
"
(n) Multiple-term power law
C
m
R
m
−
C
n
R
n
= V
m
(R) −V
n
(R)
(o) Exponential V
0
exp(−αR )
(p) Screened Coulomb V
0
exp(−αR )/ R
(q) Morse
e
2β(R
e
−R)
−2e
β(R
e
−R)
(r) Gaussian V
0
exp(−α
2
R
2
)
(s) Polarization finite −V
0
/(R
2
+ R
2
0
)
2
For 0 ≤ θ ≤θ
max
,
dσ
dΩ
=
1
4
a
2
+
a
2
n
2
n cos
1
2
θ −1
n −cos
1
2
θ
4cos
1
2
θ
1 +n
2
−2cos
1
2
θ
,
(45.308)
and dσ/dΩ = 0forθ
max
≤ θ ≤ π. Finally,
σ =
θ
max
θ=0
dσ
dΩ
dΩ = πa
2
. (45.309)
(c) Potential Well. Results are similar to the potential
barrier case above, except that there is only a single scat-
tering trajectory with θ =−χ,andn =(1 +V
0
/E)
1/2
is
the effective index of refraction for the equivalent prob-
lem in geometrical optics. Refraction occurs on entering
Part D 45.5
686 Part D Scattering Theory
and exiting the well. Then
θ(b) =−2
sin
−1
(b/na) −sin
−1
(b/a)
,
(45.310)
θ(b = a) = θ
max
= 2cos
−1
(1/n), (45.311)
b(θ) =
−an sin
1
2
θ
1 −2n cos
1
2
θ +n
2
1/2
, (45.312)
dσ
dΩ
=
a
2
n
2
n cos
1
2
θ −1
n −cos
1
2
θ
4cos
1
2
θ
n
2
+1 −2n cos
1
2
θ
2
,
(45.313)
σ = πa
2
(45.314)
(d) Rutherford or Coulomb.
θ(b, E) =|χ|=2csc
−1
1 +(2bE/k)
2
1/2
,
(45.315)
b(θ, E) = (k/2E) cot
1
2
θ,
(45.316)
σ(θ) =
dσ
dΩ
=
k
4E
2
csc
4
1
2
θ.
(45.317)
(e) Finite Range Coulomb.
R
0
(E) =
k
2E
,α(E) = R
0
(E)/R
s
,
dσ
dΩ
=
R
2
0
4
*
1 +α
α
2
+(1 +2α) sin
2
1
2
θ
+
2
. (45.318)
(f) Pure Dipole. R
2
0
(E) = α/E.
Repulsion (+): χ>0, χ = θ ,
b
2
(χ) = R
2
0
1
χ
+
1
2π −χ
π
2
−1
,
(45.319)
dσ
dΩ
=
πR
2
0
4sinθ
|
1
θ
2
−
1
(2π −θ)
2
| . (45.320)
Attraction (−): χ<0.
b
2
(χ) = R
2
0
1
|χ|
−
1
|χ|+2π
π
2
+1
.
(45.321)
There is an infinite number of (negative) deflections χ =
χ
±
n
associated with a given scattering angle θ:
|χ
+
n
|=2πn +θ, n = 0, 1, 2,... , (45.322a)
|χ
−
n
|=2πn −θ, n = 1, 2, 3,... . (45.322b)
The infinite sum over contributions from b
±
n
= b(χ
±
n
)
for the attractive dipole yields
dσ
dΩ
=
πR
2
0
4sinθ
1
θ
2
+
1
(2π −θ)
2
.
(45.323)
(g) Finite Range Dipole Scattering. R
2
0
= α/E,
R
±
c
2
= b
2
± R
2
0
,
b
±
0
2
= a
2
± R
2
0
.
Repulsion (+): for b ≤a,
χ(b) =
π
R
+
c
−b
R
+
c
+
2b
R
+
c
sin
−1
*
R
+
c
b
+
0
+
−2sin
−1
b
a
,
(45.324)
χ(0) = π, χ(b ≥ a) = 0 ,σ= πa
2
.
Attraction (−): for b > R
0
,
χ(b) =
π
R
−
c
−b
R
−
c
+
2b
R
−
c
sin
−1
*
R
−
c
b
−
0
+
−2sin
−1
b
a
,
(45.325)
χ(R
0
) →∞,χ(b ≥ a) = 0 ,σ= πa
2
.
(h) Dipole + Hard Sphere Scattering. R
2
0
= α/E,
(R
±
c
)
2
= b
2
± R
2
0
, (b
±
0
)
2
= a
2
± R
2
0
.
Repulsion (+): for 0 ≤ b ≤ b
0
,
χ(b) =
π
R
+
c
−b
R
+
c
+
2b
R
+
c
sin
−1
R
+
c
a
−2sin
−1
b
a
,
(45.326)
b
0
≤ b ≤ a; χ(b) = π −2sin
−1
(b/a),
(45.327)
χ(0) = π, χ(b ≥ a) = 0 ,σ= πa
2
.
(45.328)
Attraction (−): for b > R
0
,
χ(b) =
π(R
−
c
−b)
R
−
c
+
2b
R
−
c
sin
−1
R
−
c
a
−2sin
−1
b
a
,
(45.329)
χ(b) = χ
min
at b = a ,
χ(0) = π, χ(b ≥ a) = 0 ,σ= πa
2
.
Part D 45.5
Elastic Scattering: Classical, Quantal, and Semiclassical 45.5 Results for Model Potentials 687
Orbiting or Spiraling Collisions
From Sect. 45.1.7, the parameters are
Orbiting radius: R
0
.
Focusing factor: F =
[
1 −V(R
0
)/E
]
.
Orbiting cross section: σ
orb
= πR
2
0
F.
(i) Attractive Power Law Potentials.
V
eff
(R
0
) = (1 −
1
2
n)V(R
0
), n > 2,
R
0
(E) =
(n −2)C
2E
1/n
, F =
n
(n −2)
,
(45.330)
σ
orb
(E) = π
n
(n −2)
(n −2)C
2E
2/n
.
(45.331)
For the case n = 4 with V(R) =−α
d
e
2
/2R
4
,this
gives the Langevin cross section
σ
L
(E) = 2πR
2
0
= 2π
α
d
e
2
2E
1/2
(45.332)
for orbiting collisions, and the Langevin rate
k
L
= vσ
L
(E) = 2π
α
d
e
2
/M
1/2
, (45.333)
which is independent of E.
The case n = 6 with V(R) =−C/R
6
is the van der
Waals potential for which
σ
orb
(E) =
3
2
πR
2
0
=
3
2
π
(
2C/E
)
1/3
. (45.334)
(j) Fixed Dipole plus Polarization Potential.
R
2
0
(E) =
α
d
e
2
2E
1/2
, (45.335)
σ
orb
(E) = 2π
α
d
e
2
2E
1/2
+
πDe cos θ
d
E
.
(45.336)
For a locked-in dipole, the orientation angle is θ
d
= 0,
and σ
orb
(E)>0forallθ
d
when E > E
c
= (D
2
/2α
d
).
On averaging over all θ
d
from 0 to θ
max
=
1
2
π +
sin
−1
2ER
2
0
/De
, which satisfies σ
orb
(E)>0forall
E,then
σ
orb
(E)
θ
d
= π
'
α
d
e
2
2E
1/2
+
α
d
e
2
2E
c
1/2
"
+
πDe
4E
1 −
E
E
c
(45.337a)
→ σ
L
(E)asE → E
c
. (45.337b)
(k) Fixed Dipole + Coulomb Repulsion.
R
2
0
(E) = e
2
/2E . (45.338)
For all E and fixed rotations in the range 0 ≤θ
d
≤θ
max
=
cos
−1
e
2
/2De
,
σ
orb
(E) = (πDe cos θ
d
)/E −πR
2
0
(E). (45.339)
(l) Lennard–Jones (n‚6). For the following two inter-
actions, there are two roots of E = V
eff
(R
0
) = V(R
0
) +
1
2
R
0
V
(R
0
). They correspond to stable and unstable cir-
cular orbits [with different angular momenta associated
with the minimum and maxima of the different V
eff
(R)].
Analytical expressions can only be derived for the orbit-
ing cross section at the critical energy E
max
above which
no orbiting can occur.
For the Lennard–Jones (n, 6) potential, orbiting oc-
curs for E < E
max
= 2[4/(n −2)]
6/(n−6)
. The orbiting
radius at E
max
is
R
0
(E
max
) = R
e
[
(n −2)/4
]
1/(n−6)
.
The orbiting cross section at E
max
= 2(R
e
/R
0
)
6
is
σ
orb
(E
max
) = πb
2
0
(E
max
) =
3
2
πR
2
0
n
n −2
.
(45.340)
n = 12 : E
max
= 4/5 , R
0
= 1.165R
e
,
σ
orb
= 2.4πR
2
e
.
(m) Polarization (n‚4). As discussed for case (l),
E
max
=
2
n −2
4/(n−4)
, (45.341)
R
0
(E
max
) = R
e
n −2
2
1/(n−4)
, (45.342)
σ
orb
(E
max
) = 2πR
2
0
n
(n −2)
,
(45.343)
n = 12 : E
max
= /
√
5 ;
R
0
= 1.22R
e
;σ
orb
= 3.6πR
2
e
.
Small-Angle Scattering
For the power law potential V(R) =−C/R
n
,(45.12) can
be expanded in powers of V(R)/E to obtain analytic
expressions for χ and η
JB
. The general form is
χ(b) =
∞
j=1
V(b)
E
j
F
j
(n) =
2
k
∂η
∂b
,
(45.344)
F
j
(n) =
π
1/2
Γ
1
2
jn +
1
2
Γ( j +1)Γ
1
2
jn − j +1
.
(45.345)
Part D 45.5
688 Part D Scattering Theory
The leading j = 1 terms equivalent to (45.16b)are
F
1
(n) ≡ F(n), as defined following (45.257). Then to
first order in V/E,
η
JB
=−
k
2E
CF(n)
n −1
b
1−n
, (45.346)
dσ
dΩ
= I
c
(θ) =
CF(n)
Eθ
2/n
1
nθ sin θ
.
(45.347)
From a log–log plot of sin θ(dσ/dΩ) versus E, C and n
can both be determined.
The integral cross sections for scattering by θ ≥ θ
0
is
σ(E) = 2π
π
θ
0
I
c
(θ) d(cos θ) = 2π
b
max
0
b db
= π
CF(n)
Eθ
0
2/n
, (45.348)
where θ
0
is the smallest measured scattering angle
corresponding to a trajectory with impact parameter,
b
max
=
[
CF(n)/Eθ
0
]
1/n
. A plot of ln σ(E) versus ln E
is a straight line with slope (−2/n).
The Landau–Lifshitz cross section (45.257)andthe
Massey–Mohr cross section (45.258) follow from use of
the JB phases (45.346).
The diffusion cross section in the Random Phase
Approximation (45.49)is
σ
d
(E) = 4π
b
c
0
sin
2
θ/2
b db , |χ(b
c
)|=
2
π
= π(C/2E)
2/n
[
πF(n)
]
2/n
. (45.349)
(n) Multiple-Term Power-Law Potentials.
χ(E, b) =
1
E
[
V
m
(b)F(m) −V
n
(b)F(n)
]
. (45.350)
For example a Lennard–Jones (n, 6) potential Table 45.1
has the following features:
Forward Glory: χ =0whenb
g
= α
1/(n−6)
n
R
e
,
where α
n
= 6F(n)/
[
nF(6)
]
.
Rainbow: dχ/ db = 0atb
r
= (nα
n
/6)
1/(n−6)
R
e
.
χ
r
=−F(n)(E /E)(R
e
/b
r
)
n
, (45.351)
ω
r
=
1
2
d
2
χ
r
/db
2
r
=
3n
b
2
r
χ(b
r
)
. (45.352)
(o) Exponential Potential.
η
JB
(E, b) =−
1
2
kb
V
0
E
K
1
(αb)R →∞
−→
−
1
2
kb
V(b)
E
πb
2α
1/2
.
(p) Screened Coulomb Potential.
χ(E, b) = α
(
V
0
/E
)
K
1
(αb)
large b
−→
1
2
παb
1/2
V(b)/E , (45.353)
η
JB
(E, b) =−
k
2E
V
0
K
0
(αb)
large b
−→ −
k
2E
V(b)
πb
2α
1/2
. (45.354)
(q) Morse Potential.
χ(E, b) = (2βb)
E
e
2βR
e
K
0
(2βb)
−e
βR
e
K
0
(βb)
large b
−→ (πβb)
1/2
E
e
2β(R
e
−b)
−
√
2e
β(R
e
−b)
,
b
r
= R
e
+(2β)
−1
ln 2 ,
χ
r
=−(πβb
r
)
1/2
(/2E),
ω
r
=β
2
|χ
r
|R
2
e
.
Large-Angle Scattering
For power law potentials V(R) = C/R
n
,
χ(b) = π −
n
j=1
E
V(b)
(2 j−1)/n
G
j
(n),
(45.355)
G
j
(n) =
(−1)
j−1
Γ( j)Γ(k)
2π
1/2
n
Γ
2 j −1
n
,
(45.356)
with k =
[
(2 j −1)/n
]
− j −
1
2
.Forthe j = 1term,
χ(b) = π −
E
C
1/n
G
1
(n)b , (45.357)
I
c
(θ) =
dσ
dΩ
=
C
E
2/n
G
−2
1
(n), (45.358)
which is isotropic. Including both j = 1and2terms
provides a good approximation to the entire repulsive
Part D 45.5

Elastic Scattering: Classical, Quantal, and Semiclassical References 689
branch of the deflection function χ.Series(45.355)
for large angles and (45.344) for small angles even-
tually diverge for impact parameters b < b
c
and b > b
c
,
respectively, where
b
c
= n
1/2
C
2E
1/n
|n −2|
1/n
|n −2|
1/2
. (45.359)
45.5.1 Born Amplitudes and Cross Sections
for Model Potentials
k
2
= 2ME/
2
, K = 2k sin
1
2
θ,
U
0
= 2MV
0
/
2
, U
0
/k
2
= V
0
/E .
(a) Exponential. V(R) = V
0
exp(−αR)
f
B
(θ) =−
2αU
0
α
2
+K
2
2
, (45.360)
σ
B
(E) =
16
3
πU
2
0
3α
4
+12α
2
k
2
+16k
4
α
4
(α
2
+4k
2
)
3
,
E→∞
−→
4
3
π
V
0
E
U
0
α
4
.
(45.361)
(b) Gaussian. V(R) = V
0
exp
−α
2
R
2
f
B
(θ) =−
π
1/2
U
0
4α
2
exp
−K
2
/4α
2
,
(45.362)
σ
B
(E) =
π
2
U
0
8α
4
V
0
E
1 −exp
−2k
2
/α
2
.
(45.363)
(c) Spherical Well. V(R) = V
0
for R < a , V(R) = 0for
R > a
f
B
(θ) =−
U
0
K
3
(
sin Ka − Ka cos Ka
)
,
(45.364)
σ
B
(E) =
π
2
V
0
E
(U
0
a
4
)
1 −(ka)
−2
+(ka)
−3
sin 2ka
− (ka)
−4
sin
2
2ka
. (45.365)
(d) Screened Coulomb. V(R) = V
0
exp(−αR)/R, V
0
=
Ze
2
, U
0
= 2Z/a
0
f
B
(θ) =−
U
0
α
2
+K
2
, (45.366)
σ
B
(E) =
4πU
2
0
α
2
α
2
+4k
2
→ π
V
0
E
U
0
α
2
.
(45.367)
When α → 0, then f
B
(θ) =−U
0
/K
2
.
(e) e
−
–Atom.
V(R) =−Ne
2
[
Z/a
0
+1/R
]
exp(−2ZR/a
0
),
(45.368)
H(1s):N= 1, Z= 1; He
1s
2
:N= 2; Z= 27/16.
f
B
(θ) =
2N
a
0
*
2α
2
+K
2
α
2
+K
2
2
+
,α=2Z/a
0
,
(45.369)
σ
B
(E) =
πa
2
0
N
2
12Z
4
+18Z
2
k
2
a
2
0
+7k
4
a
4
0
3Z
2
Z
2
+k
2
a
2
0
3
.
(45.370)
Also, f
B
decomposes (45.187)as
f
B
(K) = f
eZ
B
(K) + f
ee
B
(K)F(K), (45.371)
where f
ij
B
are two-body Coulomb amplitudes for (i, j)
scattering, and where
F(K) =
|Ψ
0
(R)|
2
exp
(
iK · R
)
dR (45.372)
is the elastic form factor.
(f) Dipole. V(R) = V
0
/R
2
.
f
B
(θ) = πU
0
/2K . (45.373)
(g) Polarization potential. V(R) = V
0
/
R
2
+ R
2
0
2
f
B
(θ) =−
1
4
π
U
0
R
0
exp(−KR
0
), (45.374)
σ
B
(E) =
*
π
3
U
0
32R
4
0
+
V
0
E
[
1 −(1
+4kR
0
) exp(−4kR
0
)
. (45.375)
References
45.1 T. F. O’Malley, L. Spruch, L. Rosenberg: J. Math.
Phys. 2, 491 (1961)
45.2 T. F. O’Malley: Phys. Rev. 130, 1020 (1962)
45.3 L. M. Biberman, G. E. Norman: Soviet Phys. (JETP)
18, 1353 (1964)
45.4 O. Hinckelmann, L. Spruch: Phys. Rev. A 3,642(1971)
Part D 45
