Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics
Подождите немного. Документ загружается.


Orientation and Alignment in Atomic and Molecular Collisions 46.2 Collisions Involving Spin-Polarized Beams 701
natural coordinate system enables disentangling of
the scattering amplitudes and generalization of the
parametrization of the density matrix for the case of
unpolarized beams in a straightforward way [46.7, 18].
The nonvanishing amplitudes f
n
(M
f
, m
f
, m
i
) in the
natural frame (Fig. 46.7)foraJ = 0 → J = 1 transition
are
f
n
1,
1
2
,
1
2
≡ f
↑
+1
= α
+
e
iφ
+
, (46.72)
f
n
1, −
1
2
, −
1
2
≡ f
↓
+1
= β
+
e
iψ
+
, (46.73)
f
n
−1,
1
2
,
1
2
≡ f
↑
−1
= α
iφ
−
−e
, (46.74)
f
n
−1, −
1
2
, −
1
2
≡ f
↓
−1
= β
−
e
iψ
−
, (46.75)
f
n
0,
1
2
, −
1
2
≡ f
↓
0
= β
0
e
iψ
0
, (46.76)
f
n
0, −
1
2
,
1
2
≡ f
↑
0
= α
iφ
0
0e
, (46.77)
where we have omitted J
i
= M
i
= 0andJ
f
= 1. Equa-
tions (46.72–46.75) represent noflip amplitudes that
leave the projectile spin unchanged while (46.76)and
(46.77) describe the cases where the electron spin is
flipped.
We first assume a polarization perpendicular to the
scattering plane, i. e., along the z-direction. In (46.44),
the density matrix for heavy atoms such as Xe or Hg
was decomposed into a pair of matrices with one having
positive reflection symmetry with respect to the scatter-
ing plane and the other one having negative reflection
symmetry, respectively. The extension of this decompos-
ition to the case of polarized electron beams is a pair of
density matrices, one for spin-up electron impact ex-
citation and one for spin-down excitation where “up”
and “down” correspond to the initial spin compo-
nent orientation with respect to the scattering plane.
Hence,
ρ
u
= σ
u
(1 −h)
1
2
1 +L
+
⊥
0 −P
+
l
e
−2iγ
00 0
−P
+
l
e
2iγ
01−L
+
⊥
+h
000
010
000
= w
↑
ρ
↑
+w
↓
ρ
↓
= w
↑
σ
u
1 −h
↑
1
2
×
1 +L
+↑
⊥
0 −P
+↑
l
e
−2iγ
↑
00 0
−P
+↑
l
e
2iγ
↑
01−L
+↑
⊥
+h
↑
000
010
000
+w
↓
σ
u
1 −h
↓
1
2
×
1 +L
+↓
⊥
0 −P
+↓
l
e
−2iγ
↓
00 0
−P
+↓
l
e
2iγ
↓
01−L
+↓
⊥
+h
↓
000
010
000
.
(46.78)
Here we have defined
L
+↑
⊥
=
α
2
+
−α
2
−
α
2
+
+α
2
−
=−P
↑
3
, (46.79)
L
+↓
⊥
=
β
2
+
−β
2
−
β
2
+
+β
2
−
=−P
↓
3
, (46.80)
P
+↑
l
e
2iγ
↑
= P
↑
1
+iP
↑
2
=−
2α
+
α
−
e
i(φ
−
−φ
+
)
α
2
+
+α
2
−
,
(46.81)
P
+↓
l
e
2iγ
↓
= P
↓
1
+iP
↓
2
=−
2β
+
β
−
e
i(ψ
−
−ψ
+
)
β
2
+
+β
2
−
,
(46.82)
σ
↑
= α
2
+
+α
2
−
+α
2
0
, (46.83)
σ
↓
= β
2
+
+β
2
−
+β
2
0
, (46.84)
σ
u
=
1
2
α
2
+
+α
2
−
+α
2
0
+β
2
+
+β
2
−
+β
2
0
=
1
2
σ
↑
+σ
↓
,
(46.85)
h
↑
= α
2
0
/σ
↑
, (46.86)
h
↓
= β
2
0
/σ
↓
, (46.87)
w
↑
= σ
↑
/(2 σ
u
), (46.88)
w
↓
= σ
↓
/(2 σ
u
) = 1 −w
↑
. (46.89)
Part D 46.2
702 Part D Scattering Theory
From these definitions it follows that
(1 −h) L
+
⊥
= w
↑
1 −h
↑
L
+↑
⊥
+ w
↓
1 −h
↓
L
+↓
⊥
, (46.90)
(1 −h) P
+
l
e
2iγ
= w
↑
1 −h
↑
P
+↑
l
e
2iγ
↑
+ w
↓
1 −h
↓
P
+↓
l
e
2iγ
↓
,
(46.91)
h = w
↑
h
↑
+w
↓
h
↓
=
α
2
0
+β
2
0
/(2σ
u
), (46.92)
P
+↑
l
2
+L
+↑
⊥
2
= P
+↑
l
2
+ P
↑
3
2
= 1 , (46.93)
P
+↓
l
2
+L
+↓
⊥
2
= P
+↓
l
2
+ P
↓
3
2
= 1 . (46.94)
Extraction of these parameters is facilitated by intro-
duction of “generalized Stoke parameters” [46.18]. In
this way, L
+↑
⊥
, L
+↓
⊥
,γ
↑
,γ
↓
may be determined. If, in
addition, h is known, e.g., by polarization analysis in
the y-direction, the following set of seven dimension-
less independent parameters can be derived from the
generalized Stokes parameters in the z-direction:
L
+↑
⊥
, L
+↓
⊥
, h
↑
, h
↓
,w
↑
;γ
↑
,γ
↓
. (46.95)
This leaves three relative phases unknown. In the nota-
tion of Fig. 46.7, we see from inspection that
∆
+
−∆
−
= δ
↑
−δ
↓
= 2
γ
↓
−γ
↑
,
(46.96)
in analogy to (46.67). A convenient choice for the
remaining phase angles is
∆
+
,∆
0
,δ
↑↓
, with
δ
↑↓
≡ φ
+
−ψ
0
. (46.97)
A complete set of dimensionless independent param-
eters is then given by
(w
↑
, L
+↑
⊥
, L
+↓
⊥
, h
↑
, h
↓
,γ
↑
,γ
↓
,∆
+
,∆
0
,δ
↑↓
).
(46.98)
Information about the remaining three phase angles
may be obtained in experiments with in-plane spin
polarization. Further analysis shows that the general-
ized Stokes parameters in the y (or x) direction with
in-plane spin polarization P
y
or P
x
provides two addi-
tional phases. None of the relative phases ∆
+
between
f
↑
+1
and f
↓
+1
, etc. enter. Determination of the final re-
maining angle requires determination of generalized
STU parameters, describing the electron spin in the exit
channel.
Table 46.2 summarizes the various cases with polar-
ized beams discussed in this section.
Table 46.2 Summary of cases of increasing complexity
for spin-polarized beams. The number of independent di-
mensionless parameters N
p
is listed, along with N
OA
,the
number determined from orientation and alignment only.
N
d
is the number of observation directions required
Variable Sect.46.2.1 Sect.46.2.2 Sect.46.2.3
Forces Coulomb +exchange +spin–orbit
Representation wave func. ρ
t,s
mn
ρ
↑,↓
mn
Refl. symmetry + + +, −
N
p
2 6 10
N
OA
2 5 9
N
d
1 1 2
46.3 Example
46.3.1 The First Born Approximation
As a simple, illustrative example, consider the predic-
tions of the first Born approximation (FBA). Here, S →P
excitation by electron impact is described as creation of
a pure p-orbital along the direction of the linear momen-
tum transfer ∆k = k
in
−k
out
, along which there is axial
symmetry. Evidently
L
FBA
⊥
= 0 , (46.99)
and consequently
P
FBA
l
= 1 . (46.100)
The alignment angle is found from simple geometri-
cal considerations, see Fig. 46.8. Denoting the incident
energy by E and the energy loss by ∆E,there-
lation between the projectile scattering angle Θ
col
and the alignment angle γ is directly read from the
k
out
⬃(E–∆E)
1/2
k
in
⬃ E
1/2
∆k
γ
FBA
Θ
col
Fig. 46.8 Diagram for evaluation of the alignment angle γ
in the first Born approximation
Part D 46.3
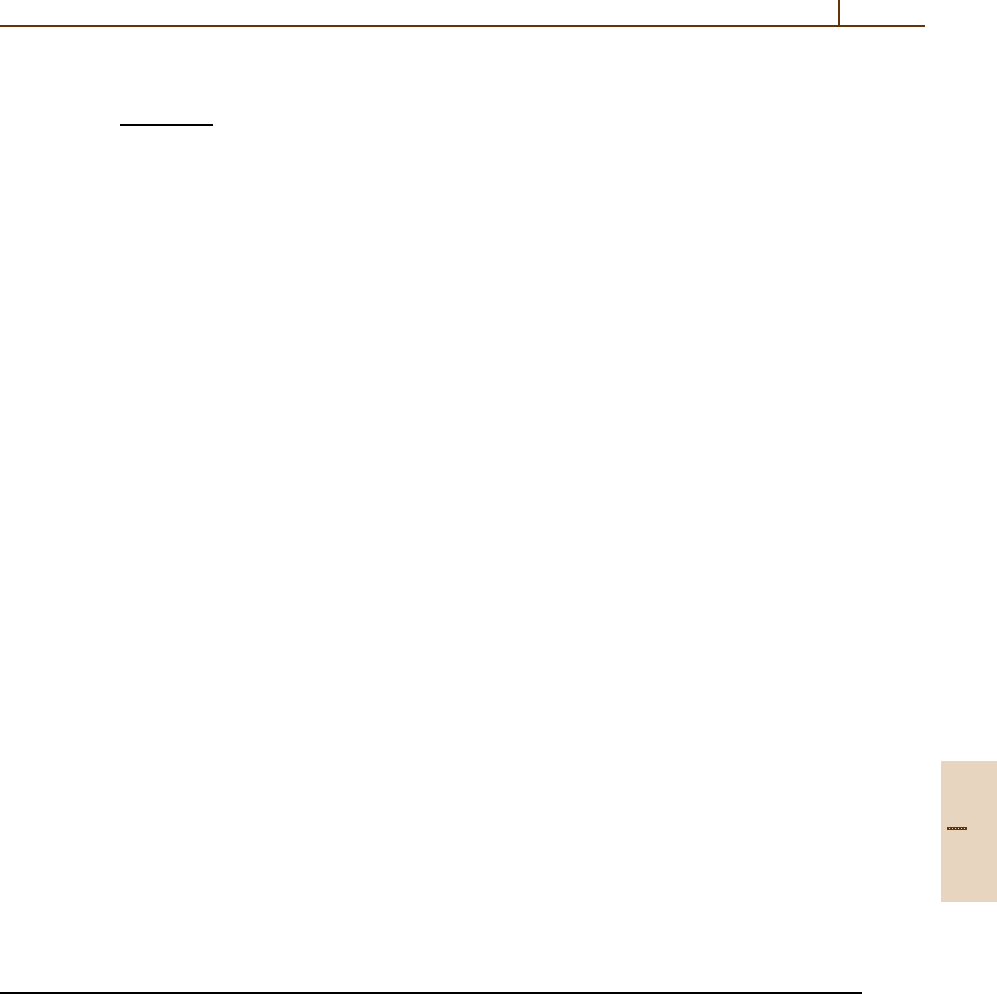
Orientation and Alignment in Atomic and Molecular Collisions References 703
figure,
tan γ
FBA
=
sin Θ
col
cos Θ
col
−x
,
(46.101)
where x =[E/(E −∆E)]
1/2
.For∆E > 0, γ
FBA
is al-
ways negative, with its minimum value when ∆k⊥ k
out
.
Any theoretical effort beyond the FBA involves serious
computations.
46.4 Recent Developments
46.4.1 S → D Excitation
The generalization of the formalism of Sect. 46.2.2 to
the case of S → D excitation involves the introduction
of three scattering amplitudes, corresponding to a com-
plete parameter set of one cross section, two relative
amplitude sizes, and two relative phases. Analysis shows
that a full coherence analysis of the light emitted in the
subsequent D → P optical decay is not sufficient for
a complete experiment, instead two solutions are ob-
tained. A triple coincidence experiment may resolve the
ambiguity [46.19].
46.4.2 P → P Excitation
By proper optical preparation of the atomic target,
collision studies involving specific excited states may
be performed as a function of scattering angle. For
collision-induced P → P transitions, a systematic prepa-
ration of specific initial P states, combined with Stokes
parameter analysis of the radiation pattern from the final
P state, may lead to a complete scattering experiment.
The corresponding complete set of nine parameters
describes the process in terms of five independent
scattering amplitudes. In addition to the charge cloud
shape and orientation parameters, three Euler angles
are needed to describe the atomic reference frame
of the charge cloud with respect to the laboratory
frame [46.20].
46.4.3 Relativistic Effects
in S → P Excitation
It has been discussed to what extent relativistic ef-
fects can be studied for excitation of the two fine
structure components of the resonance transitions of
heavy alkali atoms, such as Rb or Cs. For electron-
impact excitation, standard Stokes parameter analysis
turns out to be extremely insensitive to the inclu-
sion of relativistic effects in the numerical treatment,
which explains the success of nonrelativistic theories.
If spin-polarized electrons are used, either in the inci-
dent channel through measurement of spin asymmetries,
or in the final channels by performing a time-reversed
generalized Stokes parameter experiment with a laser-
prepared target and a spin-polarized electron beam,
distinct relativistic effects, typically at the 5% level, may
be revealed [46.21].
46.5 Summary
A selection of fundamental formulas describing ori-
entation and alignment in atomic collisions is given,
with emphasis on the simplest case, S → P excita-
tion. A tutorial introduction to the field with a series
of examples and applications may be found in a recent
textbook [46.22].
References
46.1 B. Bederson: Comments At. Mol. Phys. 1,41and65
(1969)
46.2 U.Fano,J.H.Macek:Rev.Mod.Phys.45, 553
(1973)
46.3 J. Kessler: Polarized Electrons (Springer, Berlin,
Heidelberg 1985)
46.4 I. V. Hertel, H. Schmidt, A. Bähring, E. Meyer: Rep.
Prog. Phys. 48, 375 (1985)
46.5 N. Andersen, J. W. Gallagher, I. V. Hertel: Phys. Rep.
165, 1 (1988)
46.6 N. Andersen, J. T. Broad, E. E. B. Campbell,
J. W. Gallagher, I. V. Hertel: Phys. Rep. 278,107
(1997)
46.7 N. Andersen, K. Bartschat, J. T. Broad, I. V. Hertel:
Phys. Rep. 279, 251 (1997)
46.8 U. Wille, R. Hippler: Phys. Rep. 132,129(1986)
Part D 46

704 Part D Scattering Theory
46.9 C. H. Greene, R. N. Zare: Ann. Rev. Phys. Chem. 33,
119 (1982)
46.10 K. Blum: Density Matrix Theory and Applications
(Plenum, New York 1981)
46.11 J. Macek, D. H. Jaecks: Phys. Rev. A 4, 2288 (1971)
46.12 M. Born, E. Wolf: Principles of Optics (Pergamon,
New York 1970)
46.13 K. Blum, F. T. da Paix
˜
ao, G. Csanak: J. Phys. B 13,
L257 (1980)
46.14 F. T. da Paix
˜
ao, N. T. Padial, Gy. Csanak, K. Blum:
Phys. Rev. Lett. 45, 1164 (1980)
46.15 I. V. Hertel, M. H. Kelley, J. J. McClelland: Z. Phys. D
6,163(1987)
46.16 N. Andersen, K. Bartschat: Comments At. Mol. Phys.
29, 157 (1993)
46.17 K. Bartschat: Phys. Rep. 180, 1 (1989)
46.18 N. Andersen, K. Bartschat: J. Phys. B 27, 3189
(1994); corrigendum N. Andersen, K. Bartschat:
J. Phys. B 29, 1149 (1996), see [46.23]
46.19 N. Andersen, K. Bartschat: J. Phys. B 30, 5071
(1997)
46.20 E. Y. Sidky, S. Grego, D. Dowek, N. Andersen:
J. Phys. B 35, 2005 (2002)
46.21 N. Andersen, K. Bartschat: J. Phys. 35,4507
(2002)
46.22 N. Andersen, K. Bartschat: Polarization, Alignment,
and Orientation in Atomic Collisions (Springer,
Berlin, Heidelberg 2001)
46.23 K. Muktavat, R. Srivastava, A. D. Stauffer: J. Phys. B
36, 2341 (2003)
Part D 46
705
Electron–Atom
47. Electron–Atom, Electron–Ion,
and Electron–Molecule
Collisions
This chapter reviews the theory of electron
collisions with atoms, ions and molecules.
Section 47.1 discusses elastic, inelastic and ionizing
collisions with atoms and atomic ions from close to
threshold to high energies where the Born series
becomes applicable. Section 47.2 extends the
theory to treat electron collisions with molecules.
Finally in Sect. 47.3 the theory of electron atom
collisions in intense laser fields is discussed. This
chapter will not present detailed comparisons
of theoretical predictions with experiment.
Such comparisons are given in recent review
articles [47.1–3]andinChapt.63.
47.1 Electron–Atom
and Electron–Ion Collisions .................. 705
47.1.1 Low-Energy Elastic Scattering
and Excitation .......................... 705
47.1.2 Relativistic Effects for Heavy
Atoms and Ions......................... 708
47.1.3 Multichannel Resonance Theory .. 710
47.1.4 Multichannel Quantum Defect
Theory ..................................... 711
47.1.5 Solution of the Coupled
Integrodifferential Equations...... 712
47.1.6 Intermediate and High Energy
Elastic Scattering and Excitation.. 714
47.1.7 Ionization ................................ 717
47.2 Electron–Molecule Collisions ................. 720
47.2.1 Laboratory Frame
Representation ......................... 720
47.2.2 Molecular Frame Representation . 721
47.2.3 Inclusion of the Nuclear Motion .. 722
47.2.4 Electron Collisions
with Polyatomic Molecules ......... 723
47.3 Electron–Atom Collisions
in a Laser Field.................................... 723
47.3.1 Potential Scattering ................... 724
47.3.2 Scattering by Complex Atoms
and Ions .................................. 725
References .................................................. 727
47.1 Electron–Atom and Electron–Ion Collisions
47.1.1 Low-Energy Elastic Scattering
and Excitation
In this section we consider the process
e
−
+ A
i
→ e
−
+ A
j
, (47.1)
where A
i
and A
j
are bound states of the target atom or
ion and where the velocity of the incident or scattered
electron is of the same order or less than that of the target
electrons actively involved in the collision.
Assume initially that all relativistic effects can
be neglected, which restricts the treatment to low-Z
atoms and ions. The Schrödinger equation describ-
ing the scattering of an electron by a target atom or
ion containing N electrons and nuclear charge Z is
then
H
N+1
Ψ = EΨ, (47.2)
where E is the total energy of the system. The (N + 1)-
electron nonrelativistic Hamiltonian H
N+1
is given in
atomic units by
H
N+1
=
N+1
i=1
−
1
2
∇
2
i
−
Z
r
i
+
N+1
i> j=1
1
r
ij
, (47.3)
where r
ij
=|r
i
−r
j
|,andr
i
and r
j
are the vector co-
ordinates of electrons i and j relative to the origin of
coordinates taken to be the target nucleus, which is
assumed to have infinite mass.
The target eigenstates Φ
i
and the corresponding
eigenenergies w
i
satisfy the equation
Φ
i
|H
N
|Φ
j
=w
i
δ
ij
, (47.4)
where H
N
is defined by (47.3) with N + 1 replaced by N.
The calculation of accurate target states is discussed in
Chapt. 21. The solution of (47.2), corresponding to the
Part D 47
706 Part D Scattering Theory
process (47.1), then has the asymptotic form
Ψ
i
≈
r→∞
Φ
i
χ
1
2
m
i
e
ik
i
z
+
j
Φ
j
χ
1
2
m
j
f
ji
(
θ, φ
)
e
ik
j
r
.
(47.5)
In (47.5), χ
1
2
m
i
and χ
1
2
m
j
are the spin eigenfunctions of
the incident and scattered electrons, where the direction
of spin quantization is usually taken to be the incident
beam direction, and f
ji
(θ, φ) is the scattering amplitude,
the spherical polar coordinates of the scattered electron
being denoted by r, θ and φ. Also the wave numbers
k
i
and k
j
are related to the total energy of the system
by
E = w
i
+
1
2
k
2
i
= w
j
+
1
2
k
2
j
. (47.6)
The outgoing wave term in (47.5) contains contribu-
tions from all target states that are energetically allowed;
i. e., for which k
2
j
≥ 0. If the energy is above the ioniza-
tion threshold, this includes target continuum states. For
an atomic ion, a logarithmic phase factor is also needed
as discussed below.
The differential cross section for a transition from
an initial state |i=
k
i
,Φ
i
,χ
1
2
m
i
to a final state
| j=|k
j
,Φ
j
,χ
1
2
m
j
is given by
dσ
ji
dΩ
=
k
j
k
i
| f
ji
(
θ, φ
)
|
2
, (47.7)
and the total cross section is obtained by averaging over
initial spin states, summing over final spin states and
integrating over all scattering angles.
In order to solve the Schrödinger equation to obtain
the scattering amplitude and cross section at low ener-
gies, we make a partial wave expansion of the total wave
function
Ψ
Γ
j
(
X
N+1
)
= A
n
i=1
Φ
Γ
i
x
1
,... ,x
N
;
ˆ
r
N+1
σ
N+1
× r
−1
N+1
F
Γ
ij
(
r
N+1
)
+
m
i=1
χ
Γ
i
(
x
1
,... ,x
N+1
)
b
Γ
ij
, (47.8)
where X
N+1
≡ x
1
, x
2
···x
N+1
represents the space and
spin coordinates of all N + 1 electrons, x
i
≡ r
i
σ
i
repre-
sents the space and spin coordinates of the ith electron
and A is the operator that antisymmetrizes the first sum-
mation with respect to exchange of all pairs of electrons
in accordance with the Pauli exclusion principle. The
channel functions Φ
Γ
i
, assumed to be n in number, are
obtained by coupling the orbital and spin angular mo-
menta of the target states Φ
i
with those of the scattered
electron to form eigenstates of the total orbital and spin
angular momenta, their z components and the parity π,
where
Γ ≡ LM
L
SM
S
π (47.9)
is conserved in the collision. The square integrable cor-
relation functions χ
Γ
i
allow for additional correlation
effects not included in the first expansion in (47.8)that
goes over a limited number of target eigenstates, and
possibly pseudostates.
By substituting (47.8) into the Schrödinger equa-
tion (47.2), projecting onto the channel functions
Φ
Γ
i
and onto the square integrable functions χ
Γ
i
,and
eliminating the coefficients b
Γ
ij
, we obtain n coupled
integrodifferential equations satisfied by the reduced
radial functions F
Γ
ij
representing the motion of the
scattered electron of the form
d
2
dr
2
−
i
(
i
+ 1
)
r
2
+
2(Z − N)
r
+ k
2
i
F
Γ
ij
(
r
)
= 2
V
Γ
i
(
r
)
F
Γ
j
(
r
)
+
∞
0
K
Γ
i
r, r
+ X
Γ
i
r, r
F
Γ
j
r
dr
.
(47.10)
Here
i
is the orbital angular momentum of the scat-
tered electron, and V
Γ
i
, W
Γ
i
and X
Γ
i
are the local direct,
nonlocal exchange and nonlocal correlation potentials
respectively. If the correlation potential which arises
from the χ
Γ
i
terms in (47.8) is not included, then (47.10)
are called the close coupling equations.
The direct potential can be written as
V
Γ
ij
(
r
N+1
)
=
Φ
Γ
i
x
1
,... ,x
N
;
ˆ
r
N+1
σ
N+1
×
N
i=1
1
r
iN+1
−
N
r
N+1
×
Φ
Γ
j
x
1
,... ,x
N
;
ˆ
r
N+1
σ
N+1
,
(47.11)
where the integral is taken over all electron space and
spin coordinates, except the radial coordinate of the
Part D 47.1

Electron–Atom, Electron–Ion, and Electron–Molecule Collisions 47.1 Electron–Atom and Electron–Ion Collisions 707
(N + 1)th electron. This potential has the asymptotic
form
V
Γ
ij
(r) =
λ max
λ=1
a
λ
ij
r
−λ−1
, r ≥ a (47.12)
where a is the range beyond which the orbitals in the
target states Φ
i
included in the first expansion in (47.8),
are negligible. The λ = 1termin(47.12)givesrise,in
second-order, to the long-range attractive polarization
potential
V
(
r
)
→
r→∞
−
1
2
α
r
4
(47.13)
seen by an electron incident on an atom. For an s-state
atom in a state Φ
0
the dipole polarizability α is given by
α = 2
j
Φ
0
|
4π
3
1/2
N
i=1
r
i
Y
10
ˆ
r
i
|Φ
j
2
w
j
− w
0
.
(47.14)
These long-range potentials have a profound influence
on low-energy scattering.
The exchange and correlation potentials, unlike the
direct potential, are both nonlocal and the exchange
potential vanishes exponentially for large r. Explicit
expressions for these potentials are too complicated to
write down, except in the case of e
−
–H scattering where
the direct and exchange potentials were first given by
Percival and Seaton [47.4]. Instead they are determined
by general computer programs.
The scattering amplitude and cross section can be
obtained by solving (47.10) for all relevant conserved
quantum numbers Γ subject to the following K-matrix
asymptotic boundary conditions
F
Γ
ij
≈
r→∞
k
−
1
2
i
sin θ
i
δ
ij
+ cos θ
i
K
Γ
ij
,
open channels k
2
i
≥ 0
F
Γ
ij
≈
r→∞
0 ,
closed channels k
2
i
< 0 (47.15)
where
θ
i
= k
i
r −
1
2
i
π +
z
k
i
ln
(
2k
i
r
)
+ σ
i
(47.16)
with z = Z − N,andσ
i
= arg Γ(
i
+ 1 − iz/k
i
).The
S-matrix and T-matrix are related to the K-matrix de-
fined by (47.15) by the matrix equations
S
Γ
=
I+ iK
Γ
I− iK
Γ
, T
Γ
= S
Γ
− I =
2iK
Γ
I− iK
Γ
,
(47.17)
where the dimensions of the matrices in these equations
are n
a
× n
a
,wheren
a
is the number of open channels
at the energy under consideration for the given Γ .The
Hermiticity and time reversal invariance of the Hamil-
tonian ensures that K
Γ
is real and symmetric, and S
Γ
is
unitary and symmetric.
The scattering amplitude defined by (47.5) can be ex-
pressedintermsoftheT-matrix elements. For a neutral
target,
f
ji
(
θ, φ
)
= i
π
k
i
k
j
1
2
LSπ
i
j
i
i
−
j
(
2
i
+ 1
)
1
2
×
L
i
M
L
i
i
0|L
i
i
LM
L
×
S
i
M
S
i
1
2
m
i
|S
i
1
2
SM
S
× (L
j
M
L
j
j
m
j
|L
j
j
LM
L
)
×
S
j
M
S
j
1
2
m
j
|S
j
1
2
SM
S
T
Γ
ji
Y
j
m
j
(
θ, φ
)
,
(47.18)
which describes a transition from an initial state
α
i
L
i
S
i
M
L
i
M
S
i
m
i
to a final state α
j
L
j
S
j
M
L
j
M
S
j
m
j
,
where α
i
and α
j
represent any additional quantum
numbers required to completely define the initial and
final states. The corresponding total cross section, ob-
tained by averaging over the initial magnetic quantum
numbers, summing over the final magnetic quantum
numbers, and integrating over all scattering angles,
is
σ
tot
(
i → j
)
=
π
k
2
i
LSπ
i
j
(
2L + 1
)(
2S+ 1
)
2
(
2L
i
+ 1
)(
2S
i
+ 1
)
T
Γ
ji
2
,
(47.19)
which describes a transition from an initial target state
α
i
L
i
S
i
to a final target state α
j
L
j
S
j
. In applications, it
is also useful to define a collision strength by
Ω
(
i, j
)
= k
2
i
(
2L
i
+ 1
)(
2S
i
+ 1
)
σ
tot
(
i → j
)
,
(47.20)
which is dimensionless and symmetric with respect to
interchange of the intial and final states denoted by
i and j. For scattering by an ion, the above expres-
sion for f
ji
(
θ, φ
)
is modified by the inclusion of the
Coulomb scattering amplitude when the initial and final
states are identical.
For incident electron energies insufficient to excite
the atom or ion, only elastic scattering is possible and the
Part D 47.1
708 Part D Scattering Theory
above expressions simplify. Consider low energy elastic
electron scattering by a neutral atom is a
1
S ground state.
Then the expression for the scattering amplitude (47.18)
reduces to
f
(
θ
)
=
1
2ik
∞
=0
(
2 + 1
)
e
2iδ
− 1
P
(
cos θ
)
,
(47.21)
where
= L =
i
=
j
is the angular momentum of
the scattered electron, k is its wave number, and the
phase shift δ
can be expressed in terms of the K-
matrix, which now has only one element since n
a
= 1,
by
tan δ
= K
Γ
11
. (47.22)
The corresponding expression for the total cross section
is then
σ
tot
=
4π
k
2
∞
=0
(
2 + 1
)
sin
2
δ
. (47.23)
A diffusion, or momentum transfer cross section, can
also be defined as
σ
D
= 2π
π
0
| f
(
θ
)
|
2
(
1 − cos θ
)
sin θ dθ
=
4π
k
2
∞
=0
(
+ 1
)
sin
2
(
δ
+1
− δ
)
,
(47.24)
which is important when considering the diffusion of
electrons through gases.
At low incident electron energies, the behav-
ior of the phase shift for an atom in a s -state is
dominated by the long-range polarization potential
(47.13). O’Malley et al. [47.5] showed that for s-
wave scattering k cot δ
0
satisfies the effective range
expansion
k cot δ
0
=−
1
a
s
+
πα
3a
2
s
k
+
2α
3a
s
k
2
ln
αk
2
16
+ O
k
2
,
(47.25)
where a
s
is the scattering length, while for ≥ 1
k
2
cot δ
=
8
+
3
2
+
1
2
−
1
2
πα
+··· .
(47.26)
It follows that close to threshold, the total elastic cross
section has the form
σ
tot
= 4πa
2
s
+
8
3
π
2
αa
s
k+··· . (47.27)
When an electron is elastically scattered by a positive
or negative ion, then these formulae for the low-energy
behavior of the phase shift are modified. For scattering
by a positive ion, Seaton [47.6]hasshownthat
cot δ
(
k
)
1 − e
2πη
= cot
πµ
k
2
,
(47.28)
where η =−z/k,andwhereµ
k
2
is the analytic contin-
uation of the quantum defects of the electron–ion bound
states to positive energies. This quantum defect theory
enables spectroscopic observations of bound state en-
ergies to be extrapolated to positive energies to yield
electron–ion scattering phase shifts. For a negative ion,
where the Coulomb potential is repulsive, the phase shift
behaves as
δ
→
k→0
exp(2πz/k), (47.29)
which vanishes rapidly as k tends to zero since z is now
negative.
47.1.2 Relativistic Effects for Heavy Atoms
and Ions
As the nuclear charge Z of the target increases, rela-
tivistic effects become important even for low energy
scattering. There are two ways in which relativistic
effects play a role. First, there is a direct effect cor-
responding to the relativistic distortion of the wave
function describing the scattered electron by the strong
nuclear Coulomb potential. Second, there is an indirect
effect caused by the change in the charge distribution of
the target due to the use of relativistic wave functions
discussed in Chapt. 22. We will concentrate on the direct
effect in this section.
For atoms and ions with small Z,theK-matrices can
first be calculated in LS coupling, neglecting relativis-
tic effects. The K-matrices are then recoupled to yield
transitions between fine-structure levels. We introduce
the pair-coupling scheme
L
i
+ S
i
= J
i
, J
i
+
i
= K
i
, K
i
+ s = J ,
(47.30)
where J
i
is the total angular momentum of the target,
i
is the orbital angular momentum of the scattered elec-
tron, s is its spin, and J is the total angular momentum,
which with the parity π is conserved in the collision.
Part D 47.1

Electron–Atom, Electron–Ion, and Electron–Molecule Collisions 47.1 Electron–Atom and Electron–Ion Collisions 709
The transition from LS coupling involves the recoupling
coefficient
[
(
L
i
S
i
)
J
i
,
i
]K
i
,
1
2
; JM
J
|
(
L
i
i
)
L,
S
i
1
2
S; JM
J
=
[
(
2J
i
+ 1
)(
2L + 1
)(
2K
i
+ 1
)(
2S+ 1
)
]
1
2
× W
(
L
i
S
i
J
i
; L
i
K
i
)
W
LJS
i
1
2
; SK
i
,
(47.31)
and the corresponding K-matrix transforms as
K
Jπ
ij
=
LS
((
L
i
S
i
)
J
i
,
i
)
K
i
,
1
2
;
×JM
J
|
(
L
i
i
)
L,
S
i
1
2
S; JM
J
× K
Γ
ij
×
L
j
j
L,
S
j
1
2
S;
×JM
J
|
L
j
S
j
J
j
,
j
K
j
,
1
2
; JM
J
.
(47.32)
This transformation has been implemented in a computer
program by Saraph [47.7, 8].
For intermediate-Z atoms and ions, relativistic
effects can be included by adding terms from the Breit–
Pauli Hamiltonian to the nonrelativistic Hamiltonian
(Jones [47.9], Scott and Burke [47.10]). We write
H
BP
N+1
= H
nr
N+1
+ H
rel
N+1
(47.33)
where H
nr
N+1
is defined by (47.3)andH
rel
N+1
consists
of one- and two-body relativistic terms. The one-body
terms are (Sect. 21.1)
H
mass
N+1
=−
1
8
α
2
N+1
i=1
∇
4
i
mass-correction term ,
H
D
1
N+1
=−
1
8
α
2
Z
N+1
i=1
∇
2
i
1
r
i
one-body Darwin term ,
H
so
N+1
=
1
2
α
2
N+1
i=1
1
r
i
∂V
∂r
i
(
i
· s
i
)
spin–orbit term .
The two-body terms are less important and are usually
not included in collision calculations.
The modified Schrödinger equation defined by
(47.2), with H
N+1
replaced by H
BP
N+1
, is solved by adopt-
ing an expansion similar in form to (47.8), but now using
the pair coupling scheme in the definition of the chan-
nel functions and quadratically integrable functions. We
then obtain coupled integrodifferential equations similar
in form to (47.10), from which the K-matrix, S-matrix
and T-matrix can be obtained. The corresponding total
cross section in the pair-coupling scheme analogous to
(47.19)is
σ
tot
(
i → j
)
=
π
2k
2
i
(
2J
i
+ 1
)
Jπ
K
i
K
j
i
j
(
2J + 1
)
T
Jπ
ji
2
,
(47.34)
which describes a transition from an initial target state
α
i
J
i
to a final target state α
j
J
j
. The corresponding
collision strength is
Ω
(
i, j
)
= k
2
i
(
2J
i
+ 1
)
σ
tot
(
i → j
)
.
(47.35)
For high-Z atoms and ions, the Dirac Hamilto-
nian [47.11, 12] (Sect. 47.2)
H
D
N+1
=
N+1
i=1
cα · p
i
+ β
c
2
−
Z
r
i
+
N+1
i> j=1
1
r
ij
(47.36)
must be used instead of (47.3), where β
= β − 1and
α and β are the usual Dirac matrices. The expansion of
the total wave functions for a particular JM
J
π takes the
general form of (47.8). However, now both the bound
orbitals in the target, and correlation functions and the
orbitals representing the scattered electron are repre-
sented by Dirac orbitals. These are defined in terms of
large and small components P(r) and Q(r) by
φ
(
r,σ
)
=
1
r
P
a
(
r
)
χ
κm
ˆ
r,σ
Q
a
(
r
)
χ
−κm
ˆ
r,σ
(47.37)
for the bound orbitals, and
F
(
r,σ
)
=
1
r
P
c
(
r
)
χ
κm
ˆ
r,σ
Q
c
(
r
)
χ
−κm
ˆ
r,σ
(47.38)
for the continuum orbitals, where a = nκm, c = kκm and
the spherical spinor
χ
κm
ˆ
r,σ
=
m
m
i
m
1
2
m
i
|
1
2
jm
Y
m
(
θ, φ
)
χ
1
2
m
i
(
σ
)
,
(47.39)
where κ = j +
1
2
when = j +
1
2
,andκ =−j −
1
2
when
= j −
1
2
. We can now derive coupled integrodiffer-
ential equations for the functions P
c
(
r
)
and Q
c
(
r
)
Part D 47.1
710 Part D Scattering Theory
in a similar way to the derivation of (47.10), except
that these are now coupled first-order equations instead
of coupled second-order equations. The K-matrix, and
hence the S-matrix and T-matrix, can be obtained from
the asymptotic form of these equations. The total cross
section in the j– j coupling scheme, is then given by
(47.34), and the corresponding collision strength is given
by (47.35).
47.1.3 Multichannel Resonance Theory
General resonance theories have been developed by
Fano [47.13, 14], Feshbach [47.15, 16], and Brenig and
Haag[47.17].TheyarealsodiscussedinChapt.25.Here
we will limit our discussion to the effect that resonances
have on electron collision cross sections.
Following Feshbach, we introduce the projection op-
erators P and Q,whereP projects onto a finite set of
low energy channels in (47.8)andQ projects onto the
orthogonal space, where we restrict our consideration to
the space corresponding to a particular set of conserved
quantum numbers Γ . In this space we have
P
2
= P, Q
2
= Q, P + Q = 1 . (47.40)
The Schrödinger equation (47.2) can then be written as
P
(
H − E
)(
P + Q
)
Ψ = 0
(47.41)
and
Q
(
H − E
)(
P + Q
)
Ψ = 0
(47.42)
where we have omitted the subscript N + 1onH and
the superscript Γ on Ψ . After solving (47.42)forQΨ
and substituting into (47.41), we find that
P
H − PHQ
1
Q
(
H − E
)
Q
QHP− E
PΨ = 0 ,
(47.43)
where the term
V
op
=−PHQ
1
Q
(
H − E
)
Q
QHP ,
(47.44)
called the optical potential, allows for propagation in
the Q-space channels.
We now introduce the eigenfunctions φ
i
and eigen-
values ε
i
of the operator QHQby
QHQφ
i
= ε
i
φ
i
. (47.45)
It follows that the discrete eigenvalues ε
i
each give rise to
poles in V
op
at ε
i
. If the energy E is in the neighborhood
of an isolated pole or bound state ε
i
, we can rewrite
(47.43)as
PHP−
j=i
PHQ
|φ
j
φ
j
|
ε
j
− E
QHP− E
PΨ
= PHQ
|φ
i
φ
i
|
ε
i
− E
QHPΨ,
(47.46)
where the rapidly varying part of the optical potential
has been separated and put on the right-hand-side of
(47.46). This equation can be solved by introducing the
Green’s function G
0
and the solutions ψ
0 j
of the opera-
tor on the left-hand side of (47.46). We find that the pole
term on the right-hand side of this equation gives rise to
a Feshbach resonance whose position is
E
i
= ε
i
+ ∆
i
−
1
2
iΓ
i
= E
i,r
−
1
2
iΓ
i
, (47.47)
is where the resonance shift
∆
i
=φ
i
|QHPG
0
PHQ|φ
i
, (47.48)
and the resonance width is
Γ
i
= 2π
j
|φ
i
| QHP | ψ
0 j
|
2
, (47.49)
where the summation in this equation is taken over all
continuum states corresponding to the operator on the
left-hand-side of (47.46) and these states are normalized
to a delta function in energy.
In the neighborhood of the resonance energy E
i,r
,
the S-matrix is rapidly varying with the form
S= S
1
2
0
I− iΓ
γ
i
× γ
i
E − E
i,r
+
1
2
iΓ
i
S
1
2
0
, (47.50)
where S
0
is the slowly varying nonresonant or back-
ground S-matrix corresponding to ψ
0
, and the partial
widths γ
i
are defined by
φ
i
| QHP | ψ
0
=Γ
1
2
i
γ
i
· S
1
2
0
, (47.51)
where γ
i
· γ
i
= 1. A corresponding resonant expression
can be derived for the K-matrix (Burke [47.18]).
Let us now diagonalize the S-matrix as follows:
S= Aexp
(
2i∆
)
A
T
, (47.52)
where A is an orthogonal matrix and ∆ is a diago-
nal matrix whose diagonal elements, δ
i
, i = 1,... , n
a
,
are called the eigenphases. If we define the eigenphase
sum δ
sum
by
δ
sum
=
n
a
i=1
δ
i
, (47.53)
Part D 47.1
