Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics

Подождите немного. Документ загружается.

234 Part B Atoms

creased the number of known astronomical objects, but

also motivated the study of the effects of strong ﬁelds

on heavier atoms [13.20].

Another interesting area of current research con-

cerns the relationship between quantum mechanics and

classically chaotic systems. For these studies, Rubid-

ium Rydberg atoms are an ideal system since laboratory

ﬁelds can easily push the atom to the strong-ﬁeld

limit [13.21–23].

For a very useful review of various topics up to 1998

see [13.24]; a more concise review, concerning the elec-

tronic structure of atoms, molecules, and bulk matter,

including some properties of dense plasma, in strong

ﬁelds, is given in [13.25].

References

13.1 L. D. Landau, E. M. Lifshitz: Quantum Mechanics

(Course of Theoretical Physics), Vol. 3 (Pergamon,

Oxford 1977) p. 456

13.2 L. D. Landau, E. M. Lifshitz: The Classical Theory of

Fields (Course of Theoretical Physics), Vol. 2 (Perga-

mon, Oxford 1975) p. 49

13.3 A. Messiah: Quantum Mechanics (Wiley, New York

1999) p. 491

13.4 C. Itzykson, J.-B. Zuber: Quantum Field Theory

(McGraw-Hill, New York 1980) p. 67

13.5 H. A. Bethe, E. Salpeter: Quantum Mechanics of

One- and Two-electron Atoms (Plenum, New York

1977) p. 208

13.6 H. A. Bethe, E. Salpeter: Quantum Mechanics of

One- and Two-electron Atoms (Plenum, New York

1977) p. 211

13.7 Z. Chen, S. P. Goldman: Phys. Rev. A 48, 1107

(1993)

13.8 H. A. Bethe, E. Salpeter: Quantum Mechanics of

One- and Two-electron Atoms (Plenum, New York

1977) p. 229

13.9 H. A. Bethe, E. Salpeter: Quantum Mechanics of

One- and Two-electron Atoms (Plenum, New York

1977) p. 233

13.10 G. W. F. Drake, S. P. Goldman: Phys. Rev. A 23,2093

(1981)

13.11 G. W. F. Drake: Phys. Rev. A 45, 70 (1992)

13.12 S. P. Goldman: Phys. Rev. A 50, 3039 (1994)

13.13 S. P. Goldman, G. W. F. Drake: Phys. Rev. Lett. 68,

1683 (1992)

13.14 R. González-Férez, J. S. Dehesa: Phys. Rev. Lett. 91,

113001 (2003)

13.15 C. E. Shannon: Bell Syst. Tech. J. 27, 623 (1948)

13.16 W. Becken, P. Schmelcher, F. K. Diakonos: J. Phys.

B. 32, 1557 (1999)

13.17 W. Becken, P. Schmelcher: Phys. Rev. A 63,053412

(2001)

13.18 W. Becken, P. Schmelcher: Phys. Rev. A 65, 033416

(2002)

13.19 S. Jordan, P. Schmelcher, W. Becken, W. Schweizer:

Astron. Astrophys. 336, 33 (1998)

13.20 P. Schmelcher: private communication

13.21 J. von Milczewski, T. Uzer: Atoms and Molecules in

Strong External Fields, edited by P. Schmelcher and

W. Schweizer (Springer, Berlin, Heidelberg 1998)

p. 199

13.22 J. Main, G. Wunner: Atoms and Molecules in

Strong External Fields, edited by P. Schmelcher and

W. Schweizer (Springer, Berlin, Heidelberg 1998)

p. 223

13.23 J. R. Guest, G. Raithel: Phys. Rev. A 68, 052502

(2003)

13.24 P. Schmelcher, W. Schweizer (Eds.): Atoms and

Molecules in Strong External Fields (Springer, Berlin

1998)

13.25 D. Lai: Ref. Mod. Phys 73, 629 (2001)

Part B 13

235

Rydberg Atom

14. Rydberg Atoms

Rydberg atoms are those in which the valence

electron is in a state of high principal quantum

number n. They are of historical interest since the

observation of Rydberg series helped in the initial

unraveling of atomic spectroscopy [14.1]. Since

the 1970s, these atoms have been studied mostly

for two reasons. First, Rydberg states are at the

border between bound states and the continuum,

and any process which can result in either excited

bound states or ions and free electrons usually

leads to the production of Rydberg states. Second,

the exaggerated properties of Rydberg atoms allow

experimentstobedonewhichwouldbedifﬁcult

or impossible with normal atoms.

14.1 Wave Functions

and Quantum Defect Theory ................. 235

14.2 Optical Excitation

and Radiative Lifetimes ....................... 237

14.3 Electric Fields ...................................... 238

14.4 Magnetic Fields ................................... 241

14.5 Microwave Fields ................................. 242

14.6 Collisions ............................................ 243

14.7 Autoionizing Rydberg States ................. 244

References .................................................. 245

14.1 Wave Functions and Quantum Defect Theory

Many of the properties of Rydberg atoms can be cal-

culated accurately using quantum defect theory, which

is easily understood by starting with the H atom [14.2].

We shall use atomic units, as discussed in Sect. 1.2.The

Schrödinger equation for the motion of the electron in

a H atom in spherical co-ordinates is



−

∇

−



Ψ(r,θ,φ)= EΨ(r,θ,φ),

(14.1)

where E is the energy, r is the distance between the

electron and the proton, and θ and φ are the polar

and azimuthal angles of the electron’s position. Equa-

tion (14.1) can be separated, and its solution expressed

as the product

Ψ(r,θ,φ)= R(r)Y

m

(θ, φ) , (14.2)

where  and m are the orbital and azimuthal-orbital

angular momentum (i. e., magnetic) quantum numbers

and Y

m

(θ, φ) is a normalized spherical harmonic. R(r)

satisﬁes the radial equation

R(r)

2dR(r)

r dr

+2ER(r)+

2R(r)

( + 1)R

(14.3)

which has the two physically interesting solutions

R(r) =

f(, E, r)

(14.4)

R(r) =

g(, E, r)

(14.5)

The f and g functions are the regular and irregular

Coulomb functions which are the solutions to a variant

of (14.3). As r → 0 they have the forms [14.3]

f (, E, r) ∝ r

+1

, (14.6)

g(, E, r) ∝ r

−

, (14.7)

irrespective of whether E is positive or negative. As

r →∞,forE > 0the f and g functions are sine and

cosine waves, i. e., there is a phase shift of π/2 between

them. For E < 0 it is useful to introduce ν,deﬁnedby

E =−1/2ν

,andforE < 0asr →∞

f = u(, ν, r) sin πν − v(, ν, r)e

iπν

, (14.8)

g =−u(, ν, r) cos πν + v(, ν, r)e

iπ(ν+1/2)

(14.9)

where u and v are exponentially increasing and decreas-

ing functions of r.Asr →∞, u →∞and v → 0.

Part B 14

236 Part B Atoms

Requiring that the wave function be square inte-

grable means that as r → 0 only the f function is

allowed. Equation (14.8) shows that the r →∞bound-

ary condition requires that sin πν be zero or ν an

integer n, leading to the hydrogenic Bohr formula for

the energies:

E =−

. (14.10)

The classical turning point of an s wave occurs at

r = 2n

, and the expectation values of positive pow-

ers of r reﬂect the location of the outer turning point,

i. e.,





≈ n

. (14.11)

The expectation values of negative powers of r are

determined by the properties of the wave function at

small r. The normalization constant of the radial wave

function scales as n

−3/2

,sothatR(r) ∝ n

−3/2

+1

for small r. Accordingly, the expectation values of

negative powers of r, except r

−1

, and any prop-

erties which depend on the small r part of the

wave function, scale as n

−3

. Using the properties

of the wave function and the energies, the n-

scaling of the properties of Rydberg atoms can be

determined.

The primary reason for introducing the Coulomb

waves instead of the more common Hermite poly-

nominal solution for the radial function is to set the

stage for single channel quantum defect theory, which

enables us to calculate the wave functions and prop-

erties of one valence electron atoms such as Na. The

simplest picture of an Na Rydberg atom is an elec-

tron orbiting a positively charged Na

core consisting

of 10 electrons and a nucleus of charge +11. The

ten electrons are assumed to be frozen in place with

spherical symmetry about the nucleus, so their charge

cloud is not polarized by the outer valence electron,

although the valence electron can penetrate the ten-

electron cloud. When the electron penetrates the charge

cloud of the core electrons, it sees a potential well

deeper than −1/r due to the decreased shielding of the

+11 nuclear charge. For Na and other alkali atoms, we

assume that there is a radius r

such that for r < r

the potential is deeper than −1/r,andforr > r

is equal to −1/r. As a result of the deeper potential

at r < r

, the radial wave function is pulled into the

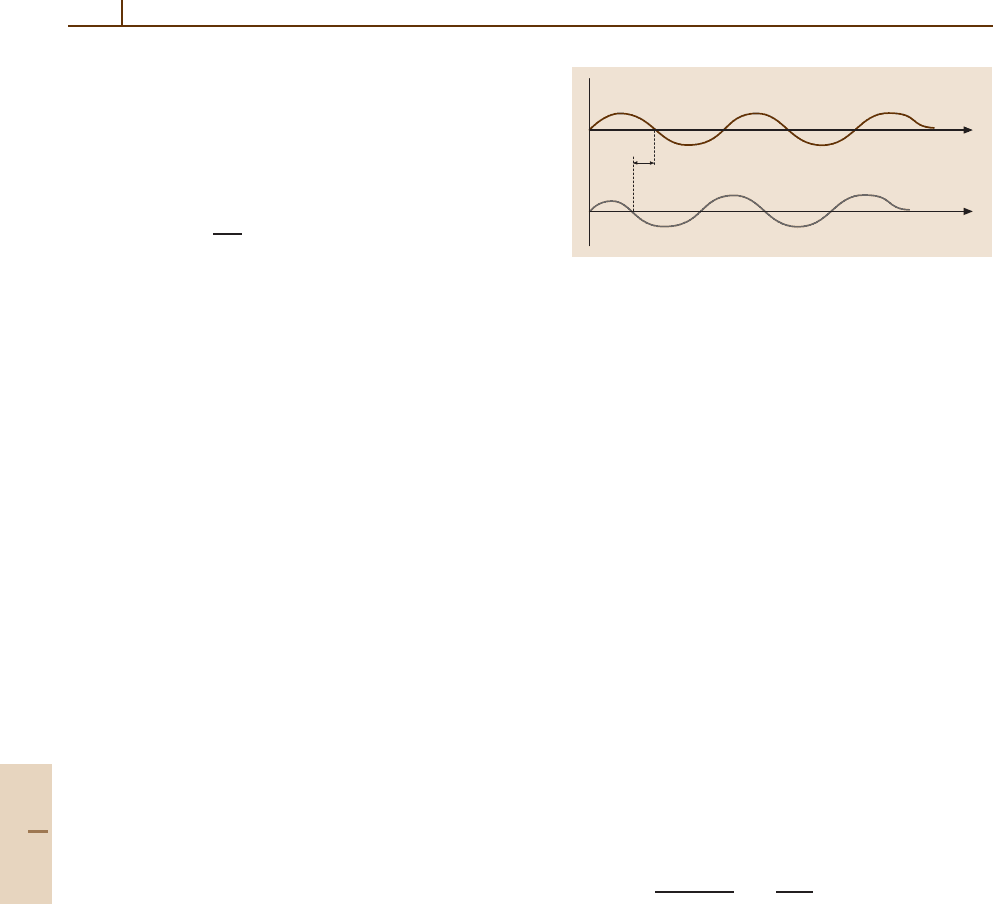
core in Na, relative to H, as shown in Fig. 14.1.For

r ≥ r

, the potential is a Coulomb −1/r potential, and

R(r) is a solution of (14.3) which can be expressed

Hydrogen

Sodium

Fig. 14.1 Radial wave functions for H and Na showing that

the Na wave function is pulled in toward the ionic core

R(r) =



f (, ν, r) cos τ



− g(, ν, r) sin τ





r ,

(14.12)

where τ



is the radial phase shift.

Near the ionization limit, E ∼ 0, and as a result,

the kinetic energy of the Rydberg electron is greater

than 1/r

(∼ 10 eV) when r < r

. As a result, changes

in E of 0.10 eV, the n = 10 binding energy, do not

appreciably alter the phase shift τ



, and we can as-

sume τ



to be independent of E.The dependence

of τ



arises because the centrifugal ( + 1)/r term in

(14.3) excludes the Rydberg electron from the region

of the core in states of high . Applying the r →∞

boundary condition to the wave function of (14.12)

leads to the requirement that the coefﬁcient of u vanish,

i. e.,

cos τ



sin(πν) + sin τ



cos(πν) = 0 , (14.13)

which implies that sin(πν + τ



) = 0orν = n − τ



/π.

Usually τ



/π is written as δ



and termed the quantum

defect, and the energies of members of the n series are

written as

E =−

2(n− δ



)

=−

∗2

, (14.14)

where n

∗

= n− δ



is often termed the effective quantum

number (see also Sect. 11.4.1).

Knowledge of the quantum defect δ



of a se-

ries of  states determines their energies, and it is

a straightforward matter to calculate the Coulomb wave

function speciﬁed in (14.12) using a Numerov algo-

rithm [14.4, 5]. This procedure gives wave functions

valid for r ≥ r

, which can be used to calculate many

of the properties of Rydberg atoms with great accu-

racy. The effect of core penetration on the energies is

easily seen in the energy level diagram of Fig. 14.2.

The Na  ≥ 2 states have the same energies as hydro-

Part B 14.1

Rydberg Atoms 14.2 Optical Excitation and Radiative Lifetimes 237

–10

–20

–30

–40

Sodium Hydrogen

E (× 1000 cm

–1

)

n =8

n =4

n =3

n =2

Fig. 14.2 Energy levels of Na and H

gen, while the s and p states, with quantum defects of

1.35 and 0.85 respectively, lie far below the hydrogenic

energies.

Although it is impossible to discern in Fig. 14.2,

the Na  ≥ 2 states also lie below the hydrogenic

energies. For these states it is not core penetration,

but core polarization which is responsible for the

shift to lower energy. Contrary to our earlier as-

sumption that the outer electron does not affect the

inner electrons if r > r

, the outer electron polar-

izes the inner electron cloud even when r > r

,and

the energies of even the high  states fall below the

hydrogenic energies. The leading term in the polariza-

tion energy is due to the dipole polarizability of the

core, α

. For high  states it gives a quantum defect

of [14.6]



3α

4

. (14.15)

Quantum defects due primarily to core polarization

rarely exceed 10

−2

, while those due to core penetration

are often greater than one.

14.2 Optical Excitation and Radiative Lifetimes

Optical excitation of the Rydberg states from the ground

state or any other low lying state is the continuation of

the photoionization cross section σ

below the ioniza-

tion limit. The photoionization cross section, discussed

more extensively in Chapt. 24, is approximately con-

stant at the limit. Above and below the limit the average

photoabsorption cross section is the same, as evidenced

by the fact that a discontinuity is not evident in an ab-

sorption spectrum, i. e., it is not possible to see where

the unresolved Rydberg states end and the continuum

begins. Nonetheless, below the limit the cross section

is structured by the ∆n spacing of 1/n

between adja-

cent members of the Rydberg series. In any experiment,

there is a ﬁnite resolution ∆ω with which the Rydberg

states can be excited. It can arise, for example, from the

Doppler width or a laser linewidth. This resolution de-

termines the cross section σ

for exciting the Rydberg

state of principal quantum number n. Explicitly, σ

given by

∆ω

(14.16)

A typical value for σ

is 10

−18

. For a resolu-

tion ∆ω = 1cm

−1

(6×10

−6

a.u.) the cross section for

exciting an n = 20 atom is 3× 10

−17

From the wave functions of the Rydberg states,

we can also derive the n

−3

dependence of the pho-

toexcitation cross section. The dipole matrix element

from the ground state to a Rydberg state only in-

volves the part of the Rydberg state wave function

near the core. At small r, the Rydberg wave func-

tion only depends on n through the n

−3

normalization

factor, and as a result, the squared dipole matrix

element between the ground state and the Ryd-

berg state and the cross section both have an n

−3

dependence.

Radiative decay, which is covered in Chapt. 17,is,

to some extent, the reverse of optical excitation. The

general expression for the spontaneous transition rate

from the n state to the n







state is the Einstein A

coefﬁcient, given by [14.2]

n,n







n,n







n,n







+ 1

(14.17)

Part B 14.2

238 Part B Atoms

where µ

n,n







and ω

n,n



,



are the electric dipole matrix

elements and frequencies of the n → n







transitions,

and g



are the degeneracies of the n and n







states,

and g

is the greater of g

and g



. The lifetime τ

n

the n state is obtained by summing the decay rates to

all possible lower energy states. Explicitly,

n









n,n







. (14.18)

Due to the ω

factor in (14.17), the highest frequency

transition usually contributes most heavily to the total

radiative decay rate, and the dominant decay is likely

to be the lowest lying state possible. For low- Rydberg

states, the lowest lying 



states are bound by orders of

magnitude more than the Rydberg states, and the fre-

quency of the decay is nearly independent of n. Only the

squared dipole moment depends on n,asn

−3

, because

of the normalization of the Rydberg wave function at the

core. Consequently, for low- states,

n

∝ n

. (14.19)

As a typical example, the 10f state in H has a lifetime

of 1.08 µs [14.7].

The highest  states, with  = n − 1, have radiative

lifetimes with a completely different n dependence. The

only possible transitions are n → n − 1, with frequency

1/n

. In this case the dipole moments reﬂect the large

size of both the n and n− 1 states and have the n

scaling

of the orbital radius. Using (14.17)for = n − 1 leads

n(n−1)

∝ n

. (14.20)

Another useful lifetime, τ

, is that corresponding to the

average decay rate of all , m states of the same n.It

scales as n

4.5

[14.2,8].

Equation (14.17) describes spontaneous decay to

lower lying states driven by the vacuum. At room tem-

perature, 300 K, there are many thermal photons at the

frequencies of the n → n± 1 transitions of Rydberg

states for n ≥ 10, and these photons drive transitions

to higher and lower states [14.9]. A convenient way of

describing blackbody radiation is in terms of the photon

occupation number

n,givenby

n =

ω/kT

− 1

(14.21)

The stimulated emission or absorption rate K

n,n







from

state n to state n







is given by

n,n







n,n







n,n







+ 1

(14.22)

Summing these rates over n



and 



gives the total

blackbody decay rate 1/τ

. Explicitly,

n









n,n







. (14.23)

The resulting lifetime τ

n

at any given temperature is

given by

n

= 1/τ

n

+ 1/τ

n

. (14.24)

For low- states with 10 < n < 20, blackbody radiation

produces a 10% decrease in the lifetimes, but for high-

states of the same n, it reduces the lifetimes by a factor of

ten. Since 1/τ

n

∝ n

−2

, this term must dominate normal

spontaneous emission at high n.

The above discussion of spontaneous and stimu-

lated transitions is based on the implicit assumption

that the atoms are in free space. If the atoms are in

a cavity, which introduces structure into the blackbody

and vacuum ﬁelds, the transition rates are signiﬁ-

cantly altered [14.10]. These alterations are described

in Chapt. 79. If the cavity is tuned to a resonance, it

increases the transition rate by the ﬁnesse of the cav-

ity (approximately the Q for low-order modes). On the

other hand, if the cavity is tuned between resonances,

the transition rate is suppressed by a similar factor.

14.3 Electric Fields

As a starting point, consider the H atom in a static electric

ﬁeld E in the z-direction, and focus on the states of

principal quantum number n. The ﬁeld couples  and

 ± 1 states of the same m bytheelectricdipolematrix

elements. Since the states all have a common zero ﬁeld

energy of −1/2n

, and the off-diagonal Hamiltonian

matrix elements are all proportional to E , the eigenstates

are ﬁeld-independent linear combinations of the zero

ﬁeld  states of the same m, and the energy shifts from

−1/2n

are linear in E . In this ﬁrst-order approximation,

the energies are given by [14.2]

E =−

− n

)nE , (14.25)

Part B 14.3

Rydberg Atoms 14.3 Electric Fields 239

where n

and n

are parabolic quantum numbers (see

Sect. 9.1.2) which satisfy

+ n

+|m|+1 = n . (14.26)

Consider the m = 0 states as an example. The n

− n

n − 1 state is shifted up in energy by

n(n − 1)E and is

called the extreme blue Stark state, and the n

− n

n − 1 state is shifted down in energy by

n(n − 1)E

and is called the extreme red Stark state. These two

states have large permanent dipole moments, and in the

red (blue) state the electron spends most of its time

on the downﬁeld (upﬁeld) side of the proton as shown

in Fig. 14.3, a plot of the potential along the z-axis.

We have here ignored the electric dipole couplings to

other n states, which introduce small second order Stark

shifts to lower energy. As implied by (14.26), states of

higher m have smaller shifts. In particular, the circular

m =  = n − 1 state has no ﬁrst order shift since there

are no degenerate states to which it is coupled by the

ﬁeld.

The Stark effect in other atoms is similar, but not

identical to that observed in H. This point is shown by

Fig. 14.4, a plot of the energies of the Na m = 0levels

near n = 20. The energy levels are similar to those of H

in that most of the levels exhibit apparently linear Stark

shifts from the zero ﬁeld energy of the high- states.

The differences, however, are twofold. First, the levels

from s and p states with nonzero quantum defects join

the manifold of Stark states at some nonzero ﬁeld, given

–250

–260

–270

–280

–290

–300

Energy (cm

–1

)

0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 2.0

ε (kV/cm)

n =19

n =20

22s

21p

21s

20p

Fig. 14.4 Energies of Na m = 0levelsofn ≈ 20 as a function of electric ﬁeld. The shaded region is above the classical

ionization limit

0.001

0.0

–0.001

–0.002

–0.003

–2800 –1600 0 1600 2800

z (a

)

E (arb. units)

Fig. 14.3 Combined Coulomb–Stark potential along the

z-axis when a ﬁeld of 5× 10

−7

a.u. (2700 V/cm) is ap-

pliedinthez-direction (solid). The extreme red state (R)

is near the saddlepoint, and the extreme blue (B) state

is held on the upﬁeld side of the atom by an effec-

tive potential (dashed) roughly analogous to a centrifugal

potential

Part B 14.3

240 Part B Atoms

approximately by [14.4]

E =

2δ





, (14.27)

where δ





is the magnitude of the difference between



and the nearest integer. Second, there are avoided

crossings between the blue n = 20 and red n = 21 Stark

states. In H these states would cross, but in Na they do

not because of the ﬁnite sized Na

core, which also

leads to the nonzero quantum defects of the nsandnp

states. This point, and other related points, are described

in Chapt. 15.

Field ionization is both intrinsically interesting

and of great practical importance for the detection of

Rydberg atoms [14.11]. The simplest picture of ﬁeld

ionization can be understood with the help of Fig. 14.4.

The potential along the z-axisofanatominaﬁeldE in

the z-direction is given by

V =−

− E z .

(14.28)

If an atom has an energy E relative to the zero ﬁeld limit,

it can ionize classically if the energy E lies above the sad-

dle point in the potential. The required ﬁeld is given by

E =

(14.29)

Ignoring the Stark shifts and using E =−1/2n

yields

the expression

E =

16n

. (14.30)

The H atom ionizes classically as described above,

or by quantum mechanical tunneling which occurs at

slightly lower ﬁelds. Since the tunneling rates increase

exponentially with ﬁeld strength, typically an order of

magnitude for a 3% change in the ﬁeld, specifying the

classical ionization ﬁeld is a good approximation to the

ﬁeld which gives an ionization rate of practical interest.

The red and blue states of H ionize at very different

ﬁelds, as shown by Fig. 14.5, a plot of the m = 0Stark

states out to the ﬁelds at which the ionization rates are

−1

[14.12]. First, note the crossing of the levels of

different n mentioned earlier. Second, note that the red

states ionize at lower ﬁelds than do the blue states, in

spite of the fact that they are lower in energy. In the

red states, the electron is close to the saddle point of the

potential of Fig. 14.3, and it ionizes according to (14.29).

If the Stark shift of the extreme red state to lower energy

is taken into account, (14.30) becomes

E =

. (14.31)

E (× 1000 cm

–1

)

–500

–1000

–1500

ε (kV/cm)

0 50 100

Fig. 14.5 Energies of H m = 0levelsofn = 9, 10, and 11

as functions of electric ﬁeld. The widths of the levels due

to ionization broaden exponentially with ﬁelds, and the

onset of the broadening indicated is at an ionization rate of

−1

.Thebroken line indicating the classical ionization

limit, E = E

/4 passes near the points at which the extreme

red states ionize

In the blue state the electron is held on the upﬁeld side

of the atom by an effective potential roughly analogous

to a centrifugal potential, as shown by Fig. 14.3.Atthe

same ﬁeld the blue state’s energy is lower relative to the

saddle point of its potential, shown by the broken line

of Fig. 14.3, than is the energy of the red state relative

to the saddle point of its potential, given by (14.28)and

shown by the solid line of Fig. 14.3. As shown by the

broken line of Fig. 14.5, the classical ionization limit of

(14.29) is simply a line connecting the ionization ﬁelds

of the extreme red Stark states. All other states are sta-

ble above the classical ionization limit. In the Na atom,

ionization of m = 0 states occurs in a qualitatively dif-

ferent fashion [14.12]. Due to the ﬁnite size of the Na

core, there are avoided crossings between the blue and

red Stark states of different n, as is shown by Fig. 14.4.

In the region above the classical ionization limit, shown

by the shaded region of Fig. 14.4, the same coupling

between hydrogenically stable blue states and the de-

generate red continua leads to autoionization of the blue

states [14.13]. As a result, all states above the classi-

cal ionization limit ionize at experimentally signiﬁcant

rates. In higher m states, the core coupling is smaller,

and the behavior is more similar to H.

Part B 14.3

Rydberg Atoms 14.4 Magnetic Fields 241

Field ionization is commonly used to detect Rydberg

atoms in a state selective manner. Experiments are most

often conducted at or near zero ﬁeld, and afterwards the

ﬁeld is increased in order to ionize the atoms. Exactly

howthe atoms pass from the low ﬁeld to the high ionizing

ﬁeld is quite important. The passage can be adiabatic,

diabatic or anything in between. The selectivity is best

if the passage is purely adiabatic or purely diabatic, for

in these two cases unique paths are followed.

In zero ﬁeld, optical excitation from a ground s state

leads only to ﬁnal np states. In the presence of an elec-

tric ﬁeld, all the Stark states are optically accessible,

because they all have some p character. The fact that

all the Stark states are optically accessible from the

ground state allows the population of arbitrary  states

of nonhydrogenic atoms by a technique called Stark

switching [14.6, 14]. In any atom other than H, the

 states are nondegenerate in zero ﬁeld, and each of

them is adiabatically connected to one, and only one,

high ﬁeld Stark state, as shown by Fig. 14.4. If one of

the Stark states is excited with a laser and the ﬁeld re-

duced to zero adiabatically, the atoms are left in a single

zero ﬁeld  state.

In zero ﬁeld, the photoionization cross section is

structureless. However, in an electric ﬁeld, it exhibits

obvious structure, sometimes termed strong ﬁeld mix-

ing resonances. Speciﬁcally, when ground state s atoms

are exposed to light polarized parallel to the static ﬁeld,

an oscillatory structure is observed in the cross section,

even above the zero ﬁeld ionization limit [14.15]. The

origin of the structure can be understood with the aid

of a simple classical picture [14.16, 17]. The electrons

ejected in the downﬁeld direction can simply leave the

atom, while the electrons ejected in the upﬁeld direc-

tion are reﬂected back across the ionic core and also

leave the atom in the downﬁeld direction. The wave

packets corresponding to these two classical trajecto-

ries are added, and they can interfere constructively or

destructively at the ionic core depending on the phase

accumulation of the reﬂected wave packet. Since the

phase depends on the energy, there is an oscillation in

the photoexcitation spectrum. This model suggests that

no oscillations should be observed for light polarized

perpendicular to the static ﬁeld, and none are. The os-

cillations can also be thought of as arising from the

remnants of quasistable extreme blue Stark states which

have been shifted above the ionization limit, and, using

this approach or a WKB approach, one can show that the

spacing between the oscillations at the zero ﬁeld limit is

∆E = E

3/4

[14.18,19].

The initial photoexcitation experiments were done

using narrow bandwidth lasers, so that the time de-

pendence of the classical pictures was not explicitly

observed. Using mode locked lasers it has been possible

to create a variety of Rydberg wave packets [14.20, 21]

and observe, in effect, the classical motion of an elec-

tron in an atom. Of particular interest, it has been

possible to directly observe the time delay of the ejec-

tion of electrons subsequent to excitation in an electric

ﬁeld [14.22].

14.4 Magnetic Fields

To ﬁrst order, the energy shift of a Rydberg atom due

to a magnetic ﬁeld B (the Zeeman effect) is propor-

tional to the angular momentum of the atom. Since the

states optically accessible from the ground state have

low angular momenta, the energy shifts are the same as

those of low-lying atomic states. In contrast, the sec-

ond order diamagnetic energy shifts are proportional to

the area of the Rydberg electron’s orbit and scale as

[14.23]. The diamagnetic interaction mixes the

 states, allowing all to be excited from the ground state,

and produces large shifts to higher energies. The energy

levels as a function of magnetic ﬁeld are reminiscent

of the Stark energy levels shown in Fig. 14.5, differing

in that the energy shifts are quadratic in the magnetic

ﬁeld.

One of the most striking phenomena in magnetic

ﬁelds is the existence of quasi-Landau resonances,

spaced by ∆E = 3

B/2, in the photoionization cross

section above the ionization limit [14.24]. The ori-

gin of this structure is similar to the origin of the

strong ﬁeld mixing resonances observed in electric

ﬁelds. An electron ejected in the plane perpendicu-

lar to the B ﬁelds is launched into a circular orbit

and returns to the ionic core. The returning wave

packet can be in or out of phase with the one

leaving the ionic core, and thus, can interfere con-

structively or destructively with it. While the electron

motioninthexy-plane is bound, motion in the

z-direction is unaffected by the magnetic ﬁeld and

is unbounded above the ionization limit, leading to

resonances of substantial width. The Coulomb poten-

tial does provide some binding in the z-direction and

allows the existence of quasistable three-dimensional

orbits [14.25].

Part B 14.4

242 Part B Atoms

14.5 Microwave Fields

Strong microwave ﬁelds have been used to drive mul-

tiphoton transitions between Rydberg states and to

ionize them. Here we restrict our attention to ion-

ization. Ionization by both linearly and circularly

polarized ﬁelds has been explored with both H and other

atoms.

Hydrogen atoms have been studied with linearly po-

larized ﬁelds of frequencies up to 36 GHz [14.26]. When

the microwave frequency ω  1/n

, ionization of m = 0

states occurs at a ﬁeld of E = 1/9n

/4),whichis

the ﬁeld at which the extreme red Stark state is ion-

ized by a static ﬁeld. Due to the second-order Stark

effect, the blue and red shifted states are not quite mir-

ror images of each other, and when the microwave ﬁeld

reverses, transitions between Stark states occur. There is

a rapid mixing of the Stark states of the same n and m by

a microwave ﬁeld, and all of them are ionized at the same

microwave ﬁeld amplitude, E = 1/9n

. Important points

are that no change in n occurs and the ionization ﬁeld is

the same as the static ﬁeld required for ionization of the

extreme red Stark state. As ω approaches 1/n

,theﬁeld

falls below 1/9n

due to ∆n transitions to higher lying

states, allowing ionization at lower ﬁelds. This form of

ionization can be well described as the transition to the

classically chaotic regime [14.27]. For ω>1/n

the ion-

ization ﬁeld is more or less constant, and for ω>1/2n

the process becomes photoionization.

The ionization of nonhydrogenic atoms by linearly

polarized ﬁelds has also been investigated at frequen-

cies of up to 30 GHz, but the result is very different

from the hydrogenic result. For ω  1/n

and low m,

ionization occurs at a ﬁeld of E ≈ 1/3n

[14.28]. This

is the ﬁeld at which the m = 0 extreme blue and

red Stark states of principal quantum number n and

n + 1 have their avoided crossing. For n = 20 this ﬁeld

is ≈ 500 V/cm, as shown by Fig. 14.4. How ioniza-

tion occurs can be understood with a simple model

based on a time-varying electric ﬁeld. As the mi-

crowave ﬁeld oscillates in time, atoms follow the Stark

states of Na shown in Fig. 14.4. Even with very small

ﬁeld amplitudes, transitions between the Stark states

of the same n are quite rapid because of the zero

ﬁeld avoided crossings. If the ﬁeld reaches 1/3n

,the

avoided crossing between the extreme red n and blue

n + 1 state is reached, and an atom in the blue n Stark

state can make a Landau–Zener transition to the red

n + 1 Stark state. Since the analogous red–blue avoided

crossings between higher lying states occur at lower

ﬁelds, once an atom has made the n → n + 1transi-

tion it rapidly makes a succession of transitions through

higher n states to a state which is itself ionized by the

ﬁeld.

The Landau–Zener description given above is some-

what oversimpliﬁed in that we have ignored the

coherence between ﬁeld cycles. When it is included,

we see that the transitions between levels are resonant

multiphoton transitions. While the resonant charac-

ter is obscured by the presence of many overlapping

resonances, the coherence substantially increases the

n → n + 1 transition probability even when E < 1/3n

The ﬁelds required for ionization calculated using this

model are lower than 1/3n

, in agreement with the ex-

perimental observations. Nonhydrogenic Na states of

high m behave like H, because no states with signiﬁ-

cant quantum defects are included, and the n → n + 1

avoided crossings are vanishingly small.

Experiments on ionization of alkali atoms by cir-

cularly polarized ﬁelds of frequency ω show that for

ω  1/n

, a ﬁeld amplitude of E = 1/16n

is required

for ionization [14.29]. This ﬁeld is the same as the static

ﬁeld required. In a frame rotating with frequency ω,

the circularly polarized ﬁeld is stationary and cannot

induce transitions, so this result is not surprising. On

the other hand, when the problem is transformed to

the rotating frame, the potential of (14.28) is replaced

V =−

− E x −

(14.32)

where ρ

= x

+ y

, and we have assumed the ﬁeld to

be in the x-direction in the rotating frame. This poten-

tial has a saddle point below E = 1/16n

[14.30]. As

n or ω is raised so that ω → 1/n

, the experimentally

observed ﬁeld falls below 1/16n

, but not so fast as im-

pliedby(14.32). Equation (14.32) is based solely on

energy considerations, and ionization at the threshold

ﬁeld implied by (14.32) requires that the electron es-

cape over the saddle point in the rotating frame at nearly

zero velocity. For this to happen, when ω approaches

1/n

, more than n units of angular momentum must be

transferred to the electron, which is unlikely. Models

based on a restriction of the angular momentum trans-

ferred from the ﬁeld to the Rydberg electron are in better

agreement with the experimental results. Small devia-

tions of a few percent from circular polarization allow

ionization at ﬁelds as low as E = 1/3n

. This sensitiv-

ity can be understood as follows. In the rotating frame,

a ﬁeld with slightly elliptical polarization appears to be

Part B 14.5

Rydberg Atoms 14.6 Collisions 243

a large static ﬁeld with a superimposed oscillating ﬁeld

at frequency 2ω. The oscillating ﬁeld drives transitions

to states of higher energy, allowing ionization at ﬁelds

less than E = 1/16n

In the regime in which ω>1/n

, microwave ion-

ization of nonhydrogenic atoms is essentially the same

as it is in H [14.31]. In this regime, the microwave

ﬁeld couples states differing in n by more than one,

and the pressure or absence of quantum defects is

not so important. Consequently, only for ω>1/n

is the microwave ionization of H and other atoms

different.

14.6 Collisions

Since Rydberg atoms are large, with geometric cross

sections proportional to n

, one might expect the cross

sections for collisions to be correspondingly large. In

fact, such is often not the case. A useful way of under-

standing collisions of neutral atoms and molecules with

Rydberg atoms is to imagine an atom or molecule M

passing through the electron cloud of an Na Rydberg

atom. There are three interactions

−

−Na

, e

−

−M , M−Na

. (14.33)

The long range e

−

–Na

interaction determines the en-

ergy levels of the Na atom. The short range of the

−

–M and M–Na

interactions makes it likely that

only one will be important at any given time. This

approximation, termed the binary encounter approxima-

tion, is described in Chapt. 56.TheM–Na

interaction

can only lead to cross sections of ≈ 10–100 Å

.On

the other hand, since the electron can be anywhere in

the cloud, the cross sections due to the e

−

–M interac-

tion can be as large as the geometric cross section of

the Rydberg atom. Accordingly, we focus on the e

−

–M

interaction.

Consider a thermal collision between M andanNa

Rydberg atom. Typically, M passes through the elec-

tron cloud slowly compared with the velocity of the

Rydberg electron, and it is the e

−

–M scattering which

determines what happens in the M–Na collision, as ﬁrst

pointed out by Fermi [14.32]. First consider the case

where M is an atom. There are no energetically acces-

sible states of atom M which can be excited by the low

energy electron, so the scattering must be elastic. The

electron can transfer very little kinetic energy to M,

but the direction of the electron’s motion can change.

With this thought in mind, we can see that only the

collisional mixing of nearly degenerate  states of the

same n has very large cross sections. The -mixing cross

sections are approximately geometric at low n [14.33].

If the M atom comes anywhere into the Rydberg or-

bit, scattering into a different  state occurs. At high n,

the cross section decreases, because the probability dis-

tribution of the Rydberg electron becomes too dilute,

and it becomes increasingly likely that the M atom

will pass through the Rydberg electron’s orbit with-

out encountering the electron. The n at which the peak

-mixing cross section occurs increases with the elec-

tron scattering length of the atom. While -mixing cross

sections are large, n changing cross sections are small



≈ 100 Å



since they cannot occur when the Rydberg

electron is anywhere close to the outer turning point of

its orbit [14.34].

If M is a molecule, there are likely to be energet-

ically accessible vibrational and rotational transitions

which can provide energy to or accept energy from

the Rydberg electron, and this possibility increases

the likelihood of n changing collisions with Rydberg

atoms [14.11]. Electronic energy from the Rydberg atom

must be resonantly transferred to rotation or vibration

in the molecule. In heavy or complex molecules, the

presence of many rotational-vibrational states tends to

obscure the resonant character of the transfer, but in sev-

eral light systems the collisional resonances have been

observed clearly [14.11].

Using the large Stark shifts of Rydberg atoms it

is possible to tune the levels so that resonant energy

transfer between two colliding atoms can occur [14.35]

by the resonant dipole–dipole coupling,

Vd =

. (14.34)

Here µ

and µ

are the dipole matrix elements of the

upward and downward transitions in the two atoms, and

R is their separation. At room temperature, this process

leads to enormous cross sections, substantially in excess

of the geometric cross sections. At the low temperatures

(300 µK) attainable using cold atoms, the atoms do not

move, and therefore cannot collide. However, resonant

dipole–dipole energy transfer is still observed due to the

static dipole–dipole interactions of not two, but many

atoms [14.36,37].

Part B 14.6