Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics
Подождите немного. Документ загружается.


224 Part B Atoms
12.3 Diagonal Representation: State Populations
An ensemble is said to be in a coherent state when
one or more of the off-diagonal elements of the density
matrix do not vanish. In a manifold of angular momen-
tum substates of a single total angular momentum j,
the ensemble has coherence if and only if it is not axi-
ally symmetric, that is, if and only if [ρ, J
z
] = 0. In an
ensemble lacking coherence, or one in which any coher-
ence that is present does not affect the observation, only
the N = 2 j +1 diagonal elements of the N × N density
matrix, those that represent state populations, need be
considered. In terms of multipoles, only the N elements
ρ
L0
then play a role; the ρ
LM
elements with M = 0
can be safely ignored. Such a diagonal representation is
valid whenever (1) the time evolution of the system is
axially symmetric and (2) either the preparation of the
system or its detection is axially symmetric.
12.4 Interaction with Light
A polarized system can be prepared in a variety of ways,
including beam splitting in external fields, collisional
excitation (including beam-foil excitation of fast beams),
or radiative excitation with directed and/or polarized
light. Several options for the detection of multipoles
also exist, including the measurement of the anisotropy
and/or polarization of scattered particles or photons. In
this section, the interaction of the atomic ensemble with
dipole radiation is considered.
It is convenient to define a detection operator for
electric dipole radiation of polarization
ˆ
by
D
λ
ˆ
=
µ
ˆ
· d
|
λµ
λµ
|
d·
ˆ
∗
(12.20)
for decay to the state λ. Here, d =
k
er
k
is the dipole-
moment operator of the atom and µ is a magnetic
sublevel of λ. The detection operator is a vector in
Liouville space and can be expanded in irreducible
tensor operators according to
D
λ
ˆ
=
LM
D
λLM
ˆ
T
LM
,
(12.21)
where
D
λLM
ˆ
= T
∗
LM
· D
λ
ˆ
= B
L
(
λ
)
Φ
LM
ˆ
,
(12.22)
with the dynamics contained in
B
L
(
λ
)
=
(
−1
)
λ+L+j+1
d
jλ
2
1 L 1
j λ j
,
(12.23)
and the angular dependence in
Φ
LM
ˆ
=
(
2L +1
)
1/2
rs
ˆ
·
ˆ
r
ˆ
·
ˆ
s
∗
×
(
−1
)
1−s
1 L 1
r λ −s
.
(12.24)
Here,
ˆ
r and
ˆ
s range over the unit spherical tensors of
rank one, namely ±
ˆ
1 =∓
ˆ
x±i
ˆ
y
/
√
2and
ˆ
0 =
ˆ
z (see
also Omont [12.6], who gives tables of Φ
LM
), and d
jλ
is a reduced matrix element of d.
The intensity of radiation of polarization
ˆ
emit-
ted by an excited ensemble of atoms with state
density matrix ρ in its radiative decay to level λ
is
ρ
∗
·D
λ
ˆ
=
m,n,µ
λµ
|
d·
ˆ
∗
|
m
ρ
mn
n
|
d·
ˆ
|
λµ
=
LM
ρ
LM
D
λLM
,
(12.25)
and by selection of polarization or spatial distribu-
tion, individual multipole components D
λLM
and hence
ρ
LM
can be determined. The source terms S
LM
ex-
cited by electric-dipole radiation from an isotropic
ground state are given by a linear combination of
D
λLM
:
S
LM
=
(
2π
)
2
λ,
ˆ
u
ˆ
(
λ
)
D
λLM
ˆ
,
(12.26)
where u
ˆ
(λ) is the energy density of exciting ra-
diation with polarization vector
ˆ
per unit energy.
From the 3 − j symbol in (12.24), only the L = 0, 1,
and 2 components of ρ are observable unless the
splitting of the Zeeman sublevels of λ are spec-
troscopically resolved. Similarly, if the ground state
is unpolarized and its Zeeman sublevels unresolved,
then only L = 0, 1, and 2 components of ρ can
be excited. To excite higher-order multipoles, the
ground state can be polarized by optical pump-
ing [12.7].
As an example, consider the axially symmetric sys-
tem discussed in Sect. 12.1 with j = 3/2 in the excited
state and λ = 1/2 in the ground state. Only the four
Part B 12.4

Atomic Multipoles 12.5 Extensions 225
diagonal elements of D(
ˆ
),
D
m
ˆ
=
µ
jm
ˆ
· d
λµ
2
=
d
jλ
2
µr
ˆ
·
ˆ
r
2
λ 1 j
−µ rm
2
,
are needed for the 2 j +1valuesofm =−j,... , j,
where µ ranges over the 2λ +1 values from −λ to λ
and r =±1, 0. One finds directly
D
ˆ
=
d
jλ
2
12
ˆ
· −
ˆ
1
2
3
1
0
0
+
ˆ
·
ˆ
0
2
0
2
2
0
+
ˆ
·
ˆ
1
2
0
0
1
3
.
(12.27)
The detected signal of polarization
ˆ
is proportional
to N· D(
ˆ
),whereN is the population–density vector
(12.1). Some of the state polarization can be monitored
by looking at polarized dipole radiation. If the emitted
light is observed as it propagates perpendicular to the
polarization vector, the intensities are given to within an
overall constant of proportionality by
I
σ±
= D
"
±
ˆ
1
#
· N, I
π
= D
"
ˆ
0
#
· N ,
(12.28)
I
σ
= D
"
ˆ
ξ
#
· N =
1
2
(
I
σ+
+I
σ−
)
,
(12.29)
where
ˆ
ξ is any real unit vector (linear polarization vector)
in the xy-plane. The intensities of polarized radiation
may also be given in terms of Stokes parameters [12.8]
(see also Chapt. 7). By expanding N in the spherical
basis vectors T
L
as in (12.5), one obtains a detected
signal
N· D
ˆ
=
2 j+1
L=0
n
L
D
λL0
(12.30)
=
d
jλ
2
12
$
2n
0
+
√
5
%
ˆ
·
ˆ
1
2
−
ˆ
· −
ˆ
1
2
&
n
1
+
%
3
ˆ
·
ˆ
0
2
−1
&
n
2
'
.
(12.31)
Thus there is no way to monitor the octupole polarization
n
3
from the dipole radiation since D
λLM
=0forL > 2.
To monitor the orientation n
1
, the circular polarization
must be measured
√
5
3
n
1
n
0
=
I
σ+
−I
σ−
2I
σ
+I
π
, (12.32)
since the coefficient D
λL0
vanishes for any linear polar-
ization. Conversely, from
n
2
2n
0
=
I
σ
−I
π
2I
σ
+I
π
, (12.33)
alignment is given by linear polarization. However, the
denominator in both cases is different from that com-
mon in polarization measurements, and indeed, the ratio
(I
σ+
−I
σ−
)/(I
σ+
+I
σ−
) is not proportional to the ori-
entation but contains a contribution from the alignment,
and (I
σ
−I
π
)/(I
σ
+I
π
) is not linear in the alignment.
The expressions for other total angular momenta j are
the same except for the numerical coefficients on the
LHS of (12.32)and(12.33). Finally, if the desire is to
measure the total excited-state population n
0
without
any polarization component (which might rotate in stray
external fields), one can choose linear polarization at an
angle to make D
λ20
disappear, namely at the “magic an-
gle” θ = arccos 3
−1/2
= 54.74 degrees. Of course, the
same angle may be chosen to excite an unpolarized
population.
12.5 Extensions
Although the discussion here has focused on cell experi-
ments in which collisional perturbations are isotropic
and state manifolds with a given total angular momen-
tum j are well isolated, the concept of state multipoles
is also useful in many applications where the collision
symmetry is lower and where states with different j
values interact, possibly due to the presence of fine
and hyperfine structure [12.1]. Applications have been
made in electron–atom collisions (Chapt. 7), atom–atom
collisions [12.9], and atom–molecule collisions [12.5].
Part B 12.5

226 Part B Atoms
References
12.1 W. E. Baylis: Part. B, Chap. 28. In: Progress in
Atomic Physics, ed. by W. Hanle, H. Kleinpoppen
(Plenum, New York 1977)
12.2 U. Fano: Rev. Mod. Phys. 29, 74 (1957)
12.3 U.Fano,G.Racah:Irreducible Tensorial Sets (Aca-
demic, New York 1967)
12.4 E. L. Lewis: Phys. Rep. 58,1(1980)
12.5 W. E. Baylis, J. Pascale, F. Rossi: Phys. Rev. A 36,
4212 (1987)
12.6 A. Omont: Prog. Quantum Electron. 5, 69 (1977)
12.7 W. Happer: Rev. Mod. Phys. 44,169(1972)
12.8 W. E. Baylis, J. Bonenfant, J. Derbyshire, J. Huschilt:
Am. J. Phys. 61, 534 (1993)
12.9 E. E. Nikitin, S. Ya. Umanski: Theory of Slow Atomic
Collisions (Springer, Berlin, Heidelberg 1984)
Part B 12
227
Atoms in Stron
13. Atoms in Strong Fields
Interest in the effect that electric and magnetic
fields have on the internal structure of atoms is
as old as quantum mechanics itself. In practical
terms, an atom’s spectrum acts as its signature,
and so it is important to understand how elec-
tric and magnetic fields alter this characteristic. In
this chapter, a summary of the basic nonrelativis-
tic and relativistic theory of electrons and atoms
in external magnetic fields is given. Extensions to
thecaseofverystrongfieldsarethenintroduced
for both types of fields.
13.1 Electron in a Uniform Magnetic Field..... 227
13.1.1 Nonrelativistic Theory ................ 227
13.1.2 Relativistic Theory ..................... 228
13.2 Atoms in Uniform Magnetic Fields ......... 228
13.2.1 Anomalous Zeeman Effect .......... 228
13.2.2 Normal Zeeman Effect................ 229
13.2.3 Paschen–Back Effect.................. 229
13.3 Atoms in Very Strong Magnetic Fields .... 230
13.4 Atoms in Electric Fields ........................ 231
13.4.1 Stark Ionization ........................ 231
13.4.2 Linear Stark Effect ..................... 231
13.4.3 Quadratic Stark Effect ................ 232
13.4.4 Other Stark Corrections............... 232
13.5 Recent Developments........................... 233
References .................................................. 234
13.1 Electron in a Uniform Magnetic Field
13.1.1 Nonrelativistic Theory
The nonrelativistic Hamiltonian (in Gaussian units) for
an electron in an external field A is [13.1]
H =
1
2m
p−
e
c
A
2
−µ · B+eV , (13.1)
where A is the vector potential and V is the scalar po-
tential. The second term in (13.1) must be included to
account for the interaction of the electron magnetic mo-
ment with an external magnetic field. The potentials A
and V are only defined to within a gauge transforma-
tion [13.2]:
A
= A+∇f , V
= V −
1
c
∂ f
∂t
.
(13.2)
We choose the gauge ∇· A= 0 in which the momentum
operator p = i
∇ and vector potential A commute. B is
a constant uniform magnetic field with vector potential
A=
1
2
B× r .
(13.3)
µ is the magnetic moment of the electron:
µ =
1
2
g
e
µ
B
σ , (13.4)
where the σ
i
are the Pauli spin matrices, µ
B
= e /2m
e
c
is the Bohr magneton and g
e
is the electron g-factor
which accounts for the anomalous magnetic moment of
the electron (see Sect. 27.4).
Consider now the case of a free electron in a constant
uniform field in the z-direction with no scalar potential,
i. e., V = 0in(13.1). This case also describes an atom in
the limit of strong magnetic fields such that the Coulomb
interactions are negligible. In this case, which is different
from (13.3), we have
B = B
ˆ
z with
A
x
=−By
A
y
= A
x
= 0
.
(13.5)
For this field, the operators µ
z
, p
x
and p
z
commute with
the Hamiltonian and are therefore conserved. Calling
their respective eigenvalues µ
z
, p
x
and p
z
, with −∞ ≤
p
x
, p
y
≤∞, the eigenstates are written as
ψ = e
i
p
x
x+p
z
z
/
ϕ(y). (13.6)
Calling y
0
=−cp
x
/eB, ϕ satisfies
−
2
2m
d
2
dy
2
ϕ +
1
2
mω
2
B
(
y− y
0
)
2
ϕ
=
E +µ
z
B−
p
2
z
2m
ϕ,
(13.7)
Part B 13
228 Part B Atoms
which is the Schrödinger equation for a one-
dimensional harmonic oscillator with angular frequency
ω
B
=|e|B/mc, the cyclotron frequency of the electron.
The solutions to (13.7) give the eigenstates for an elec-
tron in an external homogeneous magnetic field. They
are called Landau levels [13.1] with energies given
by
E
n
=
n +
1
2
+m
s
ω
B
+
p
2
z
2m
,
(13.8)
where m
s
=± /2 is the eigenvalue of the z-component
of the spin operator s, and eigenfunctions given
by
ϕ
n
(y) =
1
π
1/2
a
B
2
n
n!
×exp
−
(y− y
0
)
2
2a
2
B
H
n
y− y
0
a
B
,
(13.9)
where a
B
=
√
/mω
B
and the H
n
are Hermite polyno-
mials [13.3].
13.1.2 Relativistic Theory
The relativistic analog of (13.1) is given by the Dirac
Hamiltonian
H
D
= cα ·
p−
e
c
A
+βmc
2
+eV , (13.10)
where α and β are the 4 × 4 matrices defined by (9.61).
The eigenfunctions of the Dirac Hamiltonian (13.10)are
written as four-dimensional spinors:
ψ
D
=
ψ
(1)
ψ
(2)
ψ
(3)
ψ
(4)
≡
φ
1
φ
−1
χ
1
χ
−1
≡
φ
χ
,
(13.11)
where φ and χ are two-dimensional (Pauli) spinors and
φ
i
and χ
i
are functions of the coordinates of the electron.
In the case V = 0, the lower component χ can
be eliminated in the eigenvalue equation H
D
ψ = Eψ
to obtain a Hamiltonian equation for φ only, sim-
ilar to (13.1) [13.4]. For a field defined by (13.5)
one writes φ in the form (as in the nonrelativistic
case)
φ = e
i( p
x
x+p
z
z)/
f(y). (13.12)
Here, f(y) satisfies the equation
−
2
2m
d
2
dy
2
ϕ +
1
2
mω
2
B
(
y− y
0
)
2
ϕ
=
E
2
−m
2
c
4
2mc
2
+µ
z
B−
p
2
z
2m
ϕ,
(13.13)
which reduces to the nonrelativistic form (13.7)inthe
limit E → mc
2
.In(13.13), the term involving µ is not
included arbitrarily as in (13.1) but is a consequence
of H
D
φ, which predicts the value g = 2. The value g
e
used in (13.4) includes radiative corrections to the Dirac
value.
From (13.13) we obtain
E
2
n
= 2mc
2
mc
2
2
+
n +
1
2
+m
s
ω
B
+
p
2
z
2m
,
(13.14)
and the eigenfunctions ψ
D
m
s
are
ψ
D
1/2
= N
E +mc
2
c
ψ
n
0
p
z
ψ
n
−
i
a
B
√
2n ψ
n−1
,
ψ
D
−1/2
= N
0
E +mc
2
c
ψ
n
i
a
B
2(n+1)ψ
n+1
−p
z
ψ
n
,
(13.15)
where ψ
n
is defined as in (13.6)and(13.9), and N is
a normalization constant.
13.2 Atoms in Uniform Magnetic Fields
13.2.1 Anomalous Zeeman Effect
Consider now the nonrelativistic Hamiltonian for a one-
electron atom in the presence of an external magnetic
field B. The one-electron Hamiltonian can be written
as [13.5]
H =
1
2m
p
2
−
1
4π
0
Ze
2
r
+ξ(r)L·S
+
µ
B
(
L+g
e
S
)
· B+
e
2
8mc
2
(B× r)
2
, (13.16)
Part B 13.2
Atoms in Strong Fields 13.2 Atoms in Uniform Magnetic Fields 229
where
ξ(r) =
1
2m
2
c
2
Ze
2
4π
0
1
r
3
. (13.17)
The anomalous Zeeman effect corresponds to the
case of weak magnetic fields such that the magnetic
interaction is small compared with the L·S spin-orbit
term. The energy shifts are obtained from a pertur-
bation of (13.16) with B = 0. The unperturbed wave
functions are eigenfunctions of L
2
, S
2
, J
2
and J
z
, with
J = L+S, but are not eigenfunctions of L
z
or S
z
.The
energy levels with given values of l, s and j split in
the presence of a field defined by (13.5) according
to
∆E
m
j
= gµ
B
Bm
j
, (13.18)
where g is the Land
´
e splitting factor given by
g = g
l
j( j +1) −s(s+1) +l(l+1)
2 j( j +1)
+g
e
j( j +1) +s(s+1) −l(l+1)
2 j( j +1)
,
(13.19)
where g
e
is defined by (13.4), and g
l
= 1 −m
e
/M to
lowest order in m
e
/M,wherem
e
is the electron mass
and M is the nuclear mass. To a first approximation, it
is often sufficient to take g
e
= 2 (the Dirac value) and
g
l
= 1. In the case of a many-electron atom, j, l and s
are replaced by the total angular momenta J, L and S.In
the one-electron case (neglecting corrections to g
l
or g
e
)
the g-value is simply
g ≈
j +
1
2
l+
1
2
, (13.20)
which shows that the splitting of the j = l+
1
2
levels
is larger than that of the j = l−
1
2
levels. The selec-
tion rules for the splitting of spectral lines are δm
j
= 0
for components polarized parallel to the field (π com-
ponents), and δm
j
=±1 for those perpendicular to the
field (σ components).
13.2.2 Normal Zeeman Effect
For moderately strong fields up to B ∼ 10
4
T, the quad-
ratic (B× r )
2
term in (13.16) can be neglected. If the
spin-orbit interaction term is also neglected, then the en-
ergies relative to the field-free eigenvalues E
n
are given
by
E
n
(B) = E
n
+µ
B
B(m
l
+2m
s
). (13.21)
The selection rules for transitions are ∆m
s
= 0and
∆m
l
= 0, ±1. The transition energy of a spectral line
is split into three components, the Lorentz triplet
∆E
n
= ∆E
n,0
+(∆m
l
) ω
L
, (13.22)
where ∆E
n,0
is the transition energy in the absence
of a field, and ω
L
=|e|B/2m is the Larmor frequency.
Transitions with ∆m
l
= 0 produce the π line at the
unshifted transition energy; transitions with ∆m
l
=±1
produce the shifted σ lines. Lorentz triplets can be ob-
served in many-electron atoms in which the total spin is
zero.
13.2.3 Paschen–Back Effect
We add now to the results of the last section the first-
order perturbation caused by the spin-orbit term. The
calculation can be performed in closed form for hydro-
genic atoms, for which the contribution to the energy of
the level n is [13.6]
∆E
n
= 0 , for l = 0
∆E
n
=
α
4
Z
4
µc
2
2n
3
m
l
m
s
×
l
l+
1
2
(l+1)
, for l = 0
(13.23)
where µ is the reduced mass, µ = mM/(m +M).
A general expression of the relativistic solution for the
Paschen–Back effect can be written for the one-electron
case in the Pauli approximation in which the eigenstates
are given in terms of φ in (13.11). Call φ
0
±
the eigenfunc-
tions with no external field corresponding to j = l±
1
2
with unperturbed energies E
0
±
respectively. In terms of
the dimensionless variables
η =
µ
B
B
E
+
− E
−
,=
1 +η
4m
j
2l+1
+η
2
,
γ =
1
1 +η
4m
j
2l+1
,
(13.24)
the energies E
±
and wave functions φ
±
of the states, in
the presence of the field B,are
E
±
=
E
0
+
2
(1 ± +2m
j
η) +
E
0
−
2
(1 ∓ −2m
j
η)
(13.25)
and
φ
±
=±
1 ±γ
2
φ
0
+
+
1 ∓γ
2
φ
0
−
. (13.26)
Part B 13.2

230 Part B Atoms
13.3 Atoms in Very Strong Magnetic Fields
The case of very strong magnetic fields (i. e., B > 10
4
T),
such as those encountered at the surface of neutron stars,
is also called the quadratic Zeeman effect,asthelast
term in (13.16) is dominant. In this range, perturbation
calculations fail to yield good results as the field is too
large, and even at fields of the order B ∼ 10
7
Tthe
Landau high B approximation of (13.8)and(13.9)is
not adequate.
Very accurate calculations have been performed us-
ing variational finite basis set techniques for both the
relativistic Dirac and nonrelativistic Schrödinger Hamil-
tonians. The calculations use the following relativistic
basis set [13.7] that includes nuclear size effects (R is
the nuclear size) and contains both asymptotic limits,
the Coulomb limit for B = 0 and the Landau limit for
B →∞:
ψ
(k,ν)
nl
=
r
q
k
−1+2n
e
−a
(k)
nν
r
2
−βρ
2
Ω
k
r ≤ R
b
(k)
nν
r
γ
ν
−1+n
e
−λr−βρ
2
Ω
k
r > R
(13.27)
with
Ω
k
= (cos θ)
l−|m
k
|
(sin θ)
|m
k
|
e
im
k
φ
ω
k
, (13.28)
where
n = 0, 1,... ,N
r
, k =1, 2, 3, 4,ν= 1, 2, 3, 4 ,
q
1
= q
2
= k
0
, q
3
= q
4
= k
0
,
m
k
= µ −σ
k
/2,σ
1
= σ
3
= 1,σ
2
= σ
4
=−1 .
Here, k refers to the component ψ
(k)
in (13.11), and λ
and β are variational parameters. The power of r at the
origin is given by
k
0
=
|κ| if κ<0
|κ|+1ifκ>0 ,
(13.29)
k
0
=
|κ|+1ifκ<0
|κ| if κ>0 ,
(13.30)
The index ν refers to the two regular and two irregular
solutions for r > R that match the corresponding powers
at the origin k
0
and k
0
.
γ
1
= γ
0
,γ
2
= γ
0
+1,γ
3
=−γ
0
,γ
4
=−γ
0
+1 ,
(13.31)
γ
0
=
κ
2
−(αZ)
2
,κ=∓
ν ±
1
2
+
1
2
,
(13.32)
ω
1
=
ϑ
1
0
,ω
2
=
ϑ
−1
0
,
ω
3
=
0
iϑ
−1
,ω
4
=
0
iϑ
−1
,
(13.33)
where ϑ
k
is a two-component Pauli spinor: σ
z
ϑ
k
= kϑ
i
.
For even (odd) parity states, the value of l for the large
components (k = 1, 2) is an even (odd) number greater
than or equal to |m
k
| up to 2N
θ
(for even parity) or
2N
θ
+1 (for odd parity), while for the small compo-
nents (k =3, 4) it is an odd (even) number greater than
or equal to |m
k
| up to 2N
θ
+1 (for even parity) or 2N
θ
(for odd parity), since the small component has a dif-
ferent nonrelativistic parity than the large component.
The coefficients a
(k)
nν
and b
(k)
nν
are determined by the
continuity condition of the basis functions and their first
derivatives at R. For a point nucleus, the section r ≤ R
is omitted; for a nonrelativistic calculation, take α = 0
in the basis set.
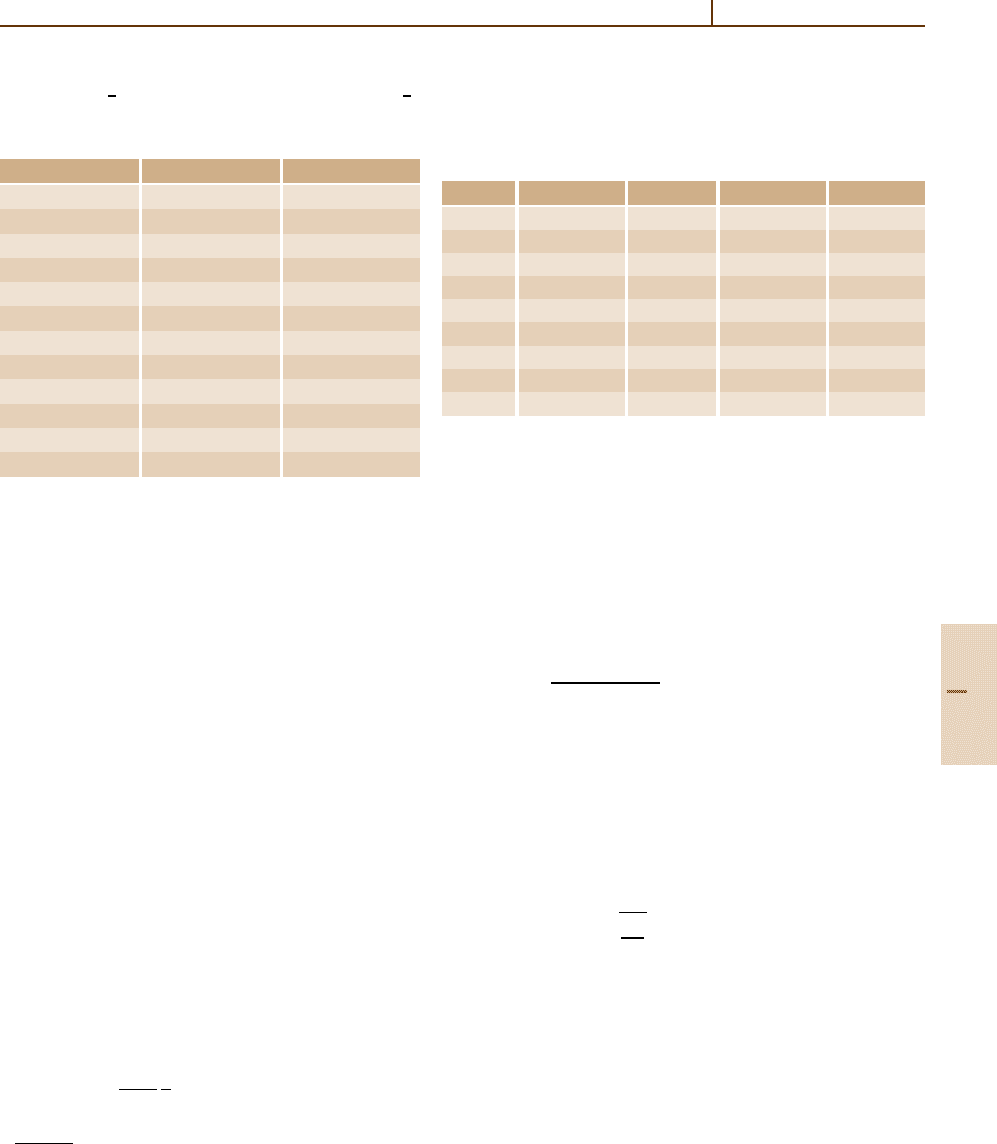
Table 13.1 presents relativistic (Dirac) energies for
the ground state of one-electron atoms. Values for a point
nucleus and finite nuclear size corrections are given.
Table 13.2 presents the relativistic energies for n = 2
Table 13.1 Relativistic ground state binding energy
−E
gs
/Z
2
and finite nuclear size correction δE
nuc
/Z
2
(in
a.u.) of hydrogenic atoms for various magnetic fields B (in
units of 2.35 × 10
5
T). δE
nuc
should be added to E
gs
Z B −E
gs
/Z
2
δE
nuc
/Z
2
1 0 0.500 006 656 597 483 75 1.557 86 × 10
−10
1 10
−5
0.500 011 656 4837 1.5579 × 10
−10
1 10
−2
0.504 981 572 360 1.5580 × 10
−10
1 10
−1
0.547 532 408 3429 1.5718 × 10
−10
1 2 1.022 218 0290 3.23 × 10
−10
1 10 1.747 800 68 1.182 × 10
−9
1 20 2.215 400 91 2.360 × 10
−9
1 200 4.727 1233 3.032 × 10
−8
1 500 6.257 0326 8.778 × 10
−8
20 0 0.502 691 308 407 5098 1.3372 × 10
−6
20 1 0.503 930 867 05 1.34 × 10
−6
20 10 0.514 950 248 1.3×10
−6
20 100 0.612 377 94 1.4×10
−6
40 0 0.511 129 686 143 1.1878× 10
−5
92 0 0.574 338 140 7377 8.4155 × 10
−4
92 1 0.574 386 987 8.4155 × 10
−4
Part B 13.3
Atoms in Strong Fields 13.4 Atoms in Electric Fields 231
Table 13.2 Relativistic binding energy −E
2S,−1/2
for the
2S
1/2
m
j
=−
1
2
and −E
2P,−1/2
for the 2P
1/2
m
j
=−
1
2
excited states of hydrogen (in a.u.) in an intense magnetic
field B (in units of 2.35 × 10
5
T)
B −E
2S,−1/2
−E
2P,−1/2
10
−6
0.125 002 580 164 0.125 002 283 074
10
−5
0.125 006 104 950
10
−4
0.125 052 044 95 0.125 050 967 92
10
−3
0.125 499 4694
10
−2
0.129 653 6428 0.129 851 3642
0.05 0.142 018 956
0.1 0.148 091 7386 0.162 411 0524
0.2 0.148 989 58
0.5 0.150 810 15
1 0.160 471 07 0.260 009 34
10 0.208 955 91 0.382 663 18
100 0.256 191 0.463 6641
excited states of hydrogen with the (negligible) finite
nuclear size correction included.
Table 13.3 Relativistic corrections δE = (E − E
NR
)/|E
R
|
to the nonrelativistic energies E
NR
for the ground state and
n = 2 excited states of hydrogen in an intense magnetic field
B (in units of 2.35 × 10
5
T). The numbers in brackets denote
powers of 10
B δE
gs
B δE
2S,−1/2
δE
2P,−1/2
0.1 −1.08[−5] 1[−6] −1.66[−5] −1.43[−5]
1 −5.21[−6] 1[−4] −1.66[−5] −7.86[−6]
2 −4.03[−6] 1[−3] −7.72[−6]
3 −3.48[−6] 1[−2] −1.60[−5] −7.30[−6]
20 −1.09[−6] 0.05 −1.57[−5]
200 4.61[−6] 0.1 −1.74[−6] −6.00[−6]
500 8.81[−6] 1 −1.3[−5] −1.05[−5]
2000 1.85[−5] 10 −2.0[−5] −3.48[−5]
5000 2.78[−5] 100 −3.9[−5] −1.0[−4]
Table 13.3, which displays the relativistic correc-
tions of the energies of the previous two tables, presents
one of the most interesting relativistic results: the change
in sign of the relativistic correction of the energy of the
ground state at B ∼ 10
7
T.
13.4 Atoms in Electric Fields
13.4.1 Stark Ionization
An external electric field F introduces the perturbing
potential
V =−d· F ,
(13.34)
where
d =
i
q
i
r
i
(13.35)
is the dipole moment of the atom, and i runs over all
electrons in the atom. In the case of strong external
electric fields, bound states do not exist because the
atom ionizes. Consider a hydrogenic atom in a static
electric field
F = F
ˆ
z .
(13.36)
The total potential acting on the electron is then
V
tot
(r) =−
e
2
Z
4π
0
1
r
+eFz .
(13.37)
Consider the z-dependence of this potential. Call ρ =
x
2
+y
2
and v(z,ρ)= V(x, y, z). Unlike the Coulomb
case in which v
Coul
(±∞,ρ)= 0 resulting in an infinite
number of bound states, now v(±∞,ρ)=±∞and v has
a local maximum. On the z axis, this maximum occurs
at z
max
=−
√
Z|e|/(4π
0
F) for which v(z
max
, 0) =0.
There is then a potential barrier through which the elec-
tron can tunnel, i. e., there are no bound states any longer
but resonances. The potential barrier is shallower the
stronger the field; the well can contain a smaller number
of bound states and ionization occurs.
13.4.2 Linear Stark Effect
The electric field (13.36) produces a dipole potential
V
F
= eFz = eFr
4π
3
Y
10
(
ˆ
r), (13.38)
which does not preserve parity. A first-order perturbation
calculation for the energy
E
(1)
n
=
n
|
V
F
|
n
(13.39)
yields null results unless the unperturbed states are
degenerate with states of opposite parity.
In the remainder of this chapter, atomic units will
be used. Final results for energies can be multiplied by
2R
∞
hc to translate to SI or other units. The calculation
can be carried out in detail for the case of hydrogenic
Part B 13.4

232 Part B Atoms
atoms [13.8]. In this case it is convenient to work in
parabolic coordinates: ϕ denotes the usual angle in the
xy-plane, and
ξ =r +z ,
η =r −z .
(13.40)
The Hamiltonian for a hydrogenic atom with a field
V
F
=
1
2
F (ξ −η) from (13.38)is
(ξ +η)H = ξh
+
(ξ) +ηh
−
(η) . (13.41)
The wave function is written in the form
Ψ(ξ, η, ϕ) =
1
√
2πZ
ψ
+
(ξ)ψ
−
(η)e
im
l
ϕ
, (13.42)
with the ψ
±
satisfying
h
±
(x)ψ
±
(x) = Eψ
±
(x), (13.43)
where x = ξ for ψ
+
and x = η for ψ
−
,and
h
±
(x) =−
2
x
d
dx
x
d
dx
−
2Z
±
x
+
m
2
l
2x
2
∓
1
2
Fx ,
(13.44)
with
Z = Z
+
+ Z
−
. (13.45)
Using the notation
=
√
−2E ,
n
±
= Z
±
/ −
1
2
(|m
l
|+1),
n = n
+
+n
−
+|m
l
|+1 ,
n
+
, N
−
= 0, 1,... ,n−|m
l
|+1 ,
|m
l
|=0, 1, 2,... ,n −1 ,
δn = n
+
−n
−
, (13.46)
where n is the principal quantum number, the unper-
turbed eigenfunctions are
ψ
±
(x) =
n
±
!
1
2
(n
±
+|m
l
|)!
1
2
e
−
1
2
x
(x )
1
2
|m
l
|
L
(|m
l
|)
n
±
(x ),
(13.47)
where the L
(a)
b
are generalized Laguerre polynomials
(Sect. 9.4.2). The zero-order eigenvalues are
Z
(0)
±
=
n
±
+
m
l
+1
2
.
(13.48)
The first-order perturbation yields
Z
(1)
±
=±
1
4
F
2
6n±(n
±
+m
l
+1) +m
l
(m
l
+3) +2
. (13.49)
From these
=
Z
n
−
3
2 F
n
Z
2
δ
n
, (13.50)
and to first order in F,
E =−
1
2
2
≈ E
(0)
+ E
(1)
,
E
(0)
=−
1
2
Z
2
n
2
,
E
(1)
=
3
2
F
Z
n δ
n
. (13.51)
13.4.3 Quadratic Stark Effect
A perturbation linear in the field F yields no contri-
bution to nondegenerate states (e.g., the ground state
n
+
= n
−
= m = 0; n =1). In this case, the lowest order
contribution comes from the quadratic Stark effect,the
contribution of order F
2
. The quadratic perturbation to
alevelE
(0)
n
caused by a general electric field F can be
written in terms of the symmetric tensor α
n
ij
as
E
(2)
n
=−
1
2
α
n
ij
F
i
F
j
, (13.52)
with
α
n
ij
=−2
m
m=n
n
|
d
i
|
m
m
d
j
n
E
n
− E
m
, (13.53)
where d
i
is defined in (13.35).
For a field (13.36),
∆E
n
=−
1
2
α
n
F
2
, (13.54)
where
α
n
≡ α
n
zz
=−2e
2
m
m=n
|
n
|
z
|
m
|
2
E
n
− E
m
. (13.55)
In terms of (13.46), a general nonrelativistic expression
for the dipole polarizability of hydrogenic ions is [13.9]
α
n
=
a
3
0
n
4
8Z
4
17n
2
−3 δ
2
n
−9m
2
l
+19
. (13.56)
For the ground state of hydrogenic atoms,
α
n=1
=
9a
3
0
2Z
4
. (13.57)
Table 13.4 lists the relativistic values for the ground
state polarizability α
n=1
rel
, obtained by calculating (13.55)
Part B 13.4
Atoms in Strong Fields 13.5 Recent Developments 233
using relativistic variational basis sets [13.10]. The val-
ues are interpolated by
α
n=1
=
a
3
0
Z
4
9
2
−
14
3
(αZ)
2
+0.53983(αZ)
4
.
(13.58)
13.4.4 Other Stark Corrections
Third Order Corrections
For the energy correction cubic in the external field
(13.36), one obtains [13.9]
E
(3)
=
3
32
F
3
n
Z
7
× δ
n
23n
2
−δ
2
n
+11m
2
l
+39
. (13.59)
Relativistic Linear Stark-Shift
of the Fine Structure of Hydrogen
For a Stark effect small relative to the fine structure, the
degenerate levels corresponding to the same value of j
split according to
δ
m
E
nj
=
3
4
n
2
−
j +
1
2
2
nm
j( j +1)
F .
(13.60)
Other Stark Corrections in Hydrogen
The expectation value of the delta function, is, in a.u.
[13.11],
2π1s|δ(r)|1s=2 −31F
2
. (13.61)
Table 13.4 Relativistic dipole polarizabilities for the
ground state of hydrogenic atoms
Z α
n=1
rel
Z
4
/
a
3
0
1 4.499 7515
5 4.493 7883
10 4.475 1644
20 4.400 8376
30 4.277 5621
40 4.106 2474
50 3.888 1792
60 3.625 0295
70 3.318 8659
80 2.972 1524
90 2.587 7205
100 2.168 6483
For the Bethe logarithm β defined by
β
1s
=
n
|
1s
|
p
|
n
|
2
(E
n
− E
1s
) ln
|
E
n
− E
1s
|
n
|
1s
|
p
|
n
|
2
(E
n
− E
1s
)
,
(13.62)
the result is [13.12]
β
1s
= 2.290 981 375 205 552 301
+0.316 205(6) F
2
. (13.63)
These results are useful in calculating an asymptotic
expansion for the two-electron Bethe logarithm [13.13].
13.5 Recent Developments
The drastic change of an atom’s internal structure in
the presence of external electric and magnetic fields
is shown most clearly through the changes induced in
its spectral features. Of these features, avoided cross-
ings are a distinctive example. Recent work in this
area by Férez and Dehesa [13.14] has suggested the
use of Shannon’s information entropy [13.15], defined
by
S =−
ρ(r) ln ρ(r)dr ,
(13.64)
where ρ(r) =|ψ(r)|
2
, as an indicator or predictor of
such irregular features of atomic spectra. By studying
some excited states of hydrogen in parallel fields it was
shown that, for the states involved, a marked confine-
ment of the electron cloud and an information-theoretic
exchange occurs when the magnetic field strength is ad-
justed adiabatically through the region of an avoided
crossing. The field strengths studied are characteristic
of compact astronomical objects, such as white dwarfs
and neutron stars.
Although the effects of strong magnetic fields on
the structure and dynamics of hydrogen have been
known for some time, knowledge of the helium atom
in such fields has only recently become sufficient for
comparison with astrophysical observations [13.16–18].
As one example of their importance, such studies
have proven critical in showing the presence of he-
lium in the atmospheres of certain magnetic white
dwarfs [13.19].
In recent years, the increased sophistication and
resolution of observation techniques has not only in-
Part B 13.5
