Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

68 Energy in planetary processes

1.7 Compare the expansion work associated with vaporization of 1 kg of water at 1 bar

to that of conversion of 1 kg of kyanite to sillimanite at 3 kbar. The molar volumes

in J bar

−1

mol

−1

are: liquid water = 1.807, sillimanite = 4.986, kyanite = 4.415.

Assume that water vapor at 373 K and 1 bar is an ideal gas.

1.8 Starting from equation (1.18), derive the complete equation for expansion work of

a sphere, and show why (1.19) is an acceptable approximation for an infinitesimal

expansion.

1.9 Derive the exact expression for the energy stored during a change in volume from V

to V , caused by a change in pressure from P

to P, of an elastic solid with constant bulk

modulus K

. (Hint: this is a good opportunity to practice your Maple.) Compare this

expression with equation (1.31), and discuss the conditions under which the constant

volume assumption is no longer tenable.

1.10 Derive an equation that relates elastic energy stored per unit volume (equation (1.37))

to change in gravitational potential per unit volume (mass stays constant, what changes

is elevation). The bulk modulus of silicate minerals is of order 1000 kbar, their density

∼3000 kg m

−3

, and g = 9.8ms

−2

. Assume that an earthquake causes uplift of 1 m.

Estimate the strain that was released (the non-dimensional quantity ε). How does this

value vary with bulk modulus? Comment on your results.

1.11 Derive K

, β

and α for an ideal gas, starting from the ideal gas EOS.

1.12 Bulk modulus and coefficient of thermal expansion are two ways of relating the three

variables, P ,V ,T . There is a third one, that is to take the derivative of P relative to

T at constant V. This gives rise to another material property known as the Grüneisen

parameter and symbolized by γ . The Grüneisen parameter measures the increase in

pressure caused by heating at constant volume. It can be defined as follows:

γ =



∂P

∂T



Show that the Grüneisen parameter of an ideal gas is a constant, and that it is related

to α and K

by:

γ =

αK

1.13 Derive a general equation that relates Cp to Cv in terms of material properties. Use it

to show that for an ideal gas Cp = Cv + R. Discuss why for solids and liquids it is Cp

≈ Cv.

1.14 Estimate a possible range of heating rates (dT/dt) by viscous dissipation along sub-

duction zone megashears. Can this be a significant contribution to the origin of arc

magmatism?

For the following problems use standard state thermodynamic data from Holland and

Powell (1998).

1.15 Calculate the enthalpy of formation of diamond at 1 bar, 298.15 K and at 1 bar, 1000 K.

Do this by hand and using the Maple procedures described in Software Box 1.1.

1.16 Use the Maple procedures described in Software Box 1.1 to calculate the enthalpy

change of the spinel–garnet transition (reaction (1.94)) at 1 bar, 298.15 K and at 1 bar,

1000 K. You should get ∼ 23.29 kJ and 11.76 kJ, respectively. If you don’t, you need

to practise your Maple.

69 Exercises for Chapter 1

1.17 Calculate the enthalpy change of the oxidation of fayalite to hematite + quartz at 1

bar, 298.15 K. Is this reaction endothermic or exothermic?

1.18 Average terrestrial heat flux is 80 mW m

−2

. At what rate musta1mthick slab of

fayalite oxidize in order to supply energy at this rate? (Hint: you need the density

fayalite but Holland and Powell supply its molar volume.) Supposing that the energy

yield of fayalite oxidation is typical of silicate chemical reactions, what can you

conclude about the source of the Earth’s internal heat? You will need to develop some

scaling arguments, and to ignore for now heat transfer complications.

Energy sources in planetary bodies

Planetary bodies can be thought of as combinations of heat reservoirs and heat engines.

The heat reservoirs store internal energy, E, and the heat engines convert some of this

thermal energy into various types of mechanical, electrical and chemical energies. This

simple physical picture is true of all active planetary bodies, regardless of their composition

(rocks, gases or ices) or size. The details, however, vary widely throughout the Solar System.

In this chapter we discuss the storage of thermal energy in planetary bodies.

We begin by distinguishing internal from external heat reservoirs, and we define the

latter as those that derive their energy from solar electromagnetic radiation. External heat

reservoirs occur in surface and near-surface environments. Examples include the Earth’s

oceans and atmosphere. Internal heat reservoirs store energy at various depths, from near-

surface environments to the planet’s core. They are fed by dissipation of various types

of non-thermal energy but there is one unifying characteristic, which is that dissipation

takes place deep enough that the rate of heating exceeds the rate of heat transfer to the

planet’s surface (Chapter 3). The relative magnitudes of the energy fluxes from external and

internal reservoirs at a planet’s surface vary widely among the bodies of the Solar System.

In solid planetary bodies (rocky and icy) surface energy flux is typically dominated by solar

radiation, despite the fact that internal energy reservoirs in some of them are large enough

to make noticeable, perhaps dominant, contributions to the planet’s surface features. At the

present time the surfaces of Earth, Venus, Io, Europa, Ganymede, Titan, Enceladus and

Triton are being affected by processes fueled by internal energy reservoirs. In contrast,

internal energy reservoirs for Mars, Mercury, the Moon, most other satellites of the giant

planets and the asteroids appear to be negligible, but this was certainly not true at earlier

times, as shown for instance by the huge Martian volcanoes and the Lunar maria. Internal

energy reservoirs dominate surface energy fluxes in the fluid planets Jupiter, Saturn and

Neptune. The relentlessly violent weather patterns of Jupiter and Saturn are driven by energy

extracted from those planets’internal heat reservoirs, in stark contrast with Earth’s weather,

which is driven by solar energy. The contributions of internal and external reservoirs may

be more or less evenly matched in Uranus.

Here we focus on the sources of planetary internal energy and on the pathways by which

non-thermal energy is dissipated. Ultimately, the possible sources of thermal energy are just

three: dissipation of gravitational potential energy, dissipation of nuclear binding energy,

and dissipation of electrical energy. Gravitation was the chief internal energy source in

the formative stages of all planets, and is still today the dominant internal energy source in

some of the moons of the giant planets, and perhaps in Saturn as well. Radioactive heating is

dissipation of nuclear binding energy. At present it is an important source of energy in some

rocky planets (notably Earth, almost certainly Venus as well), and was even more important

in the early Solar System, as a result of the greater abundances of long-lived radioactive

isotopes (

232

Th,

235

U and

238

U) and of the existence of short-lived radioisotopes that

are now extinct (chiefly,

Al,

Fe and

Mn). Dissipation of electrical energy by ohmic

71 2.1 Planetary heat ﬂows

heating occurs if a planet with an electrically conductive layer is immersed in a time-varying

magnetic field (Section 1.8.3). It may have been important in the early Solar System if the

magnetic field of the nascent Sun was orders of magnitude stronger than today’s.

2.1 Planetary heat ﬂows

Planets are bathed by solar electromagnetic radiation with a spectrum that corresponds to

black body emission at the temperature of the solar photosphere, ∼6000 K (Section 12.2).

This spectrum peaks in the range of visible wavelengths (∼0.4–0.8 µm) or, more accurately,

this is the range of visible wavelengths because we evolved on a planet in which most of

the energy that reaches us from the central star is in this range of wavelengths. Some of this

energy is immediately reflected back to space. The balance is thermalized, which means that

it is absorbed by the planet’s atmosphere and solid or liquid surface (if the planet has one)

and eventually radiated back to space in the infrared part of the spectrum, with wavelengths

of the order of 5–200 µm.

Electromagnetic radiation is described by the Stefan–Boltzmann law, which we will

discuss in more detail in Chapter 13. The total amount of energy radiated per unit area and

per unit time (called the radiated energy flux, where flux means quantity per unit of area

per unit of time), also called the irradiance, is symbolized by F and given by:

F = σT

. (2.1)

In this equation σ is a constant known as the Stefan–Boltzmann constant (Appendix 1), T is

the absolute temperature and  is a parameter ( ≤1), called emissivity, which describes the

efficiency with which the body radiates electromagnetic energy. For a perfect black body,

i.e. a body that emits radiation with equal efficiency at all wavelengths,  = 1. If a planet

is in thermal equilibrium with solar radiation and the planet has no internal heat flow then

its energy output, F

, would derive only from thermalized sunlight and would correspond

to emission from a black body at a temperature T

, given by equation (2.1) and called the

planet’s equilibrium temperature (we will discuss this in detail in Section 13.2).The values

of F

and T

are calculated on the basis of the incident solar flux and the planet’s albedo,

A, which is the fraction of incident sunlight that is reflected back to space (see, for example,

Hubbard, 1984; de Pater & Lissauer, 2001).

The measured infrared emission of a planet, F

, is not necessarily equal to the calculated

value of the equilibrium thermalized flux, F

. The measured value of F

yields the planet’s

effective temperature, T

(equation (2.1)). If T

then the planet liberates internal

heat. The internal heat flux, q, is given by (this equation is derived rigorously in Section

13.3.2, equation (13.35)):

q = F

−F

=σ



−T



. (2.2)

In practice, given the uncertainties in the measurements of F

, in the albedo, A (which

enters in the calculation of T

), and in the emissivity /, a planet’s internal heat flux can

be determined in this way only if q, F

and F

are of the same order of magnitude. This

is true for Jupiter, Saturn, Neptune and Io, and is how the average internal heat fluxes for

these bodies (given in Table 2.1) have been determined. For Uranus T

appears to be only

slightly greater than T

, so that Uranus’s internal heat flux remains somewhat uncertain.

72 Energy sources in planetary bodies

Table 2.1 Planetary heat ﬂow parameters

Planet q(W m

−2

) q

(W kg

−1

) T

(K) T

(K)

Earth 0.08 6.40 ×10

−12

263

Moon 0.03 1.34 ×10

−11

277

Mars 0.04 9.00 ×10

−12

222

Io 2.50 1.17 ×10

−9

100 109

Jupiter 5.44 1.76 ×10

−10

113 124

Saturn 2.01 1.51 ×10

−10

83 95

Uranus 0.04 3.91 ×10

−12

58 59

Neptune 0.43 3.22 ×10

−11

48 59

Values of q from Lodders and Fegley (1998), except Mars, from Carr (1999).

Values of q

calculated from q and planetary data from Lodders and Fegley (1998).

Values of T

and T

from de Pater and Lissauer (2001), except Io from Hubbard (1984).

For all the terrestrial planets q F

, so that q must be measured directly (in Chapter 3 we

will discuss how). Such direct measurements have only been carried in the Earth and Moon,

but whereas the terrestrial value listed in Table 2.1 is an average of hundreds of thousands

(if not millions) of measurements, the lunar value is an average of only two, at the Apollo 15

and 17 landing sites, and thus of very uncertain significance. The Martian heat flux listed

in Table 2.1 (after Carr, 1999) is an estimate based on geochemistry (areochemistry?),

which we discuss further below and in Chapter 3. No numerical estimates are available

for the other terrestrial planets nor for the major moons of the giant planets (except Io),

but some qualitative statements are possible. Given Venus’s many active volcanoes and

similarity to Earth in size and density (probably reflecting a similarity in composition) it is

not unreasonable to suppose that its time-averaged heat flux may be comparable to that of

Earth – the reason for the qualifier “time-averaged” will become clear in Chapter 3. The

Jovian moons Europa and Ganymede, Saturn’s moons Titan and Enceladus and Neptune’s

moon Triton all display youthful surfaces, and in some cases visibly active processes of

internal origin as well, implying the existence of non-negligible internal heat flows.

The contributions of internal and external heat reservoirs in shaping a planet’s surface can

be gauged by comparing the equilibrium thermalized solar flux F

, to its internal heat flux,

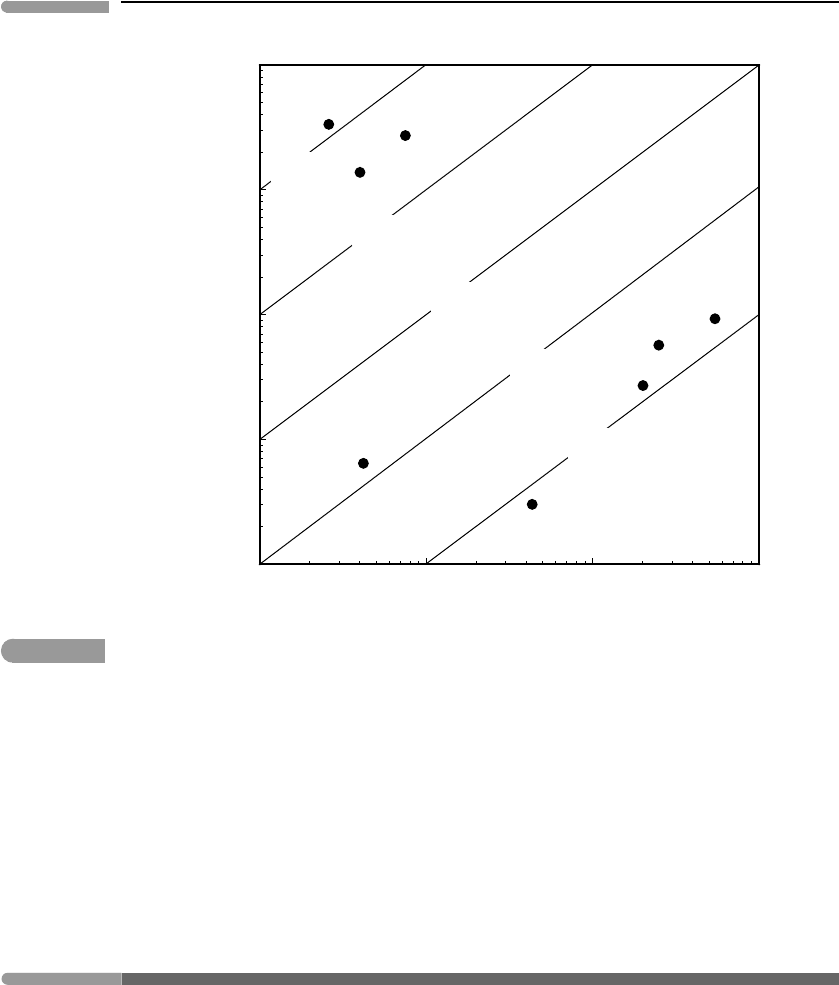
q (Fig 2.1). With the notable exception of Io, the thermalized solar flux on the surfaces of

the solid planets is 10

–10

times greater than the internal heat flux. A way of interpreting

this difference is that, on average, the rate of external processes is a few orders of magni-

tude faster than that of internal processes. An equivalent statement for Earth is that active

mountain building and active volcanic areas affect a small fraction of the planet’s surface,

whereas climate, the hydrologic cycle and the biosphere cover the entire planet. In contrast,

the entire surface of Io is volcanically active (see, for example, Davies, 2001). Solar energy

fluxes in the giant planets are 2–3 orders of magnitude less than in the terrestrial planets.

The Dutch–American planetary astronomer Gerard Kuiper noted in the 1950’s that this

presented a problem in view of the weather systems observed in Jupiter and Saturn, which

are much more violent and constant than those of Earth. He inferred that these planets must

have a large internal energy output (Kuiper, 1952), and this is indeed the case. In the giant

planets (except perhaps Uranus) and Io internal heat flux is 10–100 times greater than in

73 2.2 Dissipation of gravitational potential energy

0.01 0.1 1

0.1

100

1000

Internal heat flux ( W m

–2

)

Thermalized solar radiation ( W m

–2

)

Earth

Moon

Mars

Jupiter

Saturn

Uranus

Neptune

Fig. 2.1

Thermalized solar radiation compared to internal heat ﬂux of some Solar System objects. Internal heat ﬂuxes of Mars

and Moon are highly uncertain.

the terrestrial planets, and of the same order of magnitude as the thermalized solar flux

(Fig. 2.1).

A useful parameter when comparing planets and energy dissipation mechanisms is the

planetary heat flow per unit mass, q

, which is also listed in Table 2.1. Io is the largest

anomaly, with a heat flow per unit mass some three orders of magnitude greater than that

of Earth, and 1–2 orders of magnitude greater than those of the giant planets.

2.2 Dissipation of gravitational potential energy

Assembly of planets by coalescence of dust particles and gas molecules is accompanied

by liberation of gravitational potential energy (Section 1.3.1). Planetary growth almost

certainly takes place in different stages. The details of the various processes involved are

not fully understood and may have differed for rocky vs. fluid planets (see, for example,

Chambers, 2005). Regardless of the exact pathway, however, the gravitational potential

energy of the diffuse mass of nebular material that ends up being a planet is ultimately

dissipated as heat. Part of this heat is stored in the planet as internal energy, E. Dissipation

of gravitational potential energy is the most important source of internal energy during

74 Energy sources in planetary bodies

Accretion Contraction Differentiation

Fig. 2.2

Three pathways for dissipation of gravitational potential energy.

planetary formation, and is also responsible for heating of proto-stars up to the point at

which thermonuclear fusion begins and they become true stars.

For the sake of mathematical clarity, we distinguish among three mechanisms that convert

gravitational potential energy to thermal energy: accretion, contraction and differentiation

(Fig. 2.2). I define accretion as a process during which planetary mass increases while

density and mass distribution remain constant. Contraction and differentiation entail mass

redistribution at constant total mass. The following is more specific.

Accretion corresponds to assemblage of the planet from particles that are initially con-

sidered to be gravitationally unbound to one another. Planetary mass grows with time and

the gravitational potential energy of the added matter is dissipated as heat. We will make

the simplifying assumption that the result of accretion is a planetary body of homogeneous

composition and density. Assembly of the terrestrial planets is probably best modeled as

accretion.

Contraction dissipates gravitational potential energy at constant mass as a result of

a decrease in planetary radius, and consequent increase in density (equation (1.6)). This

mechanism may be an appropriate model for the formation and early evolution of fluid

planets, and is also the mechanism responsible for heating proto-stars.

Differentiation of an initially homogeneous planet entails separation of a dense phase

that sinks towards the center of the planet relative to a less dense phase that comes to

occupy its outer layer. The mass redistribution that accompanies differentiation dissipates

gravitational potential energy. The resulting thermal energy is in this case deposited in the

deep planetary interior, so that this mechanism may be particularly efficient in augmenting

a planet’s internal energy content. It is thought to be of critical importance in the thermal

evolution of both solid and fluid planets.

Tidal dissipation is another source of internal energy that, ultimately, relies on gravita-

tional potential energy. The pathway by which mechanical energy is dissipated by tides is,

however, different from the other processes and will be discussed separately.

Accretion, contraction and differentiation may operate simultaneously or successively

during planetary evolution. The terrestrial planets almost certainly formed by accretion, but

it is less clear whether the fluid planets are chiefly the result of accretion or of contraction

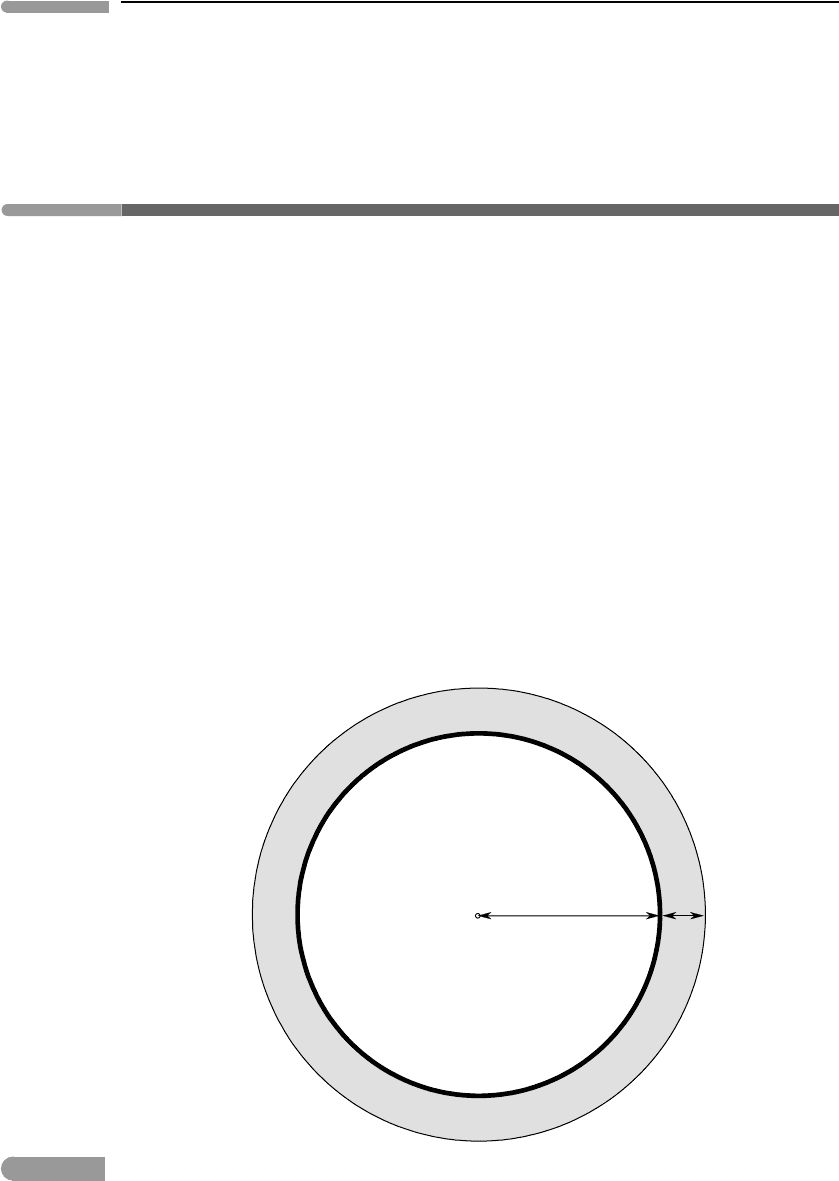
75 2.3 Gravitational binding energy

of a mass of diffuse nebular material, or a combination of both processes. The purpose of

the following sections is to develop the mathematical description of the various aspects of

gravitational heating, rather than to elucidate the mode of formation of any particular planet.

2.3 Gravitational binding energy

The total amount of gravitational potential energy liberated during formation and subsequent

evolution of a planetary body to a given point in time is measured by its gravitational

binding energy, U

, at that time. The magnitude of a planet’s gravitational binding energy

provides clues and constraints about the planet’s thermal history and internal energy sources.

The concept of gravitational binding energy is analogous to that of lattice energy of a

crystal (Section 1.8.2), except that during formation of a crystal the potential energy that

is dissipated arises from work performed by electrostatic rather than gravitational forces.

Calculation of gravitational binding energy is generally much simpler than calculation of

lattice energies.

Consider the assembly of a self-gravitating celestial body by infinitesimal mass incre-

ments. Self-gravitating means that the body is held together only by gravitational forces

arising from the mass of the body itself. Planets and stars are obvious examples of self-

gravitating celestial bodies, and so are larger structures such as galaxies and galaxy clusters.

Consider a body with spherical symmetry and let m be the mass of the sphere of radius r

(Fig. 2.3). Addition of an infinitesimally thin shell, dr, results in a mass increment dm

and changes the gravitational binding energy of the planet by an amount dU

equal to the

gravitational potential energy of the added mass. From equation (1.6) we have:

Fig. 2.3

Calculation of gravitational binding energy. Each inﬁnitesimal shell of thickness dr adds an amount of mass dm to the

planet.

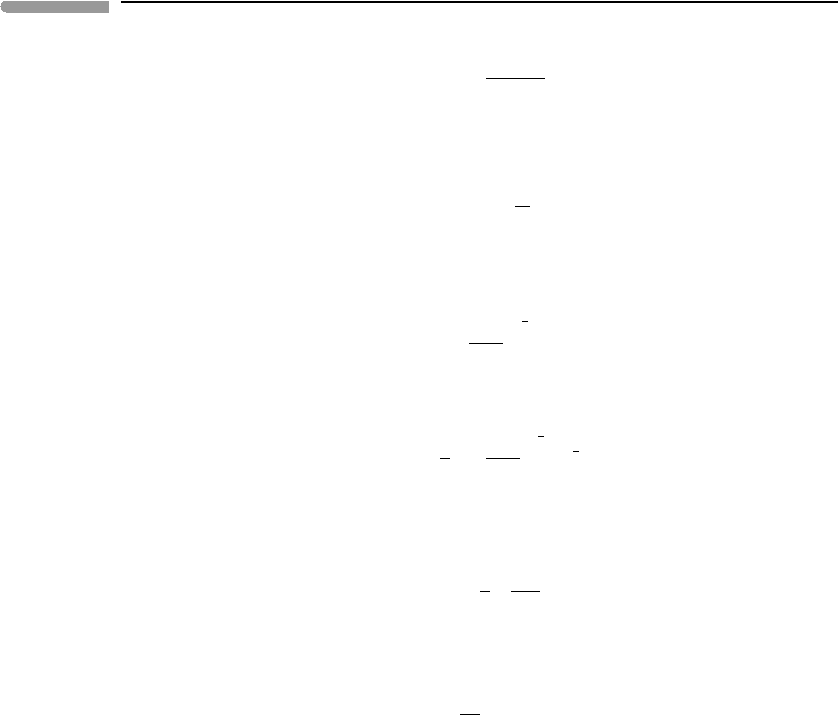
76 Energy sources in planetary bodies

=−

Gmdm

. (2.3)

The gravitational binding energy of the fully assembled planet is obtained by integrating

this expression over the mass of the planet, M:

=−G



dm. (2.4)

We assume initially that the planet is homogeneous and with mean density ρ. Radius is then

simply related to mass by:

r =



4πρ



. (2.5)

Substituting into equation (2.4) and integrating:

=−



4πρ



. (2.6)

Calling R the radius of the planet of mass M, we use equation (2.5) in order to simplify

equation (2.6) to:

=−

, (2.7)

which yields the gravitational binding energy U

of a homogeneous planet of mass M and

radius R. In terms of R and ρ:

=−

Gπ

. (2.8)

This is the total amount of gravitational potential energy that has been converted to other

types of energy in order to make a homogeneous planet with density ρ =M(4/3π)

−1

−3

Gravitational binding energy may be transiently converted to kinetic energy of dust grains

or planetesimals, but it is ultimately dissipated as heat, when these particles stick together

following inelastic collisions (Section 1.3.2). Gravitational binding energy is always a

negative quantity (see equations (2.7) and (2.8)). An increase in its absolute magnitude

(U

< 0) corresponds to energy dissipation and can be the result of an increase in mass

(accretion), a decrease in radius at constant mass (contraction) or redistribution of denser

material towards the center of the planet, also at constant mass (differentiation).

During formation and evolution of a planet gravitational binding energy may be either

stored as internal energy or radiated to space. The relative magnitude of these two terms

depends on the rate and mode of dissipation of mechanical energy and on the material

properties of the planet. We will examine thermal evolution during accretion and contraction

in Sections 2.4 and 2.5, respectively. Planetary differentiation leads to an additional release

of gravitational binding energy that is not included explicitly in equation (2.7), and that we

calculate in Section 2.6. Before refining our analysis, however, we will carry out a rough

estimate of the gravitational binding energies of planetary bodies on the basis of only their

sizes and mean densities, and draw some conclusions about their thermal histories and

possible energy sources.

77 2.3 Gravitational binding energy

Worked Example 2.1 Gravitational binding energy and heat flow

Let us compare observed planetary heat flows (Section 2.1) with the heat flows that could

be expected if all the gravitational binding energy of a planet had been stored as internal

energy during formation of the planet and then released at a constant rate over the age of

the Solar System. If the average heat flux (energy per unit of area per unit of time) of a

planet of mass M and radius R is q, the heat flow per unit mass q

(listed in Table 2.1)is

given by:

4πR

. (2.9)

The binding energy per unit mass is (from equation (2.7)):

=−

. (2.10)

If this gravitational binding energy was dissipated at the beginning of the Solar System and

stored as internal energy, and the internal energy was then released at a constant rate since

then, we should observe an internal heat flow per unit mass of order q

≈ u

, where

= 4.55 ×10

years = 1.44 × 10

s is the age of the Solar System. Values of q

and

for various planetary bodies are plotted in Fig. 2.4. Ignoring for a moment Mars and

the Moon (because heat fluxes for these two bodies are poorly constrained, see Section 2.1),

–12

–11

–10

–9

–

–12

–11

–10

–9

–8

over age of the Solar System

Heat flow per unit mass (q

WKg

–1

)

Binding energy per unit mass (q

WKg

–1

)