Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

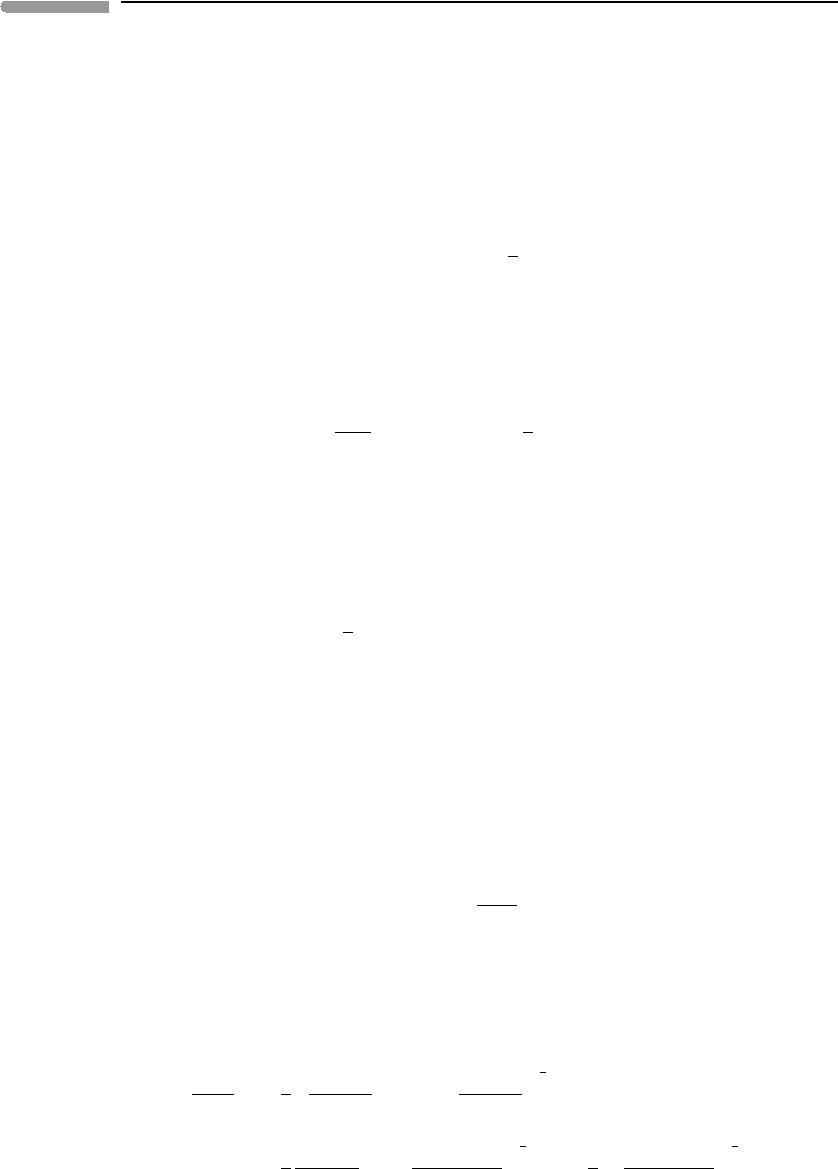
98 Energy sources in planetary bodies

Gravitational potential energy inside a self-gravitating body is described by an equation

that is different from equation (1.6), because the gravitational force at a point inside the

body arises only from the mass internal to that point (this result, which was first derived by

Newton, is demonstrated in Box 2.1). The equations are simpler if we work with gravitational

potentials. If we call the gravitational potentials of a characteristic volume element (one that

falls from r

to r

) before and after differentiation Φ

g,i

and Φ

g,f

, respectively, we have:

U



g,f

−Φ

g,i



πr

(

−ρ

)

. (2.57)

In the initial state the characteristic volume element is located at a radius r

inside a solid

sphere of radius R and homogeneous density ρ

. The gravitational potential at that point is

given by (Box 2.1):

g,i

=−



−r



=−

πGρ



−r



. (2.58)

In the final state the characteristic element is located at radius r

inside a homogeneous

sphere of radius r and density ρ

, which is in turn enclosed by a shell of homogeneous

density ρ

extending between radii r and R (Fig. 2.13). The value of Φ

g,f

is obtained by

adding these two contributions and is given by:

g,f

=−

πGρ



−r



−2πGρ



−r



, (2.59)

where the first term is the gravitational potential due to the inner sphere (the core), and the

second term is the gravitational potential arising from the spherical shell surrounding the

core (i.e. the mantle) – see Box 2.1.

The release of gravitational potential energy caused by differentiation increases the (abso-

lute magnitude) of the planet’s gravitational binding energy. A useful measure of the amount

of energy dissipated during core formation is the non-dimensional ratio that compares this

energy to the gravitational binding energy of the undifferentiated planet:

D =

U

, (2.60)

where U

is the binding energy of the undifferentiated planet, equation (2.8). Substituting

equations (2.58) and (2.59)in(2.60) and using (2.54) to eliminate the radii we arrive, after

some algebraic manipulations, at:

D =

U

=−



−ρ





1 −



−ρ





−

−ρ





−ρ

(

−ρ

)



−ρ



−ρ

(

−ρ

)





(2.61)

99 2.6 Differentiation

We can write this equation in terms of the ratios between the densities of the core and mantle

and the planet’s bulk density, ρ

. Defining the ratios ϕ

=ρ

/ρ

and ϕ

=ρ

/ρ

, we get:

D =

U

=−

(

1 −ϕ

)



1 −



−ϕ

1 −ϕ





−

(

1 −ϕ

)





1 −ϕ

(

−ϕ

)



−



1 −ϕ

(

−ϕ

)





(2.62)

and also:



1 −ϕ

−ϕ



. (2.63)

These two non-dimensional equations are plotted in Fig. 2.15. The curves are contours of

constant D, as defined by equation (2.62), and the straight lines are contours of constant

core radius relative to planetary radius, given by equation (2.63). The graph leads to two

conclusions that should be intuitively obvious. First, the thermal contribution that arises

from formation of a small core is relatively minor and not very sensitive to the density of

the core. The small size of the core limits the value of m

(equation (2.55)) and hence the

available amount of gravitational potential energy. Note, however, that even for a planet like

Mars, which is likely to have a relatively small core, differentiation may dissipate a fraction

of order 10

−2

of the planet’s binding energy, which may be comparable to the internal

energy stored by accretion (Worked Example 2.4). Second, in planets with a large core,

the thermal effect of core formation is strongly dependent on the density contrast between

mantle and core, because this is what ultimately determined the magnitude of m

Worked Example 2.4 Thermal effect of core formation in the terrestrial planets

Typical values of specific heat capacity and enthalpy of fusion for rocky materials are

Jkg

−1

and 5 × 10

Jkg

−1

, respectively. The values for iron are approximately

one half of these (see also Section 1.14.3). Density values for Earth are ρ

=5500 kg m

−3

≈4500 kg m

−3

, and ρ

≈10700 kg m

−3

(you should confirm that these values yield the

correct radius for the Earth’s core, ∼3480 km). Plugging these densities into equation (2.62)

we get D = 0.118 (see also Fig. 2.15). From equation (2.10) we get the binding energy per

unit mass of the Earth, u

≈ 3.75 ×10

Jkg

−1

. We can then conclude that formation of

the Earth’s core dissipated ∼4.43 × 10

Jkg

−1

. This is enough thermal energy to raise

the temperature of the entire Earth by over 4500 K, or to melt the entire Earth more than

10 times over! Upon formation, the core must have been completely molten, and perhaps

superheated above its liquidus temperature too. Part of the gravitational energy dissipated

was stored as enthalpy of melting. Metal solidification over the age of the Solar System,

that continues to this day, releases this enthalpy from the liquid metal thermal reservoir.

This is one of the sources of energy that powers convection in the Earth’s core and mantle

(Chapter 3).

100 Energy sources in planetary bodies

0.5 0.6 0.7 0.8 0.9 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.1

0.2

0.3

0.4

0.5

0.6

0.8

Earth

Jupiter

Mercury

Neptune

Mercury

Mars

Saturn

0.5 0.6 0.7 0.8 0.9 1

1.5

2.5

0.1

0.2

0.3

0.4

0.2

0.3

0.4

0.5

0.6

0.7

Earth

Mercury

Mars

/ρ

Fig. 2.15

Curves of constant D (equation (2.62)) and constant r/R (equation (2.63), straight lines) as a function of the density

ratios ϕ

and ϕ

. The lower panel magniﬁes the region of ϕ

values characteristic of terrestrial planets. Two different

locations are shown for Mercury and Mars, representing different assumed core and mantle density values (see text).

Core and mantle densities are far less well constrained for the other terrestrial planets.

Mercury appears to have the largest core among the terrestrial planets, with r/R ≈0.6–0.7

(this can be inferred from the planet’s high uncompressed density, see, for example, Strom,

1999). A core of this size allows relatively large D values (Fig. 2.15), which might be an

important point in understanding the planet’s thermal history given that Mercury appears

101 2.6 Differentiation

to still have a partially molten core and a faint magnetic field (Strom, 1999; Purucker et al.,

2009). For example, if we assume ρ

=3700 kg m

−3

and ρ

=9500 kg m

−3

, and given that

for Mercury ρ

=5430 kg m

−3

,wegetr/R =0.67 and D ≈0.20. If these values are correct

then formation of the Mercurian core may have liberated ∼1.1 ×10

Jkg

−1

, three times

what would be needed to melt the entire planet. Because of Mercury’s large core this result

is sensitive to core and mantle densities. However, even assuming ρ

= 4000 kg m

−3

and

= 8300 kg m

−3

, which are probably extreme permissible values given what we know

about Mercury’s composition (e.g. a low-Fe crust, Strom, 1999; Taylor & Scott, 2005), we

get D ≈0.15 (Fig. 2.15) and an energy dissipation of ∼8.4×10

Jkg

−1

, which is still twice

the amount of energy needed to melt the entire planet. Data from the Messenger mission

may allow a refinement of these calculations.

In contrast to Mercury, what we know about the composition of Mars, coupled to its

low bulk density, suggests that Mars has a relatively small core, with r/R ≈ 0.3 −0.4 (see

Wanke & Dreibus, 1988; Lodders & Fegley, 1997; Sanloup et al., 1999). Core and mantle

densities may be in the range ρ

= 3600 −3800 kg m

−3

and ρ

= 8000 −10000 kg m

−3

respectively (McSween, 2005), which yield D ≈ 0.02 −0.06. The largest of these values

yields an energy dissipation during core formation of ∼4.5 ×10

Jkg

−1

, which may have

been just enough to melt the planet. The energy dissipated at the lower end of the range

may have been sufficient to melt the Martian core but not the entire planet.

Application of the results summarized in Fig. 2.15 to the giant planets is less straight-

forward because, in at least some of them, differentiation may have taken place on more

than one level. All giant planets are thought to have very dense cores composed of rocky

material and C–H–O–N compounds – “ices” in the terminology of planetary sciences (Guil-

lot, 1999, 2005). These cores, however, are almost certainly quite small (r/R ≈ 0.1–0.2),

so that, even if they formed by differentiation from initially homogeneous bodies, their

formation is unlikely to have made a large contribution to the internal energy contents of

the giant planets (Fig. 2.15). If the giant planets formed by collapse of gaseous material

around earlier accreted dense rocky cores (Thommes et al., 2003) then the rocky cores may

have undergone differentiation but the contribution of this process to the heat budget of

the full giant planets may still have been relatively minor, compared to the early stage of

Kelvin–Helmholtz contraction.

Amore important contribution of differentiation to the thermal budget of some of the giant

planets may arise from immiscibility between liquid metallic hydrogen and atomic helium

(Stevenson & Salpeter, 1977; Hubbard, 1980; Stevenson, 1982a; Hubbard et al., 1999;

Guillot, 1999; Fortney & Hubbard, 2004). Hydrogen and helium are the chief constituents

of Jupiter and Saturn and are also abundant in Uranus and Neptune, although the bulk

compositions of the two ice giants are not as well constrained as those of the two gas giants.

In their molecular or atomic forms, hydrogen and helium are miscible in all proportions.

Hydrogen, however, undergoes pressure ionization (Section 1.15) at lower pressure than

helium. A miscibility gap exists between liquid metallic hydrogen and atomic helium, that

closes with increasing temperature (Stevenson & Salpeter, 1977; Chabrier et al., 1992;

Saumon et al., 1992, 1995; Morales et al., 2009; Lorenzen et al., 2009). The P –T slope

of the boundary that terminates the miscibility gap is poorly known, but it is possible that

a planet’s thermal gradient may cross it with increasing depth, as shown schematically in

Fig. 2.16. The two phases separate at the plasma phase transition (where hydrogen undergoes

pressure ionization) and the denser helium “rains out” towards the planet’s center, down to

102 Energy sources in planetary bodies

a depth at which the temperature is high enough that the solvus disappears, at which depth

the helium raindrops redissolve in the liquid metallic hydrogen. Dissipation of gravitational

potential energy takes place by friction between the sinking helium drops and the metallic

hydrogen medium. This process is thought to be ongoing at the present day in Saturn, and to

be an important contributor to its observed heat flux (recall that Saturn’s heat flux per unit

mass is the highest relative to its binding energy per mass among all fluid planets, Fig. 2.4).

Because of Jupiter’s higher internal temperatures, the region of H–He immiscibility in it

may be much smaller than in Saturn, or altogether absent, so that He differentiation in

Jupiter may not be taking place at present.

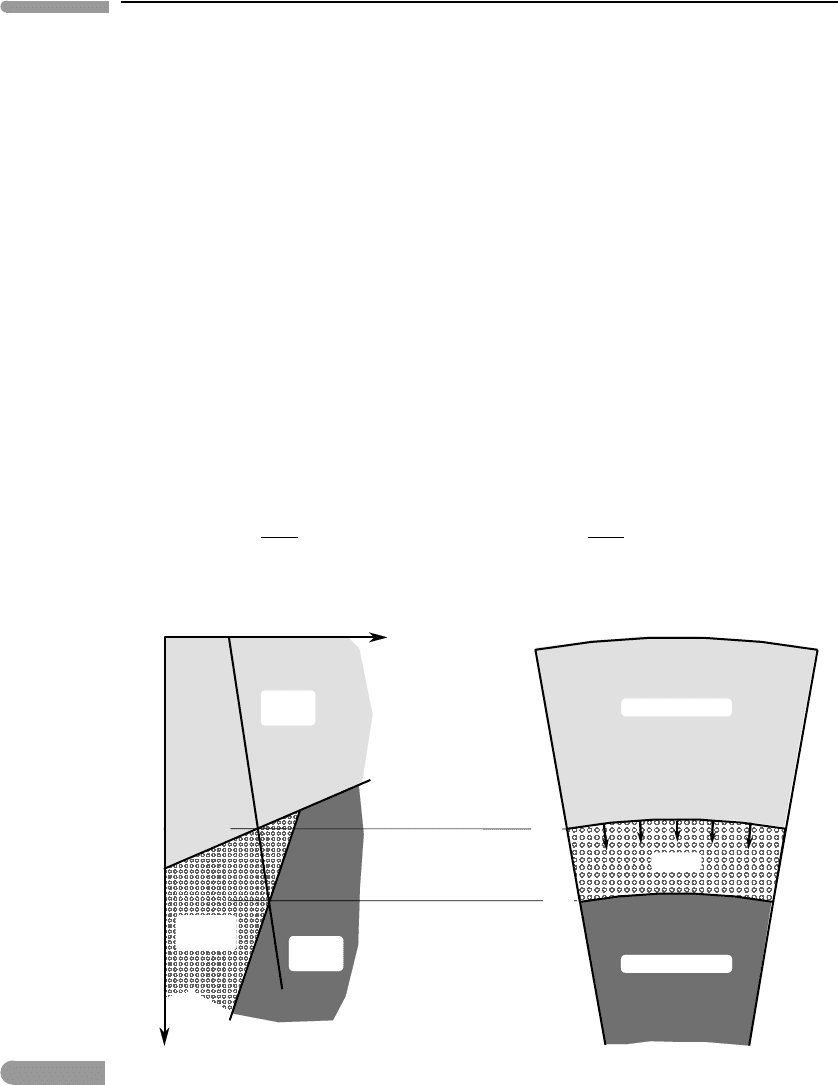
We now seek an estimate of the helium sinking rate that would be needed to sustain

a given planetary heat flow. Let the top and bottom of the two-phase region lie at radii

= z

R and r

= z

R, where R is the planet’s radius (Fig. 2.16). As the planet ages and

cools we expect this region to move towards the planet’s center, effectively scavenging He

from its outer layers and concentrating it in the planet’s interior. As this happens, helium

raindrops form at the top of the two-phase layer and redissolve at the bottom, so that each

volume element of helium falls from r

to r

, in the process exchanging places with an

equal volume of hydrogen. The difference in gravitational potential between the top and

bottom of the two-phase layer is given by (Box 2.1 and equation (2.58)):

Φ

=−



−r



−



−r



=−



−z



. (2.64)

1phase

– He

1phase

– He

2 phases

+He

planet’s thermal gradient

He-depleted layer

He-enriched layer

He rain

plasma phase transition

Fig. 2.16

Schematic diagram showing the behavior of H–He mixtures with temperature and pressure. Liquid molecular

hydrogen (H

) ionizes at the plasma phase transition and becomes liquid metallic hydrogen (H

), which is immiscible

with He at low temperature but becomes miscible at high temperature. Depending on the planet’s thermal gradient,

immiscibility may occur over a limited depth interval, leading to the behavior depicted in the ﬁgure, that is thought to

be a plausible model for Saturn’s interior. Jupiter’s interior may be hot enough to miss the miscibility gap. Pressures in

Uranus and Neptune are everywhere lower than the plasma phase transition. See also Fig. 1.16.

103 2.7 Tidal dissipation of mechanical energy

The helium droplets probably attain their terminal velocity soon after forming, so that

we can assume that they fall through the two-phase region with constant velocity dz/dt.

Calling the difference in density between atomic helium and liquid metallic hydrogen ρ,

the mass settling rate is given by (note that we take the absolute value of dz, as we just seek

a mass-flow rate):

=4πr

ρ

=4π

(

)

ρ

, (2.65)

where r is some average radius, r

<r<r

. This could be the center of mass of the two-

phase layer, but if the layer is thin we can take r = (r

)/2. From equations (2.64) and

(2.65) we can calculate the rate of dissipation of gravitational potential energy:

=Φ

=−2πGMRρz



−z



. (2.66)

Because dU

is the loss in gravitational potential energy, the work done by the gravitational

force on the planet is −dU

, and the work done by the system (i.e. the planet) is thus

−(−dU

). We seek the value of dr/dt that is needed to sustain a given planetary heat

flow, dQ/dt, without change in its internal energy (dE/dt = 0). For an average planetary

heat flux q the total heat flow is given by dQ/dt =4πR

q, so that, from the First Law of

Thermodynamics with dE = 0:

=4πR

q, (2.67)

which upon substitution of equation (2.66) yields:

=−

2Rq

GMρz



−z



. (2.68)

Saturn’s heat flux is q ≈−2Wm

−2

(negative because the system loses heat). Part of

this heat loss almost certainly derives from a decrease in internal energy (dE/dt < 0)

that was stored during an early stage of gravitational contraction (Section 2.5). Setting

dE/dt = 0 thus yields a maximum helium sinking rate. According to Stevenson (1982b)

the two-phase region in Saturn extends from z

≈ 0.51 to z

≈ 0.44. Plugging in Saturn’s

mass (5.69 ×10

kg) and mean radius (58 250 km) and assuming ρ = 1000 kg m

−3

and

z =0.47 we get dr/dt ≈4.2×10

−10

−1

≈1.3 cm yr

−1

. This estimate is almost certainly

an upper bound, but it translates to a displacement of the order of the planetary radius over

the age of the Solar System, which is reasonable because the process appears to be still

taking place today. Saturn’s atmosphere is depleted in helium, with a H

/He ratio (29.6 by

weight) that is higher than that in Jupiter’s atmosphere (6.3, data from Lodders & Fegley,

1998). This is qualitatively consistent with helium unmixing as the source of Saturn’s high

internal energy output (Fig. 2.16).

2.7 Tidal dissipation of mechanical energy

Consider two celestial bodies orbiting their common center of mass. We wish to study

the effects of tides on one of them, which we will call the “secondary”, caused by the

104 Energy sources in planetary bodies

∆r=– r

|r|

tidal

Primary’s

center of mass

Secondary

tidal

∆r=+r

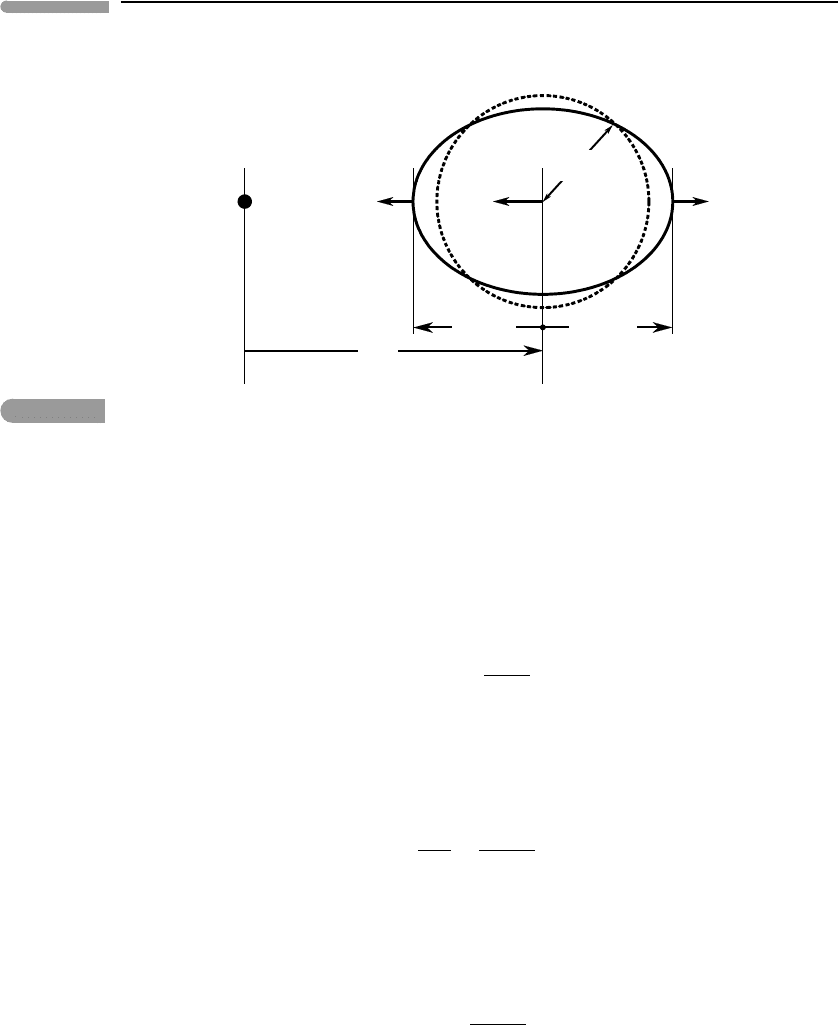
Fig. 2.17

The geometry of tides. Tidal deformation is grossly exaggerated. The secondary’s radius has a magnitude |r |, so that

the distance from the planet’s center to its surface is ±r, as shown.

gravitational pull of the other, which we will call the “primary”. The gravitational force

between the two bodies is given by equation (1.2), with x = R, the distance between

their centers of mass (Fig. 2.17). Real objects have finite extent, so that the gravitational

attraction of the primary varies over the diameter of the secondary, 2r, where in general

r  R. If we call the gravitational acceleration of the primary g

its mass M

we have

from equation (1.7):

=−

, (2.69)

where the negative sign expresses the fact that gravitational force is an attractive force. For

example, if R is positive towards the right, then g

, which points towards the left, must be

negative (Fig. 2.17). This is the gravitational acceleration at the location of the center of

mass of the secondary, but not at its surface. The change in g

with R is given by:

2GM

. (2.70)

Because the secondary’s radius is much smaller than the distance between the objects any

distance r of order r is equivalent to a very small but finite change in R. We call the small

but finite change in gravitational acceleration over this distance the tidal acceleration,

tidal

, i.e.:

tidal

≈

2GM

r. (2.71)

At the point on the surface of the secondary located closest to the primary r =−r (because

we are moving towards the primary), so g

tidal

is negative, i.e. directed towards the primary.

Conversely, at the point furthest away from the primary, r =+r and in this case g

tidal

is positive and directed away from the primary. As a result of these tidal accelerations the

surface of the secondary is subject to tidal forces that, unless the body is perfectly rigid,

give rise to two tidal bulges on opposite sides of the planet, as shown in Fig. 2.17.On

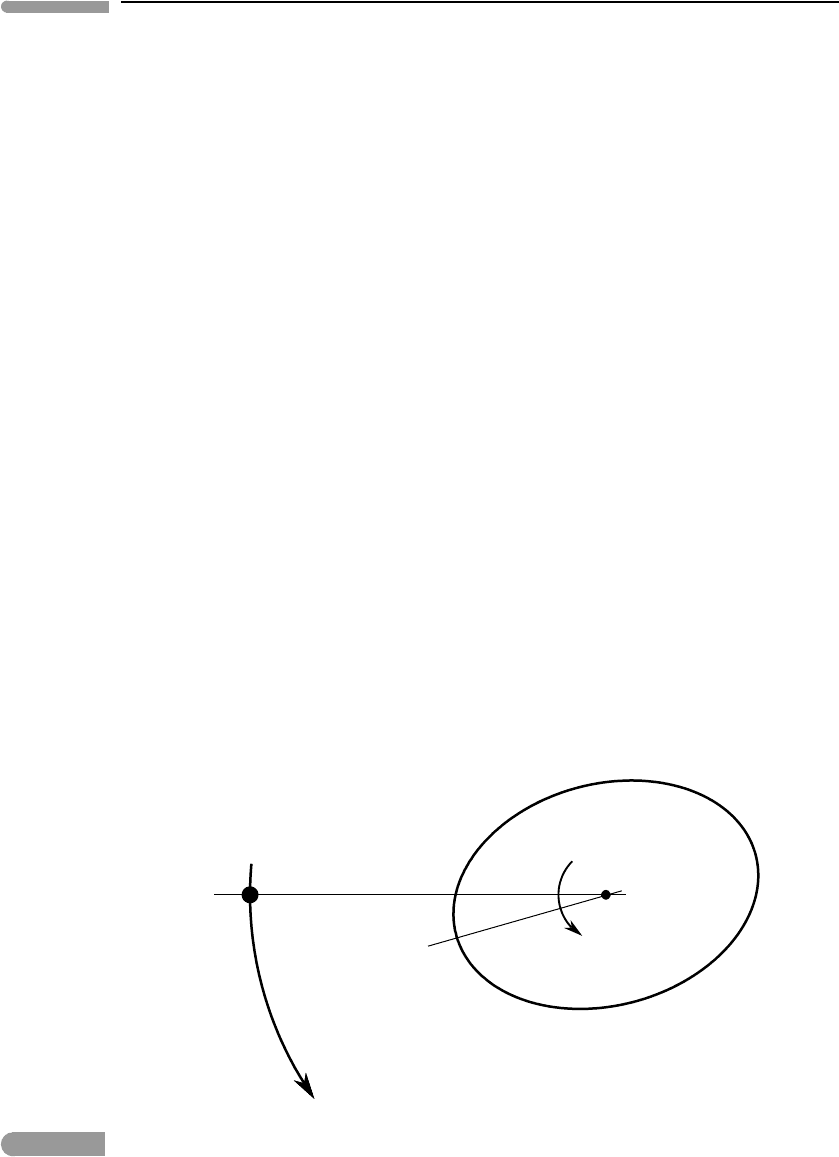
105 2.7 Tidal dissipation of mechanical energy

the two points on the planet’s surface located at 90 degrees from the tidal bulges the tidal

force is directed towards the planet’s center. This result is not included in equation (2.71)

because this is a one-dimensional equation, but it follows immediately from the generalized

three-dimensional version of the equation.

If the relative positions of the primary and secondary are fixed, i.e. if the periods of rotation

and revolution are the same and if the distance between the two bodies remains fixed, then

the tidal deformation of the secondary is constant and there is no energy dissipation. If

any of these conditions is relaxed, however, tidal deformation will change with time. Tidal

flexing then performs work against frictional forces in the planet’s interior, resulting in

energy dissipation. The planet heats up as it constantly stretches and squashes.

Consider for instance the case in which rotation of the secondary is faster than revolution

of the primary – an example of this situation is motion of the Moon (primary) around

the Earth (secondary). The tidal bulge travels over the surface of the Earth as it rotates.

If the planet were made up of a perfectly inviscid material (i.e. with no internal friction)

then there would be no energy dissipation and, moreover, the tidal bulge would always be

exactly aligned with the primary. In reality planets are composed of materials with finite

(and commonly large) viscosities. Raising of the tidal bulge takes a finite amount of time,

and as a result the tidal bulge is located ahead of the point on the secondary that lies directly

below the primary, or in other words at a point that corresponds to an earlier position of the

primary, as shown in Fig. 2.18. Because in this case there is internal friction, as the tidal

bulge moves over the surface of the planet it performs viscous work, which dissipates kinetic

energy of rotation. Angular momentum, however, is conserved, so it must be transferred

from the secondary to the primary (if you have trouble visualizing how this happens, note

that because the tidal bulge is ahead of the primary it exerts on it a gravitational force

that accelerates the primary on its orbit). Over geologic time, the length of the Earth’s day

increases and the Moon moves faster in its orbit and hence moves away from the Earth. The

Primary’s

center of mass

Secondary

rotation

revolution

Fig. 2.18

Tidal lag in a body with ﬁnite viscosity. The secondary’s period of rotation (2π/ω

rotation

) is shorter than the primary’s

period of revolution (2π/ω

revolution

). The tidal bulge peaks at a point that was located below the primary at an earlier

time. The angle δ, greatly exaggerated in the ﬁgure, depends on the material properties of the satellite. No scale.

106 Energy sources in planetary bodies

rotation of the secondary is eventually slowed to become synchronized, or tidally locked,

with revolution of the primary. The tidal bulge is now fixed on the surface of the secondary

and tidal dissipation due to the secondary’s rotation ends. The time needed to achieve

tidal locking is called the characteristic time for tidal despinning (Kaula, 1964; Hubbard,

1984). For the Earth as secondary and the Moon as primary it is of the order of 10

years,

which explains why the Earth’s day is still much shorter than its month, although it has

lengthened from about 10 hours in the Archean to the current 24 hours. If we consider the

Moon as secondary to the Earth as primary the despinning time is of the order of 10

years,

which means that the Moon’s rotation became tidally locked to the Earth very soon after its

accretion. The tidal despinning times for the major satellites of the giant planets are much

shorter, probably on the order of 10

years.

For our purposes there are two important points here. First, when a secondary becomes

tidally locked to its primary tidal dissipation from rotation does not take place. At present

there is no rotationally induced tidal heating of the Moon but there is a small amount of

tidal heating of the Earth. This is, however, insignificant because of the relatively small

mass of the Moon, which gives rise to small tidal forces (equation (2.71)). Second, if tidal

despinning of the Moon and of the satellites of the giant planets was fast enough, it is

possible that they underwent major, but transient, tidal heating events very early in their

histories.

If rotation of a secondary is tidally locked to its primary tidal heating is still possible, as

long as orbital motion is eccentric. Tidal force varies inversely with the cube of the orbital

radius (equation (2.71)) so that as the secondary’s distance to the primary changes along

an eccentric orbit the tidal bulge grows and shrinks and energy dissipation takes place. The

three innermost Jovian satellites, Io, Europa and Ganymede, are locked into orbits with

resonant periods in the ratios 1:2:4. This causes their orbits to be eccentric, which could

cause potentially important tidal heating in the satellites.

Calculation of the amount of energy dissipated by tidal flexing requires detailed knowl-

edge of the planet’s internal structure, chemical composition and physical conditions, and

is far from trivial (see Hubbard, 1984, for a detailed discussion). It is possible, however,

to derive a simplified equation that contains the essential physics of tidal heating and that

yields order of magnitude estimates for the expected energy output. Let the rate at which

tidal energy is dissipated by performing work on a planet be dW

tidal

/dt. The work per-

formed by the planet is the negative of this value, so that the rate at which internal energy

is added to the planet is dE/dt = dW

tidal

/dt (equation (1.55)). On physical grounds we

can expect that dW

tidal

/dt must vary directly with: the rate of change of the tidal force,

the amount of energy that is stored by tidal deformation in response to the changing tidal

force, and the magnitude of the dissipative frictional force. We can express these statements

algebraically as follows:

tidal

=ω

s,o

. (2.72)

In this equation ω is the rate of change of the tidal perturbation and U

s,o

is the amount

of elastic energy stored by tidal deformation. Clearly, the more elastic energy that can

be stored, the more energy will be available for dissipation. If the planet were perfectly

elastic, however, this elastic energy would constantly travel with the tidal bulge but no

energy dissipation would take place. This would be the case if the material that makes up

the planet were inviscid, i.e if it had no internal friction. In reality this is not the case and

we account for the behavior of real planetary materials with the dimensionless parameter

107 2.7 Tidal dissipation of mechanical energy

, called the planet’s dissipation factor. For an inviscid material Q

=∞, and there

is no tidal heating, regardless of how much elastic energy is stored. Materials with high

internal friction are characterized by small values of the dissipation factor and can thus give

rise to high rates of tidal heating. Note very carefully that there is an important difference

between the capability of a material for storing elastic energy, ultimately determined by

its elastic modulus (equation (1.37)), versus how much energy is dissipated when storing

or releasing elastic energy. The latter is a function of the material’s internal friction, or

viscosity, which in turn depends on several variables, including temperature and the rate at

which elastic deformation proceeds. In general, the dissipation factor cannot be calculated

from first principles and must be approximated on the basis of the known or inferred internal

structure of the planet, including its chemical and physical layering and thermal gradient.

We recall that there are two separate components of tidal heating, one due to rotation

(which vanishes if the secondary is tidally locked) and the other one due to orbital eccen-

tricity (which vanishes if orbital motion is circular). We can then break down the tidal work

as follows:

tidal

tidal,r

tidal,e

. (2.73)

We seek the equations that describe each of these components, tidal dissipation by rotation

(dW

tidal,r

/dt) and tidal dissipation due to eccentricity (dW

tidal,e

/dt).

The elastic energy stored per unit volume by tidally induced shear deformation is given

approximately by:

µε

, where µ is the effective shear modulus of the planet, and ε is the

strain caused by the tidal forces (equation (1.37)). The elastic energy per unit mass is then

given by:

s,o

≈

µε

. (2.74)

If tidal forces cause the radius of the planet to change by an amount δr  r, then we can

approximate the strain as ε ≈δr/r. We now seek to relate δr to the secondary’s gravitational

attraction, which resists deformation, and to the tidal effect of the primary, which drives

deformation. Gravitational acceleration is the gravitational potential gradient (equation

(1.9)), so we can write the gravitational potential due to tidal acceleration at the surface of

the secondary as:

tidal

≈

. (2.75)

Note that the derivative of (2.75) relative to r is (2.71). The ratio between gravitational

potential and gravitational acceleration has dimension of length. Thus, on dimensional

grounds (see Box 1.2) we can write:

δr ∝

tidal

, (2.76)

where g

is the gravitational acceleration due to the secondary. The size of the tidal bulge

must vary directly with the ratio between the tidal effect of the primary (Φ

tidal

) and the

secondary’s own gravitational acceleration, g

, so this equation is reasonable on physical

grounds too. We can then define a non-dimensional parameter, h, such that:

δr = h

tidal

. (2.77)