Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

88 Energy sources in planetary bodies

10 100 1000

Impactor radius - km

Maximum kinetic energy dissipated per unit mass - J Kg

–1

100 K

1000 K

10000 K

10 K

100 K

1000 K

10 K

Potential T

Chondrite

Ice

Complete melting possible

Ice

Chondrite

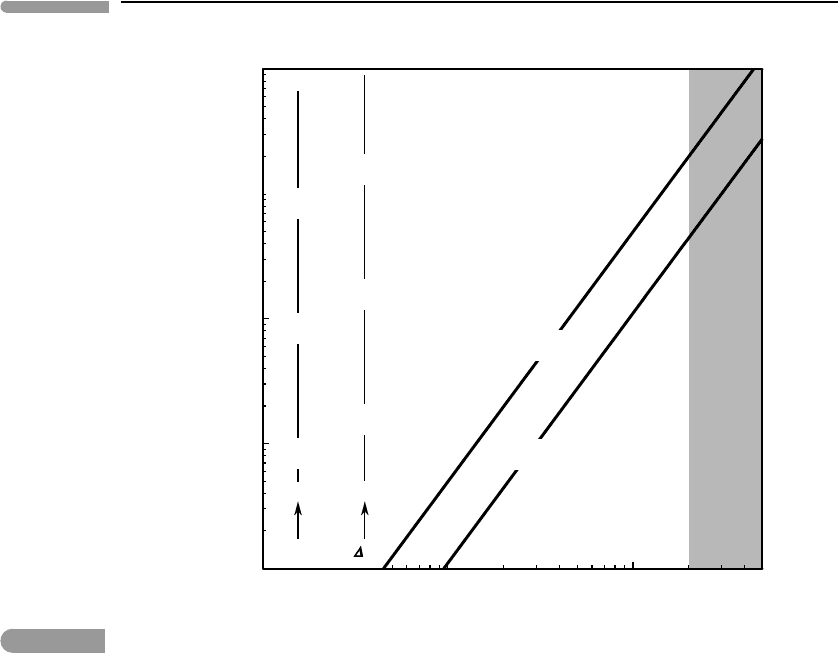
Fig. 2.10

Maximum kinetic energy dissipated per unit mass during inelastic collisions as a function of impactor radius. Values

correspond to collision of two identical bodies of the given radius. The temperature scales show how these energies

would convert to sensible heat in chondritic and ice bodies. Global melting requires energy dissipation of between

5 ×10

and 2 ×10

Jkg

−1

In order for the merged body that results from an inelastic collision to become completely

molten we can specify that the temperature increase must be of the order of 100 K (for

ice bodies) to a few 1000 K (for rock and metal bodies). We then need to add the specific

enthalpies of melting,which are of the order of 3.4×10

Jkg

−1

and 5×10

Jkg

−1

for ice and

rock–metal mixtures, respectively.The result is that a collision between chondritic impactors

must dissipate ∼2×10

Jkg

−1

in order for the resulting body to become completely molten,

whereas complete melting of an ice body requires some 5×10

Jkg

−1

. Figure 2.10 shows

that for both types of materials the minimum impactor radius that produces complete melting

is ∼2000 km.

The global thermal effects of collisions are generally less severe than what one is perhaps

prone to imagine on the basis of the unavoidably catastrophic local effects. This changes

as the colliding bodies approach planetary size (∼2000 km), so that the very last stages

of planetary accretion may have had global thermal consequences (see Wetherill, 1985).

The hypothesis for the formation of the Moon that best fits geochemical, geophysical and

astrophysical evidence is that it was the result of a collision between a Mars-sized body

and the proto-Earth (Hartmann & Davis, 1975; Cameron & Benz, 1991). Such a collision

would have dissipated more than enough energy to completely melt the Earth–Moon system

(Fig. 2.10).

89 2.5 Contraction

2.5 Contraction

We define contraction as a constant-mass process in which the initial lengthscale of the

contracting body may take a finite value (it differs from accretion in both of these respects).

By equation (2.7), contraction (R < 0) at constant mass lowers gravitational binding

energy (increases its absolute magnitude). We seek the relationship between the change in

gravitational binding energy and the change in the body’s internal energy content.

Consider a spherical shell in the interior of a planet, of infinitesimal thickness dr. Take a

sector of this shell of unit cross-sectional area.The difference in pressure between the bottom

and the top of the shell is given by dP =−gdm, where dmis the mass of the infinitesimally

thick sector of unit cross-sectional area, and the negative sign arises because, if r>0 moving

outwards then g points in the negative direction (see equation (1.7)). Now dm=ρdr, which

leads to the following relationship, known as the condition of hydrostatic equilibrium:

=−gρ =−

ρ, (2.34)

where m is the planetary mass contained inside a sphere of radius r (see Box 2.1). The

density, ρ, is in general a function of pressure and temperature, both of which vary with r.

Box 2.1

Gravitational potential of a solid sphere

The gravitational potential of spherical bodies turns up in many calculations of gravitational heating. In order

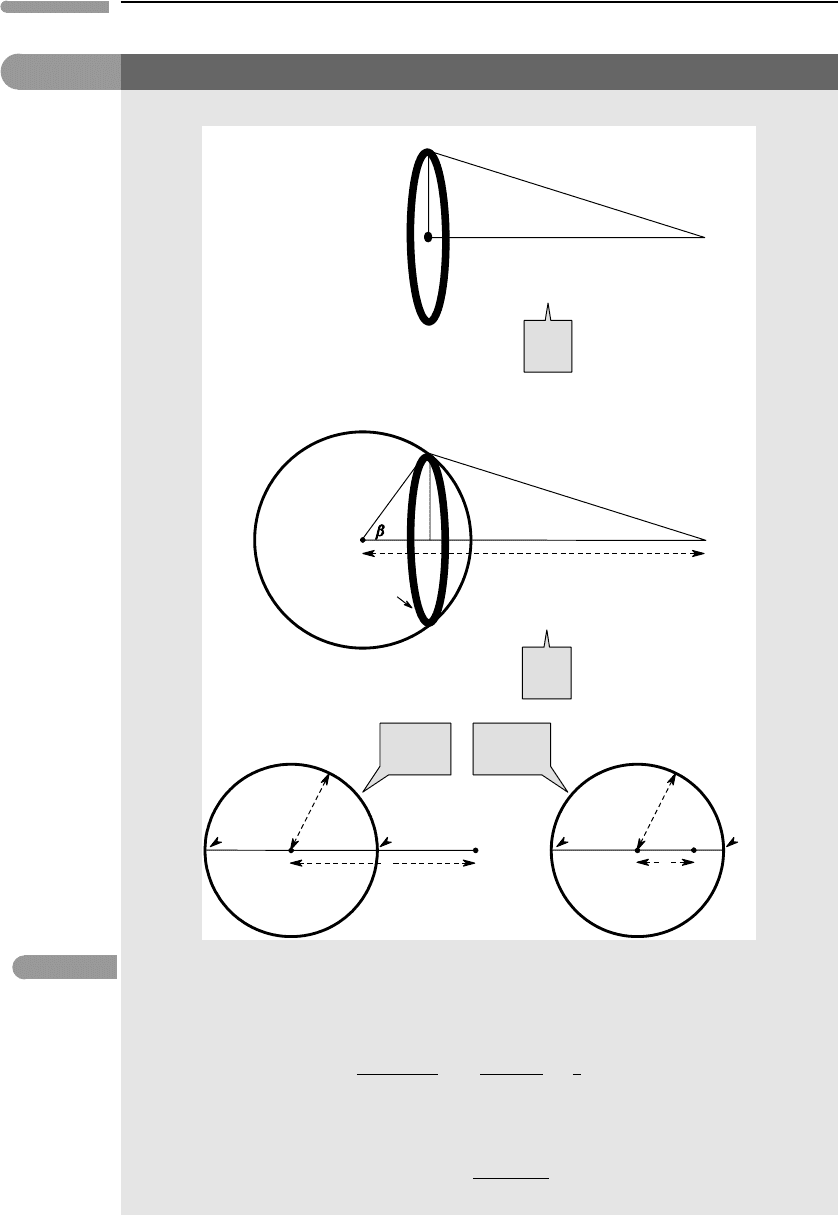
to derive the fundamental equations it is necessary to calculate: (a) the gravitational potential of a ring, (b)

the gravitational potential of a spherical shell (seen as an assemblage of inﬁnitesimal rings – see Fig. 2.11)

and, ﬁnally, (c) the gravitational potential of a sphere, which is an assemblage of inﬁnitesimal shells (Figure

2.12).

(a) Consider a ring of radius a and a point P at a distance r along the ring’s axis. The distance from P to an

inﬁnitesimal element of a ring of mass dm is x. The gravitational potential at P due to this mass element is:

dΦ =−

dm. (2.1.1)

Given the symmetry of the problem x is constant (Fig. 2.11), so the gravitational potential of the entire ring

must be:

Φ =−



dm =−

=−





, (2.1.2)

where M is the mass of the ring. As an exercise, show (i) that the gravitational acceleration vanishes at the

ring’s center (r = 0) but the gravitational potential does not and (ii) that the gravitational acceleration far

away from the ring (r →∞) is equivalent to the gravitational acceleration of a point mass located at the

ring’s center – see equation (1.11).

(b) A spherical shell is an assemblage of inﬁnitesimally thin rings (Fig. 2.11). Now, r is the distance

between P and the center of the spherical shell, and a is the radius of the shell. The radius of the rings is,

z =a sinβ, and x is the distance between a ring element and P, as before. Let dx =adβ be the width of the

ring, and M the mass of the shell. The mass of the ring, dm, is given by the ratio between its surface area and

90 Energy sources in planetary bodies

Box 2.1

Continued

r–a

r+a

a–r

r+a

b(i)

b(ii)

Fig. 2.11 Gravitational potential of a ring (a) and a spherical shell (b), at points outside (b(i)) and inside (b(ii)) the shell.

that of the shell:

dm =

2πa sinβdx

4π a

M =

M sinβdx

M sinβdβ (2.1.3)

and, from equation (2.1.2), the gravitational potential caused by the ring at P is:

dΦ =−

GM sinβdβ

. (2.1.4)

91 2.5 Contraction

Box 2.1

Continued

Fig. 2.12 Gravitational potential inside a solid sphere.

From the law of cosines:

−2ar cosβ. (2.1.5)

Differentiating (2.1.5) and solving for sinβdβ:

sinβdβ =

xdx

(2.1.6)

and substituting in (2.1.4):

dΦ =−

2ar

dx. (2.1.7)

We now need to decide on the integration limits, and these are different depending on whether P is located

inside or outside the spherical shell (Fig. 2.11). For P outside the shell, case b(i), the gravitational potential is

given by:

Φ =−

2ar



r+a

r−a

dx =−

, (2.1.8)

92 Energy sources in planetary bodies

Box 2.1

Continued

which is the same as that caused by a point mass located at the center of the shell. At a point P inside the

shell, case b(ii):

Φ =−

2ar



r+a

a−r

dx =−

. (2.1.9)

Thus, the gravitational potential anywhere inside a spherical shell is constant, and equal to the potential at

the surface of the shell (set r = a in equation (2.1.8)). What is the gravitational acceleration everywhere

inside a spherical shell?

the gravitational potential of each inﬁnitesimal shell of mass dm is given by equation (2.1.8):

dΦ =−

Gdm

(2.1.10)

so the gravitational potential of the sphere of mass M is simply:

Φ =−



dm =−

, (2.1.11)

i.e. the same as that of a point mass located at the center of the sphere. We now seek the gravitational

potential at a point P inside a solid sphere of radius a, located at a distance r from the center of the sphere,

Fig. 2.12. The gravitational potential at P equals the sum of the gravitational potential of the sphere interior

to P, Φ

inside

plus that of the spherical shell exterior to P, Φ

outside

. From (2.1.11), we have:

inside

=−

inside

=−





=−

GMr

. (2.1.12)

The external (ﬁnite) shell is an assemblage of inﬁnitesimal shells, each of them of thickness dx and (variable)

radius x – see Fig. 2.12. The mass of each shell is given by:

dm =

4π x

πa

M =

dx (2.1.13)

and its gravitational potential by equation (2.1.9):

dΦ =−





=−

3GM

xdx. (2.1.14)

The gravitational potential of the shell external to P is, then:

external

=−

3GM



xdx =−

3GM



−r



(2.1.15)

so that the gravitational potential at P, Φ = Φ

inside

+Φ

outside

is:

Φ =−



−r



. (2.1.16)

As a ﬁnal exercise, prove that the gravitational acceleration at P is derived only from the mass internal to P,

i.e. from the sphere of radius r in Fig. 2.12. Newton was the ﬁrst one to prove this (oh, by the way, he had to

come up with calculus in the process).

93 2.5 Contraction

Planetary radius changes during contraction so it is more convenient to choose mass as the

independent variable and write our equations in terms of infinitesimal mass increments,

dm. In this way the integrals that describe the planetary interior are always taken between

zero, at the planet’s center, and the total (constant) planetary mass M at the planet’s surface.

From equation (2.5) we obtain:

4πr

(2.35)

and, by the chain rule:

=−

4πr

. (2.36)

Mass increments dm are positive outwards (i.e. towards the planet’s surface) and this

equation states that pressure decreases in the same direction, as expected. Equation (2.36)

was derived exclusively from the condition of hydrostatic equilibrium, but its right-hand

side contains the factor Gm/r, which is the integrand in the equation for gravitational bind-

ing energy (equation (2.4)). Multiplying the right-hand side of equation (2.36)by4πr

and

integrating over the planetary mass we obtain:

−



4πr

dm =−



dm =U

. (2.37)

Applying the same operations to the left-hand side of equation (2.36) yields the expression:



4πr

dm, (2.38)

which can be integrated by parts. By the chain rule:



4πr



=12πr

(2.39)

so that:



4πr

dm =



4πr



−



12πr

dm. (2.40)

The first term on the right-hand side of this equation vanishes, because at the planet’s center

(m = 0) it is r = 0, and at the planet’s surface (m = M)itisP = 0. Using equation (2.35)

to eliminate dr/dm from the integrand in the second term we get:



4πr

dm =−



12πr

4πr

dm =−3



dm (2.41)

which, by using (2.36) and (2.37), yields:

=−3



dm. (2.42)

This is a fundamental result. It states that, in a self-gravitating body at hydrostatic equi-

librium, the gravitational binding energy and the body’s thermodynamic state are not

independent variables. Both pressure and density are thermodynamic state variables that

94 Energy sources in planetary bodies

are related to temperature, and hence to internal energy, by an equation of state. It is thus

always possible, at least in principle, to relate the body’s gravitational binding energy,

, to its internal energy, E. A special case of this result, known as the virial theorem

(Worked Example 2.3) was first derived by Clausius in the 1850s. Equation (2.42)

is applicable to the formation of celestial bodies, including planets, stars, gravitationally

bound star clusters and even galaxies, provided that they evolve by contraction at a rate such

that hydrostatic equilibrium is maintained throughout the entire process. If this is the case

then equation (2.42) determines how much of the gravitational binding energy dissipated

during contraction becomes internal energy and how much becomes thermal radiation that

is lost to space. This result does not apply to accretion, which is a non-equilibrium process.

Worked Example 2.3 Thermal evolution of a contracting self-gravitating sphere of ideal gas

In order to calculate the relationship between gravitational binding energy and internal

energy it is necessary to use an equation of state to express the ratio P/ρ as a function of E.

This is very straightforward for an ideal gas, but is the ideal gas equation of state applicable

to any type of celestial bodies? It turns out that P –T conditions in many low mass stars

and proto-stellar clouds are such that the ideal gas equation of state is indeed a very good

description of their material properties, because the characteristic energy of particle interac-

tions is negligible compared to their thermal energy (Section 1.15). The fully ionized matter

inside a star with mass comparable to that of the Sun behaves likes a monatomic ideal gas.

The density of the gas is given by ρ = w/V , where w is its molecular weight (proper

mass!) and V the molar volume. We then have:

. (2.43)

From Section 1.14.2 we see that the molar internal energy of an ideal gas is given by:

E =

RT (2.44)

and its molar heat capacities by:

R; C

f +2

R, (2.45)

where f is the number of translational +rotational degrees of freedom of the gas molecules.

The ratio of the heat capacities is a variable that occurs often in thermodynamics so it is

given its own symbol, γ, which for ideal gases is:

γ =

=1 +

(2.46)

from which it follows that:

RT =

(

γ −1

)

E. (2.47)

Substituting in (2.43) and then in (2.42) we arrive at:

=−3



dm =−3

(

γ −1

)



edm, (2.48)

95 2.5 Contraction

where e = E/w is the internal energy per unit mass. The integral is taken over the entire

mass of the body, so that even though e may vary for each mass increment, the value of the

integral is simply E, the total internal energy content of the self-gravitating body of ideal

gas. We thus arrive at the following simple yet very powerful result, which is known as the

virial theorem (see the classic textbook by Chandrasekhar, 1958, for a beautifully elegant

alternative derivation):

=−3

(

γ −1

)

E. (2.49)

Any self-gravitating body of ideal gas at hydrostatic and thermodynamic equilibrium must

follow this relationship between its gravitational binding energy and its total internal energy.

The change in gravitational binding energy during contraction (U

< 0) equals

the mechanical work performed by the planet (Exercise 2.5) so that the First Law of

Thermodynamics applied to a contracting planet can be written as follows:

dE =dQ −dU

, (2.50)

which, rearranging and substituting equation (2.49), becomes:

dQ =dE −3

(

γ −1

)

dE =

(

4 −3γ

)

dE. (2.51)

There is a strict relationship between the heat exchanged by the body, dQ, the change

in its internal energy, dE, and the change in its gravitational binding energy, dU

. For a

monatomic ideal gas we have γ = 5/3, so that in this case:

dQ =−dE =

. (2.52)

This is a remarkable result. If a self-gravitating body of monatomic ideal gas radiates energy

to space (dQ < 0), then it must contract. The gravitational potential energy dissipated by

this contraction (dU

< 0) is split into two equal parts. One half balances the radiated

energy and the other half becomes internal energy (dE > 0). As the surface of the body

radiates heat to space the temperature in its interior increases. This process is called Kelvin–

Helmholtz cooling and is responsible for heating proto-stars to the temperatures needed to

ignite thermonuclear fusion reactions in their cores.

It is important to realize that this specific result (equation (2.52)) rests on the assumption

that the self-gravitating body is composed of monatomic ideal gas, which is an excellent

approximation to the behavior of hot proto-stars (see Section 1.15) but not, for example, of

cold fluid planets. Consider for the sake of argument a cold body made up of polyatomic

molecules with translational + rotational six degrees of freedom, for which γ =4/3. In this

case:

dQ =0, −dE = dU

. (2.53)

Such a body would not radiate any of the gravitational potential energy that would be dis-

sipated during contraction. Of course, if the surface temperature of the body is above 2.7 K

(Chapter 13) then it will radiate heat to space and contract, but in this case all of the grav-

itational potential energy that is dissipated goes to raising the body’s internal temperature.

We will examine this topic again in Chapter 9, in the context of equations of state for fluid

planets.

96 Energy sources in planetary bodies

Kelvin–Helmholtz contraction may have been responsible for some fraction of the initial

internal energy budgets of the gas and ice giants, but their present day thermodynamic

states make this mechanism largely inoperable (Chapter 9). Contraction ceased, probably

shortly after formation of the Solar System, when the planets reached density–temperature

conditions such that the energies of particle interactions were no longer negligible compared

to their thermal energies, and the planetary matter condensed. Present-day heat flows of the

fluid planets are thought to derive largely from slow escape of the internal energy stored

during the early stage of contraction, although ongoing differentiation may be a significant

additional heat source in some of them (Hubbard, 1970, 1980; Flasar, 1973; Graboske et al.,

1975; Stevenson, 1982b; Guillot, 2005).

2.6 Differentiation

Differentiation of a homogeneous planet releases gravitational potential energy, as the

denser material sinks in the planet’s gravitational field to form its core. Because dissi-

pation of mechanical energy takes place deep within the planet, core formation could be a

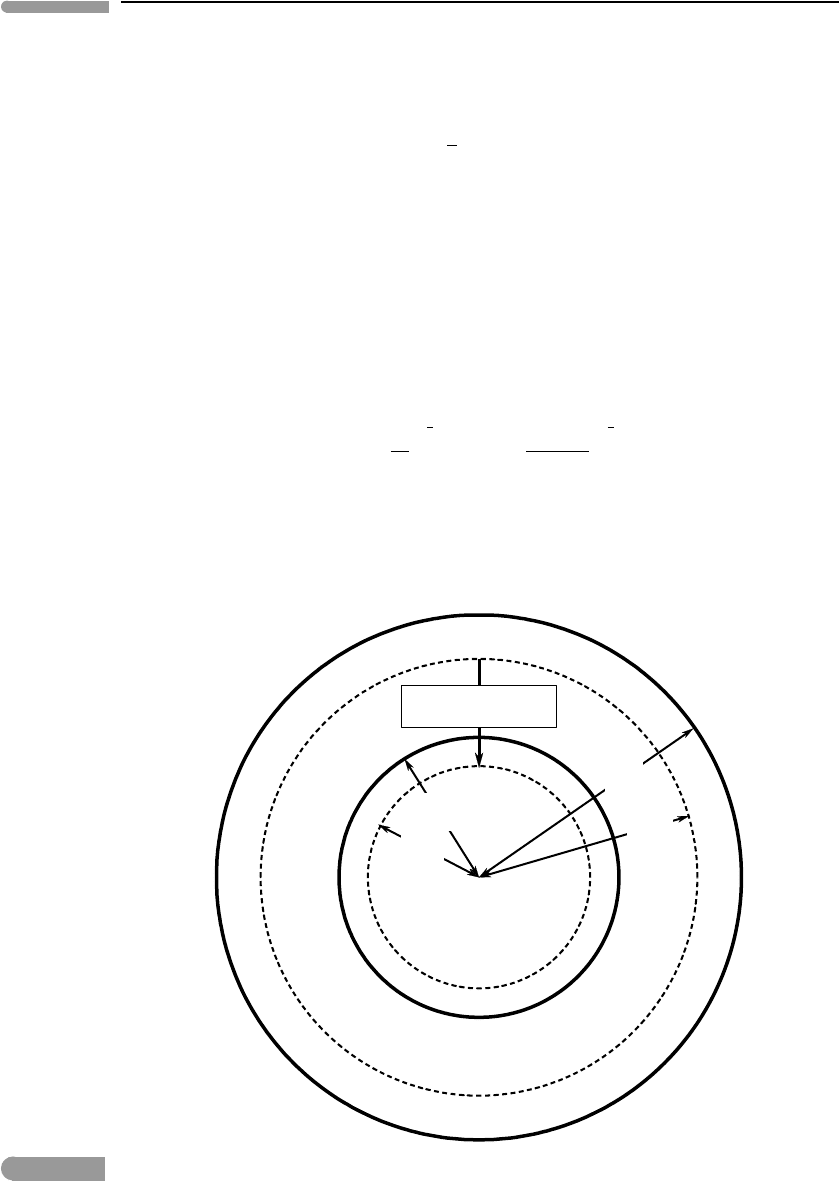
particularly efficient mechanism for raising a planet’s internal energy content. Consider an

undifferentiated planet of radius R and homogeneous density ρ

. The planet then differen-

tiates into a core of radius r and density ρ

, sheathed by a mantle of density ρ

extending

from r to the planet’s surface at R (Fig. 2.13). From mass balance we obtain the following

relationship between core radius and planetary radius:



−ρ



. (2.54)

We can visualize the core-forming process as follows. Assume that the undifferentiated

planet is composed of infinitesimal volume elements that can have a density of either ρ

. These elements are initially distributed homogeneously throughout the entire planet,

in a proportion that yields a mean density ρ

. Let x be the distance of an arbitrary volume

element from the planet’s center. During core formation, all volume elements of density ρ

located at x>rexchange places with elements of density ρ

located at x<r. The result

of this process is a core or radius r made up of all volume elements of density ρ

and a

Fig. 2.13

Differentiation of a planet with initial homogeneous density ρ

into a core with density ρ

and a mantle of

density ρ

97 2.6 Differentiation

mantle that comprises all elements of density ρ

. The total mass added to the core is then

given by:

m

πr

(

−ρ

)

. (2.55)

The loss in gravitational potential energy of this mass is the amount of mechanical energy

dissipated by core formation, and hence the increase in the planet’s internal energy, assum-

ing for now that none of it is radiated to space. Each volume element undergoes a different

displacement, ranging from R (for an element falling from the planet’s surface to its cen-

ter) to 0 (for an element initially located at r). A characteristic displacement during core

formation is thus given by the distance between the center of mass of the mantle, r

, and

the center of mass of the core, r

. The radii r

and r

are defined as the distances from the

planet’s center such that half of the mantle’s mass, and half of the core’s mass, are located

inside r

and r

, respectively (Fig. 2.14). From mass balance we find:





; r





. (2.56)

A reasonable estimate of the amount of mechanical energy dissipated by core formation is

then given by the change in the gravitational potential energy, U

, of a mass equal to the

mass added to the core, m

, falling from r

to r

Characteristic

mass displacement

Fig. 2.14

During differentiation, a typical volume element of core material falls from the center of mass of the mantle at r

the center of mass of the core at r

, exchanging places with a volume element of mantle material.