Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

118 Energy sources in planetary bodies

(Scott, 2007). The values of C

for the extinct radionuclides are simply the product of these

initial isotopic abundances by the corresponding elemental abundances.

We now seek an order of magnitude estimate of the contribution of radioactive decay to

present-day terrestrial heat output. This requires knowledge of the Earth’s bulk chemical

composition, on which there are considerable uncertainties. Estimates of the bulk composi-

tion of the Earth are based upon the compositions of chondritic meteorites, complemented

by a number of inferences and reasonable assumptions. We know, for example, that the Earth

is depleted in volatile elements relative to chondritic meteorites, including in potassium,

which is a moderately volatile element. Starting from the present-day bulk earth elemental

abundances given by Kargel and Lewis (1993) we use equations (2.98) and (2.97) and the

data in Table 2.2 to calculate the temporal evolution of radioactive heat production in the

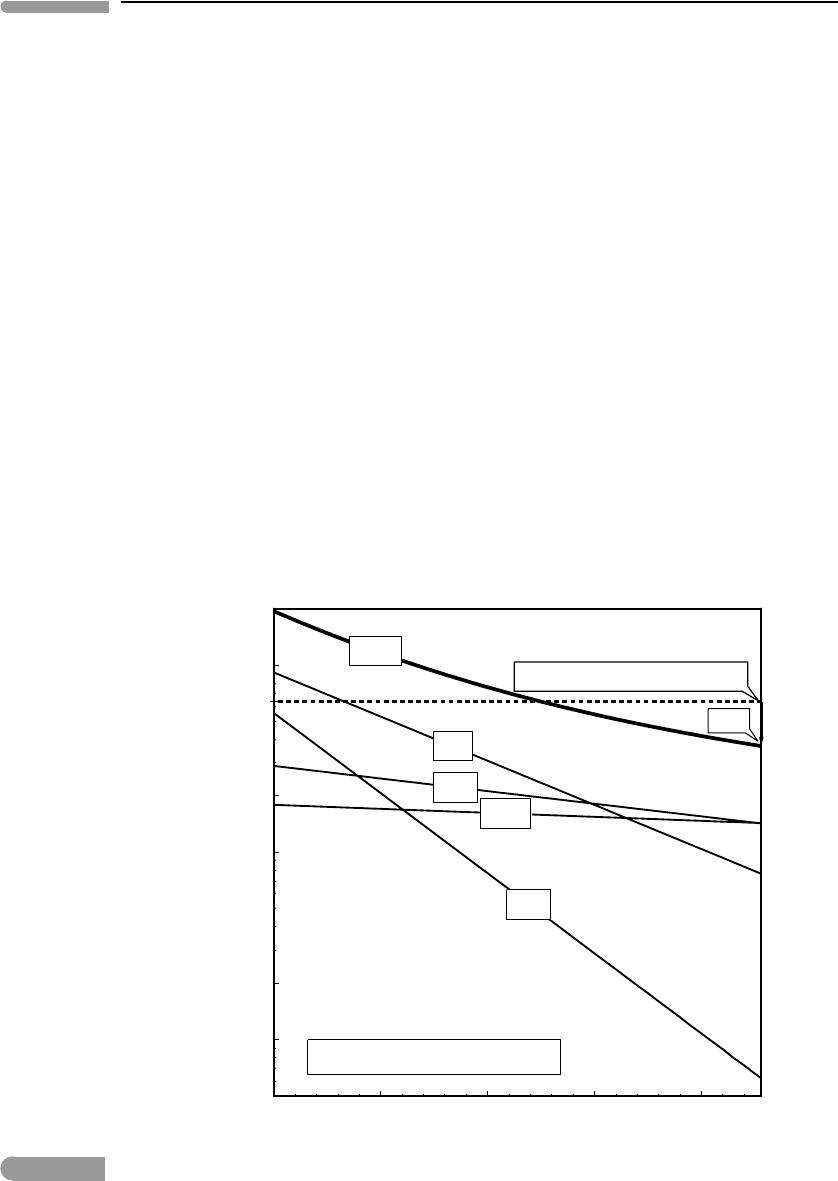
Earth. The results are shown in Fig. 2.21. We can see that at the present time radioactive

heating accounts for about one half of the observed terrestrial heat output. The balance

represents secular cooling, i.e., slow loss of internal energy that was stored during an earlier

epoch. The source of some of this energy may have also been radioactive decay, which

generated considerably more heat in the distant geologic past than today, largely as a result

of significantly higher abundances of

K and

235

U, with half lives of ∼1.3 and 0.7 billion

years, respectively (Fig. 2.21). Much of the Earth’s secular cooling, however, may still

reflect core formation. As we saw in Section 2.6, differentiation of the Earth dissipated

enough gravitational potential energy to melt the whole planet several times over. Given

that result (Worked Example 2.4) and the temporal evolution of radioactive heat production

–13

–12

–11

Time after formation of the Solar System (Ga)

Radioactive heat production – Wkg

–1

Bulk Earth radioactive heating

Present terrestrial heat output

235

238

232

Total

57%

Fig. 2.21

Temporal evolution of bulk Earth radioactive heating per unit mass. Broken line shows the present-day terrestrial heat

output. Present radioactive heating accounts for about half of this value.

119 2.9 Radioactive heating

shown in Fig. 2.19, it is hard to see how one can avoid the conclusion that terrestrial heat

output during the Archean and Early Proterozoic must have been much higher than today’s.

A refined estimate of the history of terrestrial heat flow requires that we also take into

account the fact that there are strong geochemical controls on the distribution of radioactive

elements, as well as the effects of heat transfer, which we will do in Chapter 3.

A wide range of thermal regimes is known to have affected different early Solar System

objects. For instance, some carbonaceous chondrites may have undergone aqueous alter-

ation at liquid water temperatures, whereas basaltic achondrites and iron meteorites indicate

that some asteroid-sized bodies underwent essentially complete melting. Electromagnetic

induction heating is a possible energy source for thermal processing of early Solar System

objects (Section 2.8), but it is not the only one. Decay of short-lived radionuclides may

have fueled an early but very short phase of extreme heating of planetesimals. Consider

as an example an object with the composition of CI chondrites (this is the group of chon-

dritic meteorites that most closely match the Sun’s composition, except for loss of volatile

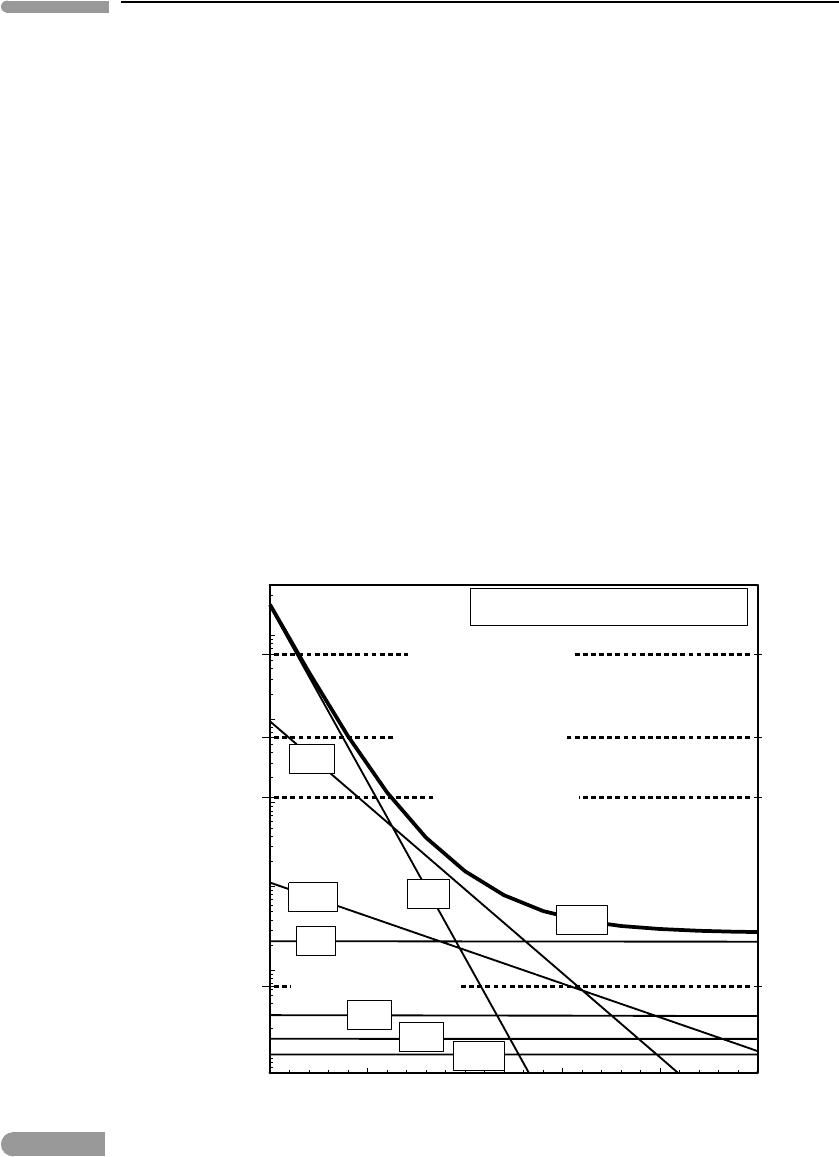
elements). Figure 2.22 shows radioactive heat production in such an object during the first

25 million years after formation of the Solar System, using data from Table 2.2 and chon-

dritic bulk composition from Palme and Beer (1993). Decay of

Al dominates during the

first ∼3 million years, and during that time it generates heat at rates 1–2 orders of magnitude

greater than Io’s present-day extreme heat output. Decay of

Fe is the chief heat source

between ∼6 and ∼13 million years, after which time the long-lived isotopes take over. The

0510 15 20 2

–12

–11

–10

–9

–8

–7

Time after formation of the Solar System (10

yr)

Radioactive heat production – Wkg

–1

CI chondrite radioactive heating

Earth’s present heat output

235

238

232

Total

Chondrite melting

in1 m. yr.

Chondrite melting

in 10 m. yr.

lo’s present

heat output

Fig. 2.22

Radioactive heating per unit mass in CI chondrites during the initial 25 million years of the Solar System. The broken

horizontal lines labeled “Chondrite melting” are average heating rates required to melt chondritic material in 1 and 10

million years.

120 Energy sources in planetary bodies

most intriguing observation to come out of Fig. 2.22 is that heat output from decay of

during the first million years may have been several times higher than the average rate of

supply of heat that would have been required to completely melt the chondritic object in 1

million years. This comparison is of course incomplete, as it ignores the effects of heat loss

(Chapter 3), but for a large enough body heat loss over a time scale of 10

years, before it

melts and starts convecting, is negligible. It is hard to see how objects that accreted while

Al was still abundant could have escaped wholesale melting. Why, then, are there chon-

dritic meteorites that presumably come from parent bodies that never underwent melting

temperatures, and in many cases may have been barely heated? The most likely explanation

is that chondritic parent bodies accreted late enough that most short-lived isotopes were well

on their way to becoming extinct, whereas differentiated parent bodies may have been the

first ones to accrete (Bizzarro et al., 2004; Scott, 2007). A question that in my view has not

been satisfactorily answered is how short-lived radioisotope heating explains the thermal

gradient across the asteroid belt (see Section 2.8) and whether electromagnetic induction

heating also played a role in the origin of this gradient.

Exercises for Chapter 2

2.1 Derive equations (2.20), (2.21) and (2.22). Note that in both the linear and exponential

accretion models the accretion rate does not vanish when the planet reaches its final

mass, whereas in the sinusoidal model accretion rate is forced to be zero at the final

planetary mass. Comment on the relative merits of the three models, and discuss which

may be a better representation of the way in which terrestrial planets accrete.

2.2 Use the Maple worksheet accretion to study the effects of emissivity, nebular

temperature, total mass and accretion time on the initial thermal structure of terrestrial

planets. Search the literature for possible thermal gradients in the solar nebula, and

discuss the extent to which the initial thermal structures of Mercury and Mars could

have differed, assuming that they accreted at their present day heliocentric distances.

2.3 Use accretion to study accretion of icy bodies. Explore the effects of lower den-

sity and lower emissivity of ice compared to rock, and of possibly lower nebular

temperatures.

2.4 Derive the equation for escape velocity, V

(see Section 2.4.1), from the definition that

is the speed at which the kinetic energy of a body equals its gravitational potential

energy. Note that V

depends on the distance to the attractor’s center of mass, but the

value is always well defined in the neighborhood of a planet’s surface.

2.5 Show that for a contracting self-gravitating body at hydrostatic equilibrium the change

in gravitational binding energy equals PdV work on the planet.

2.6 The virial theorem describes equilibrium conditions during contraction. In order for

contraction of a self-gravitating cloud of gas to start, however, it must be out of

equilibrium. Its specific gravitational binding energy (e.g. given by equation (2.10))

must be greater than its specific internal energy (Section 1.14). Derive an equation

that yields the minimum density that a gas cloud must have in order for contraction

to start, as a function of its radius and its temperature, assuming that it consists of

monatomic ideal gas. Assume that the Sun formed from a cloud of gas with a diameter

of 10 light years, at an initial temperature of 50 K. What were the density and the

121 Exercises for Chapter 2

mass of the cloud? How does the mass of the cloud compare to the mass of the Sun?

Comment on your results.

2.7 Derive a relationship between the linear contraction rate of a proto-star (dR/dt ) and its

surface temperature, assuming that it contracts at equilibrium and that it is composed

of monatomic ideal gas. Before the discovery of nuclear fusion, one of the explanations

proposed to account for solar radiation was Kelvin–Helmholtz contraction. Estimate

the necessary contraction rate, assuming that the Sun radiates at 6000 K. Comment

on your results.

2.8 Demonstrate that the gravitational acceleration at a point inside a solid sphere is

derived only from the mass contained inside the radius of the point (see Box 2.1).

2.9 Prove to yourself that I did not make any mistakes in the tedious derivation of equation

(2.61). This is good Maple practice.

2.10 Assume that for Mercury µ =5 ×10

Pa, Q

=100 and h = 1. Calculate the likely

magnitude of present-day tidal heating in Mercury from Solar-induced tides. Is this

a plausible energy source for Mercury’s magnetic field? Calculate the possible tidal

heating of Mercury before tidal despinning, assuming that it had a 10-hour day. Com-

pare this value with present-day measured planetary heat flows (e.g. Earth, Moon,

Io). All data needed to solve this problem not listed here can be found in Lodders and

Fegley (1998).

2.11 Assume that for Tritonµ =10

Pa, Q

=100 and h =1. Calculate the likely magnitude

of present-day tidal heating in Triton (all data needed to solve this problem not listed

here can be found in Lodders & Fegley, 1998). Comment on your results, in view of

Triton’s young and active surface features.

2.12 Discuss how the quasi-static accretion model may be affected if short-lived isotopes

such as

Al,

Fe and

Mn are present in the accreted material (it is fairly straightfor-

ward to modify accretion in order to include this effect). Research the literature

to find out what is known about the presence of short-lived isotopes during accretion

of the Earth.

Energy transfer processes in planetary

bodies

We have developed a comprehensive physical description of the processes and pathways

by which planetary bodies acquire internal energy. Our next task is to examine how this

internal energy drives planetary processes. The hallmark of an active planetary body is that

it has surface features, other than impact craters, that have ages that are negligible compared

to the age of the Solar System. This is true for any epoch of the Solar System. For instance,

the youngest features on the Moon, the immense basaltic plains that we call lunar maria, are

about 3 billion years old. This means that the Moon is dead today, but it was active when

the age of the Solar System was of the order of 1.5 billion years

Active planetary processes are associated to heat flow, but the causal connection is

not always the same. Consider the ascent of magmas. This is a process that transfers

mass and heat from the planet’s interior towards its surface, and that is made possible

by melting, which entails conversion of thermal energy to chemical energy. Ascent of

magma and construction of volcanoes, however, are not driven by thermal energy but

by gravitational energy. Magmas rise to the surface of a planet if they are buoyant, and

magmas are buoyant if melting causes a decrease in density. The essence of the process

can be captured by considering a parcel of magma of unit volume and density ρ

, ris-

ing from a depth at which the planetary radius is r to the planet’s surface at radius R

> r, and exchanging places with an equal volume of country rock of density ρ

>ρ

(Fig. 3.1). The process takes place inside a solid sphere (Box 2.1). We neglect energy

dissipation by friction. The change in gravitational potential energy of the magma is

given by:

U

g,m

=−

GMρ



−R



(3.1)

and the change in gravitational potential energy of the country rock by:

U

g,c

=−

GMρ



−r



. (3.2)

The change in gravitational potential energy of the magma ascent process is, therefore:

U

=U

g,m

+U

g,c

(

−ρ

)



−R



< 0. (3.3)

Ascent of magma corresponds to a decrease in gravitational potential energy and, in fact,

it is physically and mathematically indistinguishable from planetary differentiation – the

distinction is one of scale only. But the First Law of Thermodynamics requires that we

122

123 Energy transfer processes in planetary bodies

(a) (b)

Fig. 3.1

Energy aspects of magma ascent. In (a) a batch of magma of density ρ

initially located at radius r exchanges places

with an equal volume of country rock of density ρ

, initially located at the geoid, radius =R. If the magma ascends

no further then there is an “excess” in gravitational potential energy which must be dissipated as heat. In (b) the

magma is allowed to rise until its gain in potential energy balances that lost by the country rock, building a volcano

with center of mass at radius R

account for the gravitational potential energy that is “lost” in equation (3.3). In order to

do so, we must realize that the process depicted in Fig. 3.1a is not the whole story. If

the magma stops at or below the planet’s geoid (say, it forms a shallow intrusion) then

the potential energy that is “missing” in equation (3.3) is dissipated as heat, just as in the

case of planetary differentiation. If the magma is able to rise above the geoid then the

potential energy released by ascent of magma from its source to the geoid becomes the

gravitational potential energy of the magma (i.e. of a volcano) relative to the geoid (Fig.

3.1b). If we neglect frictional losses, the potential energy lost by the sinking country rock

must be balanced by the potential energy gained by the magma in rising from its source to

the volcano’s center of mass (radius R

in Fig. 3.1b).

Volcanism is not possible in the absence of planetary internal energy, but there is no net

conversion of thermal energy to mechanical energy in the process. The thermal energy that

is converted to chemical energy during melting is released as heat during crystallization

and is eventually radiated to space. There is net transfer of mass in a gravitational field, so

that the source of energy for magma ascent is gravity.

Consider now processes such as plate tectonics, atmospheric circulation or planetary

dynamos, which are all manifestations of convection. In contrast to volcanism, in all of

these processes there is conversion of thermal energy to mechanical energy, but there may

not be mass transfer in a gravitational field. This is so because convection is a cyclic process

in which there is no accumulation of mass anywhere on the cycle, at least on time scales

that are long relative to the time of one convective overturn. Convection is not possible in

the absence of a gravitational field, but, since there is no net mass transfer, gravity cannot

be the energy source for convection. Convection is driven by conversion of thermal energy

(either a planet’s internal heat or solar energy) to mechanical energy. There is a remarkable

symmetry here with magma ascent, which is not possible in the absence of internal energy,

but that is not driven by internal energy. The key to this symmetry is whether or not there

is net transfer of mass down a gravitational field. The study of planetary sciences requires

a good physical and mathematical understanding of heat-transfer processes and this is the

goal of this chapter.

124 Energy transfer processes in planetary bodies

3.1 Transport processes

The First Law of Thermodynamics is the mathematical expression of the principle of con-

servation of energy. Two other quantities that are conserved are mass and momentum. Each

of these three conserved quantities is associated with another quantity, which we may call

a potential, such that if there is a potential gradient the conserved quantity will tend to

flow down the potential gradient. This is one possible way of stating the Second Law of

Thermodynamics, as we shall see in greater detail in Chapters 4 and 12. For example, a

temperature gradient drives the flow of internal energy. A gradient in concentration (or,

more accurately, in chemical potential, Chapter 5) causes matter to flow, for example in

an initially inhomogeneous solution or across an osmotic barrier. Transfer of momentum

is more complicated because momentum is a vector quantity, in contrast to energy and

mass that are scalar quantities, but the principles are the same. The mathematical law that

describes the flow of these three conserved quantities is one and the same and can be written

in its most simple form as follows:

f =−c

dΦ

. (3.4)

In this equation f is the flux of the conserved quantity, i.e. the amount of energy, mass or

momentum that is transported per unit of time and per unit of area perpendicular to the

direction of transport. The potential that drives the flow is Φ, so that dΦ/dx is the potential

gradient, and the negative sign expresses the fact that the conserved quantity is transported

down the potential gradient. The parameter c is a material property which for now we will

assume to be a constant, although in general it is a function of temperature and it may also be

a function of dΦ/dx. This latter point can introduce immense computational complications.

We also note that, in its complete mathematical formulation, f is a vector, dΦ/dx is a one-

form, and c is another geometric object called a second-order tensor. In order not to get

bogged down in these mathematical complications we restrict our discussion to transport

in one spatial dimension, in which case all three geometric objects can be thought of as

scalars, as shown in equation (3.4) (in fact, a scalar is a zeroth-order tensor). But one must

always keep in mind that flow and flux (flow per unit area) are vectors.

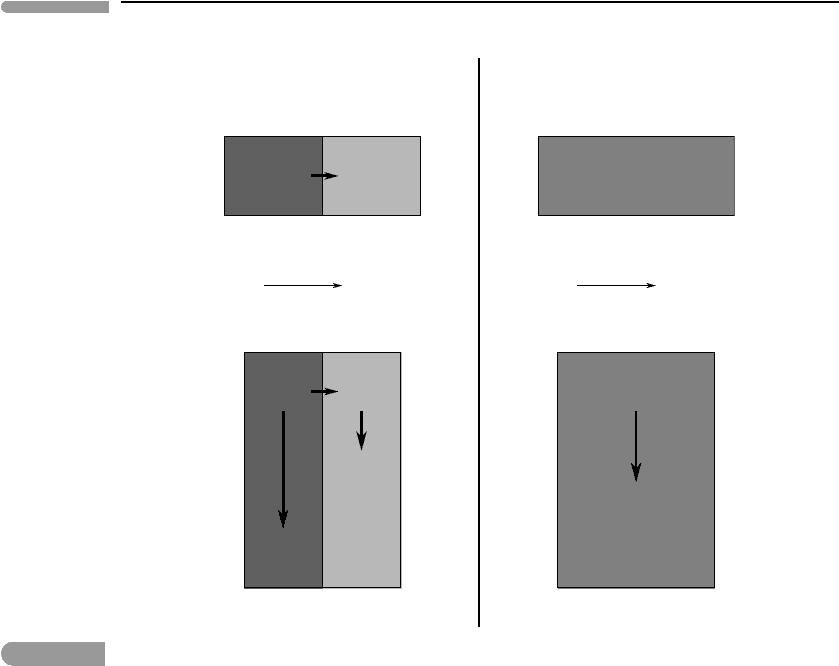
Consider energy conservation first, which is schematized in the drawings at the top

of Fig. 3.2. Temperature is the potential that drives heat flow. If there is a difference in

temperature across a parcel of matter such that T

, then internal energy flows from

the high temperature region towards the low temperature one. The magnitude of the heat

flux, q, is given by:

q =−k

, (3.5)

where k is a material property called thermal conductivity. If we express q in units of

−1

−2

then the units of k are J s

−1

. Because energy is conserved, in the

absence of energy exchanges with the environment the system evolves to a state at a time t

later than t

in which its internal energy, and therefore its temperature T

, are uniform and

such that T

(see Fig. 3.2). Equation (3.5) is also known as Fourier’s law of heat

conduction, in honor of the French scientist Jean Baptiste Joseph Fourier (1768–1830) who

first gave it its mathematical form, and who made many other fundamental contributions

to physics and mathematics. In Fourier’s time it was not realized that equation (3.5)is

125 3.1 Transport processes

x x

> t

Fig. 3.2

Analogy between diffusive transfer of heat down a temperature gradient dT/dx (top panels, where T

> T

) and

transfer of momentum down a velocity gradient du/dx (bottom panels, with u

> u

). Time ﬂows from t

to a

later time t

actually a special case of (3.4). Now it is better to think of equation (3.5) as one of several

constitutive relations, which describe the physical behavior of a material. The behavior that

is described by equation (3.5) is how the material transports heat by diffusion, which is

the macroscopic expression of propagation of kinetic energy among microscopic particles

without bulk macroscopic displacement of matter. Equation (3.5) tells us the rate at which

diffusive heat transfer takes place.

Diffusion of momentum is analogous to diffusion of heat. To see this, consider the draw-

ings at the bottom of Fig. 3.2, which represent flow of a fluid in which there is a velocity

gradient. The fluid flows downwards, as shown by the velocity vectors ¯u

> ¯u

, but the

velocity gradient is in the x direction, which is the direction in which we apply equation

3.4. An important point of this thought experiment is that the boundary of the fluid region

drawn in Fig. 3.2 does not represent a physical boundary, but rather a region within an arbi-

trarily large volume of fluid. In the absence of external forces the momentum inside this

region is conserved, just as internal energy is conserved inside a region which undergoes

neither heat nor work exchanges with its environment. The result is that at a time t

, later

than t

, the velocity will be distributed uniformly across the fluid region, and will have a

magnitude ¯u

, such that ¯u

> ¯u

, see Fig. 3.2. Momentum has been transported from

left to right, driven by the velocity gradient du/dx. One can visualize this process in terms of

126 Energy transfer processes in planetary bodies

infinitesimally thin layers of fluid, which initially move with progressively higher velocities

towards the left. Because of the velocity difference there is a drag force between the layers.

This force transfers momentum from a layer to its neighbor to the right, that moves more

slowly, so that the former layer slows down and the latter speeds up. Momentum is thus

transported down the velocity gradient.

Momentum flux is the rate of transport of momentum per unit of area. As we can easily

see, momentum flux has dimension of stress:

[

momentum

]

[

time

]

−1

[

distance

]

−2

[

]

[

]

[

]

−1

[

]

−1

[

]

−2

[

]

[

]

[

]

−2

[

]

−2

[

force

]

[

area

]

−1

. (3.6)

This dimensional result agrees with our physical image in which the process that transports

momentum is friction between layers of different velocity. More precisely, the flux of

momentum in a fluid is the shear stress, τ . Equation (3.4) for momentum transport then

becomes:

τ =−µ

, (3.7)

where µ is called the viscosity (also, dynamic viscosity) of the fluid and the potential

gradient that drives flux of momentum is the velocity gradient taken perpendicularly to the

direction of fluid flow (Fig. 3.2). This is another constitutive relationship for a material.

Just as the thermal conductivity specifies heat flux, viscosity specifies momentum flux or,

in other words, shear stress. For a given velocity gradient, as viscosity increases so does

shear stress and, therefore, the magnitude of the drag force between layers. Momentum is

then homogenized at a faster rate. This agrees with our intuitive concept of viscosity. For

example, if we stir water or motor oil at the same rotational speeds and then stop stirring,

the motor oil will come to rest sooner, because momentum flux = shear stress is higher in

the more viscous oil than in water. Note that mechanical energy is not conserved during

viscous flow, as viscous drag forces engendered by shear stress are dissipative (Chapter 1).

But momentum is a different quantity and it is conserved. In our example, stirring causes

the fluid to heat up by dissipation of mechanical energy. When we stop stirring, momentum

is transported across the fluid via the vessel to the Earth.

In this chapter we will use constitutive relations (3.5) (Fourier’s law) and (3.7) to study

energy transport processes in planetary bodies. The equivalent relation for mass transport

will be discussed in Chapter 12.

3.2 Heat transport by diffusion

3.2.1 Overview of heat transfer processes

Heat diffusion (also called conduction) is a process in which internal energy flows as a result

of the propagation of kinetic energy among microscopic particles (e.g. molecules, atoms,

ions, or electrons), without bulk macroscopic displacement of matter. Internal energy is

127 3.2 Heat transport by diffusion

transported as neighboring particles interact with one another and exchange kinetic energy.

All microscopic kinetic energy modes: translation, rotation and vibration (Section 1.14),

may be involved in the process. Heat advection occurs when there is a net macroscopic

displacement of matter, which exchanges places with other parcels of matter at a different

temperature, so that internal energy is carried by the flow of matter.Although not customary

in the engineering literature, in planetary sciences it is convenient to make a distinction

between advection, as defined above, and convection, which is a process in which heat

is advected as a result of a cyclical motion of matter driven by a temperature gradient

that engenders buoyancy differences. Engineers call this process natural convection, and

distinguish it from forced convection, in which heat advection occurs as a result of motion

of fluid propelled by machineries, such as fans or pumps. As an example of the difference

between advection and convection, consider heat transfer in the Earth’s mantle and heat

transfer by magma ascending along a volcanic feeder conduit. The former is heat advection

resulting from mantle convection, whereas the latter is heat advection without convection

(to an engineer, magma ascent would be an example of forced convection). The processes

of diffusion and advection can only occur within matter. Radiation, in contrast, is a process

in which part of a body’s internal energy is transformed to electromagnetic energy that can

travel through matter only if it is transparent to that specific range of wavelengths, but that

travels unimpeded in the absence of matter. When electromagnetic radiation interacts with

an opaque body it is absorbed and converted to internal energy. Radiation is not an important

heat transfer process in planetary interiors, but it is important in planetary atmospheres and

is the only process by which planetary bodies receive energy from the Sun. We discuss

radiation in Chapter 13.

3.2.2 The diffusion equation

Heat diffusion is part of every heat transfer process. Beyond the obvious case, that it is the

only form of heat transfer that is possible in a rigid body, heat diffusion takes place between

layers of fluid moving at different velocities and at the boundary between a moving fluid

and its rigid environment. Heat diffusion is also responsible for carrying internal energy to

the interior of a rigid body whose surface receives energy by radiation. We seek to construct

an equation that describes heat diffusion in general, allowing for the possibility that both

temperature and temperature gradient vary as a function of space and time. We will also

include the effects of heat sources (e.g. radioactive, gravitational or electromagnetic heat

generation; dissipation of mechanical energy by friction, etc.) and heat sinks (e.g. melting

and metamorphic devolatilization reactions).

We begin by considering an infinitesimal volume element inside a material in which there

is heat flow (Fig. 3.3). We assume that the material is rigid and at rest relative to a coordinate

system fixed to the observer. Our goal is to write the equation for energy conservation in

the infinitesimal volume element. Because the process is assumed to take place at constant

pressure, any net gain or loss of heat corresponds to a change in the enthalpy content of the

volume element, and is reflected in a temperature change given by c

dT , where c

is the

specific heat capacity. The lengths of the sides of the volume element are δx, δy and δz,so

that the heat flow across the element’s left face (amount of heat flowing per unit of time

across a surface with area δy δ z) is given by (see equation (3.5)):

−kδyδz

∂T

∂x



. (3.8)