Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

148 Energy transfer processes in planetary bodies

expressed by equation (3.35) is rigorously true only as long as there are no phase changes

of any of the atmospheric components. For example, we saw in Section 1.12.1 that the

heat associated with phase changes of H

O in the terrestrial atmosphere is not negligible,

rendering dQ = 0 and equation (3.35) invalid in any atmospheric region in which there is

condensation or evaporation of H

O (or any other condensable species, e.g. CO

in Mars or

hydrocarbons in Titan). Finally, we need to choose an equation of state. The atmospheres of

Earth, Mars and Titan are tenuous enough that the ideal gas equation of state is applicable,

but this may not be true for the atmosphere of Venus, nor for the atmospheres of the gas

giants below the top few kilometers (Chapter 9).

For a convective atmospheric layer that can be treated as an ideal gas we have α = 1/T

(Exercise 1.11), so equation (3.35) simplifies to:

. (3.36)

The temperature gradient given by equation (3.36) is a positive quantity called the dry

adiabatic lapse rate. It corresponds to y measured as positive downwards, so that if we

are interested in how temperature changes with elevation we need to take the negative of

equation (3.36). For an ideal gas atmosphere, we can also write the dry lapse rate in terms

of the number rotational and translational of degrees of freedom of the gas molecules, f,as

follows (see equation (2.45)):

2gw

(

f +2

)

, (3.37)

where w is the molecular weight (or proper mass....) of the gas. Clearly, this will work only

if the atmosphere can be considered to be composed of a single gas (e.g. Mars), or if all

the gas species in the atmosphere have the same number of degrees of freedom (Earth).

Calculation of the adiabatic lapse rate in atmospheres in which there are condensable species

is suggested as an end-of-chapter exercise.

3.6 Heat advection

3.6.1 The diffusion–advection equation

To study convection as a heat transfer mechanism we must begin by deriving the equation

that describes heat advection in general. In our derivation of the diffusion equation (equation

(3.15)) we assumed that there was no motion of the material in which heat diffusion takes

place. To describe advection we must specify a reference frame relative to which we measure

the state of motion. A description of the situation to which equation (3.15) applies is that

the material is at rest relative to the observer. If we now allow the material to move relative

to the observer, then there will be heat advection relative to him/her/it as a result of motion

of material in which there is a gradient of internal energy. This is in addition to the heat that

is diffused, and that is described by equation (3.15). We need to add a term to that equation,

called the advective term, to account for the transport of additional internal energy. Let us

assume that the material inside the volume element in Fig. 3.3 is moving relative to an

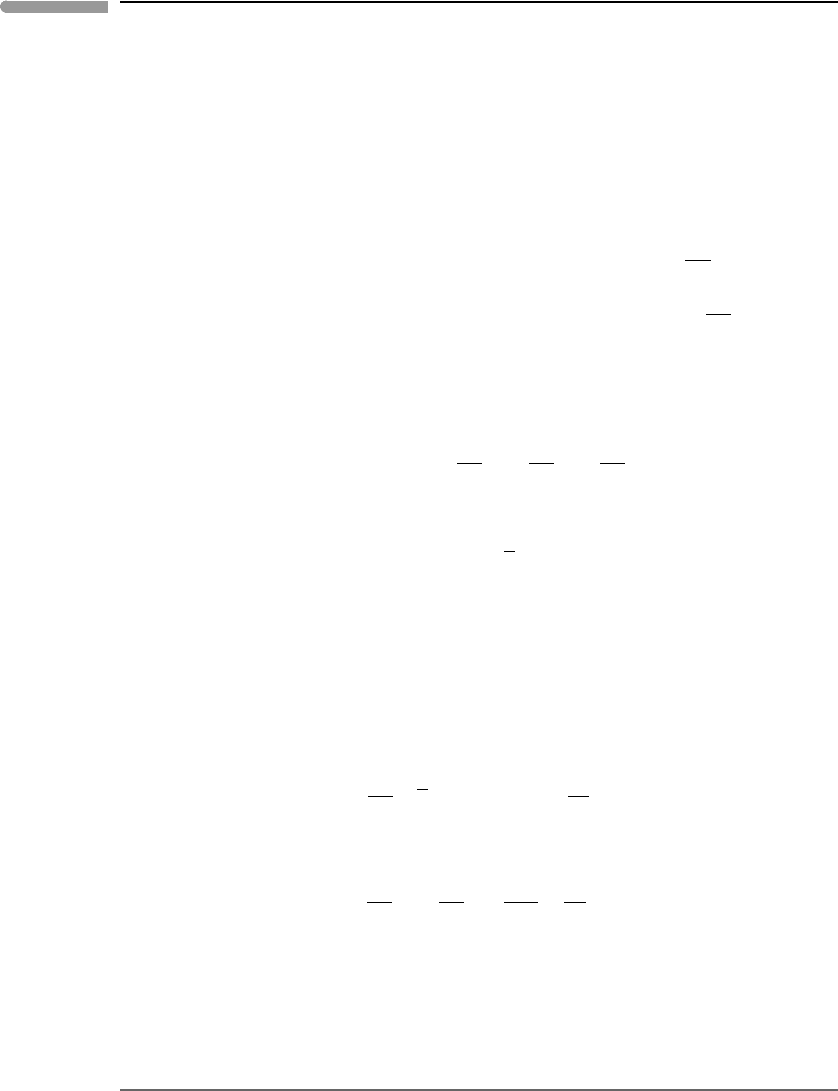
149 3.6 Heat advection

observer with velocity components u

, u

, and u

. The volume element, or equivalently the

coordinate axes, remains fixed relative to the observer, but the material inside the volume

element moves. The volume of material moving in the x direction per unit time is δy δzu

Because the temperatures at x and x+δx are generally different, the net enthalpy advected

per unit time into the volume element in the x direction equals the enthalpy of the incoming

material at temperature T(x) minus the enthalpy of the outgoing material at T(x +δx), as

follows:

δyδzu

ρc

T(x)−δyδzu

ρc

T(x+δx) =−δyδzu

ρc

∂T

∂x

δx

=−δxδyδzρc

∂T

∂x

. (3.38)

Identical arguments applied to the other two orthogonal directions yield the following

expression for the total amount of enthalpy advected into the infinitesimal volume element

per unit time:

−δxδyδzρc



∂T

∂x

∂T

∂y

∂T

∂z



, (3.39)

which can be written more compactly as:

−δxδyδzρc

(u ·∇T

)

, (3.40)

where

u is the velocity vector, with components u

and ∇T is the temperature gradient

(a one-form), with components ∂T/∂x, ∂T/∂y and ∂T/∂z (see also Box 1.1). The total rate of

change in the enthalpy content of the volume element is given by adding equation (3.40)to

equation (3.12).

The rate of change of enthalpy is related to the rate of change in the temperature of the

volume element by equation (3.13). Equating the latter to the sum of (3.12) plus (3.40),

simplifying and rearranging we get:

∂T

∂t

u ·∇T =κ∇

T +

(3.41)

or, in one dimension:

∂T

∂t

∂T

∂x

=κ

∂

∂x

. (3.42)

Equation (3.41) (or (3.42)) is called the diffusion–advection equation, as it accounts for

both modes of heat transfer. It is an energy conservation equation that expresses the First

Law of Thermodynamics. The diffusion equation, (3.14), is a special case of (3.41) with

u =0.

3.6.2 A velocity scale for advection

When material in which temperature is not uniform is in motion, heat transfer occurs by

both advection and diffusion, as described by equations (3.41)or(3.42). An important

question that arises is that of the relative rates at which thermal energy is transported by

advection and by diffusion. Consider a system in a steady state (∂T /∂t = 0) and with no

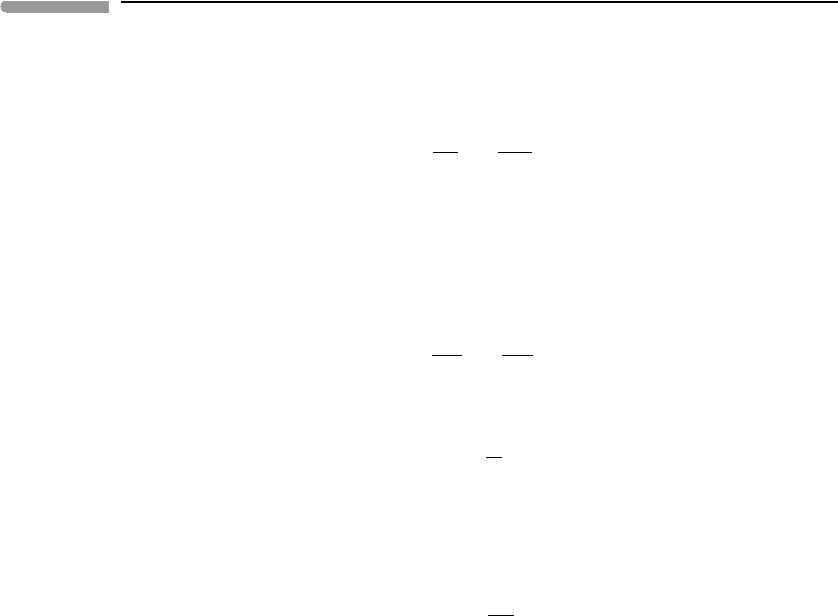
150 Energy transfer processes in planetary bodies

heat generation (α = 0). To simplify notation we drop the subscript x from u

because we

consider heat flow in one dimension. Equation (3.42) becomes:

∂T

∂x

=κ

∂

∂x

. (3.43)

The two sides of this equation represent the advective and diffusive contributions to heat

flow, which in a steady state and with no heat generation must balance one another. Let

M be the characteristic lengthscale of the problem in the x direction, in which material is

moving with velocity u, and such that a finite temperature difference, T, occurs over the

distance M. We then write equation (3.43) as follows:

T

≈κ

T

, (3.44)

which simplifies to:

u ≈

. (3.45)

The ratio κ/M, which has dimensions of [L][T ]

−1

, provides a velocity scale for advective

flow. We can define a non-dimensional velocity by forming the ratio u/(κ/M). This non-

dimensional velocity is called the Péclet number and is symbolized by Pe:

Pe≡

. (3.46)

A value of Pe>1 means that advection outpaces diffusion. The higher the value of Pe,

the less significant diffusive heat transfer is. We could have also arrived at the definition

of Pe by noticing that the product of the characteristic velocity of the problem, u, times its

characteristic length, M, has units of diffusivity, so that the product uM can be thought of

as a measure of the efficiency with which advection diffuses heat. This leads to the same

physical interpretation of the Péclet number.

Measuring the velocity of the advective flow with a non-dimensional number such as Pe

determines the efficiency of advective heat transport independently of the absolute scale

of the problem, just as the non-dimensional parameters ζ and θ describe heat diffusion in

a scale-free way. As an example, consider convection in the Earth’s mantle. If we take a

characteristic rate of plate motion of 10 cm yr

−1

≈3 ×10

−9

−1

as the velocity of mantle

convection, u, and the mantle thickness of ∼3000 km as its characteristic lengthscale M, then

with κ = 10

−6

−1

we get Pe ≈ 9000. This says that the velocity of the advective flow

in the Earth’s mantle is large enough to render heat diffusion negligible, so that the Earth’s

deep interior loses most of its thermal energy by convection. Compare this statement, and

how we arrived at it, with our discussion of diffusive planetary cooling in Section 3.3. The

conclusion that we reached there is the same one that follows from calculating the mantle’s

Péclet number, except that this is a lot simpler and it allows us to make a quantitative

statement. The flaw in Lord Kelvin’s argument about the age of the Earth becomes obvious,

but, of course, calculating the Péclet number requires that we know that the mantle is

convecting in the first place, and the rate at which it convects. Lord Kelvin had no way of

knowing this nor, I believe, did he have any compelling reasons to assume that the mantle

is convecting.

151 3.6 Heat advection

Worked Example 3.2 Heat advection and metamorphic field gradients

Heat transfer within the Earth’s continental crust is primarily by diffusion. There are some

obvious exceptions to this statement, such as regions of active magmatic emplacement and

regions of permeable fluid flow. In the absence of local perturbations such as these, one

could expect that the geothermal gradient in the continental crust can be approximated as a

steady-state conductive temperature distribution (see Turcotte & Schubert, 2002, Chapter 4

for an in-depth discussion of continental geotherms). But is this always the case? Consider

denudation of metamorphic rocks equilibrated at depth, or burial of surface rocks. Rocks

will stay on the steady-state diffusive geotherm only if they are uplifted or buried with

a Péclet number of order 1 or less. If Pe ! 1 then their temperature will not be able to

adjust fast enough to what the steady-state geotherm would be, and a transient temperature

distribution, either hotter or colder than the steady-state geotherm, will develop (Fig. 3.10).

In order to estimate the maximum rate of burial or denudation that can preserve the

conductive geotherm we set the non-dimensional velocity Pe = 1 and solve equation 3.46

for u. We take the characteristic length of the problem, M, as being of the order of the

thickness of the continental crust, ∼30 km. With κ =10

−6

−1

, we obtain u ∼3 ×10

−11

−1

∼1mmyr

−1

. This rate is comparable to the rate of denudation of active mountain

100 200 300 400 500 60

Depth (km)

Temperature (

Steady state

diffusive geotherm

Burial with Pe >> 1

Blueschist

Denudation with Pe >> 1

Buchan

Denudation with

Barrovian

Fig. 3.10 Schematic view of three metamorphic ﬁeld gradients. If metamorphic rocks are unroofed with a Péclet number ∼1

their temperature will approximately follow the steady state diffusive geotherm. The resulting assemblages

correspond to those of Barrovian metamorphism. High-temperature/low-pressure Buchan assemblages can form if

denudation occurs with Pe !1. Low-temperature/high-pressure blueschist metamorphism requires burial with

Pe !1.

152 Energy transfer processes in planetary bodies

belts, but is one to two orders of magnitude slower than characteristic rates of tectonic

processes. If we take the latter rates to be in the range 1–10 cm yr

−1

, then an average

estimate for u in tectonically active areas is

√

(10 ×1) cm yr

−1

≈10

−9

−1

, leading to Pe

≈30. In areas of active tectonic activity, therefore, diffusive heat transfer is modest relative

to advection and the geothermal gradient cannot correspond to a steady-state diffusive

temperature distribution. It is important to understand that advection in this case has nothing

to do with motion of fluids of any kind and occurs entirely as a result of motion of solid

rock by some combination of faulting, ductile shearing and folding.

These contrasting modes of heat transfer are expressed in the metamorphic field gradients

of exposed orogens, which are the thermal gradients preserved in metamorphic assemblages

exposed at the surface but equilibrated over a range of pressures (see, for example, the clas-

sic text by Miyashiro, 1994). Metamorphic field gradients tend to cluster in three distinct

regions of P -T space which, in order of increasing temperature at a fixed pressure, are

often labeled Blueschist, Barrovian and Buchan. Metamorphic field gradients are not fossil

geotherms, because rocks at different depths do not attain their metamorphic peak temper-

atures simultaneously, but it can be shown that Barrovian metamorphism develops when

rocks are able to stay close to a diffusive geotherm during uplift and denudation (see Patino

Douce et al., 1990). This is only likely to happen if the core of an orogenic belt is denuded by

erosion. The other two metamorphic field gradients must therefore develop in environments

in which advection is the dominant mode of heat transfer, and in which the crust is either

heated (Buchan) or cooled (Blueschist) relative to the steady-state diffusive geotherm, in

response to tectonic activity. Blueschist metamorphism requires fast tectonic burial of cold

material (Fig. 3.10), which characteristically takes place at subduction zones and during the

initial stages of continental collisions. Buchan metamorphic conditions may develop during

tectonic collapse of orogenic belts, where low-angle detachment faulting leads to tectonic

unroofing of deep-seated rocks with Pe ! 1.

In this analysis we ignored the geometry of the environments in which metamorphism

takes place, but as we shall see in the following paragraph this can be an important consid-

eration. For instance, there is a minimum thickness that a fault block must have in order to

be able to preserve its internal temperature unperturbed during tectonic displacement.

Consider the geometry sketched in Fig. 3.11. Advective flow occurs in the x direction

only and heat transport perpendicular to this direction is by diffusion (u

=0). We ask what

is the distance, λ, that a thermal perturbation will propagate by diffusion perpendicular to

the direction of advective flow. This length scale is related to the diffusion time scale

by equation (3.16): λ ∼ 2

√

κτ. Because we want to compare advective and diffusive

lengthscales, we make τ equal to the time that the advective flow takes to cover the

characteristic advective lengthscale, M, i.e. τ = M/u

. From this identity and the definition

of Pe:

Pe=

κτ

(3.47)

or:

M =

√

κτ ∼

√

Pe, (3.48)

153 3.7 Convection as a heat transport mechanism

Pe = (u

Λ)/κ

Fig. 3.11

A rigid slab of thickness λ moves with velocity u

in the x direction, in which temperature changes occur over a

characteristic length M. Heat transfer in the y direction is by diffusion. The geometry is a reasonable model for the

oceanic lithosphere.

which yields the following scaling relationship, valid only for the geometry sketched in

Fig. 3.11:

∼2Pe

−1/2

. (3.49)

The geometry of sea-floor spreading corresponds to that of Fig. 3.11 The mantle flows

horizontally away from mid-ocean ridges and as it cools it gives rise to the rigid lithosphere,

in which vertical heat transfer is by diffusion.The thermal perturbation that we are interested

in is the exposure of hot asthenospheric mantle to the temperature at the surface of the

Earth. What we are asking is what is the thickness of mantle (± crust) that will cool down

significantly while it is being transported laterally by mantle convection. In other words,

what is the thickness of the oceanic lithosphere?As we saw previously, for the Earth’s mantle

Pe ≈ 9000, so that with M = 5000 km (= characteristic width of an oceanic plate) we get

λ ∼105 km, which agrees reasonably well with the thickness of the oceanic lithosphere.

3.7 Convection as a heat transport mechanism

We have discussed the energetic underpinnings of convection (Section 3.4) and we have

derived a general expression for the adiabat in a convective fluid (Section 3.5). We have

also found a general equation that describes advective heat transport (Section 3.6). Our

next task is to derive the mathematical equations that describe heat transport by convection.

This is not simple. A complete mathematical description of convection in a system such

as a planetary mantle, core, atmosphere or magma chamber seeks to describe the precise

geometry of the convective flow and its evolution with time. Exact analytical solutions

generally do not exist, and the significance of numerical solutions is sometimes hard to

assess, owing in part to the fact that solutions tend to be quite sensitive to the choice of initial

and boundary conditions, and also because there are significant uncertainties in material

properties, chemical composition and phase transformations. Our goal is more modest. We

seek to lay out the basic principles of what is called parametrization of convection, which

consists of developing a set of relatively simple equations that yield order of magnitude

estimates for global parameters such as heat flux and convective velocity, while ignoring

the local geometry and temporal evolution of the convective flow. It is a remarkable fact

that all of these equations are functions of a single parameter that encapsulates the dynamics

of convection, i.e. the forces that drive and oppose convective flow.

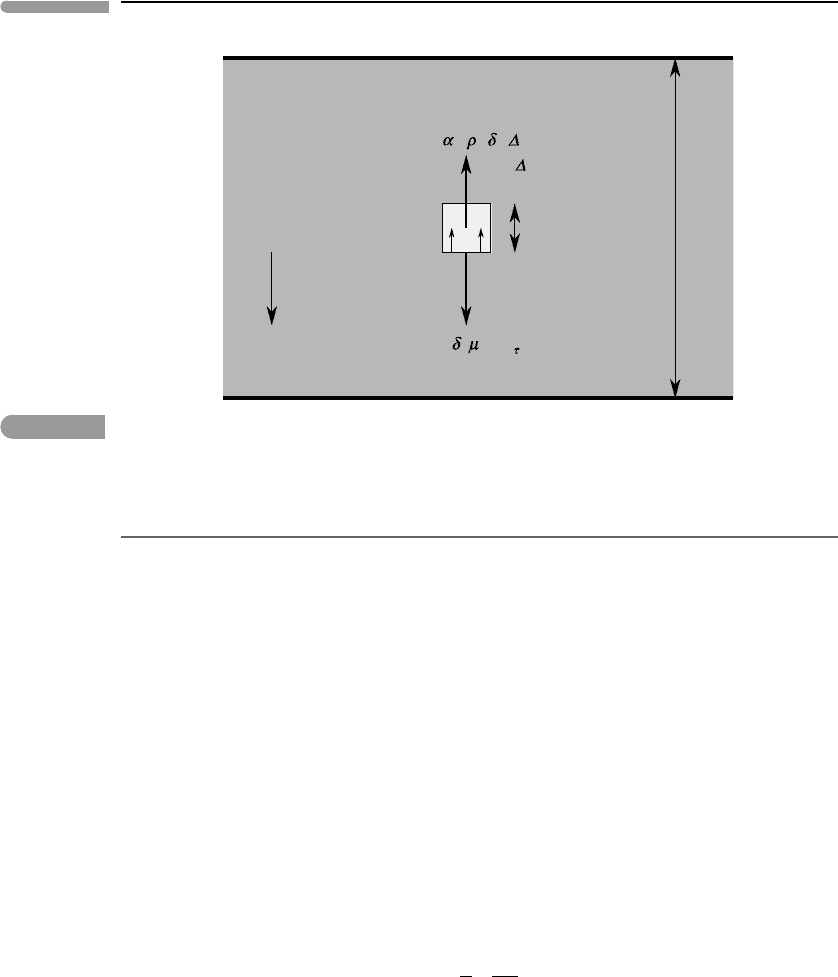
154 Energy transfer processes in planetary bodies

B~- g

F~-(

( T>0)

Fig. 3.12

The forces acting on an element of ﬂuid of characteristic linear dimension δ, inside a ﬂuid layer of thickness D, are

buoyancy, B, and viscous drag, F. The sign convention is positive upwards, so that gravity, g, is negative.

3.7.1 Dynamics of thermal convection

We wish to derive a criterion that will allow us to decide whether convection will take place

in a fluid layer. Consider a fluid layer of depth D, and in it a fluid element of characteristic

linear dimension δ, see Fig. 3.12. Convection will take place only if the fluid element is

buoyant throughout the thickness of the layer. The buoyancy, B, is a gravitational force that

acts on the fluid element and that arises from the difference, ρ, between its density and

that of the surrounding fluid. The volume of the fluid element is of order δ

, so:

B ∼ gδ

ρ . (3.50)

Because g, which is directed towards the center of the planet, is negative (equation (1.7)) a

mass deficit (ρ < 0) results in a positive buoyancy force, i.e. directed upwards, as expected.

In the case of thermal convection the density contrast is a consequence of a difference in

temperature, but convection can also be driven by compositional gradients or, in the case of

double-diffusive convection, by both temperature and composition gradients. Staying for

now with thermal convection, we use the definition of the coefficient of thermal expansion,

α (equation (1.66)), to find the effect of temperature on density at constant pressure:

α =−



dρ



, (3.51)

Integrating this equation between a reference state T

, ρ

and any arbitrary state T, ρ we

get:

ρ =−ρ

−α

(

T −T

)

. (3.52)

A useful approximation is that, for small x,ln(1 −x) ≈−x, or, equivalently, e

−x

≈ 1 −x.

The coefficient of thermal expansion for solids and liquids is small (typically of order 10

−5

−1

, see also Chapter 8), so that, for all reasonable temperature contrasts (of order 10

K),

155 3.7 Convection as a heat transport mechanism

this approximation is valid. The density contrast is then given by:

ρ = ρ −ρ

≈−αρ

(

T −T

)

≈−αρ

T , (3.53)

where T is the temperature contrast that drives convection. This corresponds to the tem-

perature change that takes place at the heat transfer boundaries of the convection cycle, for

example T

−T

or T

−T

in Fig. 3.9. The temperature change along the adiabatic paths

−T

or T

−T

) does not generate buoyancy differences, because it affects equally all

fluid elements in the layer. Convection can take place only if there is a temperature differ-

ence between the boundaries once the effect of the adiabatic gradient has been subtracted.

This condition is described by saying that the temperature difference across the convecting

fluid layer is superadiabatic. It is equivalent to our statement in Section 3.4 that convection

is only possible if there are at least two heat transfer boundaries that separate the upwelling

and downwelling adiabats.

As the fluid element ascends it cools by diffusing heat to its surroundings. Buoyancy will

be maintained only as long as a significant temperature contrast exists. We can reasonably

postulate that convection will only take place if the time that the fluid element takes to rise

through the thickness of the fluid layer, which we can call the convection time t

, is small

compared to the characteristic diffusive cooling time of the fluid element, t

. The latter is

given by equation (3.16):

∼

4κ

(3.54)

and t

by:

∼

, (3.55)

where u is the characteristic velocity that describes vertical motion of the fluid.

Buoyancy, equation (3.50), is opposed by a frictional force that arises from viscous drag.

In all of the examples that we will consider in this book it is acceptable to neglect changes

in momentum of the fluid, i.e. we will only consider cases in which fluids move with

constant velocity. If this is the case then viscous drag must exactly balance buoyancy, so

that there is no net force acting on the fluid element. The frictional force, F, is the product

of the shear stress acting on the surface of the fluid element times the surface area of the

fluid element. The shear stress is given by equation (3.7). If velocity decays from its value

u at the boundary of the fluid element to zero over a characteristic length δ

, then we

can write:

τ =−µ

≈−µ

. (3.56)

The surface area of the fluid element is of order δ

, so that the viscous drag (=total frictional

force) is:

F ∼−δ

τ ∼−

µu

. (3.57)

156 Energy transfer processes in planetary bodies

This force equals the buoyancy force, equation (3.50), see also Fig. 3.12. Therefore, using

(3.53):

−

µu

∼gδ

ρ =−gδ

αρ

T . (3.58)

Solving for u and substituting in (3.55):

∼−

µD

gρδδ

µD

gαρ

T δδ

. (3.59)

Recall that we are interested in the ratio t

, which includes the factor δ

. The problem

with these equations is that they contain three different lengthscales: D, δ and δ

. Of these,

only the first one is well defined, as it is the thickness of the fluid layer. In order to define

the values of δ and δ

it is necessary to specify the geometry of the problem, so that it is

not possible to specify general values for these two lengthscales. The only way to come up

with a result of general validity is to define the timescales for diffusion and convection in

terms of the only lengthscale of the problem, which is the thickness of the fluid layer, D.

The diffusive and convective time scales defined in this way become:

d,D

≡

4κ

(3.60)

and:

c,D

≡

µD

gαρ

T D

gαρ

T D

. (3.61)

The ratio between these two time scales, omitting numerical factors, is the definition of a

non-dimensional parameter known as the Rayleigh number, and symbolized by Ra:

Ra ≡

d,D

c,D

gαρ

T D

µκ

. (3.62)

The Rayleigh number gives an indication of the tendency of the fluid layer to convect.

The greater the value of Ra, the longer the diffusion timescale is relative to the convection

timescale, and therefore the more likely it is that the fluid layer will undergo convective

overturn, because parcels of fluid will be able to traverse the thickness of the layer without

cooling down significantly. There is a critical value of the Rayleigh number, Ra

, that

marks the onset of convection and hence the transition between diffusive and convective

heat transport. The actual critical value depends on the geometry and boundary conditions

of the problem, so that there is no universal value of Ra

. This is to be expected, because in

equations (3.60) and (3.61) we substituted the fixed lengthscale D for the two lengthscales

that depend on the particular configuration of the fluid layer, δ and δ

. Exact analytical

solutions for Ra

are available for some simple cases; in many other instances its value can

only be determined numerically or experimentally.

For a laterally extended layer (in which the width is much greater than D) heated from

below, which is a reasonable approximation to planetary mantles and tabular igneous intru-

sions, Ra

is of order 10

–10

. Typical values for the parameters in equation (3.62) for

the Earth’s mantle are: D = 3000 km; α = 10

−5

−1

; ρ

= 3500 kg m

−3

; µ = 10

s; κ = 10

−6

−1

; g = 9.8ms

−2

; T = 1400 K. The value of T is the temperature

157 3.7 Convection as a heat transport mechanism

difference across the oceanic lithosphere, which is the temperature drop that corresponds

to the low-pressure cooling leg of the convection cycle (CD in Figs. 3.8 and 3.9). This is

the temperature difference that engenders negative buoyancy at the top of the mantle and

thus drives convection. With these numbers we find that Ra for the Earth’s mantle is ∼10

This value is so much higher than the critical value that one must conclude that the Earth’s

mantle is not only convecting, but doing so vigorously. This is also reflected in its high

Péclet number (Section 3.6.2). Note an important conceptual difference between Ra and

Pe, however. The Rayleigh number is based on the dynamics of fluid flow and is an a priori

predictor of whether or not a fluid layer is likely to convect. Calculation of Pe starts from

the knowledge that advective heat transfer is taking place and its value is a measure of the

efficiency of advection as a heat transfer mechanism.

3.7.2 The thermal boundary layer

In Section 3.6.2 we calculated the thickness of the oceanic lithosphere by specifying that

heat flow across it takes place solely by diffusion. In the terminology of heat transfer, the

lithosphere is the thermal boundary layer of mantle convection. When diffusion is the only

heat transfer mechanism the thermal boundary layer is the thickness of material across

which most of the thermal gradient occurs (Section 3.2.4, Fig. 3.5). This is also true of

advection but in this case the reason why most of the temperature gradient occurs across

the thermal boundary layer is that heat transfer across it is by diffusion, whereas motion of

matter transports internal energy throughout the remainder of the system, where advection

outpaces diffusion (see Section 3.5).

The thermal boundary layer is the main barrier to heat transfer, because diffusion is a

much less efficient heat transfer mechanism than advection. As heat transfer across the

boundaries is what drives convection (Section 3.4), it follows that the nature and thickness

of the thermal boundary layer is what ultimately controls the nature of convection. Figure

3.13a is a schematic view of the thermal boundary layer. Let x be the direction parallel to

the thermal boundary layer, and hence to the heat transfer interface, and y be perpendicular

to it. Fluid velocity in the y direction, u

, vanishes in the thermal boundary layer but has a

non-zero, and perhaps variable, value in the remainder of the fluid layer. The velocity in the

x direction, u

, varies between some characteristic value inside the actively convecting layer

and zero at the boundary. The top diagram in Fig. 3.13 shows a continuously decreasing

velocity profile, but this is not always the case, as we shall see. The key point is that there is

no heat advection in the y direction across the thermal boundary layer, because u

vanishes

in it. We can think of the thermal boundary layer as being made up of a number of layers

moving parallel to one another, like the cards in a deck. Regardless of the actual distribution

of velocities throughout the thermal boundary layer, heat transfer between adjacent layers,

and hence across the entire thermal boundary layer, can take place only by diffusion. If the

system has been convecting long enough to have reached a steady state, and there is no heat

generation in the thermal boundary layer, then the temperature gradient across the thermal

boundary layer is linear, from T

at the heat transfer interface to the temperature of the

actively convecting fluid, T

. This is not the case in the convective interior, where heat is

advected in the y direction, with u

∼u

. We will consider the temperature in the convecting

fluid to be constant, as shown in Fig. 3.13a. An adiabatic gradient can be superimposed on

this temperature distribution but this has no effect on the arguments that follow.