Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

158 Energy transfer processes in planetary bodies

Thermal

boundary

layer

Thermal boundary layer

Rheological boundary layer

No slip boundary

Moving plates

Stagnant lid

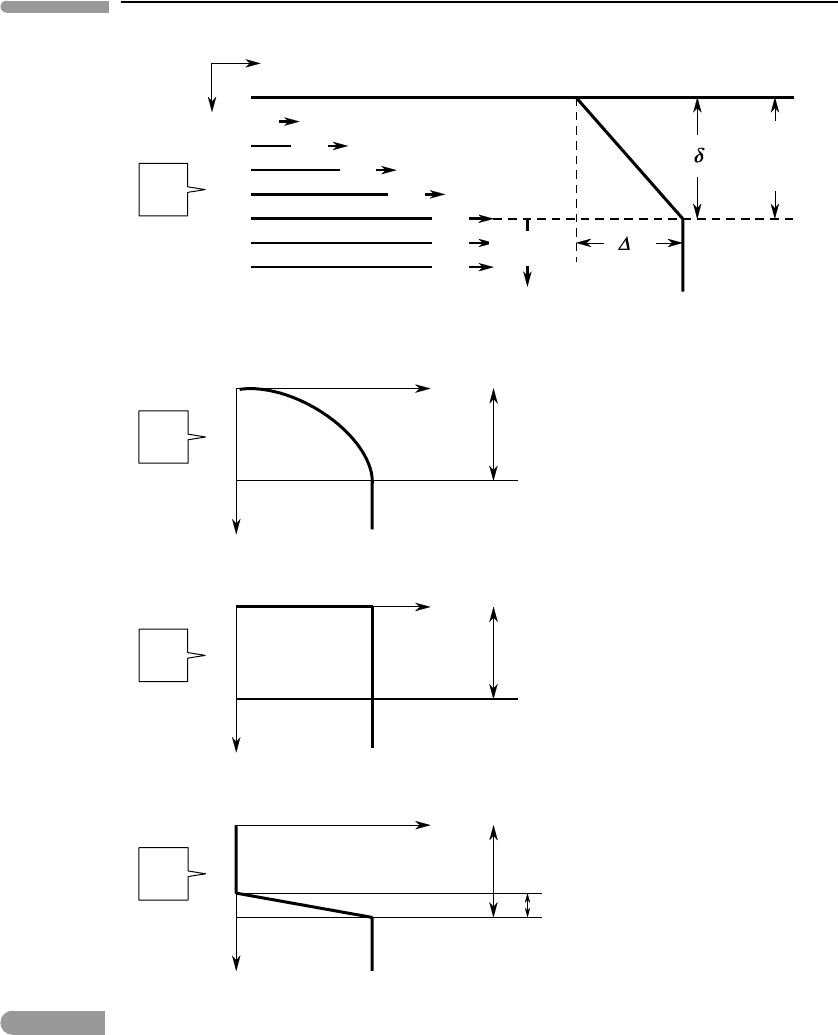
Fig. 3.13

Convective thermal boundary layer. A generalized thermal boundary layer in x–y space is shown in (a). The velocity

distribution inside the thermal boundary layer is shown with the arrows of variable length, and the temperature

distribution with the thick line. Different types of boundary layers are shown in (b) through (d) in terms of the

magnitude of the velocity in the x direction, u

, as a function of y.

159 3.7 Convection as a heat transport mechanism

The effectiveness of convection as a heat transport mechanism is controlled to a large

extent by the velocity distribution across the thermal boundary layer. This is in turn deter-

mined by a number of factors, including material properties, temperature and temperature

gradient, and convective velocity. For example, if velocities are high enough that frictional

forces at the boundary are non-negligible then the velocity must vanish at the interface.

This is called a no slip boundary. The velocity in the boundary layer then varies continu-

ously (but not necessarily linearly) from 0 at the interface to the velocity of the actively

convecting fluid (Fig. 3.13b). This is the case, for example, at the interface between ocean

and atmosphere. Plate tectonics is different, as in this case friction at the interface (i.e. the

ocean floor) vanishes owing to the very small velocity. In this case u

is constant across the

thermal boundary layer (the oceanic lithosphere) and equal to the velocity in the actively

convecting mantle, and there is a velocity discontinuity at the interface (Fig. 3.13c). The

thermal boundary layer forms because the mantle close to the surface cools to the point

where it cannot flow anymore, forming a rigid lid on the ductile asthenosphere. What is

special about plate tectonics is that the lid is broken into plates that are able to subduct,

allowing fragments of diffusive lid to be carried along by mantle convection.

Formation of the rigid lid takes place because there is a strong inverse relationship

between temperature and viscosity (Box 3.3). In the case of plate tectonics, however, the

Box 3.3

Temperature effect on viscosity

For many materials, including mantle rocks, it is found that viscosity varies with temperature following an

inverse exponential law that is called Arrhenius’s law (see Chapter 12). A dependency on strain rate (called

non-Newtonian rheology) may be superimposed on Arrhenian behavior, but that is beyond the scope of this

book. The Arrhenius law for viscosity can be written as follows:

µ = Ke

, (3.3.1)

where K and E

are material properties and R is the gas constant. If we restrict temperature to a relatively

narrow interval we can deﬁne an (arbitrary) reference temperature T

within this interval and, given the

viscosity µ

at this temperature, we can calculate the viscosity at any other temperature inside the interval

by:

µ = µ

−T

, (3.3.2)

which, if T and T

are not too different, we can approximate as follows:

µ ≈ µ

−γ

(

T−T

)

(3.3.3)

with the parameter γ deﬁned as follows:

γ =

. (3.3.4)

Equation (3.3.3)isalinearized approximation to Arrhenius’s law. The material property E

is called the

activation energy for viscous ﬂow (see Chapter 2). Typical values for mantle materials are µ

≈10

Pasat

= 1950 K, and E

≈300 kJ mol

−1

160 Energy transfer processes in planetary bodies

contrast in viscosity between lithosphere and asthenosphere, which spans many orders of

magnitude, is masked by the fact that the lithosphere can break and thus move. Consider

now the cases of Mars or Venus. A case can be made for both planets that convection

takes place below the rigid outer layer (Section 3.8.2), but there is no evidence that this

outermost layer is broken up and carried along by the underlying convective flow. For

example, there are no subduction zones nor transform faults on either of the planets and

volcanoes are not arranged in Hawaii-style volcanic chains. Venus and Mars are examples

of what is called stagnant lid convection, depicted in Fig. 3.13d. The strong inverse effect

of temperature on viscosity generates a rigid lid, but in this case the lid does not break up.

The velocity gradient is then concentrated in a relatively thin layer called the rheological

boundary layer, sandwiched between the stagnant lid and the actively convecting fluid. The

y velocity component does vanish in the rheological boundary layer, so that it is part of the

thermal boundary layer (see Fig. 3.13d).

The driving force for thermal convection derives from buoyancy engendered by tem-

perature differences which in turn are caused by heat transfer across the thermal boundary

layer (Section 3.4). Some part of the thermal boundary layer must always be entrained

in the convective flow. It is in this part of the thermal boundary layer that buoyancy is

generated. In the case of convection with moving plates (Fig. 3.13c) the entire thermal

boundary layer enters the convective flow (e.g., at a subduction zone), so that the full tem-

perature difference T (Fig. 3.13a) is available to drive convection. In contrast, convection

with a stagnant lid is driven only by that fraction of T that occurs across the rheological

boundary layer, which is the only part of the thermal boundary layer that is entrained in

the convective flow and that generates buoyancy. We can expect that, other things being

equal, convection with a stagnant lid is less efficient at transporting heat than moving plate

convection.

3.7.3 Scaling of heat transport by convection

Consider a convective layer of thickness D capped by a thermal boundary layer of thickness

δ, where in general it is δ  D. If the system is in a steady state then the heat flux across

the convecting fluid layer, q, must equal the heat flux across the thermal boundary layer.

By Fourier’s law, and with the convention that heat flux q is always a positive quantity

(Section 3.2.4) we have:

q = k

T

, (3.63)

where T is the temperature difference across the thermal boundary layer. We now compare

this to the heat flux that would exist across the entire fluid layer if it was not convecting,

i.e. if heat diffused across the entire thickness D driven by the same temperature difference

T. We label this heat flux q

∗

T

. (3.64)

The advective heat flux, q, and the hypothetical diffusive flux, q

∗

, are driven by the

same temperature difference. The ratio between q and q

∗

is therefore a measure of how

much more efficiently advection transports heat relative to diffusion. This ratio defines a

161 3.7 Convection as a heat transport mechanism

non-dimensional parameter called the Nusselt number, Nu:

Nu≡

∗

T

. (3.65)

The Nusselt number is the non-dimensional advective heat flux, just as Pe is the non-

dimensional advective velocity. Nu is also the ratio between the thickness of the fluid layer

and the thickness of the thermal boundary layer.

Worked Example 3.3 Heat transfer efficiency of terrestrial mantle convection

In the case of convection with moving plates, such as Earth’s plate tectonics, the entire ther-

mal boundary layer moves with the same velocity as that of the convecting fluid (Fig. 3.13c).

If the thickness of the fluid layer, D, is comparable to its characteristic lateral dimension

then D and the thickness of the thermal boundary layer, δ, scale according to equation (3.49),

i.e.:

∼2Pe

−1/2

. (3.66)

We can then derive the following scaling relationship between Nu and Pe:

Nu∼

1/2

. (3.67)

Note that (3.67) applies only to convection with moving plates, as we have explicitly used

the geometry of this type of thermal boundary layer in the derivation of this equation. Since

Pe and Nu are both non-dimensional numbers, there is no mathematical requirement that

they be related by any specific type of function. This is true of any scaling relationship

among non-dimensional numbers.

For the Earth’s mantle, with Pe ≈9000 (Section 3.6.2), weget Nu ∼50. Mantle convection

cools the Earth 50 times faster than diffusion would. It may sound counterintuitive, but this

is the explanation for why Kelvin’s age estimate was too low. In a diffusive Earth most of

the planet would not have began cooling after 4.5 billion years (Fig. 3.6). In contrast, in a

convective Earth the deep interior of the planet contributes to surface heat flow from the

very inception of the convective regime, most likely immediately after differentiation. A

convective planet will cool down completely and meet its thermal demise much faster than

if the same planet cooled by diffusion. It is ironic, in view of his argument with geologists,

that Kelvin’s diffusive model implied that the Earth would have had a much longer life

expectancy than what our rapidly cooling planet actually has (disregarding, of course, the

fact that the Sun will burn out before diffusive cooling could have had time to reach the

center of the Earth).

We can also use equation (3.67) to estimate the rate of mantle convection in the Earth.

Let the average mantle heat flux be q

and assume that heat production in the oceanic

lithosphere is negligible. We write equation (3.65) as follows:

Nu=

kT

. (3.68)

162 Energy transfer processes in planetary bodies

From equations (3.46) and (3.67), making M = D, we have:

Nu∼

1/2





1/2

. (3.69)

We can eliminate Nu between these two equations and solve for u, the velocity of the mantle

flow:

u ∼4

Dκ

(

T

)

. (3.70)

The value of q

in this equation is the average oceanic heat flux of 100 mW m

−2

(Box 3.2).

Other characteristic mantle values are: D = 3000 km, T = 1400 K, κ = 10

−6

−1

and

k = 3Wm

−1

. We then estimate u ∼ 6.8 ×10

−9

−1

≈ 20 cm yr

−1

. This is a factor

of 3 higher than typical rates of plate motion. Agreement is not great, but it is within an

order of magnitude.

3.7.4 Energy conservation in a convecting fluid

The goal of the parametrized description of convection is to generate estimates for heat flux,

convective velocity and thickness of the thermal boundary layer in terms of the Rayleigh

number, depth of the convective layer, temperature change at the heat exchange boundaries

(e.g. Fig. 3.8), and nature of the thermal boundary layer (i.e. stagnant or moving). If we

need to solve for three unknowns: heat flux, q, convective velocity, u and thickness of

the boundary layer, δ, we need three independent equations relating these variables. We

already have two of these equations: (3.63), which gives the relationship between heat

flux and thickness of the thermal boundary layer, and (3.66), which relates thickness of

the thermal boundary layer to fluid velocity. The third equation must be one that relates

heat flux to velocity. Recall from equation (3.7) that the velocity gradient determines shear

stress in the fluid, and that shear stress in turn determines the rate of heating by viscous

dissipation (Chapter 1). This suggests that fluid velocity and heat flux must be related by an

energy conservation equation, which in a convecting fluid must be the diffusion advection

equation. We write equation (3.41) in two dimensions:

∂T

∂t

∂T

∂x

∂T

∂y

=κ



∂

∂x

∂

∂y



(3.71)

(do not confuse α in this equation, which is the rate of heat production per unit mass, with the

coefficient of thermal expansion). Consider a fluid layer of depth D in the y direction, capped

by a boundary layer of thickness δ (Fig. 3.14). We are interested in steady state conditions

with no horizontal thermal gradient, so ∂T/∂t and ∂T/∂x vanish. We will now substitute a

fictional but mathematically equivalent picture for heat transfer inside the convecting fluid.

Imagine that the vertical velocity component, u

, vanishes everywhere in the convective

fluid, and that the advective heat flux in the y direction is accounted for by diffusion with a

large but fictive value of the thermal conductivity, k

∗

. It will not be necessary to calculate

the value of k

∗

, all that we need to keep clear is that it is the thermal conductivity that

the fluid would have to have in order to transport heat in a steady state at the same rate

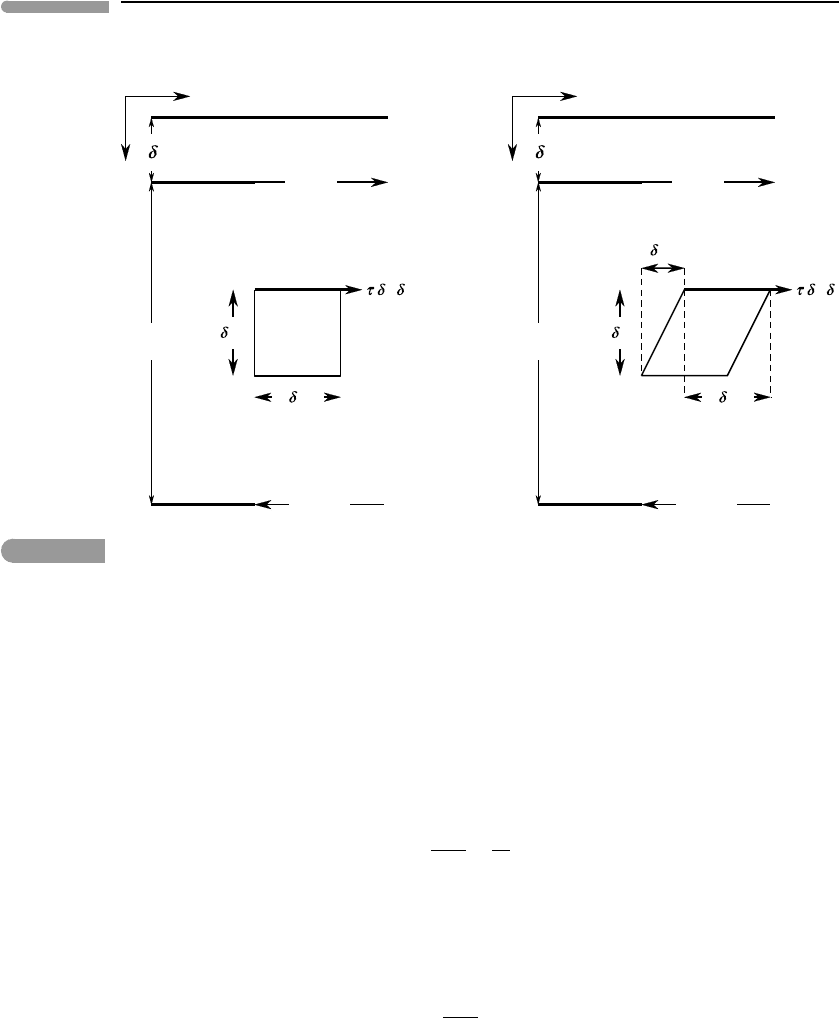
163 3.7 Convection as a heat transport mechanism

-u

time = 0 time = 1

x z x

Fig. 3.14

Viscous dissipation in an element of convecting ﬂuid. The dimensions of the ﬂuid element are δx, δy and δz (coming

out of the page). The force acting on the horizontal faces of the element is τ δxδz. The horizontal velocity changes by

an amount δu

over length δy, so that the top surface of the element moves a distance δu

in unit time. Horizontal

velocity varies from u

to –u

over the thickness D of the ﬂuid layer. The thermal boundary layer has thickness δ.

as convection, assuming that the temperature gradient is the same adiabatic temperature

gradient present in the convective layer. In contrast to the vertical velocity, we will make no

assumptions about the horizontal velocity, u

, which does not vanish. With these constraints

we can drop the partial derivative symbols because ∂T/∂t =∂T/∂x=∂

T/∂x

= 0, and

equation (3.71) simplifies to:

∗

=0, (3.72)

where κ

∗

is the heat diffusivity that corresponds to the fictive conductivity k

∗

. From the

definition of heat diffusivity, κ =k/(ρ c

), and following the convention that heat flux is

always a positive quantity, this equation can be re-written as follows:

−k

∗

+φ = 0, (3.73)

where φ = αρ is heat production per unit volume. If we consider a simple case in which

there are no phase changes nor radioactive heat generation in the fluid layer, and in which

the fluid is a perfect electrical insulator, then the only source of heat is viscous dissipation

of mechanical work.

Consider an infinitesimal volume of fluid with dimensions δx, δy, δz (Fig. 3.14, in which

δz comes out of the page). The viscous stress is given by equation (3.7), which, if horizontal

164 Energy transfer processes in planetary bodies

velocity changes with depth, we write as follows:

τ =−µ

≈−µ

δu

δy

, (3.74)

where δu

is the difference in velocity between the top and bottom of the infinitesimal fluid

volume. The viscous force that acts on the horizontal surface of this volume (perpendicular

to the page) is:

τ δxδz ≈−µ

δu

δy

δxδz. (3.75)

In unit time this force moves a distance δu

, as this is how much the top horizontal face

is displaced relative to the bottom one (see Fig. 3.14). The total rate of dissipation of

mechanical energy is τ δxδzδu

, and the rate of energy dissipation per unit volume is:

τδxδzδu

δxδyδz

≈−µ



δu

δy



. (3.76)

This is work performed by the viscous force on the system, where “the system” is the

infinitesimal volume element. The result of equation (3.76) is always a negative quantity.

In the language of the First Law and with our sign convention (dW > 0 is work performed

by the system), this means that “the environment” always performs work on “the system”.

The system, i.e. our infinitesimal volume element, absorbs this energy as heat. The rate of

viscous heating per unit volume is thus the negative of equation (3.76), i.e.:

φ ≈µ



δu

δy



. (3.77)

Taking the small increments to the limit we rewrite equation (3.73) as follows:

−k

∗

+µ





=0. (3.78)

We now approximate the values of the derivatives by averaging over the depth of the fluid

layer, D.Ifu

is the characteristic fluid velocity, then the horizontal velocity must change

from u

to −u

over the distance D (Fig. 3.14), hence we can write:





≈





. (3.79)

Also, from:





(3.80)

we see that we can approximate this term starting from the thermal gradient across the fluid

layer. Because the fluid is convecting the thermal gradient is adiabatic, so we can substitute

equation (3.35), as follows:

∗





∗



αgT



αg



∗



. (3.81)

165 3.8 Parametrization of convection in planetary interiors

Since we are averaging the derivatives over the depth of the fluid layer the expression in

parentheses in the last term in equation (3.81) is the heat flux across the convective layer, q,

which is also the heat flux across the thermal boundary layer. Hence (with the convention

of q always positive):

∗

≈

αg

q. (3.82)

Substituting equations (3.79) and (3.82) into (3.78) we arrive at the following equation for

energy conservation averaged over the thickness of the fluid layer, which relates heat flux

to velocity:

αg

q ≈ 4µ





. (3.83)

Note that α in this equation is the coefficient of thermal expansion.

3.8 Parametrization of convection in planetary interiors

The interiors of many planetary bodies in the Solar System, present and past, can be dis-

cussed on the basis of either moving plate or stagnant lid convection. The goal of this section

is to develop simple mathematical descriptions of these two convection modes, that capture

some of the essential physics of the processes without getting into any of the details. A

very complete and rigorous discussion of mantle convection, including the gory details, is

presented in the massive treatise by Schubert et al. (2001). It is my hope that the material

that I present here will serve as an introduction to that work for the motivated reader.

3.8.1 Convection with moving plates

The parametrized solution for convection with moving plates is a set of values {q, u, δ}

that simultaneously satisfy equations (3.63), (3.66) and (3.83). We rewrite the equations

in terms of a single characteristic velocity, u, make M = D, and convert Pe to dimensional

velocity using (3.46). The three equations become, respectively:

q = k

T

(3.84)

δ ∼ 2



κD



1/2

(3.85)

αg

q ≈ 4µ





. (3.86)

Combining (3.84) and (3.85) to eliminate δ:

q ∼

kT



κD



1/2

(3.87)

and eliminating u between (3.86) and (3.87):

∼

αgk

(

T

)

64µc

. (3.88)

166 Energy transfer processes in planetary bodies

The right-hand side of this equation can be written in terms of the Rayleigh number (equation

(3.62)) and a combination of dimensional parameters. After a bit of algebra and using the

definition of heat diffusivity we find that (3.88) can be simplified to:

q ∼ 0.25Ra

1/3



T



(3.89)

or in non-dimensional form (see equation (3.65)):

Nu∼ 0.25Ra

1/3

. (3.90)

From equation (3.65) we also see that the thickness of the thermal boundary layer is given by:

δ ∼ 4DRa

−1/3

. (3.91)

We can now substitute this value for δ in (3.85) to get the velocity:

u ∼0.25

2/3

. (3.92)

There are two implicit assumptions in this derivation. In the first place, it is assumed that

the thermal boundary layer is in steady-state thermal equilibrium with the interior of the

convective fluid. This means that the convecting fluid loses heat at the same rate as it is

conducted across the thermal boundary layer, as specified by equation (3.84). Second, we

assume that there is a source of energy for convection that supplies heat to the convecting

fluid at this same rate. Our derivation of the energy conservation equation, (3.83), specif-

ically rules out heat generation in the convecting fluid, so that the solution set given by

equations (3.89), (3.91) and (3.92) is strictly applicable only to a fluid layer heated from

below.

Worked Example 3.4 Archaean mantle convection

We will apply equations (3.89) through (3.92) to study how mantle convection may have

evolved throughout Earth’s history. One must keep in mind that these equations yield order of

magnitude estimates and not exact results, but because they rely on a single non-dimensional

parameter, the Rayleigh number, that encapsulates the dynamics of convection, they can

yield a high rate of return in terms of insight gained relative to effort invested.

Mantle convection may have differed in the distant geologic past because mantle

temperatures must have been higher than today’s (Chapter 2). Temperature enters into this

analysis in two ways: directly in the factor T and indirectly as a result of the temperature

dependence of viscosity. The viscosity–temperature function is discussed in Box 3.3.A

subtle but crucial point is that the temperature that enters into the calculation of viscosity

with equation (3.3.3) is a characteristic temperature of the interior of the fluid layer which is

not the same as the temperature at the bottom of the thermal boundary layer. The latter is the

one that defines the temperature contrast with the surface, T, that drives convection by

167 3.8 Parametrization of convection in planetary interiors

causing negative buoyancy. In a thick fluid layer such as a planetary mantle the two temper-

atures can be very different, owing to the adiabatic gradient. Moreover, temperature varies

across the convecting layer, so what is the characteristic value that we must use in order

to calculate viscosity with equation (3.3.3)? There is no unique answer to this question.

One possibility, which is what I have chosen to do here, is to use as characteristic mantle

temperature the temperature at a depth halfway across the fluid layer. Since the convecting

fluid lies on an adiabat, we can set the temperature at the base of the lithosphere, and then

calculate the temperature anywhere in the convecting layer by integrating equation (3.35).

The result is:

αg

(

y−y

)

, (3.93)

where T

is the temperature at depth y, and T

is the temperature at some reference depth

(e.g. the base of the lithosphere, but it could be anywhere else).

The results of parametrization of terrestrial mantle convection with equations (3.89)–

(3.92) is shown in Fig. 3.15 as a function of characteristic mantle temperatures (T

)

calculated with equation (3.93). The corresponding temperatures at the base of the litho-

sphere (T

) are shown in the bottom panel of the drawing. The temperature of the ocean floor

is close enough to 0

◦

C that we can assume that T

≈ T , as suggested in the figure. The

characteristic mantle temperature for the present day Earth’s mantle according to Schubert

et al. (2001) is 1950 K, shown with a thick broken vertical line in Fig. 3.15. This corresponds

to a temperature at the base of the lithosphere of ∼1400

◦

C, which is consistent with petro-

logic constraints (Chapter 10). The bottom panel of the figure also shows mantle viscosities

calculated with equation (3.3.3), using a reference viscosity of 10

Pa s at 1950 K and an

activation energy of 300 kJ mol

−1

(see Box 3.3 and Chapter 12). Other model parameters

are listed in the figure caption.

Our first task is to gauge the performance of the model against the terrestrial mantle

that we can observe today. The parametrized model predicts a present-day mantle heat flux

of ∼82 mW m

−2

, a convection velocity of ∼15 cm yr

−1

, and a lithospheric thickness of

∼50 km. The predicted heat flux corresponds almost exactly (and probably fortuitously) to

the observed heat loss that can be attributed to the spreading–subduction cycle (Box 3.2).

Agreement is less good for the other two parameters, which are off by a factor of approx-

imately 2 (observed values are 5–10 cm yr

−1

and ∼100 km), but certainly of the correct

order of magnitude.

What can we infer about the Earth’s mantle in the distant geologic past? Petrologic

evidence (e.g. eruption of ultramafic lavas such as komatiites) and models of the Earth’s

thermal history suggest thatArchaean mantle temperatures may have been 200–400 K higher

than today’s. The model then suggests that Archaean mantle heat flux may have been about

3–4 times higher than today’s, plate thicknesses may have been about half of today’s, and

convection velocity may have been up to one order of magnitude faster, maybe approaching

1 meter per year! Plate tectonics, in the sense of mantle convection with a mobile thermal

boundary layer, almost certainly existed, for the processes that make it possible – breaking

and bending of plates – are facilitated by a thinner lithosphere (see next section). But owing

to their lesser thickness (and hence rigidity) Archaean plates must have been smaller, and

therefore more numerous, than today’s, and may have moved up to ten times faster. The total

length of plate margins, convergent and divergent, would therefore have been greater than