Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

188 The Second Law of Thermodynamics

the system is not an adiabatic one, and entropy generation accompanies heat transfer, as in

equation (4.5).

There is also the issue of where the work performed by the quasi-static expansion goes.

When a system expands quasi-statically it performs work on its environment. This must be

so if we are to allow for an infinitesimally slow expansion. It would be in principle possible

to store the full amount of this mechanical energy in some device, such as by compressing

a spring or lifting a weight suspended from a cord running over a pulley. If we could com-

pletely eliminate friction then there would be no energy dissipation and releasing the spring

or the weight at an infinitesimally slow rate would compress the substance adiabatically to

its initial state. This is the meaning of a reversible transformation: one in which there is no

conversion of mechanical energy to heat (i.e. no dissipation). The three conditions: (i) no

entropy generation (dS = 0), (ii) no energy dissipation and (iii) reversible transformation

are thus equivalent. It would also be possible to make the quasi-static expansion in (a)

take place by adjusting a frictional force so that expansion proceeds infinitesimally slowly

by dissipating energy. Equation (4.19) would still be true for the expansion process, but

entropy would be generated by frictional dissipation somewhere else, and the entropy of

an isolated system large enough to contain all of the required components (“the Universe”)

would increase.

Let us now examine transformation (b). By hypothesis the system does not perform

external work during free expansion, because it is not expanding against any external force.

Let us assume for the sake of argument that the system is an ideal gas, so there are no

intermolecular forces and there is no work performed in separating the molecules either.

Then, from (4.16):

free expansion

=0. (4.20)

If after the free expansion is completed we wait long enough for the system to attain thermal

equilibrium (i.e. for all its molecules to “communicate” with one other and establish the

equilibrium velocity distribution) then we can substitute (4.12)in(4.20):

TdS

free expansion

−PdV =0 (4.21)

or:

free expansion

dV . (4.22)

For expansion dV > 0, and P and T are always positive quantities, so:

free expansion

> 0. (4.23)

Equation (4.23) says, for instance, that a gas will always expand to fill any empty space

available to it (“nature abhors a vacuum”), and it also says that a gas will never spontaneously

contract.

What is the physical meaning of the difference between equations (4.19) and (4.23)?

During free expansion the system does not perform mechanical work, as it is not expanding

against an external force, but rather just filling empty space (recall that we ignore inter-

molecular forces). The entropy increase measures the magnitude of the mechanical work

that could have been performed by the expansion, but wasn’t. When the system is in its

initial state, occupying volume V

, it has the capability of performing the amount of work

189 4.5 Planetary convection and Carnot cycles

that it performs during a quasi-static expansion. When we allow it to expand freely this

capability is irretrievably lost. This is equivalent to saying that the system initially stores

some amount of “potential for doing work” (careful! do not confuse this with potential

energy as defined in Chapter 1) that was dissipated when it expanded without performing

any work. From (4.21) we see that the integral of TdS is the amount of mechanical energy

that was lost, or dissipated, during the free expansion. This also shows that dW =PdV only

for a reversible transformation. For the irreversible free expansion dW = 0, but PdV =0.

The derivation of equation (3.32) for planetary adiabats assumes that the process is

isentropic, i.e. that no energy dissipation takes place. If energy dissipation takes place

during adiabatic expansion or compression then additional terms must be added to equation

(3.32) to account for this thermal energy. This is the reason why (3.32) is rigorously an

isentrope, which is a special case of an adiabat. We return to this in Chapter 10.

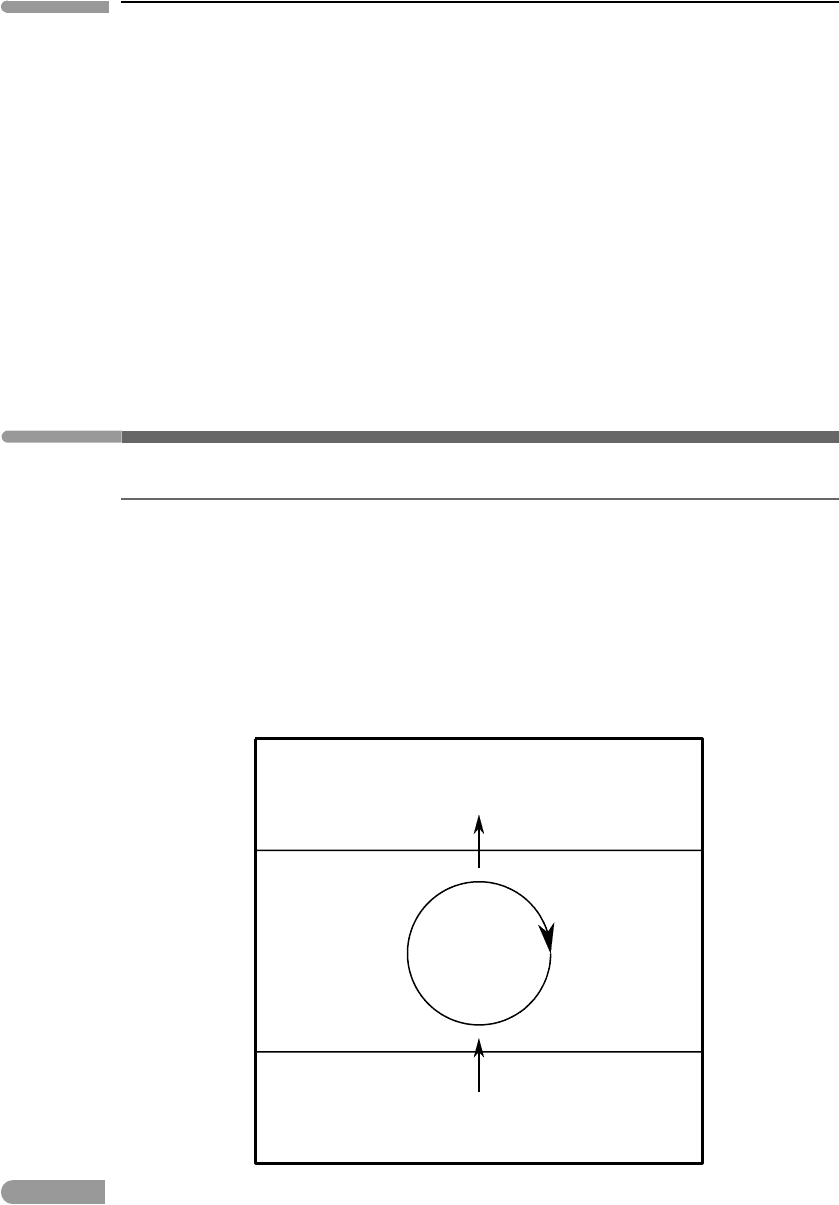
4.5 Planetary convection and Carnot cycles

4.5.1 Thermodynamic efficiency

A temperature gradient represents a potential for doing work. If heat is allowed to diffuse

without performing work then the loss of this work potential is energy dissipation, which

is measured by the amount of entropy that is generated. Consider a system bound by two

isothermal boundaries at different temperatures, T

, where the temperatures are held

constant by a heat source at temperature T

and a heat sink at temperature T

(Fig. 4.3). This

is a reasonable approximation for atmospheric convection, in which the planet’s surface is

the heat source and space is the heat sink. We can arrange for our idealized atmosphere

Heat source

Heat sink

Convection

Fig. 4.3

Idealized view of convection in a planetary atmosphere as a Carnot heat engine.

190 The Second Law of Thermodynamics

together with its heat source and its heat sink to make up an isolated system (this could

be the universe). Let the source at temperature T

transfer heat to the atmosphere at a rate

(−q

) < 0, where q = dQ/dt. Assume initially that heat diffuses across the atmosphere,

so that no work is performed. The atmosphere then delivers heat at the same rate rate q

the sink at temperature T

. Entropy generation is in this case maximum because no work is

being performed, so that the maximum rate of entropy generation, (dS/dt)

max

, is given by:





max

−q

−T

> 0. (4.24)

Now suppose that the atmosphere convects. In this case it performs work, which appears

as kinetic energy of moving air. The ideal maximum possible rate at which the atmo-

sphere can perform work must be such that the there is no entropy generation, so we make

(dS/dt)

min

=0, although in nature we never get this close (more on this soon). In this case

part of the heat flow q

is converted to work at a rate w

max

=(dW/dt)

max

, so that the rate

of heat loss across the top boundary, q

, is given by:

−w

max

. (4.25)

We can then write the minimum rate of entropy production as follows:





min

−q

−

max

−T

−

max

=0. (4.26)

Using (4.24), the maximum rate at which work can be performed is given by:

max





max

, (4.27)

which re-states the concept that entropy production measures the loss of work potential

(Section 4.4). Let us now define the thermodynamic efficiency of convection, η, as the ratio

of this maximum rate of performing work to the rate of heat absorption from the source, i.e.:

η =

max





max

. (4.28)

Substituting (4.24) and simplifying, we find:

η =1 −

. (4.29)

This result is originally due to the early nineteenth century French scientist Sadi Carnot,

although he was talking about steam engines and not planetary atmospheres. It is rightly

considered one of the cornerstones of thermodynamics, as it is what set Clausius and Kelvin

on the path to formalizing the Second Law of Thermodynamics.

Recall that in Chapter 3 we defined a heat engine as a thermodynamic cycle that converts

thermal energy to mechanical energy continuously and indefinitely. A planetary mantle or

atmosphere, or a steam engine, are heat engines, and equation (4.29) states that the (ideal)

maximum thermodynamic efficiency possible for a heat engine, called the Carnot efficiency,

depends only on the ratio between the temperature of the heat sink and the temperature of the

heat source. This is true for any heat engine, as in deriving (4.29) we made no assumptions

191 4.5 Planetary convection and Carnot cycles

whatsoever about the nature of the process by which some of the heat absorbed from the

source is transformed to mechanical energy.

There are two corollaries that follow from equation (4.29). First, the thermodynamic

efficiency is always less than 1, as T

=0 would require either a sink at absolute zero or

an infinitely hot source, and both are impossible (we will return to this when we discuss the

Third Law of Thermodynamics later in this chapter). Since η < 1, even if we could construct

a heat engine in which all friction and all other sources of dissipation are eliminated we

would still not be able to achieve complete conversion of thermal energy to mechanical

energy. The second corollary is that, if T

, then η =w

max

=0. This result is called the

Kelvin–Planck statement of the Second Law: it is not possible to construct a heat engine

that performs work by extracting heat from a single source at a constant temperature. Recall

that most of the mechanical energy generated in planetary mantles and cores is dissipated

by a combination of viscous and ohmic heating. Consider a hypothetical planet in which

there is neither tectonic nor magnetic work. If it were not for the Second Law all that we

would need for the mantle or core of such a planet to convect would be an initial supply

of heat and perfectly insulating boundaries. Once convection starts it would feed on heat

generated by its own dissipation. This is called a perpetual motion machine of the second

kind, and is impossible by (4.29) (or, more generally, by the Second Law).

4.5.2 Carnot’s cycle

As it turns out, it is possible to get a bit more specific about the type of heat engine that

achieves the maximum thermodynamic efficiency given by (4.29), and the result is relevant

to planetary convection. There are several ways of demonstrating what follows, which is

known as Carnot’s theorem. I think that this derivation, modified from Guggenheim (1967),

is particularly simple. Suppose that our heat engine absorbs heat at various temperatures,

, of which T

is the maximum, and releases heat at various temperatures T

, of which

is the minimum. Let the various rates of heat absorption and emission be q

and q

respectively, where, as in Section 4.5.1, all of the qs are positive quantities. The maximum

thermodynamic efficiency is always obtained when (dS/dt)

min

= 0. We now write this

condition with the following general equation ((4.26) is a special case of this equation, for

a single input and a single output temperature):





min

=−



=0, (4.30)

which we rewrite as follows:



. (4.31)

The rate at which work is performed is given by (compare (4.25)):

w =



−



(4.32)

and the thermodynamic efficiency by (see also (4.28)):

η =



=1 −



. (4.33)

192 The Second Law of Thermodynamics

The thermodynamic efficiency η is maximum when the ratio



is minimum. In

order to minimize this ratio we have to make each q

as small as possible, and each q

large as possible. By (4.31), we will accomplish this by making all T

equal to the minimum

value, T

, and all T

equal to the maximum value, T

. Thus, η takes its maximum possible

value, given by equation (4.29), when the heat engine absorbs heat at a single maximum

temperature, and releases heat at a single minimum temperature. The most efficient cycle

is one that works between two isothermal boundaries, with no heat exchanged at any other

temperature. Changes in the system that take place between the two isothermal boundaries

are therefore adiabatic.

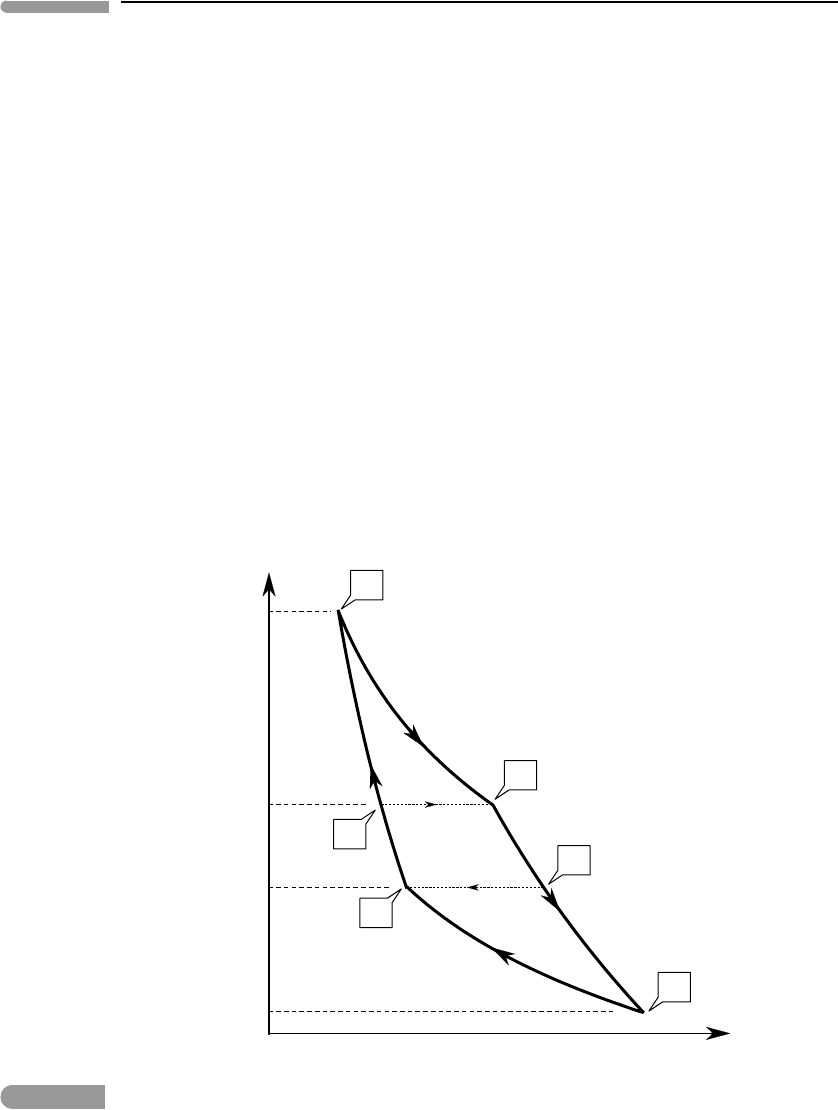
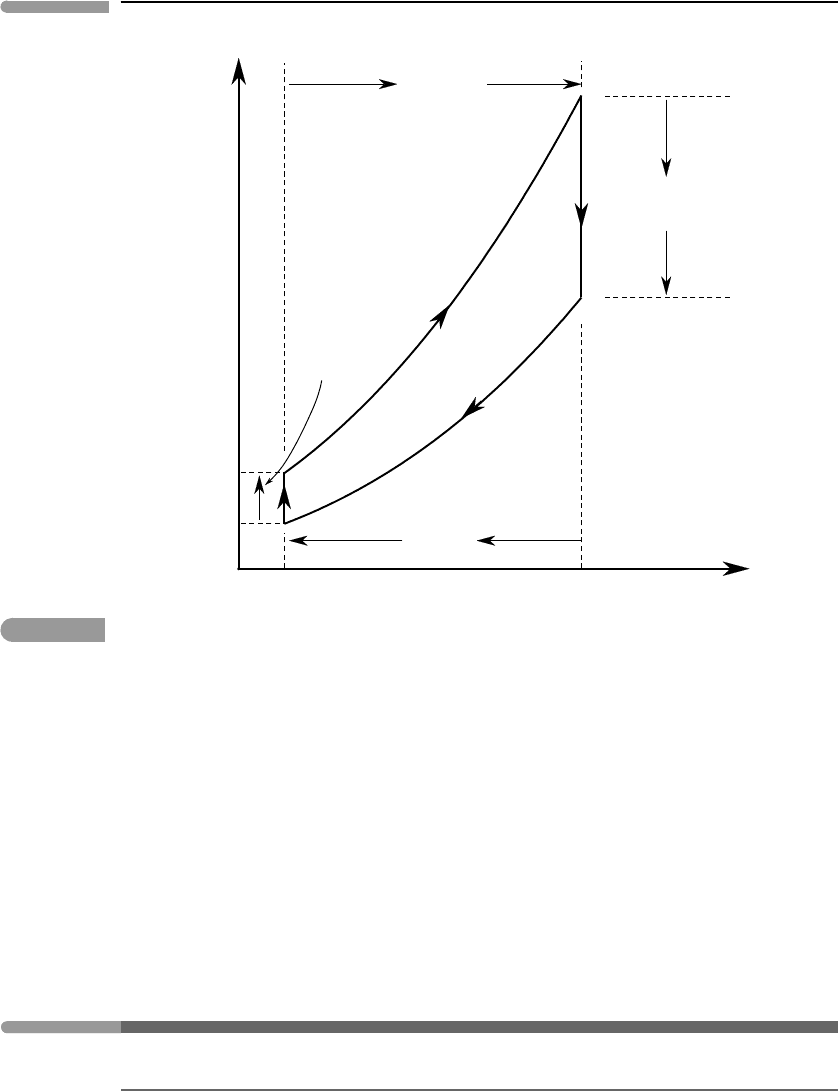
A thermodynamic cycle that is bound by two adiabats and two isotherms is called a

Carnot cycle. It is sketched in terms of its pressure–volume evolution in Fig. 4.4, where it

is compared to the isobaric–adiabatic cycle that I proposed as a model for mantle convec-

tion in Section 3.4. Carnot’s cycle operates between two temperatures, T

, which are

re-labeled T

and T

, respectively, for comparison with Fig. 3.9. Starting from the high-

est pressure point in the diagram (P

), the fluid in Carnot’s cycle absorbs heat at constant

temperature T

, expanding (performing work) and decompressing to P

. From this point

the fluid expands adiabatically and cools down, until it reaches temperature T

at pressure

. It then releases heat at constant temperature T

, so that it contracts and its pressure

increases to P

, from which point the fluid is compressed adiabatically until it reaches the

isotherm

adiabat

Fig. 4.4

The mantle convection cycle proposed in Chapter 3: isobaric heating at the core–mantle boundary from T

to T

adiabatic decompression during mantle upwelling from T

to T

, isobaric cooling at the surface from T

to T

, and

adiabatic compression during mantle downwelling from T

to T

(the isobaric legs are shown with thin dotted lines).

Mantle convection approximates a Brayton cycle, that is compared in the ﬁgure to a Carnot cycle working between the

same extreme temperatures, T

and T

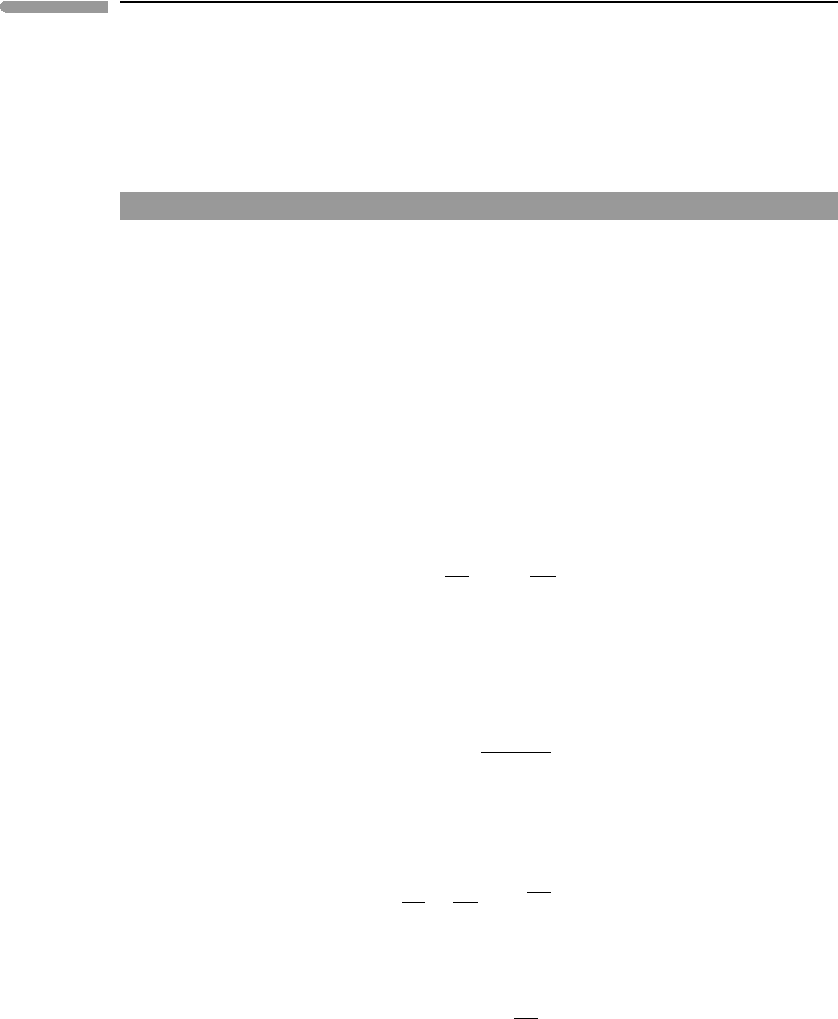
193 4.5 Planetary convection and Carnot cycles

initial state, at temperature T

and pressure P

. If the cycle is completed in unit time then

the area bound by the four curves is the working rate, w. According to equation (4.29), as

the two isotherms become further apart the efficiency of conversion of thermal energy to

mechanical energy (η) increases. Convesely, if T

then it must be η = 0.

Worked Example 4.2 Efficiency of planetary convection systems

In contrast to Carnot’s cycle, the convection cycle in Section 3.4 absorbs enthalpy at constant

pressure, between temperatures T

and T

, and releases enthalpy at constant pressure,

cooling from from T

to T

at the planet’s surface (see Fig. 4.4). Such an isobaric–isothermal

cycle is called a Brayton cycle or Joule cycle, and, interestingly, it is also an approximate

description of the working of jet engines. We have just proved that, given that in this case

heat is absorbed and released over a range of temperatures, the thermodynamic efficiency of

convection in planetary interiors must be less than the efficiency of a Carnot cycle working

between the same extreme temperatures, T

and T

, given by (4.29) (see Figs. 3.8, 3.9

and 4.4). We will now calculate the thermodynamic efficiency of the Brayton cycle. Let

be the rate of heat absorption at high pressure (from T

to T

) and q

be the rate of

heat release at low pressure (from T

to T

). Work is performed at a rate w =q

−q

,so

that the thermodynamic efficiency of the Brayton cycle, η

, is given by (compare equation

(4.28)):

=1 −

. (4.34)

For notation simplicity we will take the unit of time as being equal to the cycle’s period. Then,

given that the two heat transfer legs of the cycle are isobaric, we have q

= c

−T

)

and q

= c

−T

), where we have arranged for all the qs to be positive quantities.

Substituting into (4.34):

=1 −

−T

. (4.35)

Note that T

and T

lie on the same adiabat, and so do T

and T

. Assuming that the

adiabats are also isentropes we can write the temperature ratio as a function of the thickness

of the convecting layer, D, by integrating (3.35), as follows:

−

αgD

. (4.36)

Substituting in (4.35) we get an estimate for the thermodynamic efficiency of convection

in planetary interiors:

=1 −e

−

αgD

. (4.37)

The exponent (αgD)/c

is a non-dimensional parameter that is a function of material

properties, gravitational acceleration and thickness of the convecting layer, but not of

temperature, except indirectly through the effect of T on α.

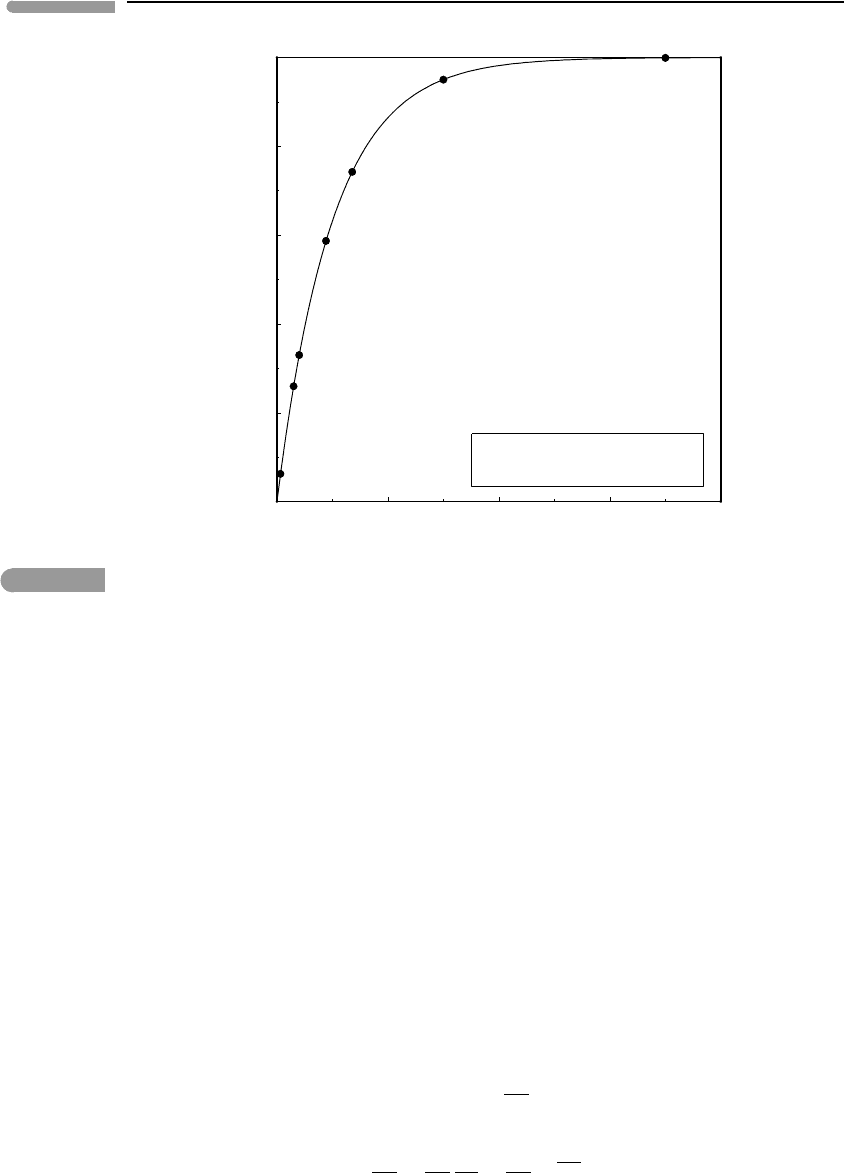
We can use equation (4.37) to compare the thermodynamic efficiency of convection in

planetary interiors. Figure 4.5 shows the function η

=1−e

−x

(equation (4.37)) and rough

estimates of the value of the exponent x =(αgD)/c

for various planetary bodies. A small

194 The Second Law of Thermodynamics

0246

0.2

0.4

0.6

0.8

(gα

D)/C

Earth’s mantle

Martian mantle

Saturn

Jupiter

Earth’s core

Uranus

Neptune

Thermodynamic efficiency of

planetary convection

Fig. 4.5 Thermodynamic efﬁciency of the Bryton cycle as a model for convection in planetary interiors. Values for giant planets

are very rough approximations, calculated with the assumption of very simple internal structures and equations of

state, and assuming constant g. The correlation of greater efﬁciency with larger size is likely to be qualitatively correct.

planet such as Mars is not efficient at transforming thermal energy into mechanical energy.

Even at an early age, when its internal heat flow may have been significantly higher than

today’s terrestrial heat flow, it is unlikely that Mars could have supported a rate of tectonic

activity comparable to Earth’s plate tectonics. In contrast, the giant planets, by virtue of their

large sizes, can be very efficient heat engines. Convection of ionized fluids in their interiors

is thought to be responsible for their magnetic fields (Section 1.8.3). Efficient conversion

of their high heat flows to mechanical energy may be an important factor in explaining the

strong magnetic fields of the giant planets. Of course, Fig. 4.5 shows only thermodynamic

efficiencies, and only a very small fraction of the work performed by convection leaves the

planetary interior as mechanical energy, for example, in the form of lithospheric deformation

or planetary magnetic fields. Most of the mechanical energy is dissipated by viscous flow

and electric currents (see also Section 1.8.3), and leaves the planetary interior as heat. The

actual efficiency of convection in planetary interiors is close to 0, and the rate of entropy

generation is close to the maximum given by equation (4.26).

We can also show that the thermodynamic efficiency of the convection cycle, given by

equation (4.37), is less than that of a Carnot cycle working between the same extreme

temperatures (Fig. 4.4) and given by equation (4.29):

=1 −

. (4.38)

We can write this temperature ratio as follows (see equation (4.36)):

−

αgD

. (4.39)

195 4.5 Planetary convection and Carnot cycles

Calling T = T

−T

we write the efficiency of the Carnot cycle as:

=1 −e

−

αgD

T

−

αgD

, (4.40)

which leads to:

=η

−

T

−

αgD

(4.41)

or, in other words, η

< η

, as required by Carnot’s theorem.

Equation (4.41) has an interesting implication. This is that, as T becomes smaller, the

thermodynamic efficiency of the Brayton cycle approaches that of the Carnot cycle. This is

immediately obvious from Fig. 4.4:asT becomes smaller, the adiabatic excursions needed

to construct a Carnot cycle between the same extreme temperatures become smaller and the

two cycles become more similar. However, from Fig. 3.9 and our discussion of convection

in Chapter 3, we recall that T is the temperature contrast that drives convection. We must

therefore conclude that the thermodynamic efficiency of stagnant lid convection is closer to

the maximum Carnot efficiency than that of convection with moving plates. This may seem

counterintuitive, for example in view of the fact that Earth has a more active lithosphere

than Venus. But one must not confuse efficiency with the actual rate of performing work.

The rate at which the convection cycle performs work is given by:

w =q

−q

[

(

−T

)

−

(

−T

)

]

(

−T

)



αgD

−1



, (4.42)

which, for a given planetary size (constant g and D), yields:

w ∝T . (4.43)

Plate tectonics is driven by a greater temperature contrast than stagnant lid convection, so

it performs mechanical works at a greater rate than the latter.

Atmospheric circulation over tropical and subtropical oceans approaches a Carnot cycle

more closely than convection in planetary interiors. This is particularly striking in the case

of hurricane formation (see Emanuel, 1986, 2006), but we can also see Carnot at work in

Earth’s global climate patterns. Because of the immense heat capacity of the oceans, air

absorbs heat and humidity from tropical oceans at their (nearly) constant surface temper-

ature, T

, causing atmospheric pressure to decrease from P

to P

(Fig. 4.6). When the

density has decreased sufficiently it rises and cools adiabatically from T

to T

, causing con-

densation and precipitation in the tropics. As air moves towards higher latitudes it radiates

heat to space at the approximately constant temperature of the tropopause (troposphere–

stratosphere boundary), T

. Air density thus increases isothermally from P

to P

, at which

point it becomes negatively buoyant and sinks.Adiabatic compression raises its temperature

from T

to T

. This hot and dry sinking air gives rise to the belts of subtropical deserts on

both sides of the equator.

To calculate the Carnot efficiency of atmospheric convection we integrate (3.36)as

follows:

=1 −

, (4.44)

196 The Second Law of Thermodynamics

Air moves over ocean

from subtropics

towards equator

Air rises

at equator

Air sinks

in subtropics

Air moves

at altitude

towards subtropics

Fig. 4.6

Highly idealized view of atmospheric convection in the tropics as a Carnot engine. Air absorbs heat isothermally from

the oceans and releases heat isothermally to space. The large thermal effect of condensation during adiabatic rise

near the equator is ignored in the ﬁgure. For a rigorous discussion see Emanuel (1986, 2006).

where h is the thickness of the troposphere, ∼10 km and T

is a characteristic surface

temperature, ∼300 K. With these values we obtain η ≈ 0.3 for the terrestrial atmosphere.

This would appear to suggest that atmospheric convection is able to convert about a third

of the thermal energy that it absorbs from the Earth’s oceans into mechanical energy. But of

course this is not quite so, because the thermodynamic efficiency given by equation (4.44)

does not take into account dissipation in the engine itself, i.e. the finite viscosity of air (see

Section 3.7.4) and friction at the interface between the atmosphere and the Earth’s surface.

The effective efficiency of atmospheric convection is much lower than 0.3.

4.6 A microscopic view of entropy

4.6.1 Microstates and macrostates

Entropy, like internal energy, is a macroscopic variable. It allows us to make accurate

predictions about natural processes and, in regards to much of the material that we will

cover in this book, the macroscopic understanding of entropy is all that we need. There are,

however, some topics, such as solid solutions (discussed in Chapter 5) and equations of

197 4.6 A microscopic view of entropy

state (discussed in Chapters 8 and 9) for which it is useful to have an understanding of the

microscopic underpinnings of entropy. In addition to this practical reason, there is a more

fundamental one. We saw in Section 1.14 that internal energy, the macroscopic concept that

forms the basis for the First Law, has a well-defined microscopic interpretation. It would be

deeply unsatisfactory if the same were not true of entropy, which is at the core of the Second

Law. There is also much misuse and abuse of the word entropy by non-scientists and pseudo-

scientists, and for this reason too it is important to have a deeper understanding of what it is.

The microscopic interpretation of entropy begins with the concepts of the microstate of

a system vs. its macrostate. The macrostate of a system is defined solely on the basis of

macroscopic variables and does not require knowledge of the underlying microscopic con-

figuration of the system, which is what we call its microstate. For example, the macrostate

of an ideal gas made up of a single chemical species is fully specified by its temperature

and its pressure, from which we can calculate all of its other macroscopic parameters, such

as molar volume, internal energy, enthalpy and entropy (we shall see how). Although this

macroscopic specification of the sate of a system is independent of any knowledge of its

underlying microscopic structure, in Section 1.14 we saw that we can also define the internal

energy of an ideal gas in terms of a microscopic model called the kinetic theory of gases. In

order to describe the microstate of a system made up of ideal gas we would need to specify

the position and velocity of each of the individual molecules. Here lies the crucial differ-

ence between macrostates and microstates: a given macrostate may arise from more than

one different microstate. For example, we know that the distribution of molecular speeds

is as given by Fig. 1.12, but there are many ways in which 10

individual molecules may

arrange themselves to give this distribution (see Box 4.1). Each of these different ways is

a microstate. As far as the macrostate is concerned we don’t care what the velocity of each

individual molecule is, i.e. which specific equivalent microstate we have, as long as the

velocity distribution is the one that corresponds to that specific macrostate.

Box 4.1

Counting microstates

The microscopic interpretation of entropy, and indeed much of statistical mechanics, relies on being able to

count the number of equivalent microstates. We deﬁne all microstates that give rise to the same macrostate

as being equivalent. Consider a situation in which there are N objects of the same kind, each of which can

exist in i different states, with N ≥i. For example, it could be a group of N coins, each of which can be in one

of two states (heads or tails), or a group of N octahedral sites in a crystal of olivine, each of which can be in

one of two states (ﬁlled with Mg or Fe

), or a group of N particles in a gas, each of which can be in one of i

different energy levels. We want to know how many possible microstates these systems have. A microstate

is deﬁned by the number of objects that are in each possible state. All microstates with the same number of

objects in each state are equivalent and correspond to the same macrostate. For example, if we have 5 coins,

then all microstates with 3 heads and 2 tails are equivalent, and correspond to a single macrostate that is

different from the one that arises from all microstates in which there are 4 heads and 1 tail. We wish to

calculate the number of equivalent microstates that underlie a given macrostate.

The total number of arrangements of the N objects, which you can think of as the number of ways in

which we can choose them one at a time, is N!: we can choose the ﬁrst in N ways, the next in (N −1)

ways, the next one in (N −2) ways, and so. You can visualize this process as arranging the objects in a

row, but this is just a help in visualization and has nothing to do with any putative spatial distribution of the

objects. We thus have N! possible arrangements of objects (e.g. coins), and each object can be in one of i

different states (e.g. heads or tails). Let n

be the number of objects that have the property i, i.e. that are in