Douce A.P. Thermodynamics of the Earth and Planets
Подождите немного. Документ загружается.


218 The Second Law of Thermodynamics
4.8.4 Conjugate variables, extensions and transformations of the
thermodynamic potential
Each of the pairs of variables that appear in the fundamental equation (4.101): P –V , T –S,
µ–n, are called conjugate variables and have some important regularities. First, and obvi-
ously, their product in every case has dimension of energy. Second, each conjugate pair
consists of an intensive variable (P , T , µ) and an extensive variable (V , S, n). Third, in
every case the intensive variable is a “driving potential” for “displacement” of the extensive
variable: a pressure gradient causes a change in volume, a temperature gradient causes heat
flow and hence a change of entropys and a gradient in chemical potential causes diffusion
of chemical components and hence a change in mol numbers. Each of the three products of
conjugate variables tracks a separate contribution to the thermodynamic potential: expan-
sion work, heat transfer and mass transfer. We now see that adding the compositional term
(µdn) to (4.12) in order to obtain (4.101) consisted of adding the product of a pair of
conjugate variables that accounts for the energetic contribution of chemical composition to
the thermodynamic potential E. There is no reason why we should stop here. Suppose that
we are interested in a system in which mechanical work is also performed. We then need to
add the product of an intensive variable that measures a “driving potential”, in this case a
force F, times its extensive conjugate, which is the distance over which the force acts, dx.
The fundamental equation for E then becomes:
dE =TdS −PdV +
i
µ
i
dn
i
+Fdx. (4.105)
Other terms could be added if we were also interested in the work of, for example, grav-
itational forces, elastic forces, Lorentz forces or nuclear forces. Once we identify all of
the energetic contributions to the thermodynamic potential we are free to add or remove
products of conjugate variables as needed.
Each of the terms in equations (4.101)or(4.105) is the product of an intensive variable
times the differential of its extensive conjugate. In other words, if we restrict ourselves to
equation (4.101) then internal energy is a function of the form E = E (S, V , n
i
). This
raises the question, is this the only way of writing a thermodynamic potential? Could we
define a thermodynamic potential in which the natural variables are intensive variables, so
that the minimum energy condition can be applied to a system in which intensive variables,
such as P and T, are held constant? On dimensional grounds all we can expect is that a
thermodynamic potential must be a sum of products of conjugate variables. In each of the
products, however, either of the two variables could be the one that appears in differential
form. Consider some other function, say Y = Y (T ,V ,n
i
), or any other combination of
variables that are not conjugate among themselves. Do such functions exist? And do they
have the properties of thermodynamic potentials?
4.8.5 The Legendre transform
The answer to the questions in the last paragraph is yes, but we have to be careful with how
we construct these other functions. In order to ensure that any new function that we construct
is a thermodynamic potential we must begin with a thermodynamic potential, such as E =
E (S, V , n
i
), and transform this function in such a way that all of its properties are inherited
by the new function. This is accomplished by means of a mathematical procedure called

219 4.8 Thermodynamic potentials
the Legendre transform. The Legendre transform is in essence a change of coordinates. We
choose any (or all) of the coordinates of the original function (its natural variables) that are
not convenient for our purposes, and find a new function that contains the same information
in terms of the conjugates of the original coordinates, which become the natural variables
of the new function.
Suppose you have a function φ(x), and that its natural variable x is a physical quantity
that is hard to measure and/or that is difficult to control. The first derivative of φ: dφ/dx,
is, however, a physical quantity that is easy to handle. By this I mean that it is easy to
come up with natural situations in which dφ/dx stays constant, and also that dφ/dx is easy
to measure. Call this quantity dφ/dx = y. It would be useful if we could construct a new
function, ψ(y), that contains the same information as φ, but that is a function of y rather than
x. An example is internal energy. Entropy is one of the natural variables of E, but entropy
is a physical quantity that cannot be measured directly. We thus have the easy-to-define but
hard-to-work-with function E(S). Its first derivative, (∂E/∂S)
V
=T (equation (4.103)) is,
however, a physical quantity that is easy to measure and is intuitively easy to grasp. We
seek another function that contains the same thermodynamic information as E, but that is
written in terms of T as one of its natural variables, instead of its conjugate S.
The Legendre transform allows us to do this for certain types of function. The concept
of the Legendre transform is best approached geometrically (Fig. 4.12). The key idea is
φ(x)
φ
ψ
x
yx
y = dφ /dx
Fig. 4.12
Geometric interpretation of the Legendre transform. If a function is strictly convex, meaning that its second derivative
does not change sign such as φ(x) in the figure, then the function can also be described by the set of all of its tangent
lines. The value of the primitive function is given by φ =yx +ψ, where y is the slope of the tangent line at x. Note
that ψ(y) is the Legendre transform of φ(x), given by ψ(y) = φ(x) −yx.

220 The Second Law of Thermodynamics
that the set of all tangent lines to the curve φ(x) describes the function φ(x) as well as the
function itself. This only works if there is a one-to-one relationship between x and y or, in
other words, if each value of the slope y occurs at one and only one value of x. This is the
case for the function shown in the figure. It means that x is a function of y, i.e. x = x(y).
The converse is necessarily true if φ is a function of x. A function for which there is a
one-to-one correspondence between the independent variable, x, and the slope, y, is called
strictly convex and is characterized by the fact that its second derivative never changes sign.
Equations (4.103) and (4.104) show that this is the case for the natural variables of internal
energy, so the Legendre transform can be applied to E.
From Fig. 4.12 it is clear that we can write ψ as follows:
ψ =φ −yx. (4.106)
So as to keep track of the fact that the function that we seek is a function of y, we write
(4.106) more completely as follows:
ψ(y) =φ(x(y)) −yx(y), (4.107)
where the convexity of φ guarantees that the function x(y) exists. Equation (4.107)isthe
Legendre transform of φ: it transforms the function φ(x) into the functionψ(y), that contains
the same information as φ, but now in terms of our preferred variable y. In particular,
the Legendre transform switches the roles of the conjugate variables in thermodynamic
functions. From the definition of y =dφ/dx we have:
dφ = ydx. (4.108)
Differentiating ψ relative to y in equation (4.106):
dψ
dy
=
dφ
dx
dx
dy
−y
dx
dy
−x =y
dx
dy
−y
dx
dy
−x =−x (4.109)
or:
dψ =−xdy. (4.110)
If φ is a function which has x as one of its natural variables, the ψ is another function for
which y, which is the conjugate of x, is a natural variable.
We need to demonstrate that if φ is a thermodynamic potential, then ψ is also a thermo-
dynamic potential. First we note that the Legendre transform conserves the convexity of
the function, as we can easily see from:
d
2
ψ
dy
2
=
d
dy
dψ
dy
=−
dx
dy
=−
1
d
2
φ
dx
2
. (4.111)
This says that, if the second derivative of φ does not change sign (φ is strictly convex), then
the second derivative of ψ does not change sign either, and it is strictly convex too. From
here it is simple to show that the Legendre transform is invertible, and that the Legendre
transform of ψ is φ (exercise left to the reader).
Suppose now that φ is a thermodynamic potential. This means that in a system in which
its natural variables are held constant φ takes a minimum value at equilibrium. As usual we
track the behavior of the systems relative to an unspecified variable Z that can vary when

221 4.8 Thermodynamic potentials
some restriction is released. Recall that Z is not one of the natural variables of φ, but rather
a quantity that can vary while the natural variables of φ are held constant. For example, this
could be the progress of a chemical reaction towards equilibrium measured by the amount
of matter that reacts, or the progress of a system towards thermal equilibrium measured by
the amount of heat transferred. It is not necessary to specify what the variable Z actually
is. We write the equilibrium condition for the thermodynamic potential φ as follows (see
equations (4.84), (4.85) and (4.92), (4.93)):
∂φ
∂Z
x
=0 (4.112)
∂
2
φ
∂Z
2
x
> 0, (4.113)
where for simplicity we consider only one natural variable, x. From equation (4.106)we
find the derivative of ψ at constant value of its natural variable, y:
∂ψ
∂Z
y
=
∂φ
∂Z
y
−y
∂x
∂Z
y
=
∂φ
∂Z
y
. (4.114)
The last identity in (4.114) comes from the fact that the following must always be true:
∂y
∂Z
x
=
∂x
∂Z
y
=0 (4.115)
given that, as x = x(y),ify is constant then x is constant, and conversely if x is constant
then y is constant. Using identities (1.3.12) and (4.115):
∂φ
∂Z
y
=
∂φ
∂Z
x
+
∂φ
∂x
Z
∂x
∂Z
y
=
∂φ
∂Z
x
, (4.116)
which substituting in (4.114) shows that:
∂ψ
∂Z
y
=
∂φ
∂Z
x
. (4.117)
This is true in general, and therefore also at an extremum at which (4.112) is valid. Therefore,
an extremum of the function φ is also an extremum of the function ψ. In order to prove that
ψ is a thermodynamic potential all we need to do is prove that this extremum is a minimum.
We take the second derivative of (4.106):
∂
2
ψ
∂Z
2
y
=
∂
2
φ
∂Z
2
y
−y
∂
2
x
∂Z
2
y
=
∂
2
φ
∂Z
2
y
, (4.118)
where the second identity follows from (4.115): derivatives of any order of y at constant x,
and of x at constant y, vanish. Switching the order of differentiation and applying identity

222 The Second Law of Thermodynamics
(4.116) repeatedly:
∂
2
φ
∂Z
2
y
=
∂
∂Z
∂φ
∂Z
y
y
=
∂
∂Z
∂φ
∂Z
x
y
=
∂
∂Z
∂φ
∂Z
y
x
=
∂
∂Z
∂φ
∂Z
x
x
=
∂
2
φ
∂Z
2
x
(4.119)
from which we conclude that:
∂
2
ψ
∂Z
2
y
=
∂
2
φ
∂Z
2
x
(4.120)
so, from (4.113), a minimum for φ is also a minimum for ψ. This completes the proof
that the Legendre transform constructs a new function that inherits its properties from
the primitive function. The Legendre transform of a thermodynamic potential is another
thermodynamic potential in which the roles of the conjugate variables have been switched.
The advantage of deriving this relationship in terms of a generic variable with the properties
of a thermodynamic potential is that the results are valid for any and all of the natural
variables of any thermodynamic potential. For functions of several variables, such as E =
E(S,V ,n
i
), we can transform as many or as few of the natural variables as we wish.
Relations (4.117) and (4.120) are true for every variable that we transform.
4.8.6 The four fundamental thermodynamic potentials
By means of the Legendre transform we can construct three other thermodynamic potentials
starting from E, by transforming each of its natural variables, S and V, separately, or both
of them simultaneously. Let H be the potential in which pressure replaces its conjugate,
volume, as a natural variable. By (4.107):
H
(
S, P , n
i
)
=E
(
S, V (P ),n
i
)
−V (P )
∂E
∂V
S, n
i
(4.121)
or, more compactly and using (4.104):
H
(
S, P , n
i
)
=E
(
S, V , n
i
)
+P V , (4.122)
which is identical to (1.59). Enthalpy is the thermodynamic potential which has entropy
and pressure as its natural variables. Using the notation of thermodynamics and substituting
(4.101) (compare equation (4.13)):
dH = dE +PdV +V dP = TdS +V dP +
i
µ
i
dn
i
. (4.123)
Enthalpy is the thermodynamic potential that allows us to define equilibrium at constant
pressure and entropy.
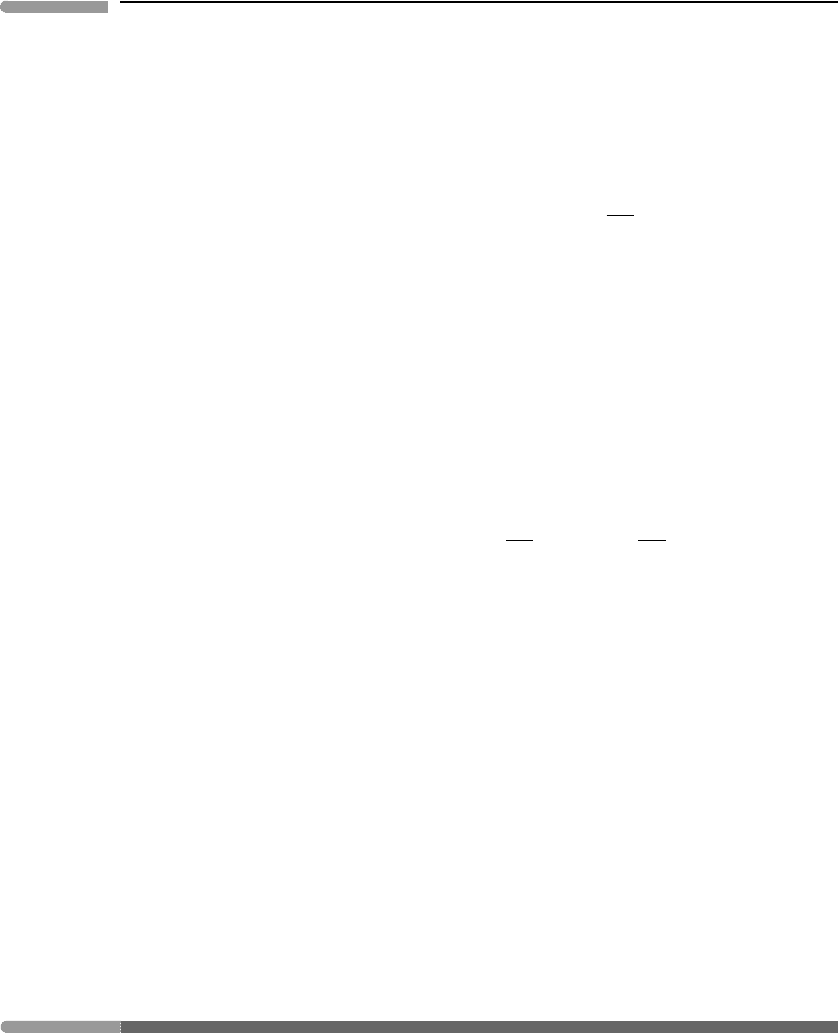
223 4.9 Gibbs free energy
In the study of equations of state (Chapters 8 and 9) it is convenient to work with
a thermodynamic potential that is a function of temperature and volume. This function is
called the Helmholtz free energy and is symbolized by F =F (T ,V , n
i
). Some authors use A
for this potential but I reserve A for a different function called the affinity (Chapter 12). The
Helmholtz free energy is the Legendre transform of internal energy relative to entropy, i.e.:
F
(
T , V , n
i
)
=E
(
S(T ),V , n
i
)
−S(T )
∂E
∂S
V ,n
i
(4.124)
or, using (4.103):
F
(
T , V , n
i
)
=E
(
S, V , n
i
)
−T S, (4.125)
which results in:
dF = dE −TdS −SdT =−SdT −PdV +
i
µ
i
dn
i
. (4.126)
A function that is central to much of chemical thermodynamics is the Gibbs free energy,
G = G(T , P , n
i
) which is the double Legendre transform of internal energy relative to
entropy and volume:
G
(
T , P , n
i
)
=E
(
S, V ,n
i
)
−S
∂E
∂S
V , n
i
−V
∂E
∂V
S, n
i
. (4.127)
Using (4.103), (4.104), (4.125) and (1.59) we find the following identities:
G =E −T S +P V
G =F +P V
G =H −T S.
(4.128)
In thermodynamics notation the total differential of Gibbs free energy in terms of its natural
variables is:
dG =−SdT +V dP +
i
µ
i
dn
i
. (4.129)
Other thermodynamic potentials are possible, by transforming any of the other conjugate
variables in (4.105), or any additional ones that we may need to add for any specific prob-
lem. In particular, potentials in which mol numbers n
i
are switched with their conjugates,
chemical potentials µ
i
, are known as grand thermodynamic potentials.
4.9 Gibbs free energy
Planetary bodies act as large reservoirs of thermal energy and mass that tend to buffer P
and T while chemical reactions take place, so that it is commonly a good approximation
to assume that natural chemical reactions occur at constant temperature and pressure. The
thermodynamic potential appropriate to studying equilibrium under these conditions is
therefore the Gibbs free energy, which has pressure and temperature as its natural variables
(equations (4.127) and (4.129)). Equilibrium in a system at constant pressure and constant

224 The Second Law of Thermodynamics
temperature is defined by the minimum value of its Gibbs free energy. In the differential
notation of thermodynamics we express this as follows:
dG
T ,P ,n
i
=0 (4.130)
d
2
G
T ,P ,n
i
> 0. (4.131)
A significant portion of the remainder of this book is focused on calculating Gibbs free
energy for a wide range of planetary materials over a wide range of pressures and temper-
atures. Minimization of Gibbs free energy is the fundamental mathematical tool used to
study chemical equilibrium. Here we focus on some general properties of the Gibbs free
energy function.
4.9.1 Derivatives of the Gibbs free energy
The first and second derivatives of G relative to its natural variables, P ,T and n
i
, show up
repeatedly in chemical equilibrium calculations, so we review them here. From (4.129)we
have the following first derivatives:
∂G
∂T
P ,n
i
=−S (4.132)
∂G
∂P
T ,n
i
=V (4.133)
∂G
∂n
i
T ,P ,n
j=i
=µ
i
. (4.134)
The chemical potential of component i is, thus, the first derivative of G relative to n
i
, taken
at constant T, P and mol numbers of all the other system components, n
j=i
. This definition,
which is the one that we will most commonly use in this book, is different from (4.102),
but the chemical potential is the same as the one defined there, and has the same value. The
second derivative relative to T is:
∂
2
G
∂T
2
P ,n
i
=−
∂S
∂T
P ,n
i
=−
C
P
T
, (4.135)
which relies on the definitions of entropy (equation (4.6)) and heat capacity at constant
pressure (equation (1.53)). We also have:
∂
2
G
∂P
2
T ,n
i
=
∂V
∂P
T ,n
i
=−V β
T
, (4.136)
where we have used the definition of isothermal compressibility, equation (1.65). Using the
definition of coefficient of thermal expansion, equation (1.66), the mixed second derivative
yields:
∂
2
G
∂P∂T
n
i
=
∂
∂T
∂G
∂P
T ,n
i
P ,n
i
=
∂V
∂T
P ,n
i
=V α. (4.137)
The three material properties that I defined in section 1.11, C
P
, β
T
and α, are simple
functions of the three second derivatives of Gibbs free energy. Other material properties

225 4.9 Gibbs free energy
such as heat capacity at constant volume, adiabatic compressibility and the Grüneisen
parameter are similarly related to the second derivatives of other thermodynamic potentials
(see Exercise 4.9).
A fundamental result of multivariable calculus says that, if a function complies with
certain requirements about continuity and differentiability (and thermodynamic potentials
do), then the order of differentiation in mixed second- and higher-order derivatives does
not matter. This means that we could have also written (4.137) as follows:
∂
2
G
∂P∂T
n
i
=
∂
∂P
∂G
∂T
P ,n
i
T ,n
i
=−
∂S
∂P
T ,n
i
, (4.138)
which results in:
∂S
∂P
T ,n
i
=−
∂V
∂T
P ,n
i
=−V α. (4.139)
Equation (4.139) is one example of a large number of analogous relationships, called
Maxwell relations, that can be obtained from the identity of mixed second derivatives of any
thermodynamic potential. These relations are sometimes tabulated, but I don’t see the point
of that, as they are very easy to derive starting from the definition of the thermodynamic
potential appropriate to the problem at hand (see Exercise 4.10). Maxwell’s relations are
often useful when solving problems in thermodynamics (e.g. Chapters 8, 9 and 10). They
are also used to derive thermodynamic identities as discussed in Appendix 2.
Worked Example 4.6 Isentropes and adiabats revisited
An example of the application of the derivatives of thermodynamic potentials is to find the
equation that describes P and T along an isentropic transformation. Consider an isentropic
transformation in a system in which the only intensive variables are P and T. This could
be, for instance, compression or expansion of a convecting fluid in a planetary mantle,
ocean or atmosphere. For a constant entropy transformation we have:
dS =
∂S
∂T
P
dT +
∂S
∂P
T
dP = 0. (4.140)
Substituting (4.135) and (4.139)in(4.140):
C
P
T
dT −V αdP = 0 (4.141)
or:
∂T
∂P
S
=
αV T
C
P
, (4.142)
which is the equation for the adiabat, (3.32), that we derived in Chapter 3. We have now
rigorously demonstrated that this equation describes a process that is isentropic, hence the
partial derivative notation in (4.142). As we saw in Section 4.4, a transformation can be
adiabatic but not isentropic. In such a case the entropy of the system must increase during the
adiabatic transformation, and the relationship between P and T given by equation (4.142)
is no longer valid, because (4.140) is no longer valid. When we apply equation (3.32),
226 The Second Law of Thermodynamics
or (4.142), to calculate temperature in a convecting fluid (e.g. a planetary mantle) we are
assuming that the process is isentropic. Although this is commonly a good approximation,
it may not always be the case. In Chapter 3 we examined, and discarded, heat diffusion as a
possible source of entropy. We did not call heat diffusion an entropy-generating process, but
now we known that that is what it is. There may be other sources of entropy, however. Exam-
ples include dissipation of gravitational potential energy by separation of phases of different
densities, radioactive heating and viscous deformation. We return to this topic in Chapter 10.
4.9.2 The Gibbs free energy surface
Calculating and analyzing chemical equilibrium is in essence an exercise in computing and
comparing Gibbs free energy surfaces, and seeking the conditions under which different
surfaces intersect one another. We will perform these tasks algebraically rather than geo-
metrically (Chapter 5), but having a mental image of what the Gibbs free energy surfaces
look like is always a powerful aid in understanding what one is doing. The Gibbs free
energy of a system of constant composition at equilibrium varies as a function of pressure
and temperature as described by equations (4.132), (4.133) and (4.135)to(4.137). The
function G = G(P , T ) for a system at equilibrium is therefore always a surface with the
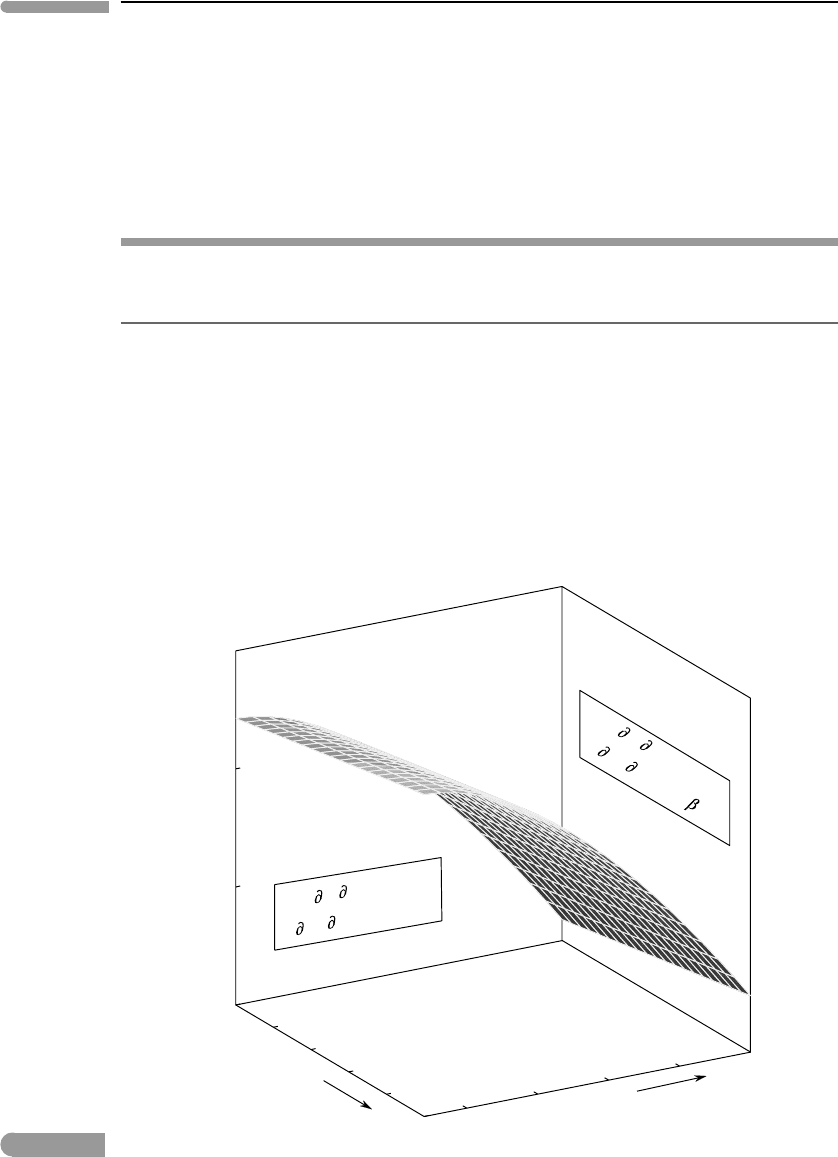
geometrical properties sketched in Fig. 4.13. The entropy of a system is always a positive
Temperature
Pressure
Gibbs free energy
(
G/
T)
P
=
–S
(
G/
P)
T
=
V
(
2
G/
P
2
)
T
=
–
V
T
(
2
G/
T
2
)
P
=
–C
P
/
T
Fig. 4.13
Geometry of the Gibbs free energy surface for any system at equilibrium. The slope and curvature of the G surface on
the T and P sections are given by the first and second derivatives of G, as shown in the figure, and always have the
same signs.

227 Exercises for Chapter 4
quantity. (Careful! Do not confuse this statement with the fact that the entropy change for
a process can be negative.) Therefore, the first temperature derivative of G is always neg-
ative, whereas the first pressure derivative (V ) is always positive, as shown in the figure.
The corresponding second derivatives are always negative (equations (4.135) and (4.136)),
so that the Gibbs free energy surface has negative curvature, as shown in Fig. 4.13. The
magnitudes of the slopes and curvatures may vary greatly, depending on the nature of the
system. For example, the curvature of the G surface relative to pressure at constant tem-
perature (equation (4.136)) is greater for gases than for solids and liquids, reflecting the
greater compressibility of gases. The first derivative relative to temperature at constant
pressure is also commonly greater for gases than for other substances, because gases have
higher entropy. The geometric properties of the G surface, however, are always as shown
in Fig. 4.13.
Exercises for Chapter 4
4.1 Show that isothermal expansion is accompanied by an increase in entropy.
4.2 Calculate the rate of entropy production by frictional heating during fault motion,
Section 1.12.3. This is an example of a process that is adiabatic but not isentropic.
Can you give other examples among planetary processes?
4.3 Formation of a mineral solid solution is accompanied by an increase in configurational
entropy, which as we shall see in Chapter 5 is an important aspect in the calculation
of equilibrium in natural systems. As a first example, derive a general expression
for the configurational entropy of orthopyroxene solid solution along the binary join
MgSiO
3
–FeSiO
3
, as a function of composition (i.e., X
Mg
or X
Fe
). What are the
configurational entropies of pure enstatite and of pure ferrosilite? What orthopyrox-
ene composition has maximum configurational entropy? How does configurational
entropy change with temperature?
4.4 Repeat Exercise 4.3 for olivine solid solution, between the end-members forsterite:
Mg
2
SiO
4
and fayalite: Fe
2
SiO
4
. How does you expression compare to the one for
orthopyroxene?
4.5 Consider a homogeneous mixture of two gases, 1 and 2, with mol fractions X
1
and
X
2
. Calculate the value of O for the mixed gas phase. Now consider the possibility
that there is a small inhomogeneity in the composition of the gas between different
parts of the container, such that the left hand side is richer in gas 1 and the right hand
side is richer in gas 2. Call this difference δ. Call the number of microstates of the
inhomogeneous gas mixture O
. Derive an equation for the ratio (O
/O) as a function
of δ and of the total number of molecules of gas, N . What is the meaning of the ratio
(O
/O)? What can you say about the magnitude of the largest random concentration
fluctuations that are likely to appear spontaneously in a homogeneous gas phase? How
does the magnitude of likely random concentration fluctuations relate to the size of
the system (i.e., the value of N )?
4.6 The following is known as Gibbs paradox. Consider three different experiments based
on the setup in Fig. 4.7. (i) Side A is filled with He at 1 bar and 298 K, assumed to
behave as an ideal gas, and side B is empty. The partition is removed and He expands
to fill the entire volume. Calculate the increase in entropy. (ii) Side B is filled with
