Douce A.P. Thermodynamics of the Earth and Planets
Подождите немного. Документ загружается.


228 The Second Law of Thermodynamics
He at 1 bar and 298 K, assumed to behave as an ideal gas, and side A is empty. The
partition is removed and He expands to fill the entire volume. Calculate the increase
in entropy. (iii) Both sides are filled with He at 1 bar and 298 K, assumed to behave as
an ideal gas. The partition is removed and the gases are allowed to mix. Does entropy
increase in this case? Why or why not? Resolve the paradox. The microscopic view
is essential.
4.7 Prove that the minimum energy principle leads to the condition of thermal equilibrium
(uniform temperature distribution) in a system evolving at constant entropy.
4.8 Modify the fundamental equation for Gibbs free energy, (4.129), to account for the
effect of mechanical work on Gibbs free energy. Derive equations for the rate of
change of Gibbs free energy of the Earth’s mantle during (i) the isobaric cooling
leg and (ii) the adiabatic decompression leg. Assume that the mantle is composed
of pure forsterite and ignore phase transitions of magnesium silicates. Estimate the
rate of change of Gibbs free energy of the mantle during the isobaric and adiabatic
legs. Thermodynamic properties can be found in Holland and Powell (1998) – use
values at 298 K and 1 bar. Assume that the mantle supports a shear stress of order
100 bar. Comment on the relative contributions of the various terms in the fundamental
equation to the rate of change of Gibbs free energy, and reconsider Exercise 4.3 in
the light of your results. Comment on the relative magnitudes and signs of the rate
of change of Gibbs free energy during adiabatic decompression and isobaric cooling,
and discuss how your results relate to the driving mechanism for mantle convection.
4.9 Find expressions for the heat capacities at constant volume and constant pressure,
the isothermal and adiabatic bulk moduli, the isobaric and adiabatic coefficients of
thermal expansion, and the Grüneisen parameter in terms of the second derivatives of
the thermodynamic potentials E, H , F and G.
4.10 Derive the relationships among all the mixed second derivatives of the thermodynamic
potentials E, H , F and G (Maxwell’s relations). Simplify these relationships as much
as possible using the expressions for material properties from Exercise 4.8.

5
Chemical equilibrium. Using composition as a
thermodynamic variable
A comprehensive understanding of planetary bodies requires that we study how changes
in physical conditions give rise to chemical phenomena. Physical conditions may be deter-
mined, for example, by the intensive variables P and T, where possible P–T combinations are
in turn determined by the nature of heat sources and heat transfer mechanisms (Chapters 2
and 3). Chemical phenomena are transformations that entail redistribution of matter among
and within phases. Some examples are: mineral transformations and melting in solid planets,
changes in the relative amounts of molecular species that make up a gas or a supercritical
fluid phase, and changes in the ionic constituents in an electrolyte solution such as seawater.
The study of phenomena such as these is based on a mathematical description of chemical
equilibrium, even in those cases in which departures from equilibrium cannot be ignored
(Chapter 12). In this chapter we lay the foundations for the study of chemical equilib-
rium, including a comprehensive discussion of the use of composition as a thermodynamic
variable. The principles and mathematical formalisms that we develop here are general,
but important differences in implementation for different types of systems exist. These are
dealt with in subsequent chapters.
5.1 Chemical equilibrium
5.1.1 Fundamental concepts
We begin by distinguishing between homogeneous and heterogenous systems. A homo-
geneous system consists of a single phase. Some examples are: gas in a container with
nothing else in it, a planetary atmosphere with no clouds nor suspended particulate matter,
or a mineral. A heterogeneous system is one in which we can identify more than one phase,
for example, the contents of a liquefied gas cylinder (liquid + gas), a planetary atmosphere
with clouds, or a polymineralic rock. The chemical composition of a system is specified by
the relative amounts of a minimum number of independently variable chemical components.
There are two requirements on this set of components, which are properly called system
components: (i) the components must be linearly independent, and (ii) they must span the
full compositional range of the system of interest. The system components may or may not
correspond to actual chemical species present in the system (e.g. molecules, ions, etc.). For
example, the composition of a homogeneous gas phase that contains the chemical species
H
2
O, H
2
,CO
2
, CO, CH
4
and NH
3
can be described in terms of the relative amounts of the
four system components C, H, O and N. We shall define these concepts more rigorously in
Chapter 6, but for now this intuitive introduction will suffice.
The state of chemical equilibrium in a system at constant pressure and temperature is
the one in which the Gibbs free energy of the system takes its minimum possible value.
229

230 Chemical equilibrium
0 50 100 150 200
–3*10
5
–2*10
5
–10
5
0
–3*10
5
–2*10
5
–10
5
0
T(°C)
H
2
O gas
H
2
+ 1/2 O
2
r
G
P, T, n
i
<0
0 50 100 150 20
0
G(J mol
–1
)
G(J mol
–1
)
H
2
+ 1/2 O
2
H
2
O gas
H
2
O liquid
(a)
P = 1 bar P = 1 bar
(b)
Fig. 5.1
Isobaric sections across the Gibbs free energy surfaces for a 2:1 mixture of molecular hydrogen and oxygen, H
2
O gas
and H
2
O liquid. The equilibrium state at any P and T is the one for which G takes its minimum value.
Consider a homogeneous system consisting of a gas composed of hydrogen and oxygen in
an atomic ratio2H:1O.There are at least two possible states for this homogeneous system:
a mixture of molecular H
2
and O
2
in a ratio of 2:1 or gaseous H
2
O (other possibilities that
we are not considering would be mixtures of atomic and/or ionic species). Which of the two
is the equilibrium state? If we specify the temperature and pressure for which we seek an
answer, then all we need to do is calculate the Gibbs free energy of each of the two possible
states of the system, and determine which of the two is the smallest value.
Figure 5.1a shows Gibbs free energy for a 2:1 hydrogen–oxygen mixture, and for H
2
O gas,
as a function of temperature and at a constant pressure of 1 bar. The theoretical framework
for these calculations is discussed in Box 5.1, and a calculation procedure using Maple is
explained in Software Box 5.1. The figure shows that the Gibbs free energy of gaseous
H
2
O is everywhere lower, within this temperature range, than that of a physical mixture
of hydrogen and oxygen with the same chemical composition. What this means is that the
spontaneous process at constant temperature and pressure, i.e. the one that will minimize
the thermodynamic potential G, is the combination of hydrogen and oxygen to form H
2
O.
The difference in Gibbs free energy that accompanies the chemical reaction is called the
Gibbs free energy of reaction,
r
G (see Fig. 5.1a). For a spontaneous chemical reaction,
it must be
r
G<0. Thus, H
2
O does not spontaneously break up into H
2
+O
2
at these
conditions because
r
G for that process is greater than zero. Water can break up into
hydrogen and oxygen at room temperature, for example by electrolysis, but in that case
electrical work is being performed on the system so the process is not “spontaneous”.
Box 5.1
Calculation of Gibbs free energy
We seek an explicit expression for the Gibbs free energy of a chemical species at any arbitrary temperature
andpressure.For now let us define a species as an entity(compound,pureelementorion)whosecomposition
in the system of interest remains fixed. For example, O
2
and H
2
O are two of the chemical species in the
terrestrial atmosphere, H
2
O and Na
+
are two of the chemical species in seawater, and forsterite and fayalite
are chemical species in olivine.

231 5.1 Chemical equilibrium
Box 5.1
Continued
In this book I symbolize the standard state molar Gibbs free energy of a chemical species at P and T
by G
0
P,T
. Symbols for thermodynamic variables in all chemical equilibrium equations will be in uppercase
non-bold font, representing molar quantities (Section 1.9). The superscript
0
means “standard state” and
indicates that the value of G corresponds to the pure chemical species at those conditions. We will see that
this is different from G of the chemical species in a solution. For example, the standard state molar Gibbs free
energy of oxygen at 1 bar and 20
◦
C, symbolized by G
0
1,298
, is the molar Gibbs free energy of pure oxygen at
those conditions, but it is not equal to the Gibbs free energy of oxygen in air at 1 bar and 20
◦
C. Similarly, G
0
of forsterite is not the same as the Gibbs free energy of forsterite in an olivine solid solution at the same P
and T.
The reference statefor Gibbs freeenergy is 298.15K and 1 bar, and we symbolize G
0
at these conditionsby
G
0
1,298
. This notation is not standard, but in my experience it is the clearest one, because it states explicitly the
conditions at which one is evaluating the thermodynamic function. Using (4.132) and (4.133), and recalling
that S and V are functions of temperature and pressure, we see that the Gibbs free energy for the chemical
species at any other P and T is given by:
G
0
P,T
=G
0
1,298
−
T
298
S(P, T) dT +
P
1
V(P,T) dP. (5.1.1)
We need to find explicit expressions for the three terms in the right hand side of equation (5.1.1). The two
integrals can be evaluated in any order, but the simplest, and standard, way is the following: evaluate the
temperature integral along an isobaric path at 1 bar, from 298 K to T, and evaluate the pressure integral
along an isothermal path at T, from 1 bar to P. Alternative ways of doing this, which lead to the same result,
are proposed in end-of-chapter problems.
(i) Gibbs free energy at the reference state. The value of G
0
1,298
is listed in some thermodynamic data bases as
the reference state Gibbs free energy of formation,
f
G
0
1,298
. This is defined as the Gibbs free energy of
a chemical species measured relative to G of its constituent elements, which are arbitrarily set to zero for
all pure elements in their stable configurations at 298.15 K and 1 bar. This is the same as the definition of
enthalpy of formation (Section 1.13.1), but recall that the entropy of pure elements at these conditions is not
zero (Section 4.7.2). Thus, whereas
f
H
0
1,298
is a measured quantity (heat evolved at constant pressure),
f
G
0
1,298
is not. It includes a contribution from the difference between the entropy of the compound and
the (non-zero) entropies of the elements at 298 K. The reference state Gibbs free energy of formation is
commonly (but not always!) defined as follows:
f
G
0
1,298
=
f
H
0
1,298
−298
S
0
298
, (5.1.2)
where (S
0
298
) is the difference between the Third Law entropy of the species of interest and those of
its constituent elements in their stable configuration, taken at 298.15 K and 1 bar (equation (4.70)). All
thermodynamic data bases list values of
f
H
0
1,298
and S
0
298
, so that it is always possible to calculate
f
G
0
1,298
(which is the value of G
0
1,298
in equation (5.1.1)) with (5.1.2), if its value is not listed. We will see, however,
that although the value of G
0
1,298
is needed in order to calculate the Gibbs free energy of a chemical species,
it is not required when calculating the change in G associated with chemical reactions, called the Gibbs free
energy of reaction,
r
G.

232 Chemical equilibrium
Box 5.1
Continued
(ii) The temperature integral. We expand the temperature integral in equation (5.1.1) by using (4.135), as
follows:
T
298
S(1,T)dT =
T
298
S
0
298
+
T
298
C
P
T
dT
dT
=S
0
298
(
T −298
)
+
T
298
T
298
C
P
T
dT dT, (5.1.3)
where S
0
298
is the Third Law entropy of the chemical species at 298 K (not the “entropy of formation”, see
Section 4.7.2). The double integral is easily solved by parts. Defining:
u =
T
298
C
P
T
dT
v = T
(5.1.4)
we get:
T
T
298
C
P
T
dT =
T
298
T
298
C
P
T
dT dT +
T
298
C
P
dT. (5.1.5)
Rearranging and substituting in (5.1.3):
T
298
S(1,T)dT = S
0
298
(
T −298
)
+T
T
298
C
P
T
dT −
T
298
C
P
dT. (5.1.6)
In order to evaluate the heat capacity integrals one must substitute the appropriate heat capacity
equations, see Software Box 1.1. These equations are polynomials in T that are empirical fits to measured
C
P
values and may not have a strong physical foundation, beyond being able to reproduce the weak
temperature dependence of heat capacity above the Debye temperature (Section 1.14.3 and Chapter 8).
The choice of C
p
(T) equation is generally dictated by the choice of data base. Throughout most of this
book we use thermodynamic data from Hollandand Powell (1998), who rely on the Shomate heat capacity
equation. An important exception is the calculation of phase equilibria at very high pressures, for which a
different heat capacity equation will be used (Chapter 8).
It is useful to start collecting terms incrementally, as we find expressions for each of the components of
equation (5.1.1). Using (5.1.6) we can write an expression for the Gibbs free energy of a chemical species
at T and P as follows:
G
0
P,T
=
f
G
0
1,298
−S
0
298
(
T −298
)
−T
T
298
C
P
T
dT +
T
298
C
P
dT +
P
1
V(P,T)dP. (5.1.7)
(iii) The pressure integral. Evaluation of the pressure integral requires that we substitute an explicit equation of
state for the material, which is a function V = V(P, T). As we discussed in Chapter 1, condensed phases
(solids and liquids) and non-condensed phases (gases) respond very differently to changes in pressure.
Their equations of state are different enough that we need to consider each case separately.
(iii)(a) Condensed phases. The simplest approximation for condensed phases is to assume that their volume
does not change with pressure or temperature. The pressure integral in equation (5.1.7) is evaluated

233 5.1 Chemical equilibrium
Box 5.1
Continued
at constant temperature T . Let V
1,T
be the volume of the chemical species at 1 bar and T. If V is
constant, then the pressure integral is simply:
P
1
V(P,T)dP =V
1,T
P
1
dP =
(
P −1
)
V
1,T
≈PV
1,T
, (5.1.8)
where for pressures of more than a few tens of bars we can assume that the lower limit
of integration vanishes. Note that equation (5.1.8) is written in terms of the volume at the
temperature of interest, T , but molar volumes of chemical species are typically tabulated at a
reference temperature of 298 K. Thermal expansion is not insignificant, but, again, we can ignore
it as a first approximation and calculate (5.1.8) by using the reference state volume, V
1,298
.
These approximations (incompressible phases that undergo no thermal expansion) are generally
acceptable for near-surface conditions, but accurate calculation of Gibbs free energy requires that
we account for changes in molar volume with pressure and temperature, as well as for the
temperature dependence of the coefficient of thermal expansion and the temperature and pressure
dependencies of the bulk modulus. We discuss this in Chapter 8.
(iii)(b) Gases. The simplest treatment for gases results from assuming ideal gas behavior. Using the ideal gas EOS,
the pressure integral is simply:
P
1
V(P,T)dP = RT
P
1
dP
P
=RT lnP. (5.1.9)
Real gases approach ideal gas behavior if their temperature is much higher than the critical
temperature, and at very low pressure (Chapter 9). Equation (5.1.9) is applicable to surface
environments in the terrestrial planets (except perhaps Venus). Equations of state for fluids
in planetary interiors are discussed in Chapter 9.
Summary
We summarize our results so far. For pressure and temperature conditions characteristic of the surface
and shallow crust of the large terrestrial planets (and perhaps much of the interior of small solid bodies),
the Gibbs free energy of a species in a condensed phase can be approximated to first order by combining
equations (5.1.7) and (5.1.8):
G
0
P,T
=
f
G
0
1,298
−S
0
298
(
T −298
)
−T
T
298
C
P
T
dT +
T
298
C
P
dT +PV
1,298
. (5.1.10)
For gases at P–T conditions that are far removed from their critical point (low pressure, high temperature)
the pressure term is replaced with (5.1.9), and we obtain:
G
0
P,T
=
f
G
0
1,298
−S
0
298
(
T −298
)
−T
T
298
C
P
T
dT +
T
298
C
P
dT +RT ln P. (5.1.11)

234 Chemical equilibrium
Software Box 5.1 Calculation of Gibbs free energy of ideal gas and incompressible phase
The file th_template_2.mw contains the following two new Maple procedures:
Gsurf_idealgas: calculates the Gibbs free energy of an ideal gas, or of a mixture
of ideal gases, with equation (5.1.11). Thermodynamic properties are entered in
the spreadsheet RefStateData, and the gas or mixture of gases are specified in
a table with two columns, as explained in Software Box 1.1. The procedure calls
on procedures in the package th_shomate.mw to perform the heat capacity
integrals, and then adds the pressure integral. It performs the calculations over
a P –T range and with P –T increments that are specified in the procedure call.
Output is sent to a text file whose name is specified in the procedure call.
Gsurf_Vconst: works as Gsurf_idealgas but assumes that the volume of the
phase or assemblage is constant (pressure integral as in equation (5.1.10)).
The data for hydrogen, oxygen and water are stored in tab-delimited format in a file
named waterprops.
There is, of course, more to this story. In the first place, we know that if the temper-
ature is lower than 100
◦
C at 1 bar, then the equilibrium condition is not H
2
O gas but
liquid H
2
O. The reason why this does not show up in Fig. 5.1a is that I have not included
the curve that represents the Gibbs free energy function for liquid H
2
O. This situation is
rectified in panel (b) of the figure. We can now compare Gibbs free energies for three
different possible states of a system with the same chemical composition. At any given
pressure and temperature, the equilibrium state, which we also call the stable state,is
the one in which Gibbs free energy is lowest. At 1 bar pressure molecular H
2
O is sta-
ble relative to H
2
+O
2
everywhere in the temperature interval 0–200
◦
C. At T<100
◦
C
the Gibbs free energy of liquid water is lower than that of H
2
O gas, so that the stable
state is liquid water. The converse is true at T>100
◦
C. At T = 100
◦
C and P = 1 bar
the Gibbs free energies of liquid and gaseous H
2
O are the same, so that both phases
are stable.
There is another aspect that we must consider. If we mix hydrogen and oxygen in a
container at room temperature we know from Fig. 5.1a that the system is not at equilibrium
and that a spontaneous reaction that lowers the system’s Gibbs free energy by forming
molecular H
2
O should take place. But does this happen? Hydrogen-filled airships were
built and flown in Germany for many years with no apparent inconveniences, until the
Hindenburg disaster in 1937. The answer is that in order for the reaction to take place we
need to “excite” the system, for example, by supplying heat in the form of an open flame or
an electrical spark (which is what apparently doomed the Hindenburg). The effect of this
excitation is to break the bonds in the H
2
and O
2
molecules, so that the atoms are able to
recombine as H
2
O molecules. This is the chemical equivalent of removing a restriction in a
system, such as a wall separating two different gases or an insulating layer between bodies
at different temperatures. We saw that, when such restrictions are removed, isolated systems
evolve spontaneously in the direction mandated by the Second Law of Thermodynamics.
In the case of a chemical reaction the restrictions are the chemical bonds in the molecules of
the reactant species. We remove that restriction by supplying the amount of energy required
to break those bonds. This energy is called the activation energy for the chemical reaction,
which we will discuss in Chapter 12.

235 5.1 Chemical equilibrium
5.1.2 Gibbs free energy surfaces and phase boundaries
The curves in Fig. 5.1 are isobaric sections across Gibbs free energy surfaces such as that
in Fig. 4.13. We can represent Gibbs free energy surfaces by means of contour lines of
constant G projected on a P –T plane, as shown in Fig. 5.2. The solid curves are contours
on the G surface for H
2
O gas, and the dotted lines are contours on the G surface for liquid
H
2
O. The different shapes of the two sets of curves reflect the different effects of pressure
on the Gibbs free energy of condensed and non-condensed phases, as discussed in Box 5.1
and in more detail in Chapters 8 and 9. The Gibbs free energy of a gas is a strong function of
pressure, whereas G of a liquid or solid is much less sensitive to pressure. Within the P –T
range of the figure, and for the contour interval chosen (2 kJ), there are four intersections
between contour lines, marked with the solid circles. These are four points on the intersection
between the two surfaces, which is shown by the thick solid curve. Along this curve the
Gibbs free energy of the liquid and of the gas are the same, so that the two phases are in
heterogeneous chemical equilibrium. The curve is a phase boundary. We can see that the
thermodynamic condition for a phase boundary is simply:
r
G
P ,T ,n
i
=0, (5.1)
40 60 80 100 120 140
0
1
2
3
4
T(°C)
P (bar)
–242
–24
0
Liquid
Gas
–240 –244
–246
–24
2
–24
4
–24
6
–24
8
–25
0
–230
Fig. 5.2
Phase diagram for H
2
O. Data from Robie et al. (1995) were used to calculate the Gibbs free energy surfaces for liquid
and gaseous H
2
O as explained in Software Box 5.1, assuming ideal gas behavior for H
2
O gas. Solid curves are contours
on the G surface for gas, dashed lines are contours on the G surface for liquid. Numbers on the right and top side of the
diagram are Gibbs free energies in kJ mol
−1
. Intersection between the two surfaces yields the phase boundary
(
r
G =0), shown by the thick curve. Four intersection points between the contour lines are shown with big dots.
236 Chemical equilibrium
where the Gibbs free energy of reaction,
r
G is defined in the same way as
r
H
(equation (1.86)). A phase boundary is the locus of points for which
r
G =0.
The diagram in Fig. 5.2 is an example of a phase diagram. It shows which is the stable
phase for different combinations of intensive variables. For each combination of pressure
and temperature that is not on the phase boundary there is one phase that has lower Gibbs
free energy. Equilibrium requires that the phase with lower Gibbs free energy, called the
stable phase, forms at the expense of the other one. In this example, two phases (liquid and
gaseous H
2
O) are stable (i.e. they are at equilibrium) along the phase boundary. On the high
pressure - low temperature side of the phase boundary, shown in dark grey, G
liquid
<G
gas
,
so the stable phase is liquid H
2
O. On the other side of the phase boundary, shown in light
grey, we have G
gas
<G
liquid
, so the stable phase is H
2
O gas. Note that these relations refer
to molar Gibbs free energy, i.e. an intensive property.
Phase diagrams can become more complex in systems composed of more chemical
species than this one, and phase diagrams can be constructed so as to show phase equilibrium
as a function of other intensive variables besides pressure and temperature. In every case,
however, it is of great help to keep in mind that a phase diagram is simply a set of curves
defined by intersections among Gibbs free energy surfaces.
5.1.3 Properties of phase boundaries and phase transitions
We can make some useful generalizations about phase equilibrium by examining the geom-
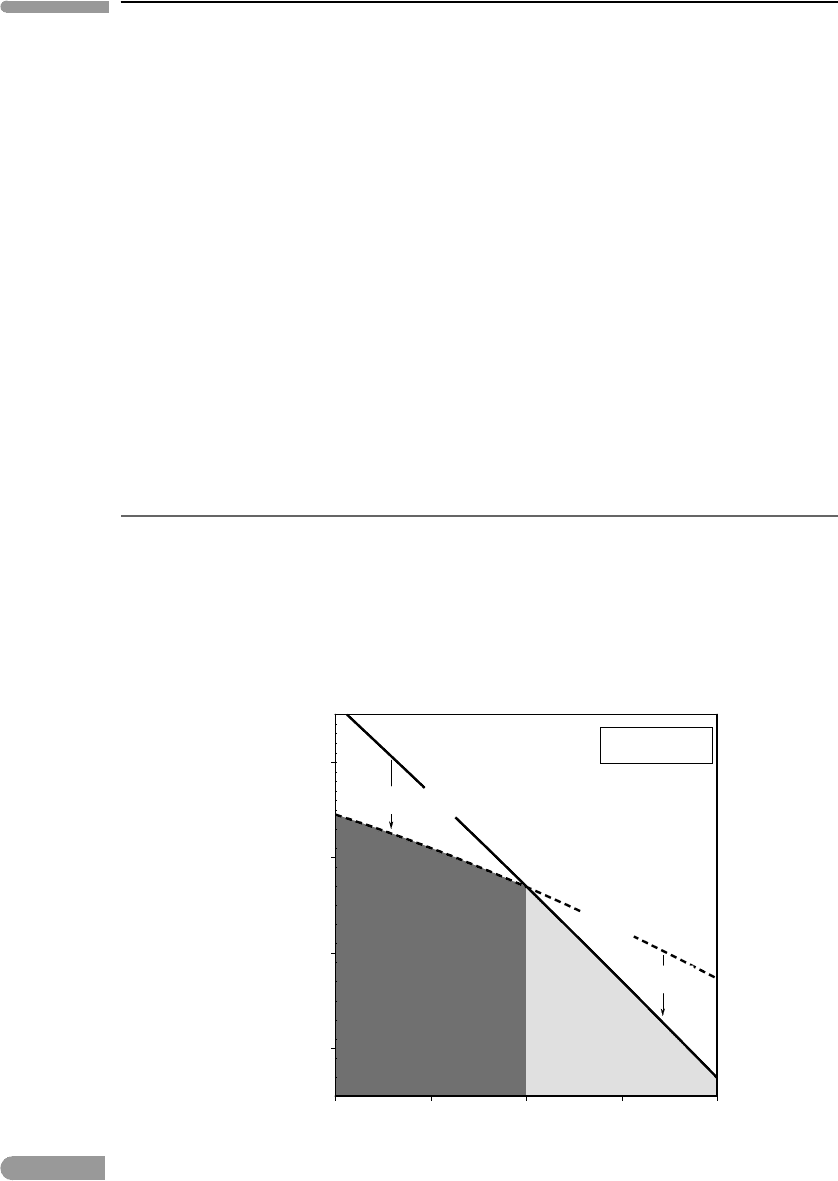
etry of the G surfaces in Fig 5.2 along an isobaric cross section (e.g. at P =1 bar, Fig. 5.3)
and an isothermal cross section (e.g. at T =100
◦
C, Fig. 5.4). The intersections of the curves
in these two diagrams represent one and the same point on the phase boundary in Fig. 5.2:
equilibrium between liquid and gaseous H
2
O at 1 bar and 100
◦
C. This example deals with
a phase boundary that separates two distinct phases with the same chemical composition. A
0 50 100 150 20
0
–2.6*10
5
–2.5*10
5
–2.4*10
5
–2.3*10
5
T(°C)
G (J mol
–1
)
Liquid Gas
Liquid
Gas
H
2
Oat1bar
G<
∆
0
G<0
∆
Fig. 5.3
Isobaric section across the phase diagram for H
2
O. The phase that is stable on the high-temperature side of the phase
transition must have a steeper G–T curve, so its entropy must be higher than that of the low-temperature phase.
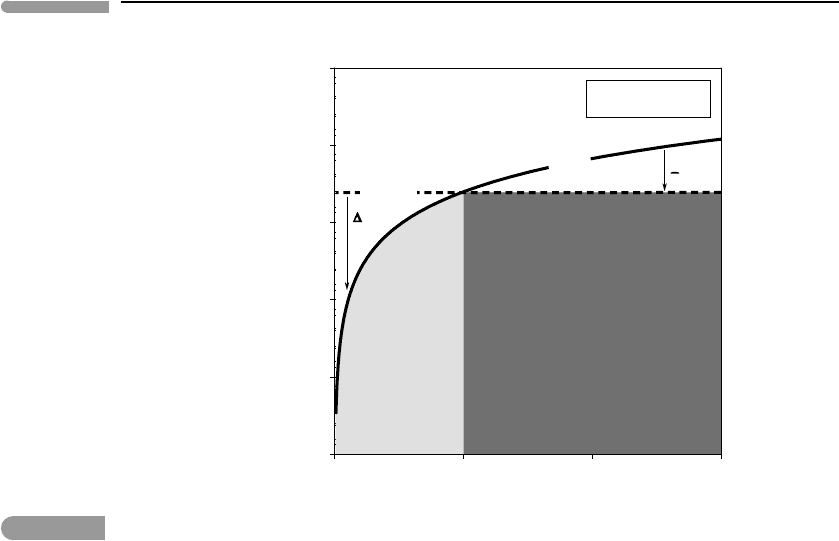
237 5.1 Chemical equilibrium
012
3
–2.6*10
5
–2.55*10
5
–2.5*10
5
–2.45*10
5
–2.4*10
5
–2.35*10
5
P (bar)
G (J mol
–1
)
LiquidGas
Liquid
Gas
H
2
Oat100
o
C
∆G<0
G<0
Fig. 5.4
Isothermal section across the phase diagram for H
2
O. The phase that is stable on the low-pressure side of the phase
transition must have a steeper G–P curve, so its molar volume must be higher (its density lower) than that of the
high-pressure phase. The stronger curvature of the G surface for the gas reflects the higher compressibility of gases
relative to condensed phases.
phase boundary in a one-component system is called a discontinuous, or first-order, phase
transition. The Gibbs free energy is continuous at a discontinuous phase transition, as it
must be given that this is the definition of equilibrium between the two phases. The first
derivatives of G (S and V ) are, however, discontinuous at the phase transition (this is where
the name comes from). This also implies that there is a finite enthalpy change associated
with first-order phase transitions (see Worked Example 1.1). Moreover, if the first deriva-
tives of G are discontinuous, then the second derivatives, heat capacity and compressibility
(equations (4.135) and (4.136)), are undefined at the phase transition. This means that as
long as the two phases coexist at equilibrium the system water–steam can absorb indefinite
amounts of thermal and mechanical energy without its temperature or pressure changing,
although the relative amounts of the two phases will change.
The isobaric section (Fig. 5.3) shows that the slope of the G surface for H
2
O gas is steeper
than that for liquid H
2
O. By equation (4.132), the interpretation of this is that the entropy
of the gas is higher than the entropy of the liquid. This conclusion is general and expected
on physical grounds. The entropy of a non-condensed phase must be higher than that of a
condensed phase with the same chemical composition because transition from a condensed
to a non-condensed state (boiling or sublimation) requires absorption of thermal energy
in order to break intermolecular bonds, and heat absorption means an increase in entropy
(equation (4.6)). The microscopic interpretation is that there is an increase in the number
of accessible microstates for molecular vibrations.
From the geometry of the isobaric section it follows that, among condensed phases, the
entropy of the solid must be lower than the entropy of the liquid, because the intersection
that defines the melting point must occur at lower temperature than the one that defines the
