Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

248 Chemical equilibrium

potential of the species KAlSi

must be the same in the crystal as in the melt, and in

order for water ice to be stable on the Martian surface the chemical potential of H

O must

be the same in surface ice as in the Martian atmosphere. This seemingly trivial corollary of

(5.22) is a fundamental concept that we will rely on many times.

Suppose now that the system composed of the two phases A and B is not at equilibrium.

Then a spontaneous transfer of component σ between the phases at constant temperature

and pressure, say from A to B, can take place only if it leads to a decrease in the Gibbs free

energy of the system. Expanding (5.21) we have:

dG =



−µ



< 0. (5.25)

But if matter is transferred from A to B then it must be dn

< 0, which implies that:

>µ

. (5.26)

In other words, chemical species are transferred down chemical potential gradients. This is

what we should have expected given that µ and n are conjugate variables (Section 4.8.4) and

also justifies the name chemical potential for the thermodynamic variable µ. Equilibrium

is reached once mass transfer among phases eliminates chemical potential gradients. The

proof that equation (5.26) generalizes to systems with any number of phases and chemical

species is left as an exercise.

5.4 Partial molar properties

Finding the function that relates the chemical potential of a phase component to its standard

state Gibbs free energy and to the composition of the solution requires several steps. We

begin by noting that we can express any extensive thermodynamic property of a solution,

sol

, as a sum of products of intensive quantities z

for each of the i components of the

solution, times the amount (an extensive quantity, for example the number of mols, n

)of

each component, as follows:

sol



. (5.27)

We make no claims as to the functional form of the z

s, and in particular, as to whether

or not the various z

s are a function of each other. Equation (5.27) is simply an algebraic

identity. We do require, however, that the amount of each component, n

, be independently

variable, so these must be phase components (for example, we can add forsterite to olivine

without changing the amount of fayalite). Z

sol

being a thermodynamic variable, it is also

a function of temperature and pressure. It then follows from (5.27) that the quantities z

called partial molar quantities, are defined by the following derivative:

≡



∂Z

sol

∂n



P ,T ,n

j≡i

. (5.28)

It is important to understand what this equation means: partial molar z of component i,an

intensive variable symbolized z

, equals the rate of change of Z of the solution (an extensive

variable) relative to a change in the amount of component i (also extensive), while keeping

249 5.4 Partial molar properties

pressure, temperature and the amounts of all other components constant. Dividing (5.27)by

the total number of mols in the system we obtain molar Z of the solution, Z

sol

, as follows:

sol





, (5.29)

where X

is the mol fraction of component i.

Obviously, the thermodynamic property Z also takes a definite value for each of the

solution components when they are in their standard states. For a component i we symbolize

this by Z

0,i

, reserving the subscript slot to state the pressure and temperature of the standard

state, if needed (e.g. Section 1.13.1). On dimensional grounds it is evident that z

and Z

0,i

refer to the same type of thermodynamic property (e.g. they must both have dimensions of

volume per mol, energy per mol or entropy per mol). Note, however, a very important point:

we have made no assumptions about the relationship between z

and Z

0,i

. In particular,

the definitions of the two variables are not the same. Whereas the standard state property,

0,i

, is defined independently of the properties of a solution (for example, for a pure

chemical species), the definition of the corresponding partial molar property z

is based on

the behavior of a particular solution that contains i. There is no expectation that the two

variables take on the same value, so that we can write the following equation:

sol



0,i

+Z

mixing

. (5.30)

We take (5.30) as the definition of Z

mixing

, noting that this quantity is defined for the

solution (not for the components). For a pure chemical species (equivalently, a phase of

fixed composition), there is only one component, for which X

= 1, so that in this case z

is always equal to Z

0,i

, for any thermodynamic variable, and Z

mixing

is obviously zero.

There is an additional relationship among partial molar properties and the molar prop-

erty of the solution that plays a central role in the study of solutions. For a solution of

k components, the partial molar property of the ith components is given by:

sol

j=k



j=2



−X



∂Z

sol

∂X

, (5.31)

where the symbol δ

, called the Kronecker delta, takes the value 1 if i =j , and 0 otherwise.

The proof and geometric interpretation of (5.31) are given in Box 5.2.

Box 5.2

Proof of equation 5.31

Let Z be any extensive thermodynamic variable. We can write Z for a solution of k components as a function

of the form:

sol

(

P, T, n

, ...,n

)

(5.2.1)

or, equivalently, as a function of the total number of mols, n =



and the mol fractions of any k −1

components (the kth is not linearly independent):

sol

(

P,T,n,X

, ...,X

)

. (5.2.2)

250 Chemical equilibrium

Box 5.2

Continued

This is a simple change of coordinates: note that the functions (5.2.1) and (5.2.2) have the same number of

variables, and that, as long as we know n, it is always possible to convert the n

stoX

s and vice versa. Molar

Z of the solution, Z

sol

, is obtained by dividing (5.2.2)byn, and, because n is the only extensive independent

variable in (5.2.2), this results in:

sol

(

P, T, n, X

, ...,X

)

sol

(

P, T,1,X

, ...,X

)

. (5.2.3)

We now use (5.2.3) to re-write the deﬁnition of the partial molar property z

(equation (5.28)) as follows:



∂



sol



∂n



P,T,n

j≡i

sol



∂n



P,T,n

j≡i



∂Z

sol

∂n



P,T,n

j≡i

. (5.2.4)

Because all n

j=i

are kept constant, it is:



∂n



P,T,n

j≡i

=1. (5.2.5)

Using (5.2.3) we write the partial derivative in the second term of the right-hand side of (5.2.4) as follows:



∂Z

sol

∂n



P,T,n

j≡i

j=k



j=2



∂Z

sol

∂X

∂n



P,T,n

j≡i

(5.2.6)

and, using (5.2.5):



∂X

∂n



P,T,n

j≡i



∂X

∂n



P,T,n

j≡i



∂X

∂n



P,T,n

j≡i



∂X

∂n



P,T

. (5.2.7)

In the last identity we have dropped the constraint n

j=i

because we are now differentiating relative to the

total number of mols. Each mol fraction is given by:

(5.2.8)

so:



∂X

∂n



P,T

∂

∂n





P,T



∂n

−X



P,T

. (5.2.9)

Component i can be any arbitrary component, either component 1 or any one of the k −1 components

between j = 2 and j = k. We need to account for all possibilities. For n

j=i

it is ∂n

/∂n = 0, whereas for

j=i

we have ∂n

/∂n =1. We can then write (5.2.9) using the Kronecker delta: δ

=1ifi = j, δ

=0if

i = j, as follows:



∂X

∂n



P,T



−X



. (5.2.10)

251 5.4 Partial molar properties

Box 5.2

Continued

Substituting into (5.2.6):



∂Z

sol

∂n



P,T,n

j≡i

j=k



j=2



−X



∂Z

sol

∂X

. (5.2.11)

Substituting (5.2.11)in(5.2.4) and using (5.2.5):

sol

j=k



j=2



−X



∂Z

sol

∂X

, (5.2.12)

which is (5.31).

This equation comes up repeatedly in the study of solutions, and it is helpful to visualize its geometry.

This is best done by considering a system of two components, a and b, in which case (5.2.12) becomes:

sol

−X

∂Z

sol

∂X

. (5.2.13)

Rearranging as follows:

∂Z

sol

∂X

sol

−z

(5.2.14)

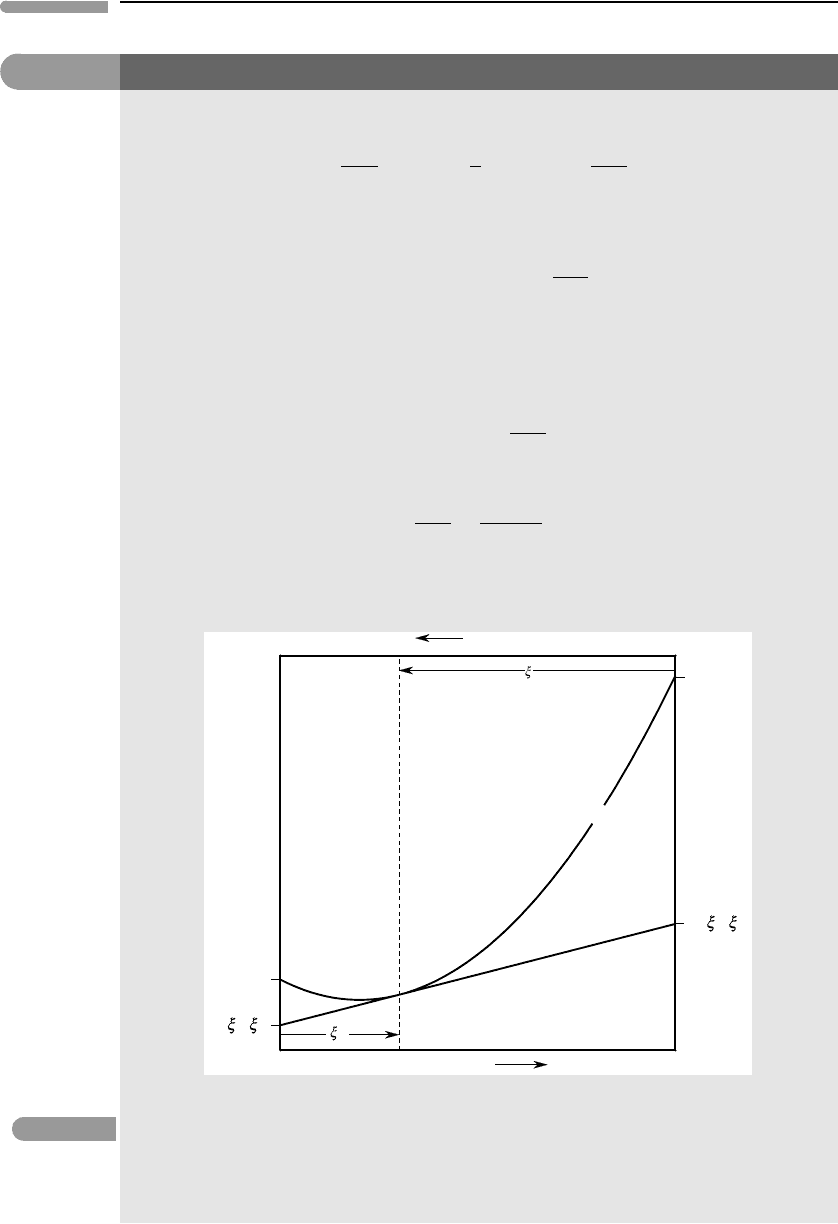
it is easy to see (Fig. 5.7) that the partial molar properties z

and z

for a given solution composition, say at

mole fractions ξ

, and ξ

=1 −ξ

, are the intercepts of the tangent line to Z

sol

at that composition with

0, b

sol

(

)

0, a

(

)

Fig. 5.7 Geometric interpretation of the relationships between the molar property of a solution, Z

sol

, standard state molar

properties of end-member species, Z

0,a

and Z

0,b

, and partial molar properties of the species in solution, z

and z

Partial molar properties, shown in the ﬁgure for a speciﬁc solution composition given by ξ

and ξ

=1 −ξ

, are

functions of composition.

252 Chemical equilibrium

Box 5.2

Continued

the Z axis at X

= 1 and X

= 1, respectively. This is true for any extensive thermodynamic function that

can be written as (5.27), and regardless of the functional form of Z

sol

. The geometric point of view (Fig. 5.7)

is particularly helpful in emphasizing that, whereas Z

0,i

is a constant at a given P and T , z

varies with the

composition of the solution at constant P and T (except for a property for which Z

sol

is a linear function).

The geometry is the same for multicomponent solutions, except that the tangent line is replaced by a

tangent n −1 plane embedded in an n-dimensional space, where n is the number of components in the

solution.

Equations (5.27) through (5.31) are algebraic identities that can be applied to any exten-

sive thermodynamic state variable, for instance, enthalpy, entropy, volume and Gibbs free

energy. With one exception, the partial molar property is symbolized with the same let-

ter used for the standard state molar property but written in lowercase (e.g. partial molar

entropy, s) rather than uppercase (e.g. standard state molar entropy, S

). The exception

is Gibbs free energy. Comparison of (5.28) with (4.134) shows that the partial molar

Gibbs free energy is the chemical potential, µ. It is customary to symbolize the standard

state molar Gibbs free energy of a pure species by µ

, and to call it the standard state

chemical potential. This is physically appealing given that the interpretation of chemical

potential as a driving force for transfer of matter (equation (5.26)) is also true for pure

chemical species. In this book we will use both µ

0,i

and G

0,i

, depending on the context,

but you must keep in mind that the identity µ

0,i

= G

0,i

is always true. Summarizing,

we have:

sol



0,i

+G

mixing

(5.32)

sol



0,i

+S

mixing

(5.33)

sol



0,i

+H

mixing

(5.34)

sol



0,i

+V

mixing

. (5.35)

The pressure and temperature derivatives of chemical potential follow the same rules as

those of Gibbs free energy. Thus (omitting the constant variable subscripts for clarity, see

Box 1.3):

∂µ

∂P

∂

∂P



∂G

sol

∂n



∂

∂n



∂G

sol

∂P



∂V

sol

∂n

(5.36)

or:



∂µ

∂P



. (5.37)

253 5.5 Generalized equilibrium condition

And by an identical procedure:



∂µ

∂T



=−s

. (5.38)

5.5 Generalized equilibrium condition. Activity and the

equilibrium constant

5.5.1 Definition of activity

We now have the background needed to derive the algebraic expression that describes

equilibrium among chemical species in any state, as a function of temperature, pressure,

composition and thermodynamic properties in the standard state. We begin by defining a

new thermodynamic variable called activity. Using equation (4.128) (last line) we write the

following equation for the molar properties of a solution:

sol

−TS

sol

. (5.39)

We can re-write this in terms of partial molar properties, by using (5.32), (5.33) and (5.34):



−T



(5.40)

from which, given that the mol fractions can vary independently, we derive an identity valid

for each component i:

−Ts

. (5.41)

Equation (4.128) also yields the following relationship between standard state molar

properties:

0,i

−TS

0,i

. (5.42)

Subtracting (5.42) from (5.41) and rearranging:

=µ

0,i



−H

0,i



−T



−S

0,i



. (5.43)

The terms in this equation have dimension of energy. We can therefore choose to write the

sum of the last two terms on the right-hand side as the product of the gas constant, R, times

temperature, T, times a non-dimensional variable. We define this non-dimensional variable,

called activity and symbolized by a, as follows:

ln a

≡



−H

0,i



−



−S

0,i



(5.44)

from which we get:

=µ

0,i

+RT ln a

. (5.45)

254 Chemical equilibrium

There are different ways of defining activity (see, for example, Guggenheim, 1967).

Equation (5.44) is not orthodox, but it is elegant. All definitions converge on equation

(5.45). It is very important to understand what this equation is saying. Activity is a non-

dimensional parameter that measures the chemical potential of a component in a solution

relative to the chemical potential of the same chemical species in a specified standard state.

Activity is a relative quantity that has meaning only if the standard state that it refers to is

given explicitly. This standard state could be, for example, the pure chemical species in the

same physical state as the solution (e.g. solid in a certain crystalline state, liquid, gas) and at

the pressure and temperature of interest. We could also specify a different standard state, and

if we do so then, as is readily apparent from (5.45), the value of the activity must also change,

because it now measures the same chemical potential relative to a different reference level.

Worked Example 5.2 Activity of components in silicate melts: an example of changing the

standard state

Consider a silicate melt saturated in quartz, for instance, a granitic melt. By “saturated” we

mean that crystalline quartz is at equilibrium with the melt, so that we have:

0,SiO

quartz

=µ

SiO

quartz

=µ

SiO

melt

(5.46)

The identity µ

0,SiO

quartz

=µ

SiO

quartz

comes from (5.30), noting that for pure quartz it is X

SiO

=1.

We wish to specify the activity of SiO

in the melt, but in order to do so we must first define

the standard state relative to which the activity is to be measured. One possibility is to define

the standard state as pure crystalline quartz at the pressure and temperature of interest. As

with chemical potential, it is convenient to label activity with the identities of the chemical

species and the phase, thus: a

. If we call the activity of SiO

in the melt relative to a

standard state of pure crystalline quartz at the pressure and temperature of interest a

have, from (5.45):

SiO

melt

=µ

0,SiO

quartz

+RT ln



SiO

melt



(5.47)

and, using (5.46):



SiO

melt



=1. (5.48)

Another possibility is to define the standard state as pure liquid SiO

at the pressure and

temperature of interest. This standard state, µ

0,SiO

liquid

, is related to the pure quartz standard

state by:

0,SiO

liquid

=µ

0,SiO

quartz

+

P ,T

, (5.49)

where 

P ,T

is the Gibbs free energy of melting of quartz at the pressure and temperature

of interest, i.e. 

G for the reaction quartz → liquid SiO

at P and T. Using liquid SiO

the standard state and calling the activity relative to it a

we have:

SiO

melt

=µ

0,SiO

liquid

+RT ln



SiO

melt



(5.50)

255 5.5 Generalized equilibrium condition

and, using (5.46) and (5.49):



SiO

melt



=exp



−



P ,T



. (5.51)

Now, 

P ,T

vanishes only if P and T are on the melting curve of pure quartz, in which

case the two standard state chemical potentials are equal (equation (5.49)), and a

= a

Otherwise, it is 

P ,T

= 0 and a

= a

. Note very carefully that µ

SiO

melt

is the same in

(5.47) and (5.50). What has changed is the standard state, and therefore the activity scale

that measures this fixed chemical potential.

5.5.2 The equilibrium constant

Substituting (5.45)in(5.22), the condition of equilibrium among chemical species in an

arbitrary state and at temperature T can be written as follows:



0,i

+RT







=0. (5.52)

The first term of the sum in (5.52) is the standard state Gibbs free energy of reaction

(equation (5.7)):



0,i



0,i

P ,T

=

P ,T

, (5.53)

but this is now not necessarily zero, as equation (5.8) is true only for species in their

standard state, and we have relaxed this restriction. We define another non-dimensional

variable, called the equilibrium constant of the chemical reaction, and symbolized by K,

as follows:

K =







. (5.54)

Using (5.53) and (5.54)in(5.52) we get the following generalized equation of chemical

equilibrium:



P ,T

+RT ln K = 0. (5.55)

Finding the equilibrium position for a chemical reaction among species in any state entails

solving equation (5.55). This equation is a generalization of (5.8), and collapses to (5.8)if

all species are in their standard states, in which case, according to (5.45), it is a

= 1 for

all is, and, therefore ln K = 0. The following are two examples of equilibrium calculations

among solutions in heterogeneous and homogeneous systems.

256 Chemical equilibrium

Worked Example 5.3 The spinel–garnet transition in planetary mantles, part (ii)

In order to study phase changes in real planetary mantles we need to calculate the equilibrium

position of reaction (5.15) for the general case in which the Mg-bearing species are not pure

phases but components in mineral solid solutions. We define the standard state of each

Mg-bearing species as the pure crystalline solid (pyrope, forsterite, spinel or enstatite) at

the pressure and temperature of interest. Applying (5.54), we get the following expression

for the equilibrium constant of reaction (5.15):

K =

garnet

·a

SiO

olivine

MgAl

spinel



opx



. (5.56)

We then write the equilibrium condition (5.55) like this:



P ,T

+RT ln







garnet

·a

SiO

olivine

MgAl

spinel



opx









=0. (5.57)

Keeping in mind that 

P,T

is a function of P and T, given by (5.13), we see that (5.57)

contains six unknowns: P ,T and the four activities, which, as we shall discuss beginning

in the next section, are functions of composition. Therefore, equation (5.57) by itself has

five degrees of freedom, which means that in order to solve it we must specify the values

of five of the variables. We can ask (i) which five, and (ii) how? The answer depends on

what we are trying to accomplish. Let us look at two distinct possibilities.

Suppose first that we have a sample of lherzolite that contains the four-phase assem-

blage olivine–orthopyroxene–garnet–spinel, and that we have good reasons (petrographic

or other) to be confident that the four phases crystallized at equilibrium. We can then calcu-

late the four activities from the respective mineral compositions (more on this in subsequent

sections), leaving us with two unknowns in (5.57), and thus one degree of freedom. We are

now in the same situation that we discussed in Worked Example 5.1: we can calculate a

curve in P –T space that maps all the possible P –T combinations at which minerals with the

observed compositions could have crystallized. The location of this curve will in general be

different from the one in Fig. 5.5 (unless, by chance, activities are such that K = 1) and its

physical meaning is also subtly different (more on this in Chapter 6). The curve nonetheless

constrains the possible crystallization conditions of our lherzolite. If we have an indepen-

dent way of fixing one of the two variables, for instance temperature, then equation (5.57)

can be solved for the pressure of crystallization (subject to the uncertainties discussed in

Section 5.2.1, plus others that arise from activity–composition relationships, as we shall

see). We may label this procedure inverting mineral compositions in order to determine the

values of intensive variables during crystallization. It is also called “geothermometry” or

“geobarometry”, depending on which is the target intensive variable.

Alternatively, we may wish to do forward modeling in order to predict mineral compo-

sitions as a function of pressure and temperature. In this case we specify arbitrary values

of P and T, leaving us with three degrees of freedom in equation (5.57). In order to solve

the problem we need to come up with three additional equations, or some other way of

constraining three of the compositional variables (Worked Example 5.6).

257 5.5 Generalized equilibrium condition

Worked Example 5.4 Speciation in a homogeneous gas phase. Carbon–oxygen equilibrium,

part (i)

Carbon–oxygen equilibrium plays important roles in many planetary processes, from deter-

mining the composition of volcanic gases (Chapter 9) to determining ice compositions in

the outer reaches of the solar nebula, and perhaps the compositions of early post-nebular

atmospheres in terrestrial planets (Chapter 14). One often wishes to know the speciation in

the gas phase, i.e. the relative amounts of chemical species present in the gas phase, which

in this case would be CO

, CO and O

In almost every realistic speciation calculation in

planetary fluids a meaningful calculation requires that equilibria involving other system

components, chiefly hydrogen, nitrogen and sulfur, be included as well (more on this in

Chapters 9 and 14). The C–O example, however, allows us a simple first look into how the

calculations are carried out.

The following two equilibria describe the chemical reaction between carbon and oxygen:

Reaction 1: C+

←

→

CO,

Reaction 2: C+O

←

→

(5.58)

Let us assume that equilibrium is established in the presence of excess graphite, i.e. there

is not enough oxygen to oxidize all of the carbon. The assemblage then consists of graphite

and a gas phase composed of CO, CO

and O

. It is convenient in this case to define pure

graphite at the temperature and pressure of interest as the standard state for C, as this results

in: a

graphite

=1. We can now write one version of (5.55) for each reaction, as follows:

gas



gas



1/2

=exp



−



0,1

P ,T



(5.59)

and:

gas

=exp



−



0,2

P ,T



, (5.60)

where the 1 or 2 superscripts identify the reaction. If we specify pressure and temperature

then these are two equations in three unknowns (the three activities).The system of equations

appears to have one degree of freedom. We shall see, however, that we can recast the

activities as functions of the concentration, or mol fraction, of each of the three gas species

in the gas phase, X

, X

and X

. Solving for these concentrations is what we call

determining the speciation of the gas phase. If we assume that no other components are

present then we can write an additional equation which states that the gas contains only

, CO and O

: X

=1. Together with (5.59) and (5.60) this constitutes a

system of equations with no degrees of freedom, that we can solve for the three mol fractions

(at given P and T). We have not defined the standard states for the three gas species: O

,CO

and CO

. Neither the activities nor the Gibbs free energies of reaction in equations (5.59)

and (5.60) have any meaning unless standard states are specified. The usual way of defining

standard states for gases is different from condensed phases, and will be discussed briefly

in Worked Example 5.5, where we will solve equations (5.59) and (5.60), and in detail in

Chapter 9.