Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

268 Chemical equilibrium

taking R=Mg gives us the Mg-Tschermak’s end-member component: MgAlAlSiO

. The

two Al cations are kept separate in the formula to emphasize that they occupy different

crystallographic sites. In order to calculate the ideal activity of Mg-Tschermak’s we begin

by noting that the two octahedral sites in pyroxenes are distinct. One of them, labeled M1, is

smaller than the other one, M2. In a “perfect” orthopyroxene M2 sites are occupied by Mg

and Fe only. If such orthopyroxene dissolves Al then half of the Al cations enter the M1 site,

where they substitute for Mg or Fe cations, and the other half enter a neighboring tetrahedral

(T) site, where they substitute for Si. Because we assume that this coupled substitution

preserves local electrical neutrality the couples AlAl and MgSi behave as mixing units. In

a binary Mg–Al orthopyroxene (i.e., no Fe, Ca, etc.) the ideal activities of enstatite and

Mg-Tschermak’s in orthopyroxene are then given by equation (5.98):

MgTs,ideal

opx

Al,M1

Al,T

En, ideal

opx

Mg,M1

=1 −X

Al,M1

=1 −

(5.99)

where n

is the total number of Al cations per orthopyroxene formula unit: A

In the case of an Fe–Mg–Al orthopyroxene one possibility is that the coupled M1–T

substitution is independent of Fe–Mg substitution, and that Fe and Mg do not order

between M1 and M2 sites. The latter condition implies that (X

Mg,M1

)/(X

Fe,M1

) =

Mg,M2

)/(X

Fe,M2

) = n

, i.e. the ratio of Mg/Fe occupancy of M1 and M2 sites

equals the ratio between the number of Mg and Fe cations per orthopyroxene formula unit.

The following activity–composition expressions then follow from (5.96) and (5.98):

MgTs,ideal

opx

Al,M1

·X

Mg,M2

En, ideal

opx

Mg,M1

·X

Mg,M2

Fs,ideal

opx

Fe,M1

·X

Fe,M2

(5.100)

As an exercise, you should derive equations (5.100) formally starting from (5.70).

Worked Example 5.6 The spinel–garnet transition in planetary mantles, part (iii)

In Worked Example 5.1 we calculated a hypothetical location of the spinel–garnet tran-

sition by calculating the phase boundary for the Mg end-member reaction (5.15). This

phase boundary cannot be correct, as examination of natural peridotite samples shows that

orthopyroxene always dissolves some amount of Al. By (5.99), the activity of enstatite in

orthopyroxene must be less than 1, so that the equilibrium constant for reaction (5.15), given

by (5.56), does not vanish. Calling reaction (5.15) equilibrium (i), and using (5.99) for the

activity of enstatite, we re-write (5.57) as follows:



0,(i)

P ,T

−2RT ln X

Mg,M1

=0 (5.101)

since the activities of the other species remain unity. We can now write another reac-

tion, involving the Mg-Tschermak’s component in orthopyroxene, which we shall call

equilibrium (ii):

MgAl

+Mg

 MgAlAlSiO

+Mg

SiO

(5.102)

269 5.8 More complex ideal activity–composition relationships

the equilibrium condition for which is (see (5.99)):



0,(ii)

P ,T

+RT ln



Al,M1

Mg,M1



=0. (5.103)

Equations (5.101) and (5.103), together with the crystallographic constraint for a binary

Al–Mg orthopyroxene, X

Mg,M1

Al,M1

= 1, constitute a system of three equations with

one degree of freedom, as there are four unknowns: P , T , X

Mg,M1

, X

Al,M1

. We can specify

one of the variables, which in this case will be T, and solve the system of equations for the

other three variables, so as to obtain the location of the spinel–garnet phase boundary and

the composition of orthopyroxene as a function of temperature and pressure.

We begin by eliminating one of the mol fractions, say X

Al,M1

, and re-write (5.103)as

follows:



0,(ii)

P ,T

+RT ln



1 −X

Mg,M1



=0. (5.104)

We now have a system of two equations, (5.101) and (5.104), in three unknowns

(P , T ,X

Mg,M1

), which we solve by specifying temperature. The Maple implementation is

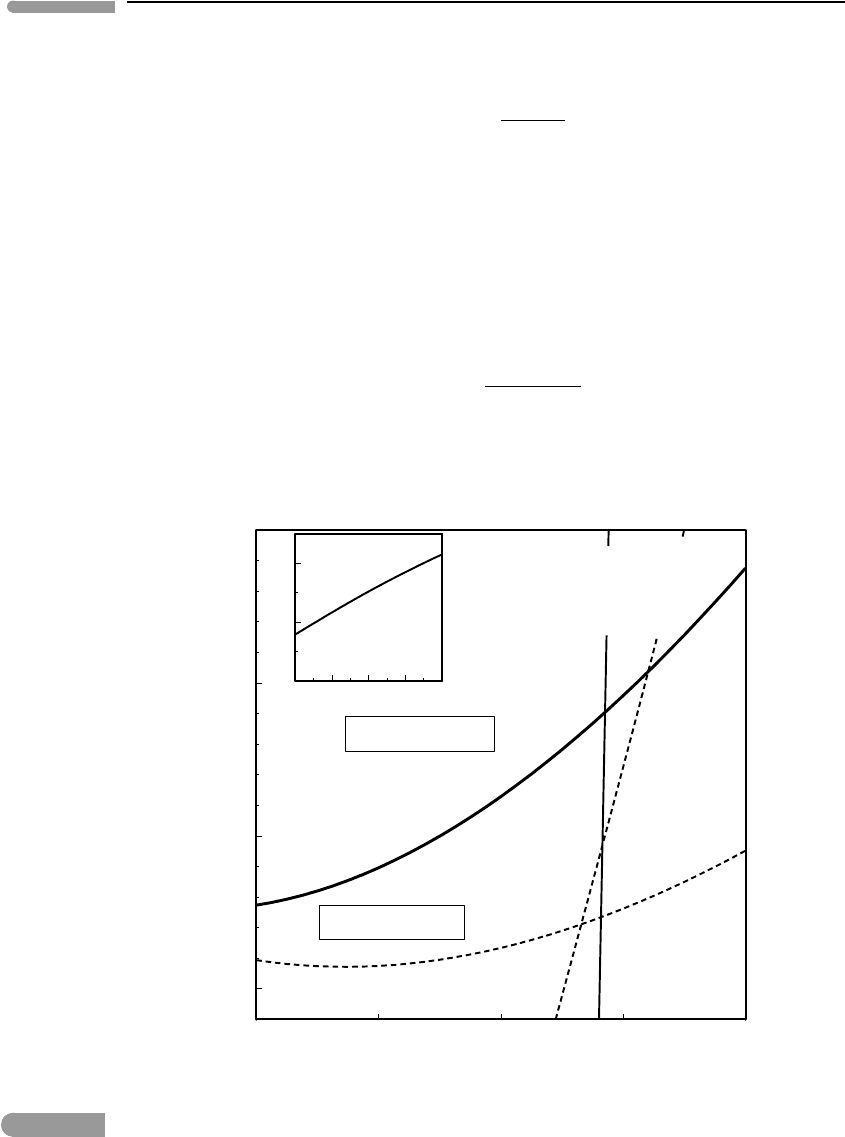
described in Software Box 5.4, and the results are shown in Fig. 5.10.

800 1000 1200 1400 160

Temperature (°C)

Pressure (kbar)

forsterite

pyrope

spinel + 2 aluminous enstatite

Garnet lherzolite

Spinel lherzolite

MOR adiabat

antle solidus

forsterite + pyrope

spinel + 2 enstatite

800 1000 1200 1400 1600

0.1

0.2

in enstatite

Fig. 5.10 Phase boundary between spinel lherzolite and garnet lherzolite calculated taking into account the Mg-Tschermak’s

component in orthopyroxene. The incorrect phase boundary from Fig. 5.5 (dashed line) is shown for comparison.

Predicted initial melting under mid ocean ridges shifts from the garnet to the spinel stability ﬁeld. Inset shows

calculated mol fraction of Al in orthopyroxene as a function of temperature (pressure is not constant in this graph).

270 Chemical equilibrium

Software Box 5.4 Calculation of spinel–garnet equilibrium, assuming ideal Al–Mg mixing in

orthopyroxene

The Maple worksheet sp_grt_MAS.mw contains a procedure named spgrAlMAS

that solves the two simultaneous equations, (5.101) and (5.104), for the two unknowns,

P and X

Mg,M1

in orthopyroxene. The two equations are labeled R1 and R2 in the Maple

procedure, which calls dGPT (see Software Box 5.2) to calculate the values of the stan-

dard state Gibbs free energy change of equilibria (5.15) and (5.102). Maple’s numerical

solver, fsolve, is quite powerful and is able to find solutions to systems of non-linear

equations with relative ease, as this example shows and as we shall have plenty of

opportunity to test in later chapters.

Because spinel–garnet equilibrium is relatively “flat” in P –T space the procedure

solves for pressure and orthopyroxene composition at a given temperature, for tempera-

tures over a range that is specified in the procedure call. The name of the file for output

is also specified in the procedure call. Output is: T −P −X

Al,M1

. Thermodynamic data

are stored in tab-delimited format in a file named spgrt. The procedure can be modi-

fied to calculate other equilibria, by changing and/or adding tables defining the required

reactions (e.g. reaction1, reaction2, etc.).

The calculated phase boundary is located at pressures 2–10 kbar higher than those

obtained assuming that there is no Al in opx (Fig. 5.5). Solubility of Al in orthopyrox-

ene increases with temperature (inset in Fig. 5.10), which agrees with the fact that the

right-hand side of reaction (5.102) has the higher entropy (exercise left for the reader). The

pressure shift arises because dissolution of Al causes the activity of enstatite to decrease

(equation (5.99)), so that its chemical potential decreases as well (equation (5.45)). Looking

Constant temperature

spinel + 2 enstatite

spinel + 2 aluminous enstatit

forsterite + pyrope

Pressure

Gibbs free energy

spinel lherzolite

garnet lherzolite

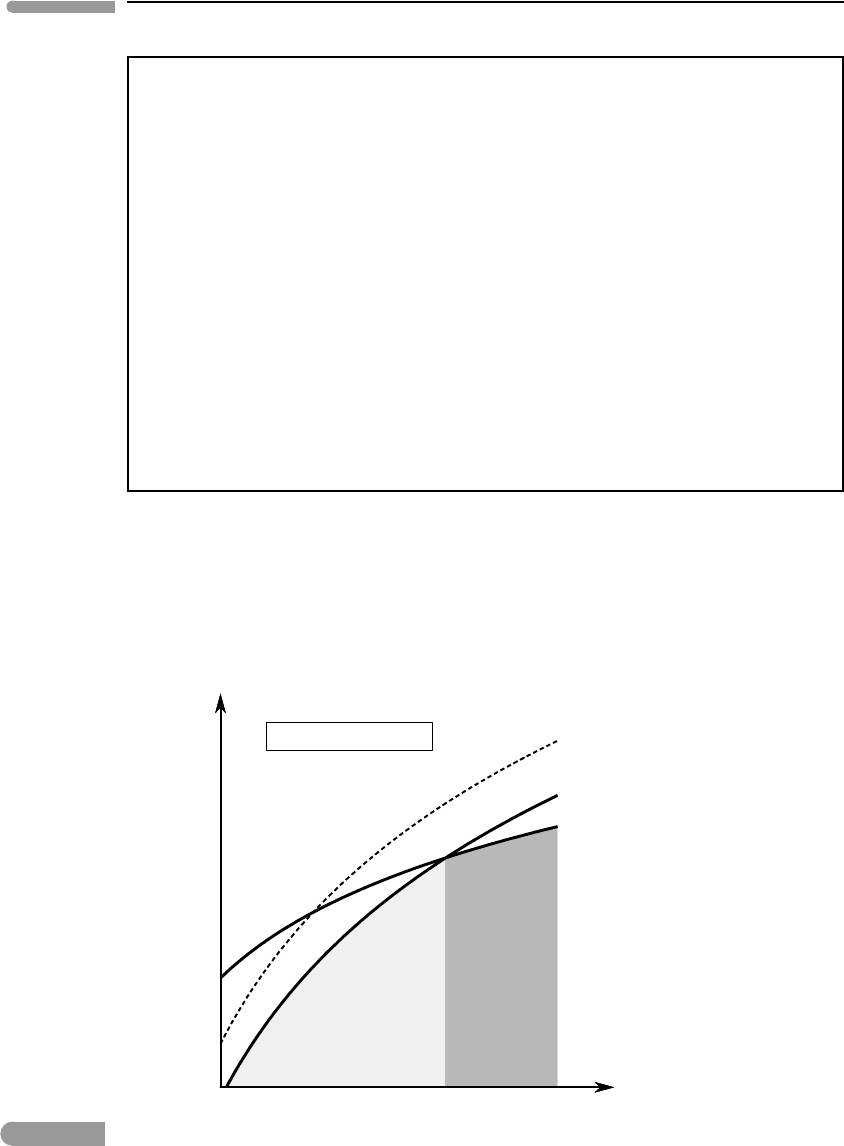
Fig. 5.11 Isothermal section across the Gibbs free energy surfaces for the assemblages in Fig. 5.10, showing that dissolution of

Al in orthopyroxene lowers the Gibbs free energy of the assemblage orthopyroxene +spinel, and must therefore shift

the equilibrium to higher pressure.

271 5.8 More complex ideal activity–composition relationships

at a schematic G–P diagram (Fig. 5.11), we see that lowering the Gibbs free energy of the

low-pressure assemblage in a reaction forces the equilibrium position to higher pressure.

This is a necessary consequence of the geometry of Gibbs free energy surfaces (Fig. 4.13).

The phase boundary in Fig. 5.10 is a better approximation than that in Fig. 5.5 to the con-

ditions under which the spinel–garnet transition takes place in planetary mantles, because

it accounts for the non-negligible solubility of Al in orthopyroxene. In contrast to what

we would have predicted if we had ignored the Al content of orthopyroxene, the more

complete phase diagram predicts that garnet becomes stable under mid-ocean ridges at

pressures of ∼24 kbar, and that MORB magmas form in the stability field of spinel lher-

zolites (Chapter 10). Our phase boundary in Fig. 5.10 is, however, still deficient on two

accounts. First, there are at least three other elements – Ca, Cr and Fe – that can be expected

to have non-trivial effects on the location of the spinel–garnet equilibrium. Second, our cal-

culations have been based on the assumption that crystalline solid solutions behave ideally,

but we have not examined the validity of this assumption.

5.8.2 Crystalline solutions with non-vanishing configurational entropy

in the end-member species

Because they can exist in several different states of cation ordering, plagioclase feldspars

are an excellent example of the effect of variable degrees of configurational entropy on

ideal activity. They also serve to illustrate further the use of equation (5.70). Using the

nomenclature from Worked Example 4.3, we recall that we can distinguish two T1 sites

and two T2 sites among the four T (tetrahedral) sites in one formula unit of feldspar. We

will consider mixing along the albite–anorthite join using three different assumptions about

cation ordering in the tetrahedral sites, as follows.

Model (i) assumes perfect local charge balance, such that Al–Si substitution only

occurs on T sites adjoining an octahedral site in which Ca–Na substitution occurs

simultaneously.

Model (ii) assumes that Al and Si mix randomly over the two T1 sites, so that the

two T2 sites are occupied by Si only. Mixing in tetrahedral and octahedral sites is

independent, so that there is no local charge balance.

Model (iii) assumes that Al and Si mix randomly over the four T sites, so that, again,

octahedral and tetrahedral mixing are independent and local charge balance is not

preserved.

The number of atoms of Na, Ca and Al, n

, n

and n

, per formula unit of plagioclase

and the mol fractions of Na and Ca, are related by the following equations:

=1 +X

=2 −X

(5.105)

The local charge balance model, case (i), corresponds to the simple example of coupled

substitution discussed in Section (5.8.1). For this model we therefore have:

Ab,ideal(i)

plg

An, ideal(i)

plg

(5.106)

In order to calculate the activities for model (ii) we must go back to equation (5.70) and

write out the number of microstates explicitly. Because octahedral and tetrahedral mixing

272 Chemical equilibrium

are now independent of one another the total number of microstates equals the product of

the numbers of octahedral and tetrahedral microstates:

Si,T1

. (5.107)

The number of Si atoms in the T1 sites is given by n

Si,T1

=2 −n

. Adding one molecule

of albite we find:

Ab+1

+1)!

+1)!n

Si,T1

+2)!

+1)!(n

Si,T1

+1)!

(5.108)

and similarly for one molecule of anorthite:

An+1

+1)!

!(n

+1)!

Si,T1

+2)!

+2)!n

Si,T1

. (5.109)

Substituting these equations in (5.70) and simplifying:

Ab,ideal(ii)

plg

Ab(ii)

Al,T1

Si,T1

(5.110)

and:

An, ideal(ii)

plg

An(ii)



Al,T1



. (5.111)

The mol fractions of Al and Si in the T1 sites are given by:

Al,T1

2 −X

1 +X

Si,T1

1 −X

(5.112)

We now note that for pure albite it is X

Al,T1

= X

Si,T1

, whereas for pure anorthite

Al,T1

=1. Substituting these values in (5.110) and (5.111), respectively, and recalling that

we require activities to be unity at the standard state (pure end-member species), we find

Ab(ii)

= 4 and C

An(ii)

= 1. With these values for the constants and mol fractions as in

(5.112) we obtain:

Ab,ideal(ii)

plg

(

)

(

2 −X

)

An, ideal(ii)

plg

(

1 +X

)

(5.113)

We follow the same procedure in order to calculate ideal activities for model (iii).

Equation (5.107) needs to be modified slightly, in order to reflect the fact that we must

now count all four silicon atoms, with n

=4 −n

. (5.114)

Adding one molecule of each end-member:

Ab+1

+1)!

+1)!n

+4)!

+1)!(n

+3)!

(5.115)

and:

An+1

+1)!

!(n

+1)!

+4)!

+2)!(n

+2)!

, (5.116)

273 5.8 More complex ideal activity–composition relationships

which, using (5.70) and simplifying, leads to:

Ab,ideal(iii)

plg

Ab(iii)

Al,T



Si,T



(5.117)

and:

An, ideal(iii)

plg

An(iii)



Al,T





Si,T



. (5.118)

The mol fractions of Al and Si over the four T sites are:

Al,T

2 −X

1 +X

Si,T

2 +X

3 −X

(5.119)

Unit activities at the standard state require that C

Ab(iii)

=256/27 and C

An(iii)

=16, so that

we finally arrive at:

Ab,ideal(iii)

plg

(

2 −X

)(

2 +X

)

An, ideal(iii)

plg

(

1 +X

)

(

3 −X

)

(5.120)

It is now clear that C

=1 if different cations mix on the same site in an end-member species,

as in this instance their mol fraction in the end-member species is not unity, but the activity

for the chosen standard state must be unity. From (5.63) we see that C

= 1 implies that

the entropy of mixing and configurational entropy of the solution are not the same, and we

can now understand why. The end-member plagioclase species may contain configurational

entropy that arises from Si–Al mixing in the tetrahedral sites (see also Worked Example 4.3),

and this entropy is “carried over” into the solution, so that it must be subtracted from the

total configurational entropy of the solution in order to obtain the net increase in entropy

generated by mixing.

The three sets of equations, (5.106), (5.113) and (5.120), yield significantly different

ideal activities for plagioclase of a given composition, but none of them is more “correct”

than any other. Choosing among the three models requires that one knows the structural

state of the particular plagioclase of interest. This is seldom trivial, and is complicated by

the fact that the two end-members may show different Al–Si ordering in their standard

states, as anorthite always has full long-range ordering (except perhaps near its melting

point) whereas the ordering state of end-member albite changes with temperature (see,

for example, Putnis, 1992). We will not discuss the details of configurational entropy in

plagioclase any further, but it is important to gain some insight into the energetic effects of

the different ideal activity models and their likely geological significance. This is shown

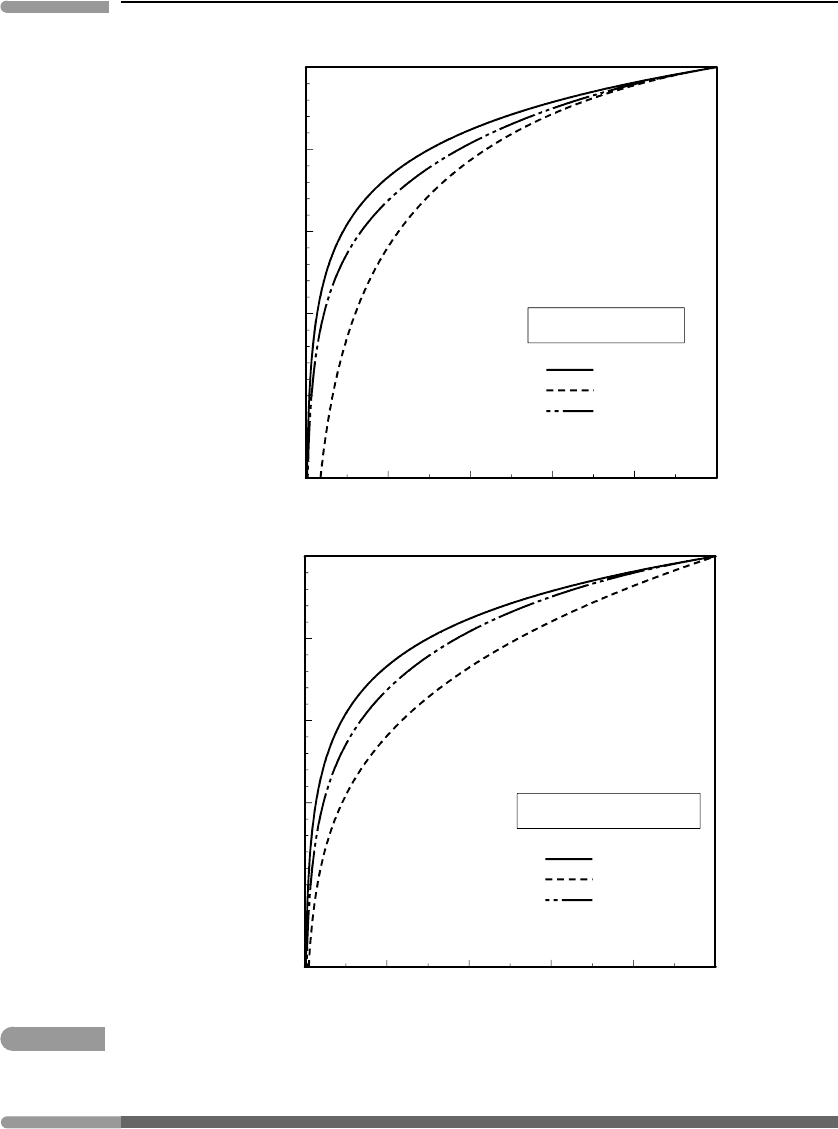
in Fig. 5.12, where we plot values of RT ln a

i, ideal

using T =1000 K as an example. The

calculated chemical potentials shift by the same amount as the energy difference between

models (equation (5.45)), and the effect is far from trivial. For example, a typical anorthite

content in plagioclase in medium to high-grade metamorphic rocks is An

20−40

. Figure 5.12

shows that the calculated chemical potential for anorthite would vary by 5–10 kJ mol

−1

depending on the ideal activity model used. Plagioclase in mantle rocks and in mafic igneous

rocks may contain ∼10–20% albite, and in this case the shift in calculated chemical potential

could be 20 kJ mol

−1

or more, as the temperature in such rocks is likely to be greater than

the 1000 K assumed in the figure. Energy differences of this magnitude would translate to

displacements in calculated equilibrium positions of hundreds of degrees or of kilobars to

perhaps tens of kilobars (see Section 5.2.1).

274 Chemical equilibrium

0 0.2 0.4 0.6 0.8 1

–50

–40

–30

–20

–10

TRnla

,bAlaedi

k(J lom

1–

)

Model (i)

Model (ii)

Model (iii)

0 0.2 0.4 0.6 0.8 1

–50

–40

–30

–20

–10

TRnla

,nAlaedi

k(J lom

1–

)

Model (i)

Model (ii)

Model (iii)

Albite, T = 1000K

Anorthite, T = 1000K

Fig. 5.12

Comparison of three ideal activity models for plagioclase, at a constant temperature of 1000 K.

5.9 Non-ideal solutions

We defined an ideal solution as one for which H

mixing

= 0. Ideal solutions have another

important property, which is that V

mixing

in them vanishes too, as is easy to prove starting

275 5.9 Non-ideal solutions

from (5.37) and (5.40). Ideal solutions are an algebraic construct based upon Boltzmann’s

postulate, but is it reasonable to expect that real substances will follow the ideal behavior

that is defined by the condition H

mixing

= V

mixing

= 0? There are physical reasons to

believe that in general this will not be the case. For example, molecules in some fluids

are polar (e.g. H

O), whereas in others they are not (CO

). When the two fluids mix

molecules screen electrostatic interactions among H

O molecules, and this should be

observed macroscopically as a non-zero V

mixing

. Different ions mixing in a crystalline

lattice generally differ in size, even if slightly, and therefore their surface charge densities

will differ too. Ionic substitution should then be accompanied by absorption or liberation

of energy (H

mixing

= 0), and perhaps by a change in volume relative to the equivalent

macroscopic aggregate (V

mixing

= 0). More subtly, mixing of different ions may have

effects on microscopic ordering that are not accounted for by the ideal mixing model, so

that the actual configurational entropy of the solution may be different from the value given

by (5.63). For example, ions may arrange themselves as if they are forming compounds (at a

microscopic level) and this will affect the configurational entropy of a crystal. Or molecules

may react to some extent in a mixed gas phase.

There are different ways of treating the behavior of real solutions. Here I focus on what

is perhaps the most widely used, and certainly the simplest, approach to real solutions. This

consists of assuming a reasonable microscopic mixing model from which one calculates

ideal activities, and then approximating the departure of the real (= observed) behavior

of the solution from this ideal model by fitting an empirical or semi-empirical function

with a variable number of free parameters. This is not the most elegant approach, as the

function has no strong physical justification, but there are a number of arguments that can

be made in its defense. Above all, it is simple and makes it possible to construct at least

a rough description of the behavior of real solutions on the basis of limited experimental

observations. Calibration of non-ideal solution models that have a better physical basis

often require experimental observations that for many phases and chemical species of

planetary interest do not exist. Their application to complex multicomponent phases under

very high temperatures and pressures may become computationally unwieldy, yet they

carry uncertainties that may make their results indistinguishable from those of simpler

empirical models, especially when compounded with possibly large uncertainties about

physical conditions in planetary interiors.

5.9.1 Excess mixing functions

Equation (5.91)(G

mixing

=H

mixing

−TS

mixing

) is valid for any solution, ideal or non-

ideal, as no assumptions about the nature of the solution were made in its derivation. If a

solution is non-ideal then in general it must be:

G

mixing

=G

ideal

mixing

. (5.121)

The inequality may arise from a combination of enthalpy and entropy contributions to

Gibbs free energy, but there may not be an a priori way of discriminating between them.

We therefore convert (5.121) into an identity by adding a Gibbs free energy contribution to

the Gibbs free energy of ideal mixing. This contribution is called excess Gibbs free energy,

excess

, and is defined by the following equation:

excess

≡G

mixing

−G

ideal

mixing

. (5.122)

276 Chemical equilibrium

∆G

mixing

∆G

mixing

∆G

mixing

∆G

mixing

(a)

(c)

(b)

(d)

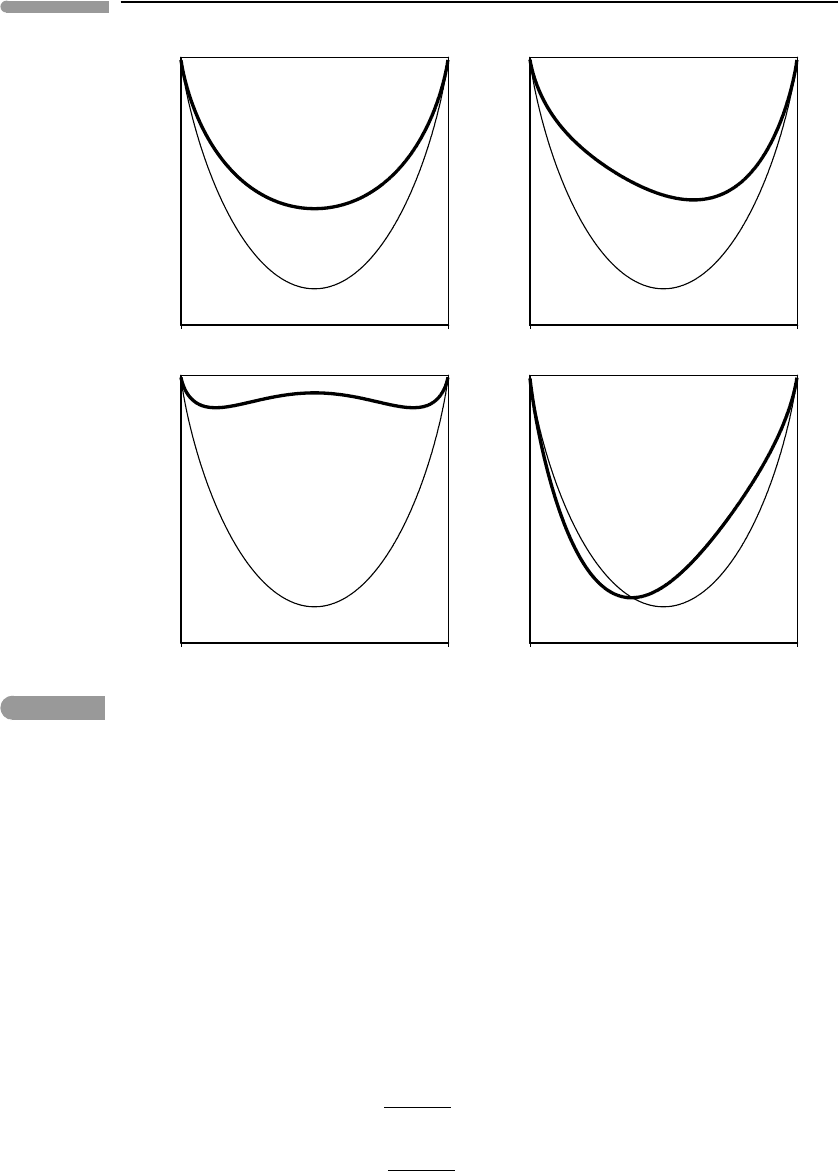
Fig. 5.13

Possible non-ideal behaviors of a binary one-site solution, shown by the thick curves. The thin curve is the same in all

four graphs and shows ideal one-site mixing. The examples shown do not exhaust all possibilities. For example, the

inﬂected behavior shown in (c) is symmetric, but it can also be asymmetric, as in (b). Negative deviation from ideality,

as in the left side of (d), can also be symmetric (at least in principle).

Figure 5.13 exemplifies possible behaviors of real solutions. The thick curves in the figure

represent the Gibbs free energies of four possible real solutions. The thin curves are the

Gibbs free energies of the same solutions, assumed to be ideal. The excess Gibbs free energy

is the distance between the curves. We see that G

excess

may be symmetric (Fig. 5.13a) or

asymmetric (Fig. 5.13b) relative to composition, it may be such that the curvature of the

G

mixing

function changes with composition (Fig. 5.13c), or such that the sign of G

excess

changes with composition (Fig. 5.13d), or some combination of these behaviors. Because it

is a Gibbs free energy, G

excess

is related to excess enthaply, entropy and volume functions:

excess

−T S

excess

(5.123)



∂G

excess

∂T



P ,n

=−S

excess

(5.124)



∂G

excess

∂P



T ,n

excess

. (5.125)

277 5.9 Non-ideal solutions

We use (5.2.12) to define a partial molar property, called excess chemical potential, µ

excess

as follows:

i, excess

≡G

excess

j=k



j=2



−X



∂G

excess

∂X

(5.126)

so that, by equation (5.29), G

excess



. From (5.126), (5.122) and (5.93) we get:

G

mixing



RT ln a

i, ideal



i, excess

(5.127)

and, by using (5.45):

−µ

0,i

=RT ln a

i, ideal

+µ

i, excess

. (5.128)

In order to construct a compact equation for the activity of a component in a non-ideal

solution we define a new non-dimensional parameter, called the activity coefficient and

symbolized by γ , as follows:

≡exp



i, excess



(5.129)

so that:

=γ

·a

i, ideal

. (5.130)

Equations (5.122) through (5.130) are the foundations of the mathematical treatment of

non-ideal solutions. They have a simple geometric interpretation which helps to visualize

the behavior of real solutions (Fig. 5.14). The excess chemical potential of a species is the

distance between the intersects of the tangents to the ideal and real Gibbs free energy of

mixing curves with the G axis for that species (compare Fig. 5.9). This distance vanishes

as the mol fraction of the species of interest approaches unity, and approaches a constant

finite value as the species becomes infinitely dilute (Fig. 5.14).

5.9.2 Raoult’s law and Henry’s law

If we consider a simple one-site binary solution then (5.130) becomes:

=γ

(5.131)

and, calling the two components 1 and 2, we get from (5.126):

1,excess

excess

−X

∂G

excess

∂X

. (5.132)

For X

→ 1 we have X

→ 0 and also G

excess

→ 0 (see Fig. 5.14), so that, as long as

∂G

excess

/∂X

stays bound, µ

1,excess

→0. We then have, for a nearly pure component:

, for X

→1. (5.133)

On the other hand, for X

→ 0, X

→ 1 but it is still G

excess

→ 0. Assuming again that

∂G

excess

/∂X

stays bound, we have:

1,excess

→0

=−



∂G

excess

∂X



. (5.134)