Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

278 Chemical equilibrium

0, b

RT ln

b, excess

excess

RT ln a

b, ideal

0, b

0, a

a, ideal

0, a

RT ln a

RT ln

a, excess

mixing

mixing, ideal

excess

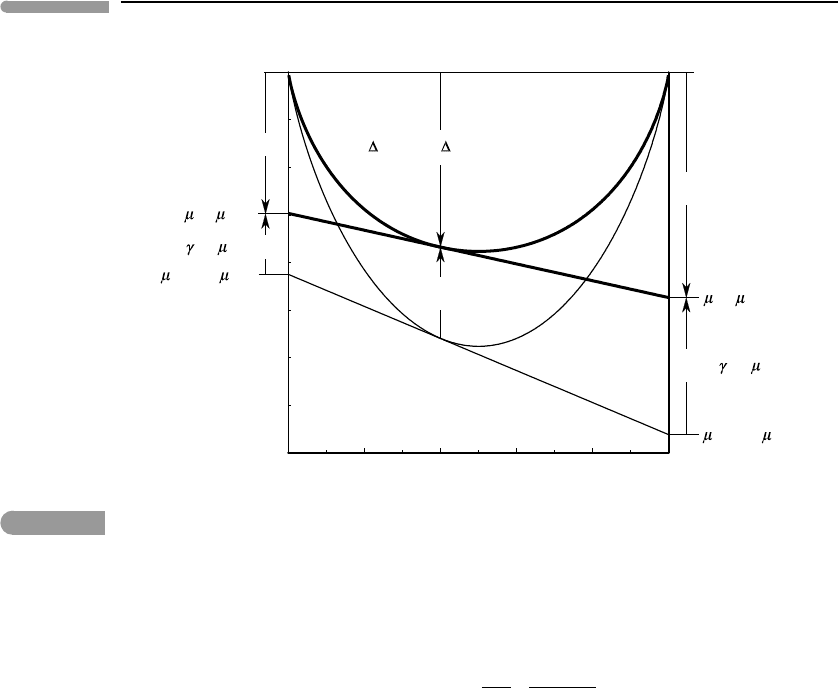
Fig. 5.14

Geometric interpretation of excess mixing properties. The thin curve and tangent line correspond to an ideal solution,

the thick ones to a (symmetric) non-ideal solution. Compare with Fig. 5.9.

We define a constant, K

, as follows:

=γ

→0

=exp



−



∂G

excess

∂X





, (5.135)

which, using (5.131), yields the following relation for an infinitesimally dilute component:

, for X

→0. (5.136)

Equations (5.133) and (5.136) are known as Raoult’s and Henry’s laws, respectively, and

were found empirically by the eponymous scientists during the nineteenth century. Raoult’s

law is perhaps self-evident, but Henry’s law is not. It requires that ∂G

excess

/∂X

approach

a constant finite value as X

becomes infinitesimally small.

Raoult’s and Henry’s laws were originally derived for binary mixtures of liquid and gases,

but they are applicable to any type of solution. For complex multi-site solid solutions we

can re-state them as follows:

i, ideal

, for X

→1 (5.137)

and:

i, ideal

, for X

→0. (5.138)

Henry’s law is the thermodynamic basis of trace element geochemistry (Chapter 10) and is

also important in the thermodynamic treatment of electrolyte solutions (Chapter 11).

279 5.9 Non-ideal solutions

5.9.3 Polynomial expansion of excess mixing functions

The empirical approach to describing non-ideal solutions consists of finding a function of

T, P and composition that can reproduce observed values of G

excess

(i.e., the varying dis-

tance between the curves in Fig. 5.13) as closely as possible. This function must subsume

Raoult’s and Henry’s laws. Thus, G

excess

must vanish as the end-member compositions are

approached, and all partial derivatives ∂G

excess

/∂X

must be finite over the entire compo-

sitional range, and in particular at the end-members. In addition to these two properties,

the G

excess

function must be such that it is able to reproduce a range of possible non-ideal

behaviors, as depicted in Fig. 5.13. A polynomial in powers of mol fractions can, subject

to some constraints, be made to do all of these things. The most general way of construct-

ing such a polynomial is to begin with the following series, in which the w coefficients

are constant with respect to composition but are in general functions of temperature and

pressure:

excess



ij k



ij kl

+···,

(5.139)

where i,j ,k,l, ... are solution components. Higher-order terms can be added as needed,

but it is often sufficient, or necessary owing to lack of data, to truncate the series after the

second term, in cubes of mol fractions.

A number of simplifications ensue. First, it is convenient to set coefficients with different

permutations of the same subindices equal to one another, i.e. w

= w

, w

ij k

= w

ikj

jik

jki

kij

kj i

and so on. Second, in order for G

excess

to vanish for all pure end-

member components every coefficient in which all subindices are the same must vanish too,

i.e. w

iii

iiii

=0, and so on if higher-order terms are included. Third, because of

the closure condition (



=1), there are dependencies among the non-zero coefficients,

which cuts down on the number of free parameters needed to fit G

excess

. This is easily seen

in a binary solution, but is true, although algebraically more complex, for solutions of any

number of components. Applying (5.139) to a binary solution, truncating the series at the

second term, collecting coefficients with different permutations of the same subindices and

omitting those coefficients that are zero we get:

excess

=2w

+3w

112

+3w

122

, (5.140)

which, noting that X

=1, we write as:

excess

[

112

+3w

122

+2w

(

)

]

(5.141)

or:

excess

[

(

112

+2w

)

(

122

+2w

)

]

. (5.142)

In equation (5.142) there are only two independent coefficients, which we are free to rename

as follows: W

= 3w

112

+ 2w

and W

= 3w

122

+ 2w

. These parameters, written

with a capital W , are commonly called Margules parameters or interaction parameters.

Equation (5.142) simplifies to:

excess





. (5.143)

280 Chemical equilibrium

The superscript G is added to the parameters to denote the fact that they measure excess

Gibbs free energy. It is important to realize that Margules parameters are functions of

temperature and pressure but not of composition.

We can verify that (5.143) is an acceptable algebraic representation of the excess Gibbs

free energy of a binary solution. First, G

excess

vanishes if the mol fraction of any of the two

end members becomes zero (Raoult’s law). Second, using infinitely dilute component 1 as

an example, we have:



∂G

excess

∂X



=−W

, (5.144)

i.e. ∂G

excess

/∂X

at the limiting end-member composition has a finite non-zero value and

is related to the Henry law constant by:

=γ

→0

=exp



−



∂G

excess

∂X





=exp





. (5.145)

There are no a priori conditions on the signs and relative magnitudes of the Margules param-

eters. An inflected G

mixing

curve (Fig. 5.13c) results if the two interaction parameters are

positive and large, whereas a G

excess

function that changes sign (Fig. 5.13d) arises if the two

parameters have different signs. An important simplification ensues if the two interaction

parameters are equal, in which case we have W

and:

excess

. (5.146)

Equation (5.146) corresponds to the symmetric behavior depicted in Figs. 5.13a and 5.13c,

whereas the general asymmetric case in Figs. 5.13b and 5.13d is reproduced by (5.143) with

= W

. A commonly used terminology refers to the symmetric solution described by

(5.146)asasimple mixture, and to the asymmetric solution given by (5.143)asasubregular

solution. To make things more confusing, a symmetric solution (=simple mixture) for which

excess

= V

excess

= 0 (i.e. for which G

excess

is independent of P and T) is called a regular

solution. I find this terminology, which is used primarily for historical reasons, unnecessarily

confusing, and will eschew it in favor of the more descriptive terms symmetric solution (e.g.

Fig. 5.13a and c) and asymmetric solution (e.g. Fig. 5.12b and d), with or without T and/or

P dependencies.

Because G

excess

is a linear function of interaction parameters, identities (5.123)to(5.125)

carry over to equivalent identities among interaction parameters, so that we have:

−TW

(5.147)



∂W

∂T



=−W

(5.148)



∂W

∂P



. (5.149)

Note that the subscript n

is no longer needed in the partial derivatives, because the interac-

tion parameters as defined by (5.139) are not functions of composition. Excess enthalpies,

entropies and volumes are calculated with (5.143)or(5.146), using W

, W

,orW

,as

needed.

281 5.9 Non-ideal solutions

Excess chemical potentials and activity coefficients are obtained by substituting the

polynomial expansion for G

excess

(i.e. equations (5.143)or(5.146), depending on whether

the solution is asymmetric or not) in (5.126) and (5.129). For example, for an asymmetric

binary solution we have:

1,excess



+2X



−W



. (5.150)

which for a symmetric solution simplifies to:

1,excess

. (5.151)

The attentive reader must have noticed that, beginning with equation (5.140), the dis-

cussion has focused exclusively on binary solutions. This is because the corresponding

polynomial expansions for solutions of three or more components quickly become much

more cumbersome, and are best dealt with by means of a symbolic algebra package such

as Maple (see end-of-chapter exercises).

5.9.4 Perils and tribulations of excess mixing functions

Whenever one uses non-ideal mixing models the fact must be kept in mind that the values

of excess thermodynamic properties are not independent of the values of standard state

properties. In order to understand what this means, and the perils that ensue, it is necessary

to sketch out how excess mixing properties are measured. One way of doing this is by

means of phase equilibrium experiments. The method is based on equilibrating a phase

of variable composition in an assemblage in which all the other phases are end-member

species that do not change composition. An example is the determination of Al–Mg excess

mixing properties in orthopyroxene using reaction (5.102). The experimental data that one

seeks are orthopyroxene compositions coexisting at equilibrium with end-member spinel

and forsterite. The equilibrium condition for this reaction is equation (5.103), which con-

tains three free parameters: P , T and X

Mg,M1

in orthopyroxene (e.g. equation (5.104)). If

we wish to determine the excess mixing properties of Al–Mg in orthopyroxene then we

can perform a series of phase equilibrium experiments at controlled pressures and temper-

atures, and measure the composition of orthopyroxene that crystallizes in each experiment.

Equation (5.103) assures us that at each P and T there is a unique equilibrium orthopyrox-

ene composition, since neither spinel nor olivine will depart from their Mg end-member

compositions. We will not go into the details of how the experiments are performed, what

are the uncertainties in experimental temperatures and pressures, how we can ascertain

whether equilibrium was attained in the experiments, or what are the likely uncertainties in

orthopyroxene compositions arising from analytical techniques (see for example Holloway

& Wood, 1988; Berman, 1988; Holland & Powell, 1998; Anderson, 2005). Rather, we will

put ourselves in the somewhat optimistic position that none of these is a concern, and see

that there is a more fundamental issue in play.

Allowing for the possibility that Al–Mg mixing in orthopyroxene may not be ideal, we

rewrite equation (5.103) as follows (see (5.128)):



0,(ii)

P ,T

+RT ln



Al,M1

Mg, M1



+µ

MgTs,excess

opx

−µ

En, excess

opx

=0. (5.152)

If we know the pressure and temperature of the experiment then we can calculate the standard

state Gibbs free energy of reaction (the first term in the equation), and we get the second term

(the ratio of ideal activities) from the measured orthopyroxene composition. One experiment

282 Chemical equilibrium

thus gives us the difference between the excess chemical potentials of Mg–Tschermakite and

enstatite. We will see in a second that with multiple experiments we can find the absolute

value of each of the excess chemical potentials, but before getting into that you must

understand that equation (5.152) is the crux of the issue: the values of the excess chemical

potentials are anchored to the values of the standard state thermodynamic properties. The

problem is that standard state properties for many species of interest in the planetary sciences

are not known with high accuracy, and there may be significant differences among values

given in different data bases. Excess mixing properties measured by phase equilibria are

relative values. They are determined relative to standard state properties from a specific

data base, and they can ONLY be used together with standard state data from that same data

base. Of course, equation (5.152) shows that the values of excess mixing properties are also

anchored to our choice of ideal activity model, but accounting for this is less of a problem,

as it requires only that one be consistent when calculating ideal activities. In contrast,

combining excess properties with standard state properties different from those used in the

derivation of the excess properties renders the results questionable at best. Excess mixing

properties can also be derived from calorimetric measurements (see Navrotsky, 1986), and

although these can be absolute values, the same caveat applies: they should not be used in

conjunction with standard state properties derived by some other method.

Extracting Margules parameters from (5.152) is straightforward but requires that we per-

form multiple experiments over a range of pressures and temperatures, so as to obtain a range

of orthopyroxene compositions. Assuming that Mg–Al non-ideal mixing is asymmetric, we

use (5.150) to re-write (5.152) as follows:



0,(ii)

P ,T

+RT ln



Al,M1

Mg,M1



AlMg



Mg,M1

−2X

Al,M1

Mg,M1

−2X

Mg,M1

Al,M1



−W

MgAl



Al,M1

−2X

Al,M1

Mg,M1

−2X

Mg,M1

Al,M1



=0.

(5.153)

This is one equation in two unknowns (the two Margules parameters). In principle, and

assuming that there is no temperature nor pressure dependency of the W

parameters

(i.e. W

= W

= 0, see equations (5.148) and (5.149)), with two experiments at different

conditions, in which the values of 

, X

and X

are different, we could solve for the

two parameters. In practice many experiments are required so as to have an overdetermined

system of equations that allows us to analyze experimental errors, and detect possible P and

T dependencies of the Margules parameters (i.e. discriminate W

into W

, W

and W

see equation (5.147)). Assuming a symmetric solution simplifies 5.153 considerably, to:



0,(ii)

P ,T

+RT ln



Al,M1

Mg,M1





Mg,M1

−X

Al,M1



=0. (5.154)

One commonly uses experimental data to test for symmetry vs. asymmetry, for example

by determining whether the difference between the two parameters fitted to an asymmetric

model is statistically significant.

The following example is designed to show that, no matter what model one chooses to

use to represent the behavior of a real solution, unless consistency between the various

sources of thermodynamic data is observed, the results can be spectacularly incorrect.

283 5.9 Non-ideal solutions

Worked Example 5.7 The spinel–garnet transition in planetary mantles, part (iv)

The spinel–garnet transition can be used as an example of the perils of combining mixing

and standard state properties that are not consistent with one another. The phase boundary

andAl contents in orthopyroxene in Fig. 5.10 were calculated using standard state properties

from Holland and Powell (1998) and ideal Al–Mg mixing in orthopyroxene. Relative to

their standard state properties, Holland and Powell find that W

AlMg

= 0. In other words,

Al and Mg appear to mix ideally in orthopyroxene. In truth what probably happens is that

the available experimental data are too sparse and do not make it possible to accurately

discriminate between standard state and excess mixing properties for this particular binary

join. The safest course of action in such case is to set the excess chemical potential equal to

zero, and let the standard state properties of Mg–Tschermakite “absorb” any excess mixing

properties – this is, I believe, what Holland and Powell have done. Whether or not Al–Mg

mixing in orthopyroxene is ideal, and it almost certainly is not, if we are going to use Holland

and Powell’s standard state properties to calculate the phase boundary then we must use

ideal mixing. The curves in Fig. 5.10 are therefore the correct ones.

800 1000 1200 1400 160

Temperature (°C)

Pressure (kbar)

forsterite

+ pyrope

spinel

+ 2

aluminous

enstatite

forsterite

pyrope

spinel

enstatite

800 1000 1200 1400 1600

0.1

0.2

in enstatite

forsterite

pyrope

spinel

aluminous

enstatite

CONSISTENT

INCONSISTENT

CONSISTENT

INCONSISTENT

Fig. 5.15 The effect of calculating a phase boundary using excess mixing properties that are inconsistent with the standard

state properties. Curves labeled “CONSISTENT” were calculated using standard state properties from Holland and

Powell (1998), that require that Al–Mg mixing in orthopyroxene be considered ideal. Curves labeled “INCONSISTENT”

were calculated with the same standard state properties, and Al–Mg excess mixing properties from Klemme and

O’Neill (2000b). This does not mean that Klemme and O’Neill’s mixing properties are incorrect, only that they are

anchored to a different set of standard state properties. The purpose of the diagram is to show that using standard

state and mixing properties that are inconsistent with one another can engender very signiﬁcant errors.

284 Chemical equilibrium

Perusing the literature, however, one finds other studies that report significant non-ideality

for Al–Mg mixing in orthopyroxene. One such paper is the one by Klemme and O’Neill

(2000b), who find a symmetric non-ideal behavior with W

=20 kJ mol

−1

, but relative to

a different set of standard state values (which unfortunately they do not make explicit). Let

us ignore this “but” and recalculate the phase diagram using Holland and Powell’s standard

state data and Klemme and O’Neill’s non-ideal mixing model. The calculation is very

easily implemented in Maple (Software Box 5.5) and the results are shown in Fig. 5.15.

The calculated phase boundary shifts by ∼5 kbar, and the calculated Al mol fraction in

orthopyroxene drops by about 0.1 to 0.15. These are non-negligible displacements, and the

new curves (labeled “INCONSISTENT” in the figure) are incorrect. Note that this does

not mean that Klemme and O’Neill’s non-ideal mixing model is incorrect. Their model is

a different way of allocating experimental measurements among standard state and excess

properties, as equation (5.152) should make clear. This exercise is designed to demonstrate

the fallacy of combining excess properties and standard state properties that are not mutually

consistent. I emphasize: I made this error on purpose, with purely didactic goals.

Software Box 5.5 Incorporation of non-ideal Al–Mg mixing in orthopyroxene to the calculation

of spinel–garnet equilibrium

The Maple worksheet sp_grt_MAS.mw contains a procedure named

spgrAlMASni that adds non-ideal mixing terms to equations (5.101) and (5.104).

Assuming symmetric non-ideal Al–Mg interactions in orthopyroxene, we find from

equation (5.151):

En, excess

opx

AlMg

(5.155)

and:

MgTs,excess

opx

AlMg

. (5.156)

Incorporating these excess chemical potentials in (5.101) and (5.104), and recalling that

Al,M1

Mg,M1

=1, we get:



0,(i)

P ,T

−2RT ln X

Mg,M1

−2W

AlMg



1 −X

Mg,M1



=0 (5.157)

and:



0,(ii)

P ,T

+RT ln



1 −X

Mg,M1



AlMg



Mg,M1

−



1 −X

Mg,M1





=0.

(5.158)

As in the ideal solution case (Software Box 5.4) we have two equations that, if we

fix temperature, we can solve for the two unknowns, P and X

Mg,M1

in orthopyroxene.

Procedure spgrAlMASni is thus otherwise identical to spgrAlMAS.

In the example discussed in Worked Example 5.7 I have purposely used values of

standard state and excess mixing properties that are inconsistent with one another. Of

course, the Maple procedure can be used with any combination of thermodynamic prop-

erties, by modifying the standard state values stored in the spreadsheet RefStateData

and/or the value of the excess mixing parameter stored in the variable WAlMg.

285 Exercises for Chapter 5

Exercises for Chapter 5

5.1 Calculate the Clapeyron slope for the reaction spinel + 2 enstatite

→

←

forsterite +

pyrope at 298 K and 1 bar, and compare your result to the slope of the reaction in

Figure 5.5.

5.2 Using the reaction spinel + 2 enstatite

→

←

forsterite + pyrope, verify that the assem-

blage with higher entropy is the one that is on the high temperature side of the phase

boundary, and the assemblage with higher density is on the high pressure side of the

phase boundary.

5.3 Calculate the phase boundary for the transition between plagioclase lherzolite and

spinel lherzolite for the end-member Ca–Mg system, assuming that both diopside

and enstatite remain as pure end-member phases, and ignoring the order–disorder

transition in anorthite (more on this in Chapter 7). You need to write a balanced

reaction among anorthite, forsterite, diopside, enstatite and spinel, and program this

reaction in the Maple worksheet th_template_3.mw (see Software Box 5.2).

Use standard state properties from Holland and Powell (1998). You will refine this

calculation in Exercises 5.15 through 5.17.

5.4 Calculate the activity of diamond relative to the standard state graphite, and the activity

of graphite relative to the standard state diamond, at 298 K and 1 bar. What is the

physical meaning of a>1? Of a<1?

5.5 Show that the conclusion that chemical species are transferred down chemical poten-

tial gradients (i.e. equation (5.26)) is valid in systems with any arbitrary number of

phases and components.

5.6 Prove equations (5.95), starting from (5.70).

5.7 Prove equations (5.97), starting from (5.70).

5.8 Prove equations (5.100), starting from (5.70).

5.9 Write equations for the ideal activities of eastonite (KMg

AlAl

(OH)

) and

muscovite (KAl

AlSi

(OH)

) in a trioctahedral mica.

5.10 Prove equation (5.91), i.e.:

G

mixing

=H

mixing

−TS

mixing

5.11 Prove that V

mixing

for an ideal solution is zero.

5.12 Use Maple’s plotting capabilities to explore the conditions under which a non-ideal

symmetric solution develops an inflected G

mixing

curve, as in Fig. 5.13c. (Hint: vary

the relative values of temperature and the interaction parameter.)

5.13 Use Maple’s plotting capabilities to show that a G

excess

function for an asymmetric

solution that changes sign (as in Fig.5.13d) arises only if the two interaction parameters

have different signs.

5.14 Prove equation (5.150).

5.15 A first step in refining the anorthite–spinel phase boundary in lherzolites is to include

the Mg–Tschermak’s component in orthopyroxene (using reaction (5.102)) and the

Ca–Tschermak’s component in clinopyroxene: CaAlAlSiO

. Assume that Ca fills the

M2 site incpx, and thatAl and Mg mix in the M1 site of cpx, as in opx.You need to come

up with an additional balanced chemical reaction that includes the Ca–Tschermak’s

species in cpx. There are several possibilities, but the simplest one is a reaction among

the two Tschermak’s components, diopside and enstatite. You will end up with three

linearly independent equations ((5.102), the one that you derived in Exercise 5.3, and

286 Chemical equilibrium

your new reaction) in four unknowns: P, T,(X

Al,M1

)

opx

and (X

Al,M1

)

cpx

. The system

has one degree of freedom, and can be solved by fixing one variable, for example

temperature. Use the discussion in Software Box 5.4, and the worksheet described

there, to help you program the solution of this system of equations in Maple, assuming

ideal mixing in both pyroxenes. Plot the new plagioclase–spinel phase boundary and

compare it with the one you generated in Exercise 5.3. Use standard state properties

from Holland and Powell (1998).

5.16 In order to further refine the plagioclase–spinel phase boundary you should include

excess mixing properties in pyroxenes. According to Holland and Powell, Al–Mg

mixing in the M1 site of both pyroxenes is symmetric, with (W

AlMg

)

opx

= 0 and

AlMg

)

cpx

=7 kJ mol

−1

. With the discussion in Software Box 5.5 as a guide, include

the corresponding excess chemical potentials, recalculate the plagioclase–spinel phase

boundary and compare it with the ones you generated in Exercises 5.3 and 5.15.

5.17 In reality, Ca and Mg also mix in the M2 site of both clinopyroxene and orthopyroxene.

You can then add the following two reactions to your system of equations:

(CaMgSi

)

cpx

→

←

(CaMgSi

)

opx

(Mg

)

cpx

→

←

(Mg

)

opx

and end up with a system of five equations and six unknowns: P , T ,(X

Al,M1

)

opx

Al,M1

)

cpx

,(X

Mg,M2

)

opx

, and (X

Mg,M2

)

cpx

. The system still has one degree of free-

dom, and can thus be solved by fixing one variable, e.g., temperature. According to

Holland and Powell, Ca–Mg mixing in the M2 site of pyroxenes is symmetric, with

CaMg

)

opx

=(W

CaMg

)

cpx

= 30 kJ mol

−1

. Recalculate the plagioclase–spinel phase

boundary and compare it with the ones you generated in Exercises 5.3, 5.15 and 5.16.

Phase equilibrium and phase diagrams

A phase diagram is a graph that shows the distribution of stable phase assemblages as a

function of the values of the intensive variables used to describe the thermodynamic system.

If pressure and temperature are the variables of interest then the stable assemblage is the

one with the lowest Gibbs free energy, although other thermodynamic potentials may be

used if the variables of interest are different, for example, Helmholtz free energy if one

is interested in temperature and volume (more on this in Chapter 9). Phase diagrams are

powerful analytical tools in many branches of planetary sciences, as they provide a way

to quickly visualize how phase assemblages change in response to changes in pressure,

temperature, chemical potentials, or any other combination of intensive variables. There

are many different types of phase diagrams and it is not the purpose of this book to offer a

comprehensive review of all of them. Rather, in this chapter I will focus on the fundamental

rules that phase diagramsmust abide by inorder to be thermodynamicallyvalid.We therefore

begin with a discussion of the thermodynamic underpinnings of phase diagrams.

6.1 The foundations of phase equilibrium

6.1.1 The Gibbs–Duhem equation

Any extensive thermodynamic property can be written as a sum of products of partial molar

properties times mol numbers (equation (5.27)). Let us re-write equation (5.27) specifying

the identity of the phase that it applies to with the index α (α can be a solution or a pure

phase, in which case identity (5.27) is trivial):



. (6.1)

Taking derivatives:



. (6.2)

Now, since Z is a state variable it is a function of temperature and pressure, i.e. the following

function exists:



P , T , n



. (6.3)

287