Douce A.P. Thermodynamics of the Earth and Planets
Подождите немного. Документ загружается.


178 Energy transfer processes in planetary bodies
that are so diametrically opposed – i.e., are they rising or sinking? – that it should be possible
to come to some resolution on the basis of available observations.
In the case of Mars (Fig. 3.19), the response of the lithosphere to the load of the large
volcanoes indicates that the mean thickness of the planet’s rigid lid is of the order of a few
hundred kilometers, which is compatible with both end-member steady-state models. A
mantle heat flux of 30 mW m
−2
(see Box 3.2), which could account for most of the Martian
heat output, implies a lithosphere ∼200 km thick and mantle temperatures some 500–700 K
higher than on Earth, depending on the assumed mantle viscosity (thin dashed line in the
center panel). This is probably at odds with the apparent paucity of active volcanism on
Mars. If, as seems likely, the surface layers of the planet are enriched in incompatible
elements then the mantle heat flux could be significantly lower than 30 mW m
−2
. Mantle
heat flux for a 700-km thick, 4 billion year old lithosphere could be around 10 mW m
−2
(center panel). Even in this case mantle temperature could be 200–500 K higher than in
the Earth and the deep mantle would still be convecting, with a Rayleigh number of ∼ 10
6
(bottom panel). This suggests the idea that Mars is an agonizing planet that is not quite dead
yet (with apologies to Monty Python). Yes, most of its surface is old and heavily cratered,
but huge volcanoes here and there were active as recently as 160–200 Ma, perhaps more
recently, marking a few places where the hot and actively convecting mantle was able to
poke through the 700-km thick lithosphere.
Exercises for Chapter 3
3.1 In Section 2.1 I described the reason why heat flux in solid planetary bodies other
than Io cannot be estimated remotely, and must be measured with direct observation
on the ground. Use Fourier’s law to design an experiment to measure the natural heat
flux of rocky planetary bodies.
3.2 Consider a sequence of parallel rock layers that differ in their thermal conductivities.
Assume that there is no heat production in any of the layers. Define the condition for
steady state heat flow across the sequence. Steady state means dT/dt = 0 everywhere.
3.3 Assume that all the layers in Exercise 3.2 have the same thickness. What is the factor
that determines steady-state heat flow across the system? Generalize your criterion to
a system in which the layers are of arbitrary thickness.
3.4 Draw schematic but geometrically correct plots of the steady-state geotherm for
(a) a lithosphere with no heat generation, (b) a lithosphere with a heat source (e.g.
radioactive decay) and (c) a lithosphere with a heat sink (e.g. melting).
3.5 Calculate and plot the thickness of the oceanic lithosphere as a function of the age of
the ocean floor, for ages ranging from 20 to 200 million years. Let κ = 10
−6
m
2
s
−1
,
and assume that there is no heat production in the oceanic lithosphere.
3.6 Using your results from Exercise 3.5, calculate and plot the thickness of the oceanic
lithosphere as a function of distance from the mid ocean ridge, for the Atlantic Ocean
(spreading rate ≈ 2 cm year
−1
) and for the Pacific Ocean (spreading rate ≈ 10 cm
year
−1
).
3.7 Using your results from Exercise 3.6, plot heat flux through the ocean floor as a
function of age of the ocean floor. Assume k = 3Js
−1
m
−1
K
−1
, temperature at the
base of the lithosphere = 1400
◦
C, temperature at the ocean floor = 0
◦
C.

179 Exercises for Chapter 3
3.8 Discuss why it is not possible to use the approach in Exercises 3.5 to 3.7 to calculate
continental heat flux.
3.9 In the definition of heat diffusivity the product (ρc
P
) describes the thermal inertia of
the material. What is the dimension of ρc
P
? Comment on this.
3.10 How long will it take for each of the following to cool to ambient temperature? (i)
A lava flow 10 m thick. (ii) A 10-m thick sill emplaced at a depth of 2 km. (iii) A
pyroclastic layer 10 cm thick. (iv) A granitic pluton with a 10 km diameter.
3.11 In Section 2.4 we assumed that the temperature distribution inside an accreting planet
is not modified by heat flow during the accretion process. Justify this assumption for
accretion times of 10
5
to 10
7
years.
3.12 What is the maximum asteroid size for which we can be certain that cooling is com-
plete? What can you say about cooling of asteroids larger than this? For an asteroid
larger than this size, how would you determine whether or not it is still cooling down?
3.13 In Section 2.9 we saw that decay of short-lived isotopes may liberate enough thermal
energy to melt a chondritic asteroid in 1–10 million years. Discuss whether there is
some relationship between the size of the asteroid and the likelihood that it will melt by
this process. Derive an approximate relationship between accretion rate and half life
and concentration of a short-live isotope that may allow you to make semi-quantitative
predictions about melting of planetesimals in the very early Solar System.
3.14 Derive the equation for the adiabat on a P–V diagram (Fig. 3.9).
3.15 Calculate the dry adiabatic lapse rates for the five solid planetary bodies with “sub-
stantial” atmospheres: Venus, Titan, Earth, Mars and Triton. Look up the necessary
data in Lodders and Fegley (1998). For each case, discuss whether or not the dry adi-
abatic lapse rate is a good approximation to the temperature structure of convective
atmospheric layers.
3.16 Modify equations (3.36)or(3.37) to include the effect of condensation of atmospheric
species (e.g. H
2
O in Earth or CH
4
in Titan). This is known as the wet adiabatic lapse
rate. (Hint: start from equation (3.27), but now dQ = 0. Write dQ in terms of latent
heat and mass of vapor that changes state).
3.17 Estimate the minimum thickness of a thrust sheet in which Buchan metamorphism
can develop, and show why blueschist metamorphism can develop in accretionary
wedges. (Hint: start from equation (3.49)).
3.18 Discuss the Gulf Stream and the Hudson current from the point of view of the Péclet
number of the ocean.
3.19 Aglacier advects enthalpy from the zone of ice accumulation to the zone of ablation. If
we consider a steady-state atmosphere then the terminus of the glacier can be thought
of as being located at a point where the temperature perturbation caused by exposure
to air warmer than that in the zone of accumulation has been able to penetrate the
entire thickness of ice. Derive an equation that relates the length of a glacier to its
thickness and flow rate. Test your equation by comparing its predictions with observed
dimensions and flow rates of alpine and continental glaciers. Discuss possible sources
of discrepancies. For ice κ = 1.5 × 10
−6
m
2
s
−1
.
3.20 In the accretion model (Section 2.4) we ignored compression of the growing planet.
Derive an equation for temperature increase in the planetary interior caused by
adiabatic compression. What is the source of this thermal energy?
3.21 Decide whether icy satellites convect. Assume that they are composed of H
2
O ice,
for which: µ =10
12
Pa s, κ = 1.5 ×10
−6
m
2
s
−1
, α =2 ×10
−4
K
−1
and ρ
0
=1000
kg m
−3
. Consider and justify a range of likely values for T (temperature drop across

180 Energy transfer processes in planetary bodies
the thermal boundary layer). You may want to analyze separately the cases of large
satellites (e.g. Callisto) and small ones (e.g. Mimas or Enceladus). Necessary data not
listed above can be found in Lodders and Fegley (1998).
3.22 Discuss whether the large asteroid Vesta may have convected, whether it is likely to be
convecting now, and how long convection may have lasted. Use material properties
for silicate planets given in the text (e.g. Figure 3.15), and other necessary data from,
yes, Lodders and Fegley (1998).
3.23 Estimate ranges of possible convective velocities in Venus and Mars. Compare your
results with the velocity of terrestrial mantle convection and discuss the physical
reasons for the differences.
3.24 Io has an observed heat flux of ∼ 2.5 W m
−2
. Assuming that Io is undergoing steady-
state stagnant lid convection, estimate the thickness of, and temperature difference
across, the thermal boundary layer, and the velocity of Ionian convection. Are your
results likely? If not, how can Io’s heat flux be accounted for?

4
The Second Law of Thermodynamics and
thermodynamic potentials
The First Law of Thermodynamics, like all conservation laws, is expressed mathematically
by an identity relationship. As such, it is incapable of predicting the direction in which a
natural process will occur. For example, on the basis of energy conservation alone it is not
possible to decide whether heat flows from a hot body to a colder one, or the other way
around. We know that heat flows down a temperature gradient, but this does not follow from
the First Law. Similarly, energy conservation cannot predict that ice will melt at 20
◦
C, or
that water will freeze at −20
◦
C, and it cannot predict that a gas will expand to fill all of
the volume available to it.
Another law of nature is required to predict the direction of spontaneous changes. By
“spontaneous” we mean a process that occurs in nature in the direction towards equilibrium
and without outside intervention. For example, heat flow down a temperature gradient is a
spontaneous process. It is possible to transfer heat from a cold body to a hotter one, but this
requires “outside intervention” in the form of a heat pump, which uses mechanical energy
to accomplish a process that is not “naturally spontaneous”. As soon as the expenditure of
mechanical energy ceases the spontaneous process takes over and the cold body heats up
at the expense of the hotter one.
The law that we are searching for,which is the Second Law ofThermodynamics, cannot be
expressed by a mathematical identity, because identities are unable to determine direction.
Therefore, it cannot be a conservation law. Rather, the Second Law of Thermodynamics
must be a law that states that some quantity changes when a spontaneous process takes
place, or, equivalently that the total content of some quantity in the observable universe
varies monotonically with time.
4.1 An intuitive approach to entropy
Consider two bodies at different temperatures, T
1
>T
2
, enclosed in a container that is a
perfect thermal insulator, is also perfectly rigid (i.e. it cannot undergo expansion work) and
is impervious to any other imaginable type of energy transfer. The system (in this case, our
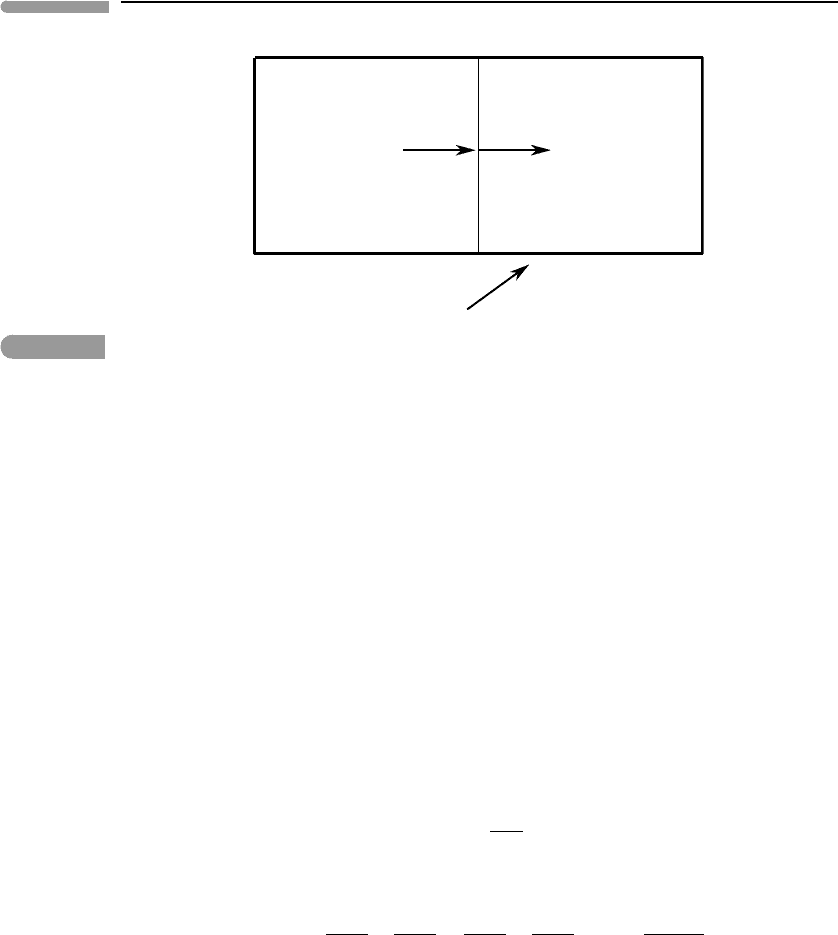
two bodies) enclosed in such a container is called isolated (Fig. 4.1). Recall that adiabatic
means impervious to heat transfer, but not to exchanges of mechanical energy. We know
that heat will flow from body 1 to body 2 until their temperatures become the same, at
which point heat transfer will stop. Heat does not spontaneously flow from a cold body to
a hotter one. This is an observation as fundamental, and as impossible to demonstrate from
simpler concepts, as any conservation law, such as those for energy, momentum or electric
charge. It is, in fact, one possible statement of the Second Law of Thermodynamics.
The First Law of Thermodynamics applied to our system goes as follows. Let us assume
that the coefficients of thermal expansion of the two bodies are zero, so that there is no
181
182 The Second Law of Thermodynamics
∆Q
1
∆Q
2
T
1
T
2
rigid & insulating wall
Fig. 4.1
Transfer of heat between two bodies at different temperatures. The two bodies constitute a system that does not
interact with its environment.
PdV work. For a finite heat exchange, the changes in internal energy of the two bodies are
given by:
E
1
=Q
1
E
2
=Q
2
.
(4.1)
Since the system is isolated, its total energy content is constant, so:
E
1
+E
2
=0 (4.2)
from which we conclude what we already knew:
Q
1
=−Q
2
. (4.3)
This is as far as the First Law will take us. It is only from the knowledge that T
1
>T
2
that we
can conclude that Q
1
< 0 and Q
2
> 0. Let us now define a new variable, Z, as follows:
Z =
Q
T
(4.4)
and apply it to the heat transfer process in the isolated system:
Z
isolated system
=
Q
1
T
1
+
Q
2
T
2
=
Q
1
T
1
−
Q
1
T
2
=Q
1
T
2
−T
1
T
2
T
1
> 0. (4.5)
Note very carefully: Q
1
and (T
1
−T
2
) always have opposite signs, regardless of which of
the two bodies is hotter. This is a restatement of the fact that heat flows down a temperature
gradient, and again, a possible way of expressing the Second Law. We can now draw three
conclusions.
(i) Z for heat transfer in an isolated system is always a positive quantity.
(ii) Z = 0 only when T
1
=T
2
, in which case there is no heat transfer.
(iii) Thermal equilibrium in an isolated system is attained when the variable Z attains its
maximum possible value for a given (and fixed) value of the total energy content of
the system.

183 4.2 The entropy postulate
The last point is crucially important in much of what follows, so let me re-phrase it. If the
two bodies are initially at different temperatures, then Z will increase as heat flows from
the hotter to the colder one. Heat will stop flowing when the two temperatures become
equal, at which point we say that the system has attained thermal equilibrium because no
further changes take place with time. At this point Z has attained its maximum possible
value. If the two bodies were initially at the same temperature then the system was already
at equilibrium and the value of Z was already the maximum possible for the total internal
energy content of the system. The fact that heat does not spontaneously flow from a cold
body to a hotter one is called the Clausius statement of the Second Law of Thermodynamics
and is reflected in the fact that Z for an isolated system can never be a negative quantity,
so that Z can never decrease in an isolated system. The italics are important, as forgetting
about this last condition is the source of many misconceptions about the Second Law of
Thermodynamics, especially among pseudo-scientists and other assorted charlatans.
This looks very much like the law that we are looking for, that will allow us to predict the
direction of a spontaneous natural change. We have defined a quantity that always increases
when such a change takes place. There are, however, at least two problems with the variable
Z as we have defined it. In the first place, it may allow us to tell the direction in which heat
flows (which, by the way, we already knew) but it is not at all clear that it will allow us to
predict, for example, whether a chemical reaction will take place, or whether a substance
will melt or crystallize at certain conditions. Second, and more subtly, Z cannot possibly be
a state variable because we have defined it on the basis of a non-equilibrium process: heat
transfer between bodies that differ in temperature by a finite amount is not a quasi-static
process (Section 1.4.2). In the next section we see that with just some minor tweaking we
can define a state function that allows for completely general predictions about the direction
of spontaneous natural processes.
4.2 The entropy postulate and the Second Law of Thermodynamics
Presenting the Second Law of Thermodynamics is the hardest part of any thermodynamics
course. It may seem remarkable that this is the case if the only thing that it does is to codify
everyday experience, such as the fact that your coffee will become cold if you don’t drink it
soon enough. It may even seem that conservation of energy is more removed from intuition
than this. The problem is that the direction of heat flow is just one aspect of the Second
Law, and we seek a statement, and the mathematical law that goes with it, that is completely
general. There are several approaches to accomplishing this. The one that came historically
first relies on thought experiments and theorems about thermodynamic cycles and heat
engines, going back to experimental observations by Carnot and Clausius in the first half of
the nineteenth century, and Kelvin’s work a bit later. I will discuss some of this material in
order to complete the discussion of convection in Chapter 3, but I will not follow this path
in order to introduce the Second Law. The primary reason for eschewing this approach is
that, at some point, one always comes up against postulates or conclusions that appear to
be arbitrary or concocted (although they are not). A better approach, in my view, is to state
our postulates at the very beginning and accept their validity later, on the basis of how well
the mathematical structure that we build from these postulates agrees with reality. In the
words of Callen (1985, p. 27):

184 The Second Law of Thermodynamics
“We...formulate ...a set of postulates depending upon a posteriori rather than a priori
justification. These postulates are, in fact, the most natural guesses that we might make”
This is the spirit of what follows, even though the treatment is much simplified relative to
those of Callen (1985) or Guggenheim (1967).
Drawing from our example in Section 4.1, we define an extensive variable called entropy
and symbolized by S, by means of the following function:
dS =
dQ
rev
T
. (4.6)
The meaning of dQ
rev
is that it is an infinitesimal amount of heat that is transferred
reversibly, which means that no energy dissipation takes place, and that the transforma-
tion takes place between equilibrium states (it is “quasi-static”). The problem is that this
definition of entropy is perfectly circular, because in order to define dissipation (or lack
thereof) we need to know what entropy is, or at least how to measure it. But this is the key:
I am not telling you what entropy is, only how to calculate it. We still have to deal with the
circularity, or at least incompleteness, of (4.6), so we make the following entropy postulate
(Callen’s “most natural guess”):
A process in an isolated system takes place spontaneously only if it causes the entropy
of the isolated system to increase. Equilibrium is attained when the entropy takes the
maximum possible value for the system’s energy content (which is constant in an isolated
system).
This postulate can be motivated by the discussion in Section 4.1, but now we are not making
any mention of heat exchange between different parts of the system. Our postulate is that
entropy increases in any isolated system that changes towards equilibrium (i.e. that under-
goes a spontaneous change), regardless of what the process that leads to equilibrium is (heat
flow, diffusion, chemical reactions, phase transitions, etc.). We express this mathematically
as follows:
dS
isolated system
≥0. (4.7)
We also state that: (i) entropy is a state function, meaning that its value at equilibrium is
fully defined by the state of the system (Section 1.5), (ii) that entropy is additive, i.e. that
it is an extensive property, and (iii) that it is a continuous and monotonically increasing
function of internal energy, E. All of these statements may sound like postulates, but they
can actually be formally demonstrated from (4.6) (see for example Callen, 1985).
At this point it is necessary to address the issue of the “entropy of the universe”. By defini-
tion, the observable universe is an isolated system, so its entropy is constantly increasing as
natural processes unfold. Sometimes, when applying the Second Law to a specific problem,
one analyzes whether or not the entropy of the universe increases, so as to decide whether
or not the process under scrutiny will take place. What we mean with this phrase (which I
will try not to use) is that we are considering the entropy change in a system that is large
enough to include all of the energy and matter exchanges that we are interested in, so that,
as far as our problem is concerned, this system does not interact with anything outside of
it. Commonly we do not have to get anywhere near the edge of the observable universe,
though.

185 4.3 The First Law of Thermodynamics revisited
Worked Example 4.1 Entropy of melting
When a substance melts it absorbs heat. Therefore, by (4.6) its entropy must increase.
Consider melting of water ice at a constant pressure of 1 bar and T = 273 K. The heat
absorbed by melting of ice at constant pressure is the enthalpy of melting, H
melting
≈
6 kJ mol
−1
. The (finite) increase in entropy that accompanies melting, called the entropy
of melting, S
melting
, is therefore given by:
S
melting
=
H
melting
T
melting
≈22JK
−1
mol
−1
. (4.8)
Note that the units of entropy are the same as those of heat capacity. When water crystallizes
it gives off the same amount of heat as it absorbs during melting, so that H
crystallization
=
−H
melting
, and thus S
crystallization
=−S
melting
≈−22JK
−1
mol
−1
. Now, since the
entropy of crystallization is negative, doesn’t the freezing of water violate the Second Law
of Thermodynamics? Of course not. Equation (4.7) applies to an isolated system. Freezing
of water cannot be an isolated system by itself, since the enthalpy of crystallization must be
absorbed by some other body. The temperature of the absorbing body must be lower than the
freezing temperature, because otherwise heat would not flow and water would not freeze.
By the First Law the heat absorbed by this body must be the same as the heat liberated by
the water, but because its temperature is lower, by (4.6) it follows that its entropy increase
is greater than the entropy decrease of freezing water. We can arrange for the freezing water
and the heat absorbing body to conform to an isolated system, whose entropy increases as
ice melts. But what if the temperature of the freezing water and of the absorbing body are
the same? Then S for the isolated system vanishes, which means that the system is at
equilibrium. In such an ideal system water at its freezing temperature never freezes, and ice
at its melting temperature never melts.
4.3 The First Law of Thermodynamics revisited
When we write the First Law as in (1.55):
dE =dQ −dW (4.9)
we make no requirements on the kind of process involved. Equation (4.9) is always true,
regardless of whether or not the process that it describes is reversible, or, equivalently,
of whether or not energy dissipation occurs. Energy conservation cannot be circumvented
under any circumstances. We have implicitly used the generality of (4.9) in many of our
derivations in Chapters 2 and 3 which describe transformations that are dissipative, or
irreversible. For instance, storage of thermal energy in planetary interiors by dissipation of
mechanical, electrical or nuclear energy. As we discussed in Section 1.9, dQ and dW do
not stand for differentials of functions, and for this reason they are often called “inexact”
differentials. Equation (4.9) assures us, however, that their difference is the differential of
a state function. Let us see what happens then, when we write the First Law as follows:
dE =dQ −PdV . (4.10)

186 The Second Law of Thermodynamics
Because E, P and V are all state functions, dQ in this case must be the differential of some
function that takes on a single well-defined value for each state of the system. This is only
possible if (4.10) applies only to transformations between equilibrium states. If this is the
case then we can use (4.6) to make the substitution:
dQ =TdS (4.11)
from which we get the following expression for the First Law, applicable only to
transformations between equilibrium states:
dE =TdS −PdV . (4.12)
This innocent-looking equation, which combines the First and Second Laws, has several
important consequences. We will examine the most momentous ones in Section 4.8. For
now, we note that it is written only in terms of state variables, i.e. quantities that are well
defined in any equilibrium state. We can therefore integrate equation (4.12) in order to
calculate the change in entropy between two arbitrary equilibrium states. We can apply the
same arguments to the First Law written in terms of enthalpy (equation (3.27)):
dH = TdS +VdP . (4.13)
The following two identities follow immediately from equation (4.12):
∂E
∂S
V
=T (4.14)
and:
∂E
∂V
S
=−P . (4.15)
These equations are the thermodynamic definitions of temperature and pressure. They allow
a number of algebraic manipulations that are crucial in the formal development of the
conditions of chemical equilibrium. We shall have much more to say about this, beginning
in Section 4.8.
4.4 Entropy generation and energy dissipation
We will use an example to gain some insight into the nature of entropy, and more specifically
into the relationship between entropy generation and energy dissipation. Consider a system
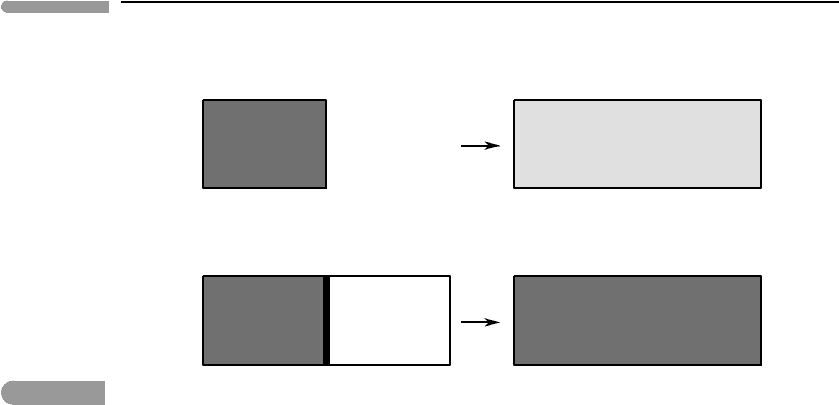
undergoing two different types of adiabatic expansion (Fig. 4.2). In case (a) the system
undergoes a quasi-static expansion from an initial volume V
i
to a final volume V
f
. If the
system is a gas then we recall from Section 1.4.2 that this means that the expansion is
slow enough that molecular velocities preserve an equilibrium statistical distribution, but
equivalent statements can be made for a system in any aggregation state (e.g. distribution
of vibrational frequencies in a solid). During the quasi-static transformation the system
expands against an external pressure that is always infinitesimally close to its own pressure,
and that decreases infinitesimally slowly. In case (b) the system undergoes the same change
in volume as a result of a free expansion. This means that the substance of interest, for
187 4.4 Entropy generation and energy dissipation
(b) Free expansion
(a) Quasi-static expansion
V
i
V
i
V
f
V
f
V
f
-V
i
T
f
<T
i
T
f
=T
i
Fig. 4.2
(a) Quasi-static expansion of an ideal gas performing work on its environment. (b) Free expansion of an ideal gas into
a vacuum. Shading represents temperature.
example a gas, initially occupies a volume V
i
, and the rest of the system’s volume, V
f
−V
i
,
is empty and separated from the volume filled with gas by a partition. The partition is
removed and the gas expands to fill the entire volume V
f
. The transformation is not quasi-
static, but we are free to allow enough time to elapse after the expansion, such that the
system eventually reaches thermal equilibrium, in the sense of Section 1.4.2.
Because both transformations are adiabatic, we have, for both cases:
dQ =dE +dW =0. (4.16)
During the quasi-static transformation (a), the system expands against an external pressure
equal to its own pressure, so dW = PdV :
dE
quasi-static
+PdV =0 (4.17)
and, substituting (4.12):
TdS
quasi-static
−PdV +PdV = 0 (4.18)
or:
dS
quasi-static
=0. (4.19)
Thus, the quasi-static adiabatic expansion that we described is also isentropic. We may ask,
if there is no entropy change during a quasi-static expansion, then why does the expansion
occur at all? Wouldn’t that imply that the system is at equilibrium, and that a spontaneous
compression, or better yet, no change at all, are as likely, or unlikely, as a spontaneous
expansion? There are several answers to this question, but they all boil down to the fact
that the description that I gave of the system is incomplete, and that the system as described
is not isolated. Expansion occurs within a larger isolated system in which entropy must
increase. The condition dS = 0 applies only to the system expanding quasi-statically. But
in order for it to be possible for the system to expand and perform work against an external
force the energy must have been previously stored in the system as internal energy, for
example by heating the system and causing its temperature to rise. During the heating stage
