Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

138 Energy transfer processes in planetary bodies

Lord Kelvin obtained his estimate for the age of the Earth by solving equation (3.22) for t:

t =

πκ



(

−T

)



. (3.23)

Box 3.2

Summary of terrestrial heat ﬂow

Throughout this chapter we will use terrestrial heat ﬂow values in numerical examples, but the values

appropriate to each example are not necessarily the same. This brief review, based on data discussed by

Turcotte and Schubert (2002) and Davies (1999), which are in broad agreement with one another, explains

the reasons for the various choices.

The total terrestrial heat output is approximately 4.43 × 10

W. Divided by the surface area of the

Earth (5.1 ×10

), this yields an average terrestrial heat ﬂux of ≈87 mW m

−2

. This total includes: (i)

heat lost from the deep planetary interior by advection (mostly by sea ﬂoor spreading, which is the surface

expression of mantle convection, plus a small but not negligible contribution from mantle plumes), (ii) heat

lost from the deep planetary interior by diffusion across the continental lithosphere, and (iii) heat generated

by radioactive decay in the continental crust. Table 10.1 in Davies (1999) summarizes the magnitude of

these various contributions. For our purposes, the important concept is that the total average terrestrial heat

ﬂux of 87 mW m

−2

does not discriminate between different sources, depths of origin or heat transport

mechanisms. This is the correct value to use, for example, if we wish to model terrestrial heat loss as the

product of a single heat transport process that applies indiscriminately to the entire Earth and in which the

source of heat is the same for all parts of the Earth. Kelvin’s diffusive cooling model is an example of this.

If we subtract radioactive heat generation in the crust, we are left with a total heat loss from the Earth’s

deep interior (mantle +core) of ∼3.6 ×10

W. This includes heat ﬂowing from the mantle across both

the oceanic and continental Moho. Divided by the total surface area of the Earth, this yields an average

heat ﬂux from the deep Earth of ∼70 mW m

−2

. This is not, however, the heat that is transported to the

Earth’s surface by mantle convection, as part of this heat is transported to the Moho by diffusion across the

continental lithosphere. Subtracting the contribution from the subcontinental mantle, including continental

shelves, yields a total heat loss across the ocean ﬂoor of ∼3.1 ×10

W. This is the heat that is transported

to the surface by mantle convection (if we ignore radioactive heat generation in the oceanic crust, which is

a very small fraction of this total). Divided by the surface area of ocean ﬂoor, about 3.1 ×10

, it yields

an average oceanic heat ﬂux of 100 mW m

−2

. Perhaps 10–20% of this corresponds to heat transport by

mantle plumes. The rest, 80–90 mW m

−2

, is the heat ﬂux that must be accounted for by the moving-plate

mode of mantle convection, i.e. formation of oceanic lithosphere at spreading centers and destruction of this

lithosphere at subduction zones.

We will discuss mantle convection in other terrestrial planets as well, and in order to do that we need

a rough estimate, or at least a bounding value, for the planet’s heat ﬂux. If we assume that the bulk

compositions and differentiation histories of two planets are the same, then we can tentatively conclude

that the heat outputs per unit mass (see Chapter 2) of the two planets are similar. If the sizes of the planets

are different, however, the surface heat ﬂuxes will not be the same, as surface area scales with the square of

radius and mass with the cube. Calling the two planets 1 and 2, we ﬁnd:

, (3.2.1)

139 3.3 Heat diffusion and cooling of planetary bodies

Box 3.2

Continued

where q is surface heat ﬂux, r radius and ρ density. This formula is strictly applicable only if all of the surface

heat ﬂux comes from an active heat source, such as radioactive decay. If some of the surface heat ﬂux reﬂects

secular cooling, i.e. slow release of internal energy stored early in the planet’s history by processes such as

accretion, differentiation, tidal heating or decay of short-lived radioactive isotopes, then smaller planets with

a larger surface to mass ratio will cool faster and equation (3.2.1) would not be applicable for the present

age of the Solar System. If the planets are not too different in size, however, (3.2.1) may yield a reasonable

estimate. This is the case for Venus and Earth. Using (3.2.1) and the average heat ﬂux from the deep Earth

(70 mW m

−2

) yields an estimate for Venusian mantle heat ﬂux of 63 mW m

−2

. Application of this

relationship to smaller terrestrial planets is more contentious. For Mars we calculate an “Earth analog”

mantle heat ﬂux of ∼30mWm

−2

. In Chapter 2 we saw that geochemical estimates suggest a total Martian

heat ﬂux of 40 mW m

−2

, so that, accounting for upwards enrichment of radioactive isotopes, the mantle

heat ﬂux estimated from (3.2.1) is not altogether unreasonable. For the Moon we get 12 mW m

−2

, which

is about half of the average value obtained from two measurements by Apollo crews. The anomalous lunar

heat ﬂow, if real, could be a fossil of an extreme heating event cause by tidal despinning (Chapter 2).

In addition to the material properties k and κ and the surface heat flux, q

(see Box 3.2),

the solution requires values for the initial temperature of the Earth, T

, and for the sur-

face temperature T

. A nice round number such as 300 K is a reasonable enough value

for the latter, but what about the initial temperature? As we saw in Chapter 2, this is very

poorly constrained, and it was all but unknown in Kelvin’s time. He seems to have cho-

sen a value on the order of 4000 K, on the basis of what little was known at that time on

melting temperatures of rocks. Given the significant uncertainties in initial temperature,

measured geothermal gradients and thermal properties for rocks, Lord Kelvin gave a pos-

sible age range of 25–400 million years. Using the value for mean terrestrial heat flux,

including continents and oceans, of ∼87 mW m

−2

(Box 3.2), typical values for k and κ of

3Wm

−1

and 10

−6

−2

, respectively, and T

–T

= 3700 K we obtain t = 5.18 ×

s ≈ 164 million years, within the range of Kelvin’s results.

Let us now start from the known age of the Earth, 4.56 Ga ≈1.44 × 10

s. If we assume

the same initial temperatures, T

–T

= 3700K,wecalculate a mean present-day surface

heat flux of ∼16.5 mW m

−2

, about one fifth of the observed value. Alternatively, using

the actual heat flux of 87 mW m

−2

, we arrive at an initial temperature of ∼19 800 K for a

conductively cooled Earth of the correct age. On the basis of our results from Chapter 2,

this temperature is unrealistically high, but there is a bigger problem.

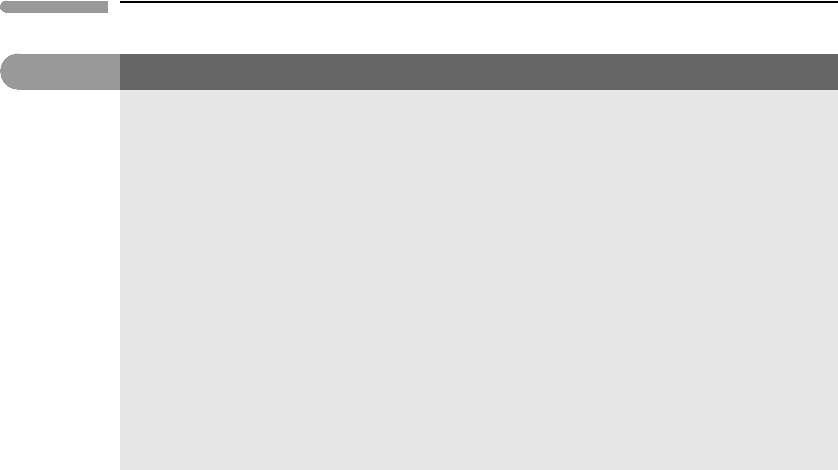
A way of looking at these results is presented in Fig. 3.6 which shows temperature as a

function of depth, calculated with equation (3.17), for the three models discussed above.

Model 1 is a 4.56 Ga Earth with an initial temperature of 4000 K. This we can discard on

the basis of the observed surface heat flux. Model 2 has the same initial temperature but

is 164 million years old, which as we saw yields the correct mean terrestrial heat flux of

87 mW m

−2

. In addition to an erroneous age, this model requires a temperature of 4000 K

at a depth of ∼300 km, which is above the peridotite liquidus. Model 3, which is based on

the correct heat flux (note that dT/dx at the surface coincides with that of model 2) and the

correct age of 4.56 Ga, requires a temperature of 19 000 K, or several times the peridotite

liquidus, at a depth of 1500 km, and is obviously unacceptable on geophysical grounds, as

it requires a present-day molten mantle.

140 Energy transfer processes in planetary bodies

0 5000 10000 15000 2000

2000

1500

1000

500

Temperature (K)

Depth (km)

2 3

Fig. 3.6

Three diffusive thermal proﬁles of the Earth, all incorrect. Models 1 and 3 are for a 4.56 billion year old Earth, with

initial temperatures of 4000 K and ∼20 000 K, respectively. Model 3 yields the correct surface heat ﬂux, as does

model 2, which requires a 164 million year old Earth and a 4000 K initial temperature. Note that if the Earth cooled

diffusively then most of the planet would still be at its initial temperature, regardless of what this temperature was.

Diffusive length and time scales are independent of temperature.

The clue to the failure of the conductive model of terrestrial cooling is that, if the Earth

cools by diffusion, then the source of the heat flow observed at the surface is only a small

fraction of its internal energy content. The heat flow observed at the surface would be

driven by cooling of the thermal boundary layer. For an Earth of the correct age, and even

more so for Lord Kelvin’s age estimate, most of the planet’s interior is located beyond the

characteristic diffusion length, so that much of the Earth’s primordial internal energy would

remain stored and incapable of contributing to the planet’s surface heat flow at the present

epoch of the Solar System. The importance of Lord Kelvin’s mistake is that it shows that

conductive cooling of an Earth with no active heat sources fails to explain the observed

thermal structure of the planet (which, it must be stressed in his defense, was not known

in his time). There are two possible solutions. One, terrestrial heat flow may include a

contribution from an active heat source in addition to heat flow derived from cooling of the

thermal boundary layer. As we saw in Chapter 2, the only feasible heat source active today

is radioactive decay. Alternatively, the planet may have a thin conductive outer layer, below

which another heat transfer process is active, that is capable of tapping internal energy

from the large proportion of the Earth that lies beyond the diffusive boundary layer, and of

delivering this heat to the base of the conductive skin.

3.3.2 Can the conductive model for the Earth be saved?

Let us examine the contribution of radioactive heat production to a conductively cooling

Earth. We will assume that the entire terrestrial budget of long-lived radioactive isotopes

141 3.4 Convection as a heat engine

is concentrated in the thermal boundary layer. This is justified on two grounds. First, it

is the best case scenario, for radioactive heating originating beyond the thermal boundary

layer cannot contribute to heat flow across the surface. Second, the assumption is sound on

geochemical grounds, because all long-lived isotopes are incompatible elements that tend

to migrate to the outer layers of the Earth.

If α is the present-day bulk Earth rate of radioactive heat production per unit mass, M

is the Earth’s mass and R its radius, then the heat flux derived from radioactive decay

is (αM)/(4π R

). Using the value of α from Fig. 2.20, ∼2.7 × 10

−12

Wkg

−1

, we get a

maximum contribution from present-day radioactive decay of 31 mW m

−2

. Given a total

terrestrial heat flux of 87 mW m

−2

, it is necessary to derive 56 mW m

−2

from diffusive

cooling. From equation (3.22) we calculate that the initial temperature of the Earth required

to yield this heat flux is ∼12 200 K, and this primordial temperature would still exist today

at a depth of ∼1500 km (see Fig. 3.6), which we know is not possible (it is still several

times the peridotite liquidus).

The Earth is certainly still today losing internal energy from an initial hotter state. The fact

that the core has not yet completely solidified is one indication of this. Diffusion, however,

cannot be the heat transfer process responsible for extracting heat from the Earth’s deep

interior. The only viable alternative is convection, as silicates are opaque to infrared radiation

(Chapter 13).

We should look at Lord Kelvin’s mistake in a different light. Unknown to him, his

greatest contribution to the Earth Sciences was to demonstrate that convection must be

occurring in the interior of our planet. In my view, the realization that this is the case, and

the ensuing quantitative understanding of convection in planetary mantles in general, is

as pivotal to planetary sciences as the replacement of the Ptolemaic view of the cosmos

with the Copernican one. One could say that geology before the understanding of mantle

convection was what Aristotelian mechanics is to Newtonian mechanics.

3.4 Convection as a heat engine

Heat engines are thermodynamic cycles that convert thermal energy to mechanical energy

continuously and indefinitely, as long as there is a net input of heat (this is the First Law

of Thermodynamics), and as long as there are two thermal reservoirs at different temper-

atures that the engine can exchange heat with (this is mandated by the Second Law of

Thermodynamics, which we will study in Chapter 4). The heat engine extracts heat from

the high-temperature reservoir and releases heat to the low-temperature reservoir. If the dif-

ference between heat absorbed at high temperature and heat released at low temperature is

greater than zero then there is the capability of performing work. We see from this descrip-

tion that a heat engine also acts as a heat transport mechanism. Convection fulfills this dual

role in planetary bodies. On the one hand, convection is the heat engine that underlies such

diverse processes as plate tectonics, mountain building, planetary dynamos, and hurricanes.

Convection is also the predominant heat transport process in active planetary mantles and

cores, as well as in planetary atmospheres and oceans.

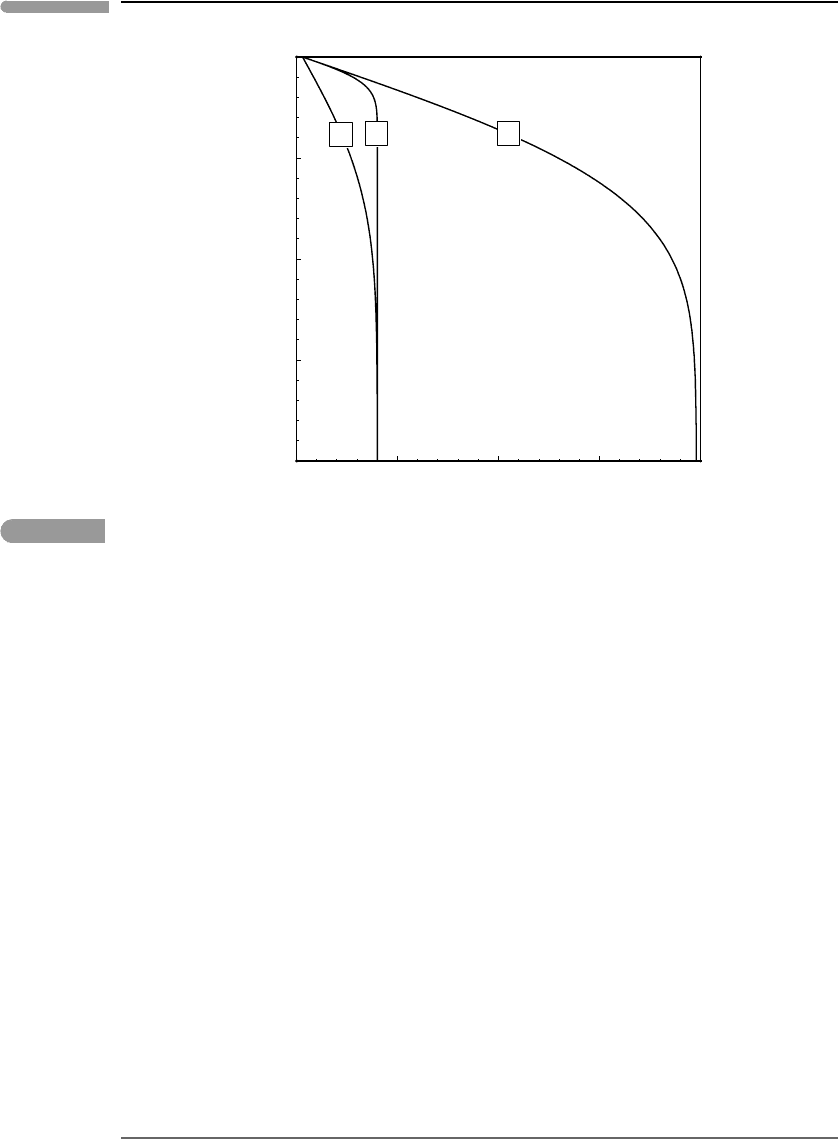
We will construct a “toy model” of convection in a planetary mantle. By “toy model”

I mean that I will make a number of simplifying assumptions in order to extract some of

the physics of the process. First, it is customary to refer to the convecting material as a

fluid, even if, as in the case of planetary mantles, the material is a crystalline solid that is

142 Energy transfer processes in planetary bodies

adiabat

Fig. 3.7

Toy model of planetary convection. A parcel of material absorbs heat isobarically along the bottom boundary of the

convective layer, so that its temperature increases from A to B. It then rises adiabatically from B to C, loses heat

isobarically from C to D and sinks adiabatically from D to A, completing the cycle.

able to flow at rates of cm to m per year by a combination of microscopic and macroscopic

creep mechanisms (see Poirier, 1985). Convection occurs when the temperature difference

across a fluid layer is such that, given the magnitudes of material properties of the fluid

such as thermal diffusivity, coefficient of thermal expansion and viscosity, the rate of heat

transfer by advection exceeds the rate of heat transfer by diffusion. The fluid layer (Fig.

3.7) absorbs heat across its bottom boundary and releases heat across its top. In our toy

model we assume that pressure is constant along both boundaries. This is physically rea-

sonable for terrestrial mantle convection. The top of the convecting mantle corresponds

to the surface of the Earth (more precisely, the ocean floor). The bottom corresponds to

the core–mantle boundary, where the pressure is determined by the lithostatic load of the

overlying mantle so that it is essentially constant. Significant lateral temperature variations

exist along both boundaries. As the mantle releases heat through the planet’s surface, it

cools from asthenospheric temperature at mid-ocean ridges to atmospheric temperature at

subduction zones. We are less certain about what happens at the bottom boundary, but a

reasonable physical model is that cold downwelling mantle hits the core–mantle boundary,

moves laterally and its temperature rises as it absorbs heat from the core (see Fig. 3.7). This

toy model of convection assumes that heat exchange occurs only at the bottom and top of the

convective layer, and that there are neither heat sources nor heat sinks within the convect-

ing fluid. The latter is seldom the case in real planetary systems. For example, radioactive

heat is generated in planetary mantles (and perhaps cores as well), frictional dissipation of

mechanical energy takes place in planetary cores, mantles and atmospheres, ohmic dissi-

pation is always part of planetary dynamos, and phase changes of condensable species are

huge heat sources and sinks in planetary atmospheres (H

O in Earth, hydrocarbons in Titan,

in Mars).

143 3.4 Convection as a heat engine

It is the nature of convection that it must transfer heat faster than diffusion. This is so

because convection is driven by buoyancy forces, which in thermal convection arise from

temperature differences. Buoyancy can be maintained only if temperature contrasts between

different parcels of fluid can be maintained. The rate of change of the thermodynamic state of

a parcel of fluid not located at the heat exchange boundaries must therefore be much faster

than the rate at which heat can be exchanged by diffusion with neighboring parcels. This

means that the interior of the convective layer is adiabatic (Fig. 3.7). Planetary convective

systems may differ in some important aspects, though. For example, in contrast to the

model in Fig. 3.7 in which both heat absorption and heat loss are isobaric, hurricanes are

convective systems in which both heat transfer boundaries are approximately isothermal.

The basic structure of two heat-transfer boundaries linked by an adiabatic interior is always

present, however.

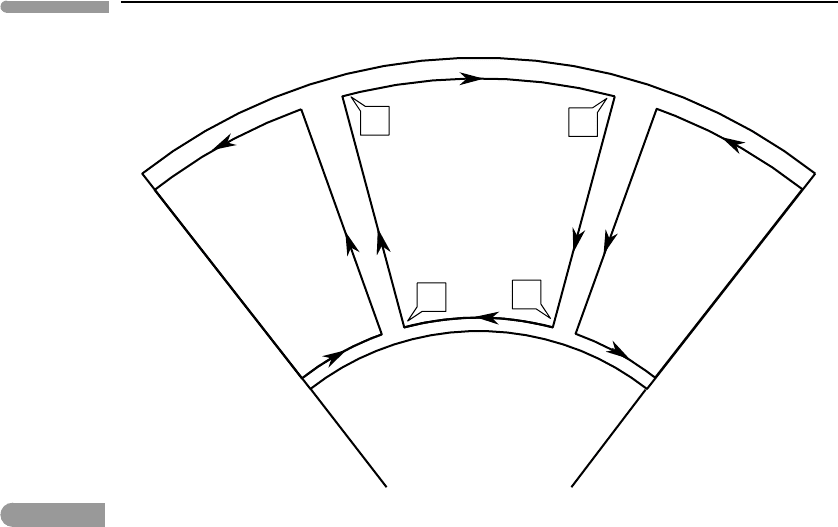
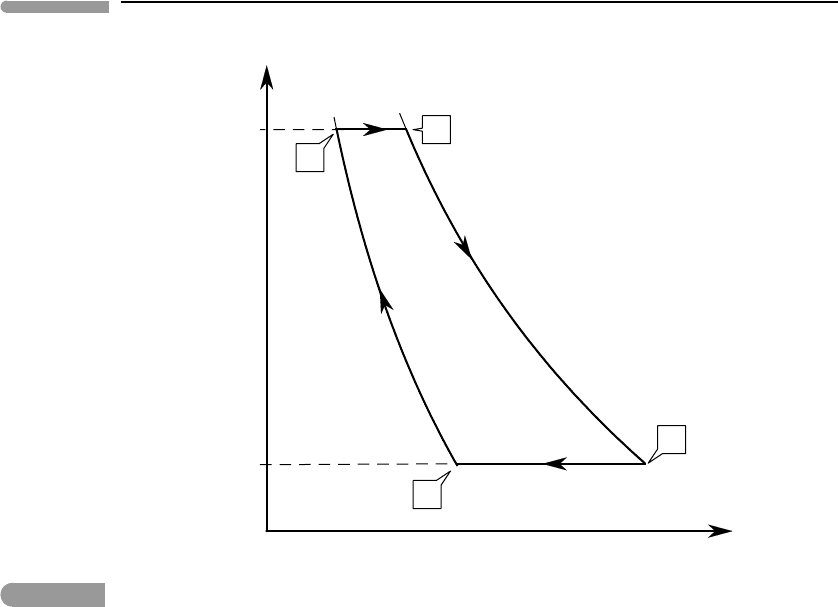
The convective overturn depicted in Fig. 3.7 maps as a four-leg cycle on a pressure–

temperature diagram, shown in Fig. 3.8. A parcel of material located at the bottom of the

convective cell, at point A, absorbs heat at constant pressure P

.As its temperature increases

from T

to T

the material expands until it eventually becomes buoyant at B. It then rises

and expands adiabatically, from P

to P

.Adiabatic expansion causes its temperature to drop

from T

to T

.AtC the parcel has reached the top of the convective layer and begins to

lose heat. It cools down isobarically from T

to T

and contracts, until at D the density has

increased sufficiently that it sinks and compresses adiabatically. Its temperature increases

in response to adiabatic compression until it reaches the bottom boundary at A. The function

T = T(P)along an adiabatic path such as BC or DA is called the adiabat and is discussed

adiabat

Fig. 3.8

Pressure–temperature diagram for the planetary convection model shown in Fig. 3.7.

144 Energy transfer processes in planetary bodies

adiabat

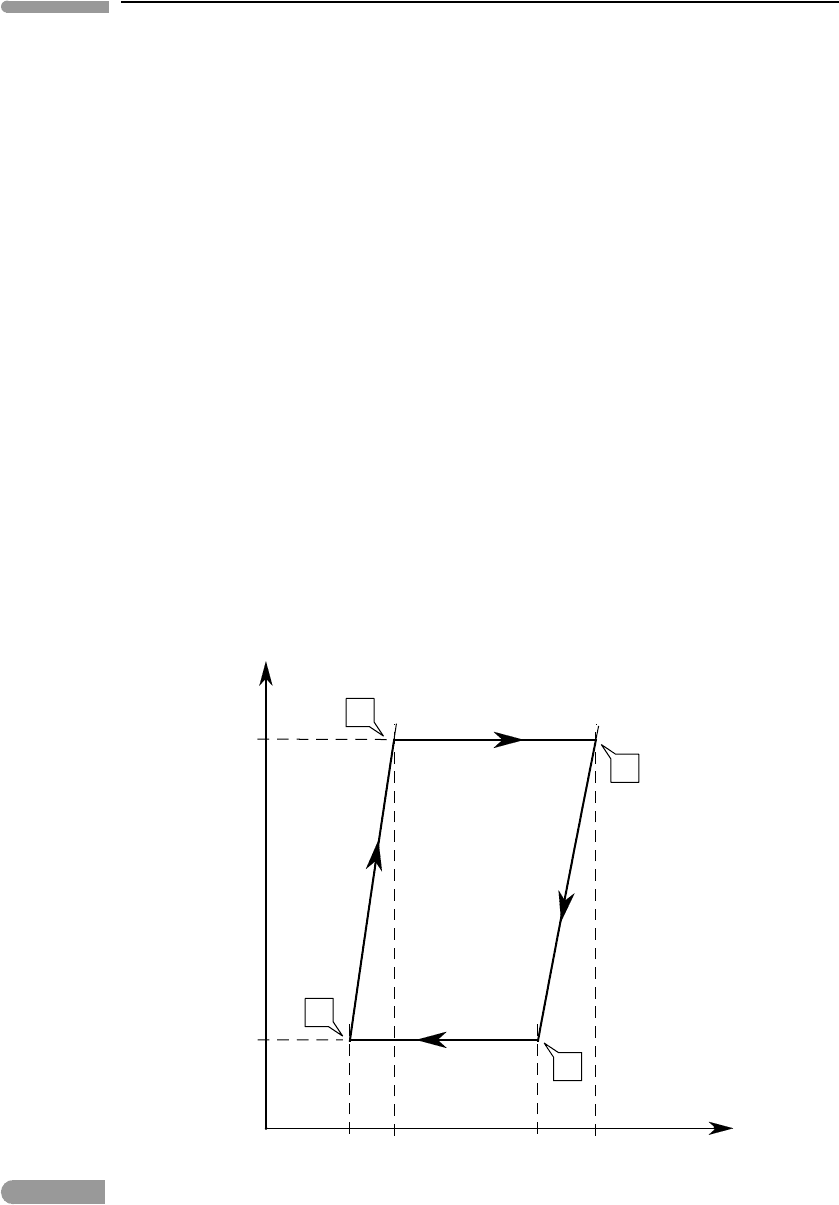
Fig. 3.9

Pressure–volume diagram for the planetary convection model shown in Fig. 3.7. The area bound by the four curves is

the net work delivered by the cycle. In a planetary mantle most of this work is dissipated by viscous ﬂow, and a very

small fraction is transformed to other types of mechanical energy such as potential energy (topography) and elastic

energy in the lithosphere.

fully in the next section, as it is a key element in the quantitative analysis of convection and

in the study of many planetary processes.

Because the integral of a function P =P(V ) with respect to V represents mechanical work

(Section 1.4.1) mapping the convection cycle onto a pressure-volume diagram allows us to

explore the energetic aspects of the process. The adiabats are logarithmic curves on a P–V

diagram (see end-of-chapter problems) so that the convection cycle maps onto the P–V plane

as shown in Fig. 3.9. The net work performed by the thermodynamic cycle is represented

by the area bound by the four legs of the cycle. The heat absorbed at high pressure (from A

to B) places the fluid on a hotter adiabat, which delivers work during expansion. The fluid

must then return to the colder adiabat, by losing heat from C to D, and then work must be

performed on the system in order to compress it along the colder adiabat, from D to A. The

integral of dE around a full cycle must vanish, because internal energy is a state variable

(Section 1.9). Therefore, applying the First Law of Thermodynamics to convection and

using the symbol



which means integration along a closed path, we see that:



dE =



dQ −



dW =0 (3.24)

or:



dQ =



dW. (3.25)

145 3.5 Planetary adiabats

The net work performed by a thermodynamic cycle equals the net amount of heat absorbed

by the cycle. In our toy convection model, this equals the heat absorbed along the high-

temperature isobaric path (from A to B), minus the heat released along the low-temperature

isobaric path (from C to D). The amount of work varies directly with the pressure difference

across the convecting layer (i.e. the length of the adiabats) and with the amount of heat that

can be extracted from the high-temperature source or delivered to the low-temperature sink

(i.e. the length of the two heat-exchange paths). Convective overturn is driven by buoy-

ancy, i.e. by gravitational forces, but what makes it possible is the temperature difference

between the ascending adiabat (B to C) and the descending adiabat (D to A). A temperature

difference between adiabatic paths can only be maintained if there is heat exchange at both

boundaries (see Fig. 3.9), or, equivalently, if there are at least two non-adiabatic legs in the

cycle. Either of them, or both, can exert the dominant control on convection. For instance,

the chief driving force for terrestrial mantle convection is cooling at the upper boundary and

formation of the negatively buoyant and mobile lithosphere. Terrestrial mantle convection

is largely controlled by the length of the cooling path CD in Fig. 3.9, i.e. by the temperature

difference T

–T

(Fig. 3.8).

The convection heat engine absorbs heat at the high-temperature boundary and releases

heat at the low-temperature one, thus playing the part of a heat transport mechanism. It

can keep operating only as long as it is not outpaced by heat diffusion. As a planet cools

down the four legs of the cycle depicted in Fig. 3.9 approach one another and geological

activity declines. At some point the material becomes too stiff to be able to convect and the

planetary heat engine seizes. The planet may still contain a substantial amount of thermal

energy but this is diffused to the surface and radiated to space without performing work.

The Moon is an example of a planetary body in this evolutionary stage.

In real convection there are important additional considerations.Afraction of the mechan-

ical energy that convection delivers at the expense of the planet’s thermal energy is always

dissipated. If the convective layer consists of very viscous and electrically insulating mate-

rial, such as the Earth’s mantle, virtually all of the mechanical energy is dissipated by

friction and returned to the mantle as heat. The remainder, a very small fraction of the total

energy flow, is transferred to the planet’s lithosphere, where it is stored as elastic energy and

gravitational potential energy (topography; e.g. Worked Example 1.1). In a convective layer

that is electrically conductive some of the mechanical energy appears as electric currents,

which are dissipated by ohmic heating while sustaining the planet’s magnetic field (Section

1.8.3). In planetary atmospheres, because of their low viscosity, there may be significant

conversion of heat to kinetic energy of wind, that is eventually dissipated by friction, both

within the atmosphere itself and between the atmosphere and the planet’s liquid or solid

surface (wind turbines tap a small fraction of this kinetic energy).

3.5 Planetary adiabats

The work performed by an adiabatic process must be balanced by a change in internal

energy. Therefore, a function must exist that relates temperature to pressure anywhere

along an adiabatic path. Such a function is called the adiabat and allows us, for instance, to

calculate temperature as a function of pressure (or depth) in an actively convecting mantle,

or atmospheric temperature as a function of elevation in a convecting atmospheric layer

(the troposphere). If we know temperature and pressure at one point on the adiabat then we

146 Energy transfer processes in planetary bodies

can calculate the temperature at any other pressure. For instance, we can see by reference

to Fig. 3.8 that if a planet has a convective interior, then we can calculate the temperature

at depth in the planet from temperature measurements at some reference level close to its

surface.

We seek a function T =T (P ) along an adiabatic path. To begin, we re-state the First Law

of Thermodynamics in terms of enthalpy, because enthalpy allows us to write equations in

terms of the variables P and T more compactly than internal energy. From the definition of

enthalpy (equation (1.59)), an infinitesimal change in H is given by:

dH = dE +PdV +VdP (3.26)

substituting into the equation for the First Law (equation (1.56)) and simplifying:

dH = dQ +VdP. (3.27)

Along an adiabatic path dQ = 0, so for the adiabat equation (3.27) becomes:

dH = VdP. (3.28)

If pressure and temperature are the variables of interest we must express dH in terms of

infinitesimal T and P increments. This is given by (see equation (1.3.3), Box 1.3):

dH =



∂H

∂T



dT +



∂H

∂P



dP = C

dT +



∂H

∂P



dP. (3.29)

Substituting in equation (3.28) and rearranging:

dT =



V −



∂H

∂P





dP. (3.30)

To simplify this equation further we must express (∂H/∂P)

in terms of some combination

of the state variables: P , V , T and the material properties: K

, α and C

(Section 1.11).

In order to derive the required expression we must use both the first and second laws

of thermodynamics, so we will defer a full discussion until Chapter 4. The derivation is

presented in detail in Appendix 2, where it is shown that:



∂H

∂P



(

1 −αT

)

. (3.31)

Substituting in equation (3.30) we obtain the equation for the adiabat:

αV

dP. (3.32)

In the derivation of equation (3.32) we have tacitly assumed that the adiabatic transfor-

mation is also reversible (Section 1.4.2 and Chapter 4). This happened when in equations

(3.26) and (3.27) we equated PdV to the work performed by the adiabatic expansion, which

is only true if there is no energy dissipation and therefore, as we shall see in Chapter 4,no

entropy generation. Although it is certainly an adiabat, equation (3.32) is more accurately

called an isentrope, as there are adiabatic transformations that are not isentropic (Chapter

4). It is customary in planetary sciences, however, to call (3.32) “the adiabat” and I will

generally follow this custom. This commonly presents no problems, but in cases in which

147 3.5 Planetary adiabats

it is necessary to examine the constant entropy assumption more rigorously we will do so

(Chapter 10).

We are often interested in how temperature varies with depth in a planetary interior, or

elevation in the atmosphere. From the chain rule of partial differentiation:

. (3.33)

The pressure gradient inside a planet is given by the condition of hydrostatic equilibrium

(equation (2.34)), but whereas r in equation (2.34) is measured from the center of the planet

outwards, y is defined as positive downwards, so we have:

=gρ (3.34)

and, using (3.32) and (3.33):

αgT

, (3.35)

where we recall that c

= C

/(Vρ) is the specific heat at constant pressure (= constant

pressure heat capacity per unit mass).

Because we have made no assumptions regarding the equation of state of the material

that undergoes the adiabatic transformation, equations (3.32) and (3.35) are completely

general. In order to integrate them, however, it is necessary to know the equation of state

of the material of interest, so as to express α, V and C

as functions of P and T.Itmay

also be necessary to consider changes in g with depth. We can nevertheless get an order of

magnitude estimate of the adiabatic thermal gradient in the Earth’s upper mantle by using

characteristic values for forsterite. These are: α ≈ 3 ×10

−5

−1

, v ≈ 3 × 10

−4

−1

and c

≈1200 J K

−1

. Note that although (3.32) is written in terms of molar properties,

it is also valid if we express volume and heat capacity as specific properties, as the unit

conversions cancel out. Taking g = 9.8ms

−2

and a characteristic upper mantle temperature

T = 1700 K, we get an adiabatic gradient for the asthenosphere of ∼0.4Kkm

−1

or ∼1.3

K kbar

−1

. Temperature increases with depth, and the coefficient of thermal expansion

and the heat capacity are both functions of temperature and pressure (Chapter 8). The

adiabatic temperature gradient decreases at greater depths. It is always much smaller than

the temperature gradient in the lithosphere, however, in which heat transfer is by diffusion.

For example, the temperature difference across the oceanic lithosphere is of the order of

1400 K. With a lithospheric thickness of 100 km, this yields, assuming no radioactive heat

generation, a mean diffusive temperature gradient of 14 K km

−1

Worked Example 3.1 Atmospheric lapse rate

Equation (3.35) can be used to calculate how temperature varies with elevation in the

atmosphere, provided we are careful about some points. First and foremost, the thermal

gradient will be adiabatic only in those layers in which the atmosphere is convecting. This

is true, for example, for the terrestrial troposphere, up to ∼10 km above sea level, but not

at higher elevations. Second, even in the convective troposphere the adiabatic condition