Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

58 Energy in planetary processes

Choosing a surface perpendicular to one of the three axes that define the degrees of freedom

does not cause any loss of generality, because we can choose the orientation of the axes

(Fig. 1.11) any way we want, as long as they are mutually perpendicular. In other words,

pressure is isotropic.

If the molar volume of the gas is V then opposite walls are separated by a distance of

order V

1/3

and the time between consecutive collisions is (2V

1/3

)/u, because the particle

must move to the opposite wall and back. The rate of change of momentum of a particle

when it collides with a wall, i.e. the force exerted by a particle on a wall, is then given by:

2mu

1/3

−1

1/3

. (1.107)

The total pressure must equal the average force per particle, times the number of particles,

divided by the surface area of the wall. In order to account for the average force per particle

we must use the mean-square speed, u

, because we are averaging rates of change of

momentum, which scale as the square of speed (equation (1.107)). The surface area of the

wall is of order V

2/3

, so that the pressure is given by:

P = N

mu



1/3

2/3

Nmu



(1.108)

hence:

PV = Nmu

. (1.109)

Using the ideal gas EOS, PV = RT, we obtain:

T =

Nmu



mu



, (1.110)

where k

=R/N is the gas constant per molecule, known as Boltzmann’s constant. We can

also write equation (1.110) as:

T =

mu

. (1.111)

This equation relates the temperature of the gas to the average kinetic energy of the particles

along each degree of freedom. It allows us to calculate a characteristic value for molecular

speeds, the root-mean-square speed (RMS) of the molecules, c



=(3u

)

. Molecular

speeds were first calculated in this fashion by James Joule in the mid nineteenth century. The

root-mean-square speed is not the same as the most probable molecular speed mentioned in

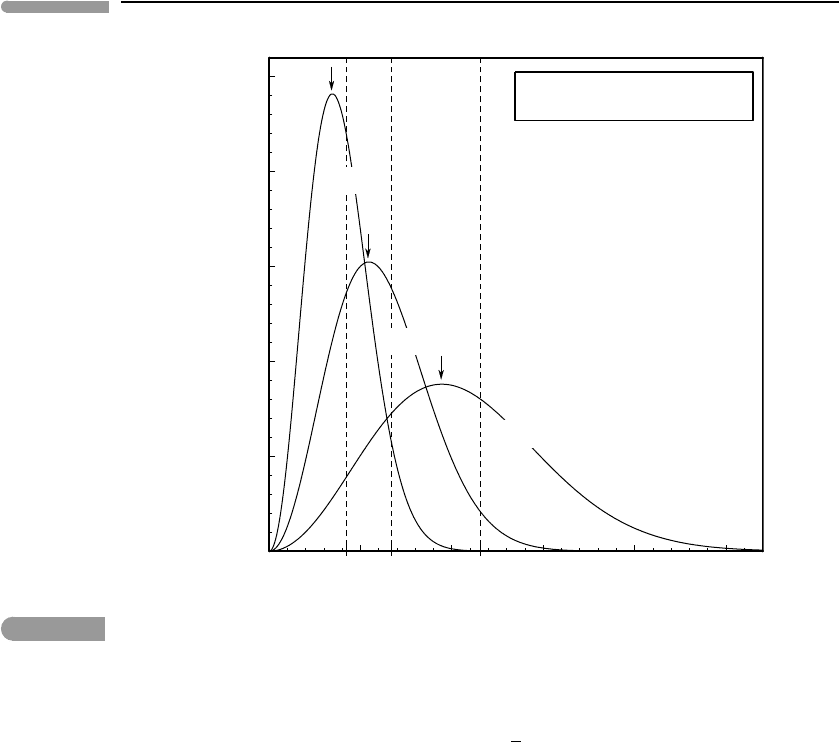
Section 1.4.2. The relationship between the two quantities is shown in Fig. 1.12. The RMS

molecular speed is always greater than the most probable speed, reflecting the long tail on

the high speed end of the Maxwell–Boltzmann distribution. This long tail, which implies

that there always are a significant number of molecules that are moving with speeds that

are much faster (by a factor of 2–3) than the most probable value, plays an important role

in the escape of light gas species from planetary atmospheres. This is especially the case

for escape of hydrogen from primordial planetary atmospheres, and will be discussed in

Chapter 13.

Equations (1.105) and (1.111) each relates a microscopic variable (E or T) to the kinetic

energyof the particles.We can substitute one equation into the other to arrive at an expression

59 1.14 Internal energy

0 500

1000

1500 2000

2500

0.001

0.002

Molecular speed (ms

–1

)

Probability density

Distribution of molecular speeds

and RMS speeds for N

200 K

500 K

1500 K

Fig. 1.12

Most probable speed (arrows) and RMS speed (dashed lines) for N

at 200, 500 and 1500 K.

for the molar internal energy of a monatomic ideal gas as a function of absolute temperature:

monatomic

RT . (1.112)

This equation shows that the internal energy of an ideal gas is a function of temperature

only, so that for any ideal gas (∂E/∂P )

= (∂E/∂V )

= 0. For real substances these

derivatives do not vanish. They vanish for ideal gases only because of our assumptions:

non-interacting, perfectly elastic particles with no volume. Also, since C

= (∂E/∂T )

we get C

=3/2 R for a monatomic ideal gas.

Note what we have done here: from a simple hypothesis about the microscopic nature of

an ideal gas and the principle of equipartition of energy we have derived a mathematical

expression for the relationship between two macroscopic variables. The validity of our

assumptions can then be tested by comparing predicted internal energies of ideal gases

with measurements for real gases at conditions such that their behavior approaches that of

ideal gases. We will do this in the next section, using C

rather than E, because C

can be

obtained from direct experimental measurements whereas E cannot.

We could have derived these same results from statistical mechanics, with one crucial

difference. In our derivation using only kinetic theory we had to use the ideal gas EOS

(in equation (1.110)), which arises from macroscopic observations. Statistical mechanics

allows us to do away with this last piece of macroscopic physics – we can derive both

the expression for internal energy (equation (1.112)) and the ideal gas EOS solely from

the (microscopic) partition function. The importance of this is that the same principles and

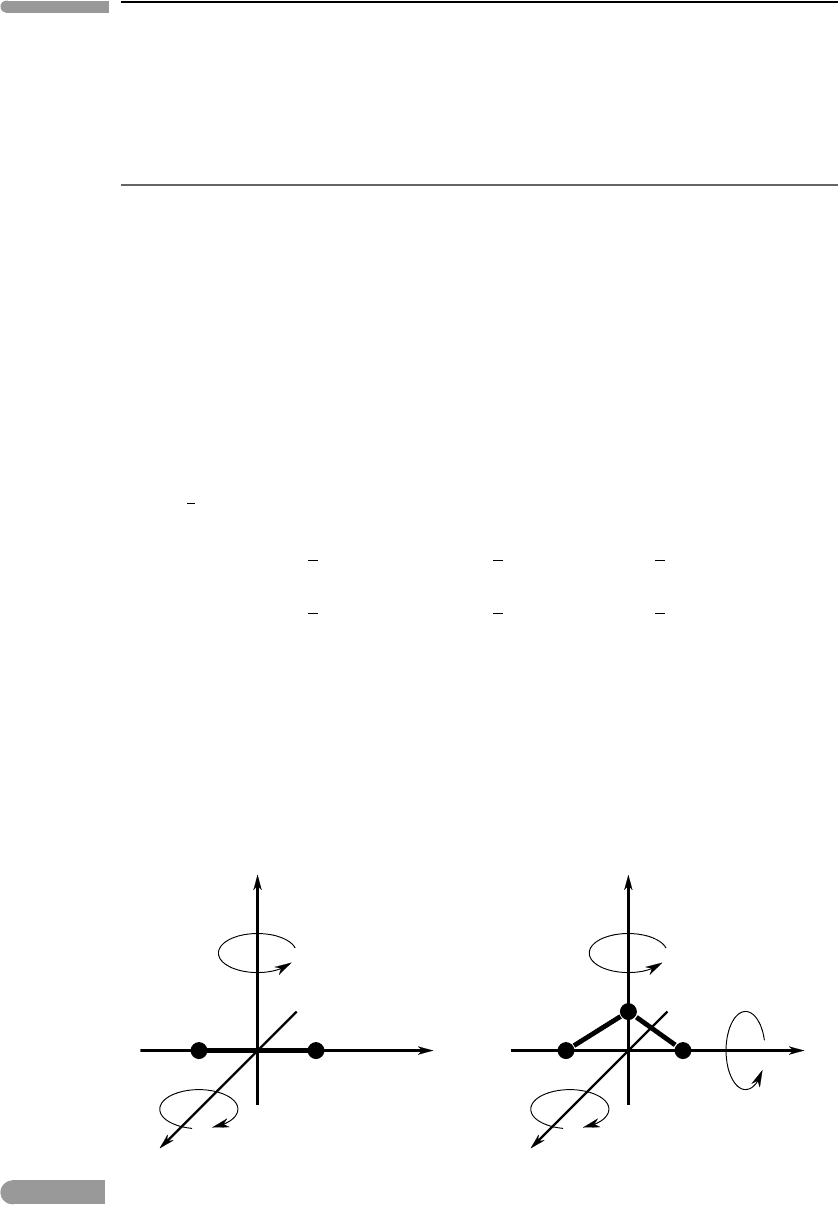
60 Energy in planetary processes

formalism of statistical mechanics that would allow us to do that for an ideal gas can be

used to derive equations of state for materials of planetary interest at very high pressures

and temperatures, that may be experimentally inaccessible.

1.14.2 Degrees of freedom and heat capacities of polyatomic gases

The internal energy function given by equation (1.112) is appropriate for a monatomic ideal

gas, but it must be modified for diatomic and polyatomic gases. This is so because, if the

molecule contains more than one atom, then additional degrees of freedom are possible,

and by the principle of equipartition of energy each of these additional degrees of freedom

carries an additional amount of energy. For example (Fig. 1.13), a diatomic molecule has

non-negligible moment of inertia relative to two orthogonal axes perpendicular to the atomic

bond, and a polyatomic molecule (unless the atoms are arranged in a straight line) has non-

negligible moment of inertia relative to three orthogonal axes. This means that diatomic and

polyatomic molecules have kinetic energy of rotation in addition to that of translation, and

each of the rotation axes adds a degree of freedom. As molecules collide with one another

kinetic energy is exchanged between translational and rotational degrees of freedom, and

by the principle of equipartition of energy all degrees of freedom carry the same amount of

energy:

T . The corresponding internal energies are, thus:

diatomic

RT (translational) +

RT (rotational) =

polyatomic

RT (translational) +

RT (rotational) =

RT .

(1.113)

The constant volume heat capacities of ideal gases are, therefore: 3/2R,5/2R and 3R, for

monatomic, diatomic and non-linear polyatomic ideal gases, respectively. Heat capacities

can be determined directly by experiment and are a test of the predictions of the microscopic

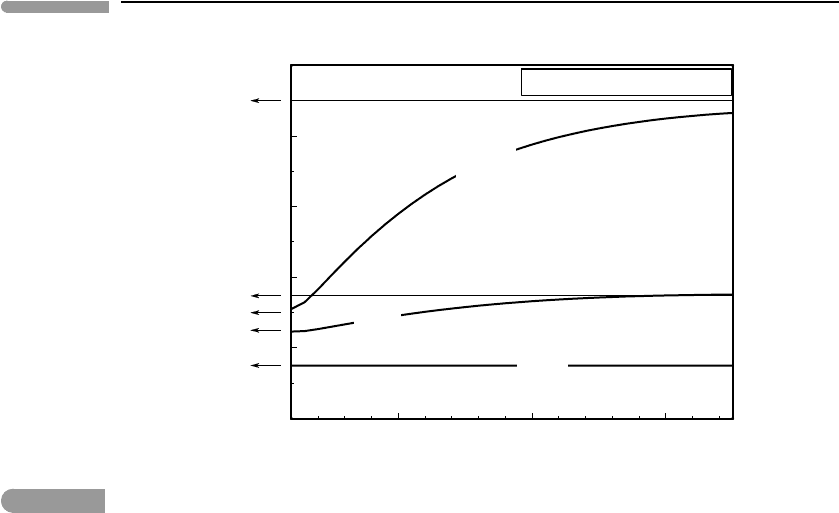
description of ideal gases. Figure 1.14 shows measured constant volumes heat capacities

at low pressure as a function of temperature, for a monatomic gas (neon), a diatomic gas

(nitrogen) and a polyatomic gas with a three-dimensional molecule (ammonia). The low

pressure constraint is what makes the behavior of the gases approach that of ideal gases,

Fig. 1.13

Rotational degrees of freedom for a linear molecule and a non-linear molecule.

61 1.14 Internal energy

1000 2000 3000

T (K)

3/2

5/2

6/2

7/2

Constant volume heat capacities

Fig. 1.14

Measured constant volume heat capacities for a monatomic gas (Ne), a diatomic gas (N

) and a polyatomic gas with

non-linear molecules (NH

). Data from NIST Chemistry WebBook. The values expected from kinetic theory are 3/2 R,

7/2 R and 9 R, respectively. Heat capacity is plotted as the non-dimensional variable C

/R.

by keeping them far from their condensation conditions. The agreement of the measured

values with those predicted by kinetic theory is essentially perfect for neon. For nitrogen

the agreement is good at temperatures up to approximately room temperature (∼300 K) but

then C

increases smoothly and reaches a plateau of approximately 7/2R. In the case of

ammonia there is good agreement at low temperature (200–300 K), and then, as for nitrogen,

increase and reaches a plateau, in this case close to 9R.

Do these discrepancies mean that the premises that we used to calculate C

for gases

other than monatomic gas are incorrect? Well, no, what it means in this case is that they are

incomplete. In other words, gases that contain more than one atom in their molecules have

other degrees of freedom in addition to those corresponding to translation and rotation. These

are called vibrational degrees of freedom, and they arise from the fact that atomic bonds are

not rigid, but can stretch, contract and bend as an elastic material (e.g. a spring), and behave

like harmonic oscillators. These oscillations carry energy and thus represent additional

degrees of freedom. The principle of equipartition of energy applies to vibrational degrees

of freedom too, but there are two important differences with translational and rotational

degrees of freedom, which we can see by examining Fig. 1.14 in some detail.

First, vibrational degrees of freedom in gases are inactive at low temperature and begin

to carry energy only as temperature rises. In other words, gas molecules must have a

minimum amount of kinetic energy before collisions are able to transfer some of this energy

to vibrations of the atomic bonds (if you suspect a connection with quantum mechanics here

you are right). The situation is different for solids and liquids, in which vibrational modes

are important at relatively low temperatures, simply because translational and rotational

degrees of freedom do not exist in them (although liquids have additional complexities).

Second, in the diatomic gas there is only one atomic bond, and thus there can only be

one vibrational degree of freedom, which corresponds to stretching of the atomic bond.

62 Energy in planetary processes

Heat capacity for diatomic nitrogen levels off at a value of approximately 7/2R, suggesting

that the vibrational degree of freedom carries twice as much energy as the translational

and rotational ones, i.e. k

T. This is indeed the case, and the explanation is that harmonic

oscillators (such as an atomic bond that stretches and contracts, or a pendulum, which is

mathematically equivalent) carry both kinetic and potential energy, and equipartition of

energy causes each of these energy modes to have an energy content of

T . In the case

of ammonia the difference between the measured high-temperature heat capacity (9R) and

the heat capacity predicted from translation and rotation only (3R) indicates that there are

six vibrational degrees of freedom, which include stretching of the N–H bonds, changes in

the angles between N–H bonds, and bending relative to a plane containing all four atoms.

The general rule for gases is that molecules have a total of 3n degrees of freedom, where

n is the number of atoms in the molecule. Of these, 3 degrees of freedom are always

translational, and either 2 or 3 are rotational, depending on whether the molecule is linear

or not (Fig. 1.13). Each of these degrees of freedom carries an energy equal to

T . The

remaining 3n −5 (linear molecule) or 3n − 6 (non-linear molecule) degrees of freedom

are vibrational and each carries an energy of k

T. Translational and rotational degrees of

freedom are always active, whereas vibrational degrees of freedom only become active (or

“excited”) above a certain temperature.

Constant volume heat capacities for ideal gases follow immediately from the generaliza-

tions given in the previous paragraph. In most planetary sciences applications, however, we

are interested in C

rather than C

V ,

and these are also easily derived. From the definition

of enthalpy we have:



∂H

∂T





∂E

∂T





∂V

∂T



. (1.114)

Using identity (1.3.12)inBox1.3 and the fact that, for an ideal gas, (∂E/∂V )

=0, we see

that:



∂E

∂T





∂E

∂T





∂E

∂V





∂V

∂T



(1.115)

and from the ideal gas EOS:



∂V

∂T



=R (1.116)

so, for an ideal gas:

+R. (1.117)

The extra amount of energy, R per Kelvin per mol, is a macroscopic contribution from

expansion work and does not reflect a change in the microscopic state of the system.

For gases that cannot be assumed to behave ideally equation (1.117) is not valid, but the

appropriate equation can always be derived from the equation of state, starting from equation

(1.114) which is true in general. Thus, with some important additional considerations, the

physical concepts developed in this section are the basis for understanding and quantifying

the behavior of real fluids at high pressures and temperatures, something that we will do in

Chapter 9.

63 1.14 Internal energy

1.14.3 Heat capacities of solids

In a crystalline solid there are only vibrational degrees of freedom. The atoms have fixed

positions in the crystalline lattice. They vibrate about their equilibrium positions, but they

can neither translate not rotate. Each atom can vibrate in three independent directions. We

could thus expect the heat capacity of crystalline solids to be approximately 3R per gram

atom, reflecting the three vibrational degrees of freedom of each atom, and the fact that

each vibrational degree of freedom carries an energy of k

T per atom. The molar heat

capacity of a substance that contains n atoms in its molecule should thus be 3nR. This has

been empirically known to be the case since the nineteenth century. It is known as Dulong

and Petit’s law, but it works only for temperatures comparable to or greater than room

temperature.

Figure 1.15 shows constant pressure heat capacities for a few minerals (C

and C

for

solids differ by a very small amount, because of the incompressibility of solids, see Chapter

8). They all approach Dulong and Petit’s behavior at high temperature (∼10

K), but heat

capacities fall off fairly steeply with decreasing temperature. The data confirm the general

microscopic picture (atoms in a solid have vibrational degrees of freedom only) but also

show that some fundamental physics is missing from the picture. The missing ingredient is

quantum mechanics, and although the details are beyond the scope of this book a qualitative

understanding of the behavior depicted in Fig. 1.15 will become important in subsequent

discussions. Atomic vibrations in a crystal are quantized, meaning that only some definite

energy levels are allowed. At low temperature the allowed energy levels are few and far

apart, and degenerate to a single energy level as absolute zero is approached. The number

of allowed energy levels increases with temperature, and as this happens so does the heat

400 600 800 100

T (K)

FeS

MgSiO

SiO

CaMgSi

(PO

)

21 x 3

10 x 3

7x3

5x3

3x3

Constant pressure heat capacity of solids

Fig. 1.15

Constant pressure heat capacities for pyrite, enstatite, forsterite, diopside and ﬂuorapatite. Horizontal lines show

Dulong and Petit’s approximation, labeled next to the arrows: the number of atoms in the formula times the number

of vibrational degrees of freedom per atom (=3). Measured heat capacity data from Robie and Hemingway (1995).

Heat capacity plotted as the non-dimensional variable C

/R.

64 Energy in planetary processes

capacity. Above a certain temperature the quantum energy levels become so close together

that the classical continuous approximation – Dulong and Petit’s law – becomes valid. This

temperature is characteristic for each substance and is known as the Debye temperature,

. The Debye temperature for most minerals is of the order of several hundred to ∼10

Heat capacity becomes a weak function of temperature above θ

, as shown by Fig. 1.15.

Interestingly, Dulong and Petit’s approximation also works for some liquids. For example,

the heat capacity of water is ∼75JK

−1

mol

−1

≈ 9R, corresponding to 3R for each of the

three atoms in the H

O molecule.

1.15 An overview of the properties of matter and equations of state

Equations of state (EOS) are an essentialcomponent in the study of the physics and chemistry

of planetary bodies. We will discuss different types of EOS in considerable detail in Chapters

8 and 9. Here we define some concepts about the possible states of matter in planetary

environments. This will allow us to better define the P –V –T ranges over which different

types of EOS are applicable. Solids and liquids are condensed phases, whereas gases are

non-condensed phases. Both liquids and gases are fluids. Gases are non-condensed fluids,

which means that they expand indefinitely as pressure decreases, whereas we call liquids

condensed fluids because, as solids, they do not behave in this manner. These contrasting

macroscopic behaviors arise from differences between condensed and non-condensed fluids

in the relative magnitudes of the intermolecular potentials (or forces), compared to thermal

energy. A vapor is a gas in equilibrium with its liquid, and a melt is a liquid in equilibrium

with its solid. For all substances it is an empirical observation that, as temperature increases,

the material properties of liquid and vapor at equilibrium approach each other, until the two

phases become indistinguishable at a temperature called the critical temperature. Above

the critical temperature a single fluid phase is stable, called a supercritical fluid.

Here we describe the behavior of matter in terms of temperature and density (i.e. the

inverse of volume). Density is a better choice than pressure for this exercise because we

can relate it directly to a description of the material at the atomic scale, something which is

not generally the case with pressure. The arguments and conclusions are summarized in a

density–temperature diagram, Fig. 1.16, which is rather busy and will take some explaining.

The physical inspiration for this discussion comes from Shalom et al.(2002), who present

detailed mathematical arguments; I have added the planetary applications. A review of

recent developments in the high density region of the diagram is given by Drake (2010).

The horizontal coordinate in the diagram is temperature in Kelvin. Let the thermal energy of

microscopic particles (molecules, atoms, ions, etc.) be ε

. From our discussion in Section

1.14 we conclude that ε

is of order k

T, which we symbolize with the ∼ symbol, i.e.

T .

∼ k

T. The justification for this statement is that particles carry an energy equal to

T per degree of freedom, and the number of degrees of freedom is a small number, of

order 1–10.

At sufficiently high temperature atoms become ionized as a result of interatomic col-

lisions. This happens when their thermal energy is of the same order as their ionization

energy, i.e., the energy required to detach an electron from an atom. By equating the ion-

ization energy of an element to k

T we can estimate the temperature at which thermal

ionization takes place. Note, however, that because energies of individual atoms are not

all the same but follow a statistical distribution (e.g., Fig. 1.12), ionization actually takes

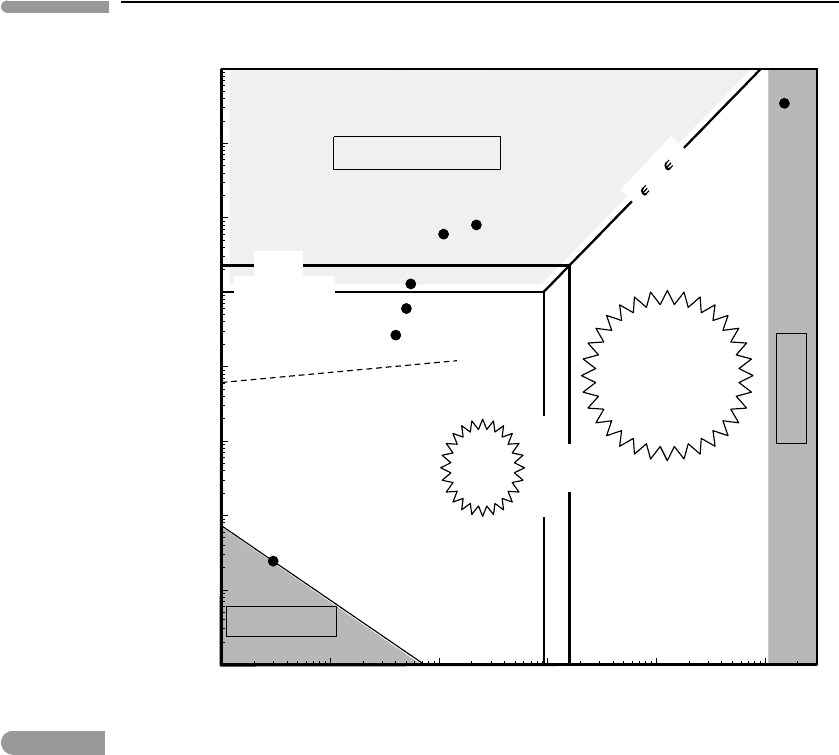
65 1.15 An overview of the properties of matter

Temperature (K)

Particle density (m

–3

)

Earth atmosphere

Earth CMB

Earth deep core

Uranus & Neptune

deep interior

Saturn deep interior

Jupiter deep interior

Solar core

Fe, Si, Mg, C

H, O

electron degeneracy

Ideal gas EOS

Ideal gas at 1 bar

non-condensed fluids

condensed fluids and solids

Ideal gas EOS

Non-ideal gases

Here

there

dragons...

...and

here

too

Fig. 1.16

Density–temperature diagram of matter. Dark gray regions correspond to ideal gas behavior. Pressure ionization

occurs in the light gray region. The lines labeled “H, O” and “Fe, Si, Mg, C” represent approximate ionization conditions

caused by temperature and pressure. CMB =core–mantle boundary.

place over a temperature range. The vertical lines labeled “H, O” and “Fe, Si, Mg, C” show

characteristic ionization temperatures for these most important of planet-forming elements.

Many other abundant elements plot within this range, the only important exception being

helium, which has an ionization energy almost twice that of hydrogen. Thermal ionization

occurs at temperatures of order 10

K, which are not attained in any planet in the Solar

System, but may be possible inside large extrasolar planets and brown dwarfs (failed stars).

Most of the solar interior is of course ionized.

Density is shown on the vertical axis as particle density, i.e. number of particles per unit

volume. This is simply Avogadro’s number divided by molar volume, and has units of m

−3

Using these units we can compare the degree of packing independently of particle mass.

The figure shows some reference values. An ideal gas at 1 bar and 298 K (e.g., the terrestrial

atmosphere) has a particle density of ∼2.4 ×10

−3

. The variation of this number with

temperature at a constant pressure of 1 bar, i.e. the ideal gas law, is shown in the diagram

with a negatively sloping line. The ideal gas EOS reproduces P –V –T relations to a high

degree of accuracy for conditions below this line (P<1 bar) and perhaps over a narrow

66 Energy in planetary processes

interval above the line. With increasing particle density the behavior of real gases diverges

from the predictions of the ideal gas EOS, owing to the existence of interatomic potentials,

i.e. attractive and repulsive forces. Up to particle densities of ∼10

–10

−3

, substances

behave as non-condensed fluids (i.e., gases) even if their densities are higher than what we

typically associate with a gas.

Condensation occurs at particle densities of ∼10

−3

, with overlapping ranges for

liquids and solids. Condensed matter is orders of magnitude less compressible than gases,

a fact that is expressed in Fig. 1.16 by the (apparent) proximity of a wide range of con-

densed planetary materials. The examples shown are: Mg

1.8

0.2

SiO

at the conditions of

the Earth’s core–mantle boundary (Chapter 8), an H

O–CH

–NH

mixture at conditions

thought to represent the deep interiors of Uranus and Neptune, Fe in the Earth’s inner core,

and H–He mixtures in Jupiter’s and Saturn’s deep interiors. These examples are representa-

tive of the upper density–temperature bounds likely to be encountered in the Solar System,

with the exception of the solar interior, which is also shown for comparison.

At particle densities somewhat above 10

−3

it is necessary to consider quantum

effects. We define the quantum energy, ε

, for a particle of mass m and momentum p

as ε

= p

/m.If particles are packed with a particle density n, then each particle occupies

a volume n

−1

, which means that there is an uncertainty in the position of the particle of

order n

−1/3

.According to the uncertainty principle the relationship between p and n is given

(approximately) by:

−1/3

≈h, (1.118)

where h is Planck’s constant. We then get for the quantum energy:

≈

2/3

. (1.119)

For an electron with mass m

, accounting for the fact that each volume element can be

occupied by at most two electrons with opposite spins, and allowing for spherical symmetry,

the quantum energy becomes the Fermi energy, ε

, given by:

2/3





2/3

. (1.120)

If the Fermi energy exceeds the ionization energy and ε

>ε

then the material undergoes

pressure ionization. This takes place even if the thermal energy of the material is lower than

its ionization energy, because bound electrons are excluded by the uncertainty principle from

occupying the same volume element. The resulting condition is termed electron degeneracy.

The horizontal lines labeled “H, O” and “Fe, Si, Mg, C” show the approximate densities

at which electron degeneracy can be expected to occur in planetary materials. Much of

Jupiter’s and Saturn’s interiors are likely to consist of pressure-ionized hydrogen, and some

degree of pressure ionization may also occur in the Earth’s deeper core. Most of the core, as

well as the Earth’s mantle, and the entire volume of the ice giants (Uranus and Neptune) are,

in contrast, composed of non-degenerate matter. Given that pressures in the other terrestrial

planets are lower than in the Earth’s interior this conclusion also applies to them. EOS for

degenerate matter are needed in order to model the interiors of the giant planets.

In contrast to “cold” dense matter, “hot” dense matter (ε

>ε

) is not degenerate. This

includes the entire solar interior. At temperatures of order 10

K interatomic potentials are

negligible compared to thermal energy. Under such conditions matter consists of a highly

67 Exercises for Chapter 1

ionized plasma that is accurately described as a monatomic ideal gas (more on this in Chapter

2). We are left, as the figure shows, with a wide range of intermediate temperatures and

densities in which the behavior of matter is poorly understood and for which equations of

state are very complex, if they exist at all. Fortunately, these regions are of little interest to

planetary scientists. Focusing now on the range of conditions for non-degenerate matter in

planetary interiors (T < 10

K, n < 10

−3

), which is what we will mostly be concerned

with, we can identify three regions that require distinct equations of state. At very low

densities the ideal gas EOS is all we need. At the other end, a class of EOS that will be

introduced in Chapter 8 is generally appropriate for the entire range of densities of non-

degenerate condensed matter, both solids and liquids. This leaves the intermediate density

range, roughly between 10

and 10

−3

, occupied by non-ideal gases. Equations of state

for non-ideal gases are discussed in Chapter 9.

Exercises for Chapter 1

1.1 A mass m

of ice at temperature T

is added to a mass m

of water at temperature T

inside a perfectly isolated container. Let the heat capacities of ice and water be C

p,i

and C

p,w

, and the enthalpy of fusion of ice be 

H > 0. Derive a set of criteria to

decide what the final equilibrium state of the system is, i.e. pure ice, pure water or

ice + water.

1.2 Calculate the gravitational potential energy stored in the Earth’s largest active volcano

(Mauna Loa) and in the Solar System’s largest volcano (Olympus Mons in Mars).

Assume that Mauna Loa is a cone with a basal radius (on the floor of the Pacific

Ocean) of 50 km, and an elevation of 10 km relative to the ocean floor, and Olympus

Mons a cone with a radius of 600 km and an elevation of 27 km. The gravitational

accelerations of Earth and Mars are 9.8 and 3.7 m s

−2

. Assume that Mauna Loa is

2 ×10

years old. Calculate the average power expended in building up Mauna Loa.

Assuming that this rate of storage of potential energy is characteristic of large basaltic

shield volcanoes, estimate how long the building of Olympus Mons may have taken.

How does this compare with the building time of Olympus Mons if you assume the

same mass supply rate as in Mauna Loa? Discuss the relative merits of extrapolating

terrestrial mass supply rate or energy supply rate to Mars. Compare the rate of storage

of potential energy in Mauna Loa with the power output of the Hawaiian hot spot,

∼10

−1

. Comment on your results.

1.3 What is the potential energy stored in a rod-shaped asteroid, 100 × 50 × 50 km, with

density = 3000 kg m

−3

? The stable shape of the asteroid is a sphere with the same

volume.

1.4 Derive the formula for kinetic energy (equation (1.12)) by considering conservation

of energy of a free-falling body in a uniform gravitational field.

1.5 Consider the asteroid–Earth collision (Worked Example 1.2). What is the relationship

between m and M that results in the greatest dissipation of kinetic energy? You can

do this formally, by maximizing the function in equation (1.15), or intuitively, from

symmetry considerations.

1.6 What is the maximum amount of power that can in principle be harvested from wind

with a velocity v, by a wind turbine with diameter d ? The actual power output of the

turbine must be less than this, why?