Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

48 Energy in planetary processes

Fig. 1.8

Frictional heating of a volume Az by dissipation of frictional work on a fault plane of area A (grey).

the frictional force on the system is dW . The work performed by the system against the

frictional force is thus −dW . A fault or shear zone moves when the force generated by the

shear stress component, τ , equals the frictional force. If the total surface area of the fault

plane is A then the frictional force is τ A. Calling the displacement along the fault dx, dW

is given by:

dW = τAdx, (1.78)

where, because frictional forces always act in the direction of displacement, I have been

sloppy and neglected the vector notation (see Box 1.1). Faulting can be treated as a constant

pressure process, because pressure inside a planet is determined by depth and the magnitude

of the instantaneous motion along a fault or shear zone is generally negligible compared to

depth. We thus write dE as follows:

dE = dH −PdV = C

dT −PdV (1.79)

so:

dT −PdV =−PdV −

(

−dW

)

. (1.80)

Substituting in (1.78):

dT = τAdx. (1.81)

Note that C

in this equation is the extensive variable, i.e. the total heat capacity of the

mass of heated rock. Let V =Az be the total volume of heated rock (Fig. 1.8), and N be the

number of mols of substance contained in this volume. If we symbolize the molar volume

of the substance with V and its molar heat capacity with C

, then:

N =

. (1.82)

Substituting in (1.81) and rearranging we arriveat an equation in terms of intensive variables:

dT =

τV

dx, (1.83)

49 1.13 Enthalpy associated with chemical reactions

from which we can also derive the rate of temperature increase, dT/dt (where t = time):

τV

. (1.84)

The value of τ is determined either by the brittle shear strength for rocks (for a brittle fault)

or by the yield strength for a given ductile strain rate for a ductile shear zone; typical values

in both cases are of the order of 100 to a few 100 bar. Given that all three parameters: τ ,V

and C

vary within fairly restricted ranges for planetary materials, the rate of temperature

increase is controlled primarily by the width of the heated rock volume, z. Because the length

scale z is controlled by heat diffusion (Chapter 3) we can expect that it varies inversely with

the strain rate, which we can represent by dx/dt. We can thus expect a very strong dependency

of dT/dt on dx/dt, because as strain rate increases, z decreases and both effects combine to

make dT/dt larger. The ductile behavior of rocks is strongly temperature-dependent, with

viscosity decreasing exponentially with increasing temperature (see for instance Turcotte

& Schubert, 2002, Chapter 7). A positive feedback mechanism results, that focuses ductile

deformation in relatively narrow shear zones, in which most of the temperature increase,

and consequent lowering of the viscosity, take place.

As a numerical example, consider “slickensides”, that probably form as a result of instan-

taneous heating at a fault during brittle failure (i.e. earthquakes). For a slickenside width z

=5 mm, and fault motion during an earthquake x =1 m we obtain a maximum temperature

increase (for τ of a few hundred bars) T ≈ 2000 K. Fault motions during earthquakes

may last for only a few seconds, so that the heating rate may be of the order of hundreds of

degrees per second.

1.13 Enthalpy associated with chemical reactions

1.13.1 Enthalpy of reaction and enthalpy of formation

Phenomena such as condensation of solids in the solar nebula, generation and crystallization

of magmas, metamorphism, weathering, diagenesis, precipitation of carbonate minerals

from seawater and crystallization of evaporites, are chemical reactions. The essence of

a chemical reaction is that atoms of certain elements are transferred among phases, or

rearrange themselves into different molecules inside a homogeneous phase (e.g. chemical

reactions between gas species in a homogeneous atmosphere). Atomic bonds are broken

and form during chemical reactions, as a result of which there is a net surplus or deficit

of energy that is exchanged with the environment. The macroscopic manifestation of these

microscopic energy transactions is the enthalpy change associated with a chemical reaction.

This enthalpy is called the enthalpy of reaction and is denoted by 

H. Enthalpy of reaction

is the amount of heat liberated or absorbed during a chemical reaction at constant pressure

and constant temperature. In Chapters 4 and 5 we will arrive at a precise and rigorous

definition of chemical equilibrium and we will see that enthalpy of reaction is an important

part of that definition and of the algebraic procedure by which we calculate the location of

chemical equilibria. Enthalpy of reaction behaves as latent heat: it is heat exchanged without

a change in temperature. You may think that this statement cannot possibly be correct, as

you are probably familiar with endothermic and exothermic reactions, during which the

temperature of the system decreases and increases, respectively. The answer to this puzzle

50 Energy in planetary processes

is that these temperature changes are caused by the fact that the rate of heat transfer is much

slower than the rate of chemical reaction. For example, during an exothermic reaction

enthalpy is liberated at a rate faster than the rate at which heat can be carried away from the

site where the reaction takes place. As a result, latent heat (enthalpy of reaction) is converted

to sensible heat (temperature increase).

We can write the algebraic definition of enthalpy of reaction by considering a generic

chemical reaction between reactant A and product B:

A →B. (1.85)

The enthalpy of reaction at a given T and P is the difference between the enthalpy of B and

the enthalpy of A at those conditions:



H = H

−H

. (1.86)

But what are the enthalpies of A and B? The First Law of Thermodynamics codifies the

law of energy conservation: it states that the total amount of energy is conserved, but says

nothing about the absolute magnitude of energy. A more formal statement of this fact is that

the First Law of Thermodynamics (equation (1.55)) is a differential equation and, as such,

it admits an infinite number of solutions that differ by an additive constant (the integration

constant). This is not a problem, because all we care about is the difference in enthalpy

between different states of a system. This is true in general: even though we did not state

it explicitly, in all examples that we have discussed thus far we have calculated differences

in enthalpy, internal energy or other types of energy, and not their absolute values. In the

case of a chemical reaction, we are not interested in the absolute magnitudes of H

, all we are interested in is 

H . Because enthalpy is a state variable, the First Law of

Thermodynamics assures us that, as long as we define individual enthalpies relative to the

same reference level, the value of 

H at any given T and P is unique and well defined.

We need to define some arbitrary reference level relative to which we will measure

enthalpies – the integration constant, if you wish. We did just this when we defined poten-

tial energy = 0 at infinity (Section 1.3.1), or when we specified that we were measuring

kinetic energy relative to a reference frame fixed to the Earth (Section 1.3.2). The universal

convention for chemical systems is to set the enthalpy of all pure chemical elements in

their stable configuration at 298.15 K and 1 bar equal to zero. The “stable configuration”

requirement is important. We cannot define rigorously what this means until after we have

defined chemical equilibrium (Chapters 4 and 5), but we can study examples that make the

meaning clear. The enthalpy of diatomic oxygen at 298.15 K and 1 bar is zero, because O

is the stable oxygen species at those conditions. In contrast, the enthalpies of atomic oxygen

(O) and of ozone (O

) at 298.15 K and 1 bar are not zero. For carbon, graphite has zero

enthalpy at 298.15 K and 1 bar. The enthalpy of pure elements in their stable configurations

at any other P–T combination is not zero either.

We define the enthalpy of formation of a substance (compound or element) at the reference

pressure and temperature as the value of 

H for the reaction that forms the substance from

the elements (in their stable configurations) at 298.15K and 1 bar. In the thermodynamics

literature there are, unfortunately, different symbols in use for this quantity. In this book we

will symbolize the enthalpy of formation at the reference pressure (1 bar) and temperature

(298.15 K) by 

1,298

. This notation is not in widespread use. Enthalpy of formation at

298.15 K and 1 bar is one of the values that are listed in tables of thermodynamic properties

of substances, and is commonly symbolized 

. The convenience of adding the actual

51 1.13 Enthalpy associated with chemical reactions

values of the reference pressure and temperature, as I do here, will become clear in due

course, as will the meaning of the

superscript which appears in both notations.

We will not discuss in this book how enthalpies of formation are measured, as excellent

discussions are available in classical textbooks on chemical and geochemical thermody-

namics (see, for example, Anderson, 2005, Chapter 5), but we will look at some examples

to make the concept clear. The enthalpy of formation, 

1,298

, of liquid H

O is equal to



H for the reaction:

⇒H

liquid

. (1.87)

at 298.15 K and 1 bar. Because this is a constant pressure process, 

1,298

is simply the

heat liberated when 1 mol of liquid water forms from a stoichiometric mixture of hydrogen

and oxygen gas at 298.15 K and 1 bar (see equation (1.62)). Similarly, 

1,298

of diamond

is the heat exchanged by the following polymorphic transformation at 298.15 K and 1 bar,

per mol of carbon:

graphite

⇒C

diamond

. (1.88)

The enthalpy of formation of graphite is zero. Whether or not the formation reaction can

actually take place at 298.15 K and 1 bar, or whether or not the substance in question is

stable at those conditions, is not important. For example, we can define 

1,298

for H

gas even though H

O gas is not stable at 298.15 K and 1 bar – although of course, the

enthalpy of formation of H

O gas at the reference conditions 298.15 K and 1 bar is different

from that of liquid H

O at the same conditions. Defining and evaluating 

1,298

for a

substance that is not stable at 298.15 K and 1 bar is no more a problem than the fact that it

is not possible to locate a body at infinity, yet infinity provides a convenient reference level

for potential energy.

The quantity 

1,298

is sometimes called the standard state enthalpy of formation.

Unfortunately, the phrase “standard state” applied to thermodynamic variables (including

enthalpy) can also have another, quite different, meaning. We will come across this alternate

meaning in Chapter 5 and we will see that the intended meaning is commonly (but not

always) evident from the context. I will make the meaning explicit whenever there is a

possibility of confusion (for an in-depth look at this and other terminology issues, see

Anderson, 2005). More trivially, why choose the reference conditions at a strange value

such as 298.15 K? Because this temperature corresponds to 25

◦

C, which historically has

been considered “standard” room temperature (arbitrarily so, and uncomfortably warm in

the view of this writer). I usually abbreviate 298.15 as 298.

1.13.2 Enthalpy of reaction as a function of temperature

I will use this example to describe the procedure that is used to calculate 

H at any

arbitrary temperature and 1 bar. These calculation procedures will be used in later chapters

to calculate chemical equilibrium.

Consider the problem of condensation of solids in the solar nebula. During the forma-

tive period of planetary systems the chemical elements are progressively extracted from

a gas phase by formation of solid phases. Which phases and elements condense depends

on temperature. Refractory phases such as perovskite (CaTiO

) and corundum (Al

)

condense at temperatures of the order of 1600 K, whereas very volatile phases (generically

52 Energy in planetary processes

called “ices”) in which the chief constituents are C, O, N and H condense at much lower

temperatures, 300 K or less. Water ice is one of the most abundant of planetary “ices”. If

condensation takes place at pressures lower than the pressure of the triple point of H

(∼0.006 bar), then the solid phase forms directly by reaction of chemical species in the gas

phase, because the liquid phase is not stable at those conditions (Chapter 6). Suppose that

we want to know the enthalpy change (heat released) during condensation of H

O ice from

gaseous H

and O

at 273 K and 10

−4

bar. The strategy to calculate the enthalpy change

for this reaction is to break up the problem into two parts. First, we calculate the enthalpy

of reaction at the temperature of interest (273 K in this case) and the reference pressure

of 1 bar. Let us call this enthalpy of reaction 

1,T

. Then, we calculate how enthalpy of

reaction varies as a function of pressure at a constant temperature of 273 K, integrate this

function from 1 bar to the pressure of interest (in this case, 10

−4

bar) and add the result to



H at 273 K and 1 bar. Symbolically:



P ,T

=

1,T





∂

(



)

∂P



dP , (1.89)

where, for the example that we are considering, T = 273 K and P = 10

−4

bar. Here we

will look only at the first part of the problem, i.e. calculation of the enthalpy of reaction at

273 K and 1 bar: 

1,273

. The pressure integral (second term on the right-hand side of

equation (1.100)) will be discussed in Chapters 5, 8 and 9, because it relies on concepts that

we have not discussed yet. Here we will focus on the fact that, even though equilibrium

condensation of the solid from the gas does not occur at 1 bar (because liquid is stable at

that pressure), calculation of the enthalpy change at 1 bar is always possible.

Relative to 

1,298

of liquid H

O (equation (1.87)), there are two differences in



H for the reaction that forms H

O ice from H

and O

gas at 273 K: the temperature is

different and the H

O phase is different. In order to visualize how to proceed it is best to

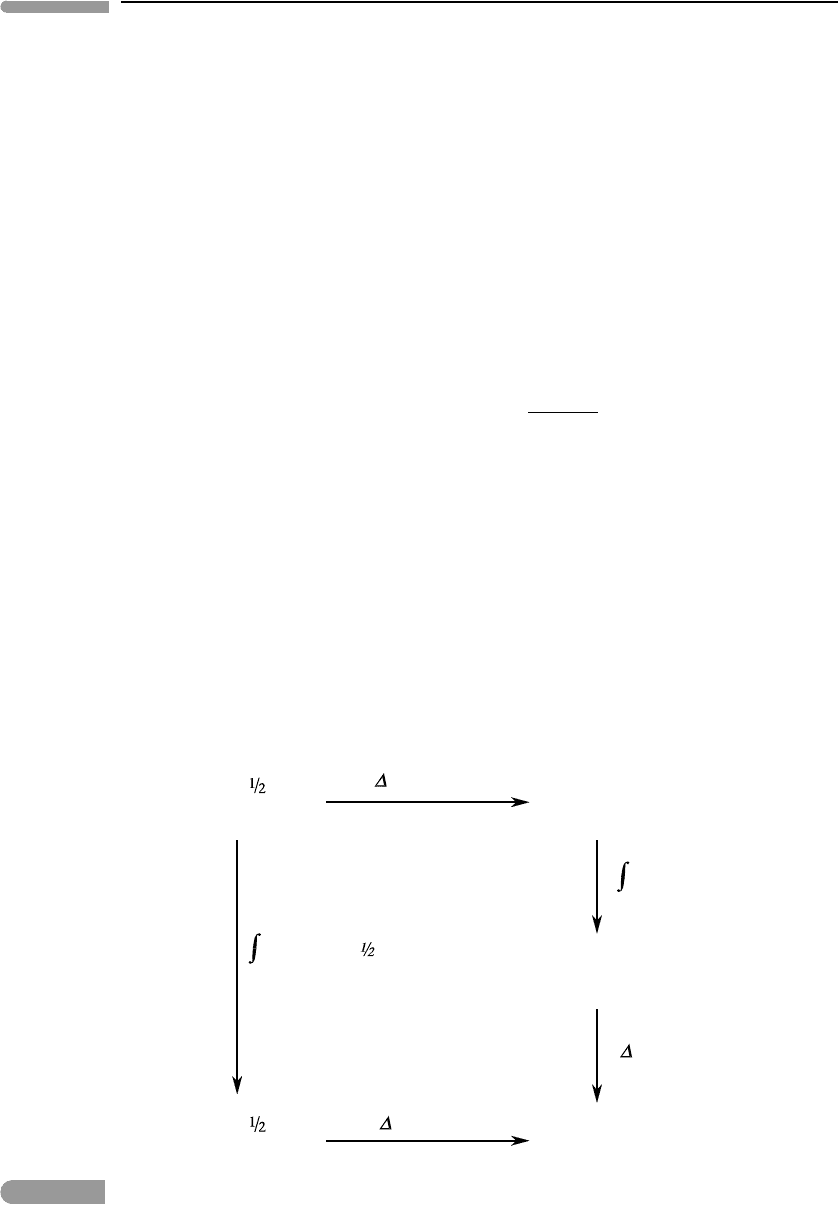
draw a diagram (Fig. 1.9). Because enthalpy is a state variable its value is independent of

+ O

1 bar, 298.15 K

O (liquid)

1 bar, 298.15 K

O (liquid)

1bar,273K

O (ice)

1 bar, 273 K

+ O

1 bar, 273 K

1, 298

1, 273

freezing

298

273

P, H

liquid

298

273

[ C

P,H

+ C

P,O

] dT

Fig. 1.9

Enthalpy of condensation of H

O ice from the elements at 273 K and 1 bar.

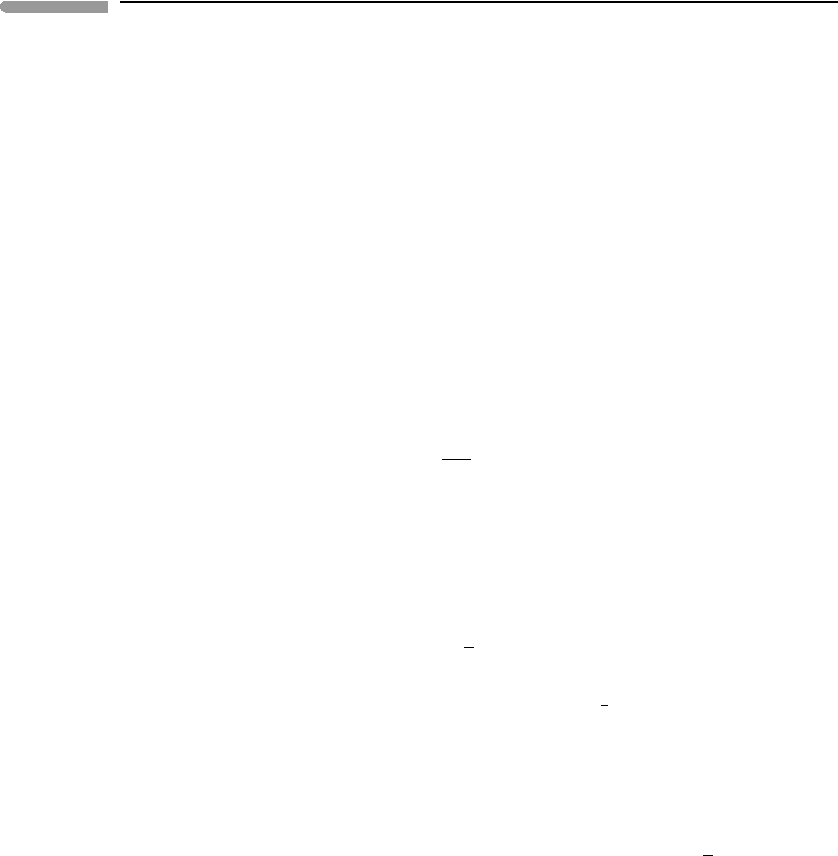
53 1.13 Enthalpy associated with chemical reactions

the path that we use to calculate it, it only depends on the state of the system that we are

considering. In our case the state of interest is H

O ice at 273 K and 1 bar. The diagram

(Fig. 1.9) shows that, starting from an initial state consisting of hydrogen and oxygen gas

at 298 K and 1 bar (the reference conditions at which the enthalpies of the elements are

zero), there are two paths by which we can arrive at the desired final state. One way is to

form liquid H

O at 298 K and 1 bar, then cool the liquid to 273 K, then freeze the liquid at

273 K to ice at 273 K. The total enthalpy change along this path is:

H

=

1,298



273

298

P,liquidH

dT +H

freezing

, (1.90)

where 

1,298

is the enthalpy of formation of liquid H

O (equation (1.87)), H

freezing

−H

melting

is the heat given off when water freezes to ice at 273 K and 1 bar, and the change

of enthalpy associated with an isobaric change in temperature, i.e. the middle term in the

right-hand side of equation (1.90), is given in general by:

(

)

(

)





∂H

∂T



dT = H

(

)



dT . (1.91)

Another way to arrive at ice at 273 K and 1 bar is to cool the gas mixture to 273 K and

then form ice directly by reaction between the gases at this temperature. This is the process

that takes place in the solar nebula, and the one that we want to calculate the enthalpy of

reaction for: 

1,273

. The enthalpy change along this path (Fig. 1.9) is:

H



273

298

P ,H

dT +



273

298

P ,O

dT +

1,273

. (1.92)

The heat capacity integral for O

is preceded by a factor of

, which is the stoichiometric

coefficient for O

in the balanced chemical reaction – recall that C

is the molar heat

capacity. Stoichiometric coefficients are always present, but they are 1 for H

and H

Now, because enthalpy is a state variable, it must be H

=H

, and we see immediately

that:



1,273

=

1,298

+H

freezing



273

298



P,liquid H

−C

P ,H

−

P ,O



dT .

(1.93)

We are also interested in 

H for reactions in which no pure elements take part. For

example, the following reaction among spinel (MgAl

), enstatite (Mg

), forsterite

(Mg

SiO

) and pyrope (Mg

) is an end-member model for the transition between

spinel lherzolites and garnet lherzolites in the mantles of the Earth and other terrestrial

planets:

MgAl

+2Mg

⇒Mg

SiO

+Mg

. (1.94)

Starting from the elements, we can reach the assemblage forsterite + pyrope at an arbitrary

temperature T (and P = 1 bar) by either (1) forming forsterite + pyrope at 298 K and then

heating this assemblage to T, or (2) forming spinel + 2 enstatite at 298 K, heating this

assemblage to T, and then reacting it to form forsterite + pyrope (Fig. 1.10). The enthalpy

54 Energy in planetary processes

5Mg+2Al

+4Si+8O

1 bar, 298.15 K

Fo + Prp

1 bar, 298.15 K

1 bar, T

(

1, 298

)

1, 298

)

Prp

1, T

Fo + Prp

298

P, Fo

P,Prp

] d

Sp + 2 En

1 bar, 298.15 K

Sp + 2 En

1bar,T

298

P, Sp

+2C

P,En

] dT

(

1, 298

)

+2(

1, 298

)

Fig. 1.10

Enthalpy of the reaction spinel + 4 estatite →forsterite + pyrope, at T and 1 bar.

change along the first path is:

H





1,298



prp





1,298





298

P,prp

dT +



298

P, fo

dT (1.95)

and along the second path (note the explicit stoichiometric coefficient of enstatite):

H





1,298







1,298





298

P,sp

dT +2



298

P ,en

dT +

1,T

(1.96)

As enthalpy is a state variable, H

=H

, so:



H =





1,298



prp





1,298





298

P,prp

dT +



298

P, fo

−







1,298







1,298





298

P,sp

dT +2



298

P,en



(1.97)

Let us now introduce some additional notation that will simplify this equation. The sum of

the four enthalpies of formation is simply the enthalpy of reaction at 298 K and 1 bar. Let

us call this sum 

1,298



1,298





1,298



prp





1,298



−







1,298







1,298





(1.98)

Because all the integrals are evaluated over the same temperature interval we can also

collect all the heat capacity functions (assuming that they are all described by the same

function) in a single function, which we call 



P,prp

P,fo

−



P,sp

+2C

P,en



. (1.99)

55 1.14 Internal energy

Finally, we call the enthalpy of reaction at the temperature and pressure of interest 

P,T

In this case P = 1 bar, so our equation for 

1,T

becomes:



1,T

=

1,298



298



dT . (1.100)

This equation is completely general. It applies to any chemical reaction, as long as there are

no phase transitions along any of the paths. If phase transitions occur then their enthalpies are

simply added separately, as was done with H

freezing

in equation (1.93), which is otherwise

identical to (1.100). These calculations will very quickly become second nature and you will

be able to do away with the diagrams. When in doubt, however, sketching diagrams such

as Figs. 1.9 and 1.10 will always point you to the correct result. Simple Maple procedures

to carry out the numerical calculations are described in Software Box 1.1.

Calculating the effect of pressure on 

H is less straightforward than calculating theeffect

of temperature. This is so partly because the equation for (∂H /∂P )

is not a simple function

of other thermodynamic variables or material properties (compare to (∂H /∂T )

). The

partial derivative (∂H /∂P )

is a function of molar volume, so that integating H =H(P)

requires an EOS. These are different for gases and condensed phases, and we defer their

discussion to later chapters.

1.14 Internal energy and the relationship between macroscopic

thermodynamics and the microscopic world

The internal energy of a system is the sum of energy contributions from translation, rotation

and vibration of molecules, their electronic configurations, their nuclear configurations,

and their electrostatic interactions (i.e. chemical bonding). If we do not consider nuclear

reactions, including radioactive decay, then the nuclear contribution to E stays constant.

If we also exclude chemical reactions and excitation of electronic shells by high-energy

electromagnetic radiation then the electronic and electrostatic contributions to E also stay

constant. With these restrictions, changes in E arise from changes in the translational, rota-

tional and vibrational energies of the molecules, in response to changes in the macroscopic

variables temperature and pressure. We seek a mathematical relationship between internal

energy and temperature as a first step towards understanding some of the ways in which the

macroscopic language of thermodynamics reflects processes that take place at the micro-

scopic scale. A simple derivation which relies on classical deterministic physics, called the

kinetic theory of gases, has been known since the mid nineteenth century. The kinetic theory

of gases is only applicable to the simplest of systems: a gas made up of non-interacting

particles, i.e. an ideal gas. For all other systems, the link between phenomenological ther-

modynamics and microscopic processes can only be constructed on the basis of statistical

mechanics and must include considerations of quantum mechanics as well. This is beyond

the scope of this book.

1.14.1 Internal energy of a monatomic ideal gas

Consider a gas made up of non-interacting point-like particles, i.e. a monatomic ideal gas.

In such a substance, the only possible kind of energy that can exist at the microscopic level

56 Energy in planetary processes

is the kinetic energy of motion, or translation, of the particles. The internal energy of such

a gas must therefore be equal to the sum of the translational kinetic energies of all of the

particles that make up the gas. In this case the link between the macroscopic state variable

E and the microscopic repository of energy admits no other possible interpretation, because

of the restrictions that we have imposed on the nature of the substance: non-interacting,

point-like particles.

Not all particles have the same kinetic energy. As we saw in Section 1.4.2, molecular

speeds follow a statistical distribution known as the Maxwell–Boltzmann distribution (Fig.

1.4). A consequence of this distribution of molecular speeds is that if a gas is at equilibrium

at a given pressure and temperature, then the average kinetic energy of the particles, U

,

is a well defined and unique value. This is the microscopic reason why E is a state variable.

The molar internal energy is then given by:

E =NU

=N

mc

, (1.101)

where N is Avogadro’s number, m is the particle mass and c

 is the mean-square particle

speed. This is not the square of the mean, but the mean of the squares. The reason for this

is that we are averaging kinetic energy, which scales as the square of the speed.

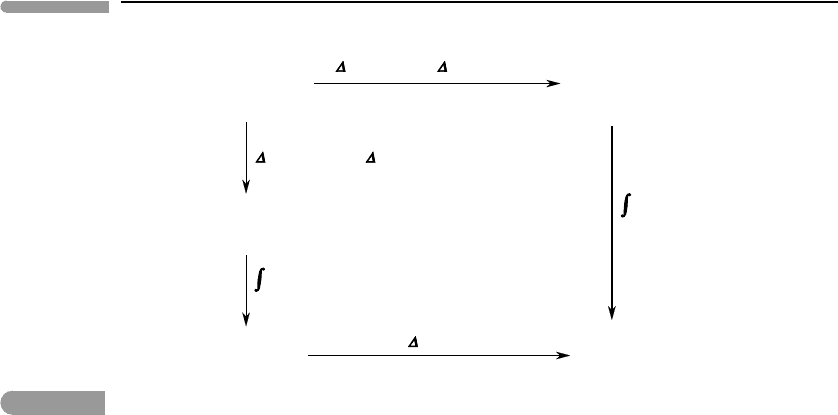
The velocity of each particle can be written in terms of three independent components:

, c

along three orthogonal directions (Fig. 1.11) such that:

. (1.102)

Now, by symmetry, it must be:

c

=c

=u

 (1.103)

so that:

c

=3u

. (1.104)

Fig. 1.11

Translational degrees of freedom of a particle.

57 1.14 Internal energy

This result also arises from Maxwell’s principle of equipartition of energy. What the prin-

ciple states is that, in a collection of particles, energy is distributed evenly among all of the

degrees of freedom of the particles. By degrees of freedom we mean, in general, variables

that can vary independently of one another. We will come across different ways in which

this terminology is used, and the actual meaning will in every case be explained and then

become obvious from the context. When studying the behavior of particles in a micro-

scopic system, by degrees of freedom we mean independent ways in which particles can

carry energy. If particles only have translational kinetic energy, then they have three degrees

of freedom, corresponding to the three perpendicular directions in which they can move.

The principle of equipartition of energy then says that the average kinetic energy along each

of the three directions must be the same, for if particles are moving more slowly in one of

the three directions then collisions will eventually increase their speed in that direction at

the expense of the speed (=kinetic energy) in the other directions. This intuitive explana-

tion makes sense, but it does not prove the validity of the principle. Equipartition of energy

remains a principle, i.e. a statement whose truth is assumed a priori, and that is accepted

because it leads to results that agree with observations. The same is true, of course, of the

laws of thermodynamics, the principle of conservation of momentum, and all other physical

laws and principles.

Because of the principle of equipartition of energy, we can use equation (1.104) in order

to re-write equation (1.101) as follows:

E =

Nmu

. (1.105)

This equation says that the average kinetic energy of the particles for each degree of freedom

mu

, and the internal energy, which equals the total kinetic energy of the particles,

equals this energy times three (one for each degree of freedom) times the total number of

particles.

We know that internal energy is a function of temperature and we want to find out what

this function is on the basis of the microscopic description of the system. It is a remarkable

fact that this is in principle always possible, no matter how complicated the system may be.

The formal method for doing this relies on finding a fundamental function that is defined

in statistical mechanics and is called the partition function (see, for example, the textbooks

by Hill, 1986, or Glazer & Wark, 2001).

All thermodynamic state variables can be derived from a substance’s partition function.

The problem is that it is seldom easy to find what the partition function for a given substance

is. For the simplest of cases, ideal gases, it is possible to derive the value of the state functions

both from the partition function and from the much simpler formalism of kinetic theory, as

we do here. This is not true in general, though.

We begin by working out an expression for the pressure of an ideal gas, which must arise

from collisions of the particles against the walls of the container. Pressure is force per unit

area, and we recall from elementary physics (Newton’s second law of motion) that force

equals the rate of change of momentum. We assume that the particles that make up the ideal

gas are perfectly elastic. Therefore, when a particle collides with a surface perpendicular to

any one of the three independent directions of translation it reverses direction but does not

lose speed, so that its momentum changes by:

mu −

(

−mu

)

=2mu. (1.106)