Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

28 Energy in planetary processes

where /

is a constant called the permittivity of free space (Appendix 1), and the SI unit

of charge is the coulomb, symbolized C. The intensity of the electric field, E, is the force

exerted per unit of charge (e.g. in units of N C

−1

). For a point charge of magnitude q in

vacuum it is given by:

E =

4π/

. (1.39)

Coulomb’s law is formally identical to Newton’s law of gravitation. For instance, compare

the equations for the gravitational and electric field intensities, g and E (1.7) and (1.39).

Both field intensities decrease with the square of distance, and both are proportional to the

magnitudes of the property that generates the field (mass or electrical charge). A crucial

difference between the two physical laws is that gravity is always attractive, whereas elec-

trostatic force can be attractive or repulsive, depending on whether the charges are different

or alike, respectively. This is the reason why equation (1.38) uses the absolute value of

the charges, |q|, whereas no such specification is needed in Newton’s law of gravitation.

Another important difference is that all materials behave identically relative to gravity, so

that the universal gravitation constant, G, is unique. In contrast, different materials behave

differently in the presence of an electric charge, so that if the charges are separated by any

medium other than vacuum the constant /

must be replaced by /, the permittivity of the

material in question. For all materials, />/

, so that the force between electric charges is

maximum in vacuum.

Electrostatic and gravitational forces are also of vastly different magnitudes, as we

mentioned in the previous section. We quantify this statement in the following Worked

Example.

Worked Example 1.4 Relative magnitudes of gravitational and electrostatic forces

Let us compare the relative strengths of gravitational and electrostatic forces at atomic length

scales and planetary length scales. From Newton’s law, equation (1.2), and Coulomb’s law,

equation (1.38), we derive the ratio of the gravitational force |

| to the electrostatic force

| between two bodies with masses m

and m

, carrying electric charges q

and q

and

immersed in a medium of permittivity /:

=4π/G

||q

. (1.40)

Because gravitational and electrostatic forces are both described by inverse square laws this

ratio is independent of the separation between the objects. It depends only on their mass to

charge ratio and on the permittivity of the surrounding medium. Given that electrons are the

smallest stable charged particles (they carry the unit of electric charge) we can use the mass

and charge of the electron to get an idea of the intrinsic difference between gravitational

and electric forces. Substituting the appropriate values for the electron (Appendix 1), and

taking / =/

(i.e. electrons in vacuum), we find:





electron

≈2.4 ×10

−43

. (1.41)

29 1.8 Energy associated with electric and magnetic ﬁelds

In other words, gravity is some 42 orders of magnitude weaker than the electrostatic force!

A major unsolved problem of physics is why this difference is so vast (see, for example,

Randall, 2007). As planetary scientists, we can use this result to reassure ourselves that

when we study planetary systems and materials at the microscopic level we can neglect

gravity.

But if gravity is so much weaker than electrostatic forces, then under what conditions

does gravity become the dominant force? Let us consider two bodies of identical mass,

m, carrying identical charges, q, and immersed in a medium of permittivity /. We make

|=|

| and we obtain from equation (1.40):

q =

(

4π/G

)

1/2

m. (1.42)

We seek an estimate of the characteristic size, λ, of a particle for which this equality is likely

to be satisfied. For particle diameters greater than λ gravity will prevail over electrostatic

forces (although of course the size has to be considerably greater than λ for the difference

to be significant). Let each of the bodies be a sphere of radius λ and density ρ. The mass of

each sphere is given by:

m =

πλ

ρ. (1.43)

The dielectric strength of a material is defined as the intensity of the electric field, E, under

which the material breaks down and starts conducting electricity. For example, lightning

occurs when the dielectric strength of air is exceeded. In our example, the dielectric strength

of the medium separating the spheres is what controls the maximum amount of charge that

can be stored in them. We next state without demonstration the following relationship

between the electric charge q in a sphere of radius λ and the intensity of the electric field,

E, at the surface of the sphere

E =

4π/λ

. (1.44)

This result follows from a theorem of vector calculus known as Gauss’s theorem (see, for

example, Sokolnikoff & Redheffer, 1966, p. 397). It says that the charge behaves as if it

were concentrated in the center of the sphere (compare equation (1.39)). The electric field

is maximum at the surface of the sphere and falls off away from it following the inverse

square law. If the sphere is immersed in a medium of dielectric strength k

, then it can

sustain a maximum electric field E = k

, and can thus store a maximum q of:

q = 4π/λ

. (1.45)

Substituting equations (1.43) and (1.45) in equation (1.42) and solving for λ:

λ =

(

4π/G

)

1/2

. (1.46)

Let us assume that the medium separating the spheres is a gas at low pressure ≤ 1 bar.

The permittivity of gases at low pressure does not differ significantly from the permit-

tivity of vacuum, so we make / = /

. Air at 1 bar has a dielectric strength k

≈ 3

× 10

−1

. This value decreases with decreasing pressure, attains a minimum at

30 Energy in planetary processes

pressures of about 0.01 bar, and then increases again approaching a value of ∼ 10

−1

for very rarerified gases, such as those in interplanetary space (see, for example,

https://commons.lbl.gov/display/ALSBL6/Dielectric+strength+of+air).Taking a character-

istic value of ρ for rocks of 3000 kg m

−3

, we get values for λ ranging from 300 m for air at

1 bar to 100 km for the interplanetary medium. In between, there is a range of gas pressures

(≈ 0.01 bar) for which λ becomes very small, perhaps of the order of millimeters.

These numbers mean that for planetary bodies larger than about 100 km electrostatic

forces can never be greater than gravitational forces, because the charges that would be

required to produce such forces would be dissipated in electrical discharges. For rock bod-

ies in an atmosphere such as Earth’s, the calculated size limit is about 300 m. In practice

the crossover lengths must be much smaller than these, perhaps by several orders of mag-

nitude, because even if the dielectric strength of the medium is not approached there are

few processes in planetary environments that can generate electrical charges of the high

magnitudes that would be required to compete with gravitational forces.

1.8.2 Atomic bonding

Electrostatic forces are responsible for atomic bonding. Charged particles in an electrostatic

field have electrostatic potential energy, U

, which accounts for interaction between two

oppositely charge particles separated by a distance r in vacuum that we write as:

4π/

. (1.47)

This equation is analogous to (1.6), for gravitational potential energy. As in that case we

set U

= 0 at infinity, but the sign convention is opposite to that of gravitational potential.

This is convenient because electrostatic forces can be both attractive and repulsive (e.g.,

Griffiths, 1999, p. 90–96), but it makes no difference for the present discussion.

In an ionic compound, such as the mineral halite, the crystalline structure is held together

by electrostatic attraction between oppositely charged ions. The lattice energy of an ionic

crystal is defined as the energy released when the free ions in a gas phase come together to

form the solid (e.g., Holbrook et al., 1990). By “free ions” we mean an ideal situation in

which the ions are infinitely distant in vacuum. If only one ion each of sodium and chloride

were involved, the lattice energy of sodium chloride would be the electrostatic potential

energy U

(given by equation (1.47)) for a Cl

−

anion and a Na

cation separated by the

interatomic distance in halite, r. Note that because the ions have opposite charges U

< 0.

This is the amount of electrostatic potential energy that was “lost” when the ions moved

from infinity (U

= 0) to their equilibrium position. Of course, the energy is not lost but

converted to some other type of energy. In this case, the electrostatic potential energy of ions,

which is a microscopic property of the system, is dissipated as heat when the crystal forms.

This heat is what we call the lattice energy of the crystal, which is a macroscopic property.

In practice, a calculation based on equation (1.47) does not yield the correct value of

lattice energy because one must consider not just the force between individual ions (or, in

the language of physics, point charges) but rather interactions among electrostatic fields

arising from a distribution of point charges. Each anion and cation in the structure of halite

interacts electrostatically not just with one nearest neighbor of the opposite charge, but with

many ions of both equal and opposite charges, located at different distances. If the crystalline

31 1.8 Energy associated with electric and magnetic ﬁelds

600 700

- J per molecule

800 900 100

–10

–8*10

–6*10

–19

–18

Melting point at 1 bar - °C

NaBr

NaI

KCl

RbF

RbBr

RbI

CsF

CsCl

CsBr

CsI

NaCl

KBr

RbCl

NaF

Fig. 1.5

Correlation of single-pair interatomic electrostatic potential energies (U

) with melting points of alkali halides

(melting points from CRC Handbook of Chemistry and Physics).

structure of an ionic compound is well known, then its lattice energy can be calculated on the

basis of equation (1.47) and a set of geometric parameters known as Madelung constants,

that account for interactions among distant ions (see Moody & Thomas, 1965). A simpler

approach is Kapustinskii’s equation (Kapustinskii, 1956; Moody & Thomas, 1965), which

is based on equation (1.47) and a single constant that depends on the number of atoms

per formula unit and that essentially sums up the contributions of all significant Madelung

constants. Both of these approaches entail the calculation of a macroscopic property, the

lattice energy, from considerations of the microscopic structure of the system.

Even if equation (1.47) does not yield exact lattice energy values, the general validity of

this discussion can be gauged by comparing values of U

calculated with equation (1.47)

to the melting points of simple ionic compounds (Fig. 1.5). As anions and cations get larger,

the value of r increases and the absolute value of U

decreases. For example, given that

ionic radii of both halogens and alkali metals increase with increasing atomic number, the

electrostatic potential energy calculated with equation (1.47) should become a negative

number of smaller absolute magnitude for alkali halides of progressively higher atomic

number combinations. NaF has the shortest atomic bond among all the halides shown in

Fig. 1.5, so that its formation releases the greater amount of electrostatic potential energy.

NaF should thus have the strongest atomic bond, or, in other words, the highest melting

point. This is indeed the case (Fig 1.5). Melting points are negatively correlated with U

as we should expect from the fact that formation of shorter bonds releases a greater amount

of electrostatic potential energy, so that they require higher energy to be broken.

Pure ionic compounds are rare among planetary materials. In particular, silicates contain

a complex and variable combination of covalent, ionic and van der Waal’s bonds. Definition

of lattice energy in such compounds is less straightforward (e.g. Glasser & Brooke Jenkins,

2000; Yoder & Flora, 2005), but chemical bonding in them is nonetheless a consequence of

32 Energy in planetary processes

the fact that, in order to break apart their crystalline structure, it is necessary to perform work

against electrostatic forces. Electrostatic forces are also responsible for the divergence of

the behavior of real gases from that predicted by the ideal gas EOS. For instance, real gases

are able to condense as liquids but ideal gases are not. Electrostatic forces are responsible

for this difference.

1.8.3 Magnetic forces

Coulomb’s law describes the force between static electric charges. If electric charges are in

motion, which is what we call an electric current, an additional force arises between moving

charges. This is what we observe as a magnetic force. The magnetic field generated by an

electric current is described by a mathematical equation known as Biot–Savart law, which is

more complicated than the equations that describe the gravitational and electrostatic fields.

I will not present this equation explicitly (see, for example, Griffiths, 1999), but I will state

two important properties of the magnetic field, symbolized by B. First, the intensity of the

field generated by a current flowing in an electrical conductor is directly proportional to the

intensity of the current (amount of charge moving per unit of time). Second, the orientation

of the magnetic field is perpendicular to the current direction.

Magnetic fields act only on moving electric charges. Stationary electric charges, or par-

ticles with no electric charge, do not interact with a magnetic field and are subject to no

magnetic force. A moving charge is subject to a magnetic force that has a magnitude pro-

portional to: the intensity of the magnetic field, the magnitude of the electric charge, and

the component of the charge’s velocity perpendicular to the field. The magnetic force,

described mathematically by the Lorentz force law, is oriented perpendicular to the direc-

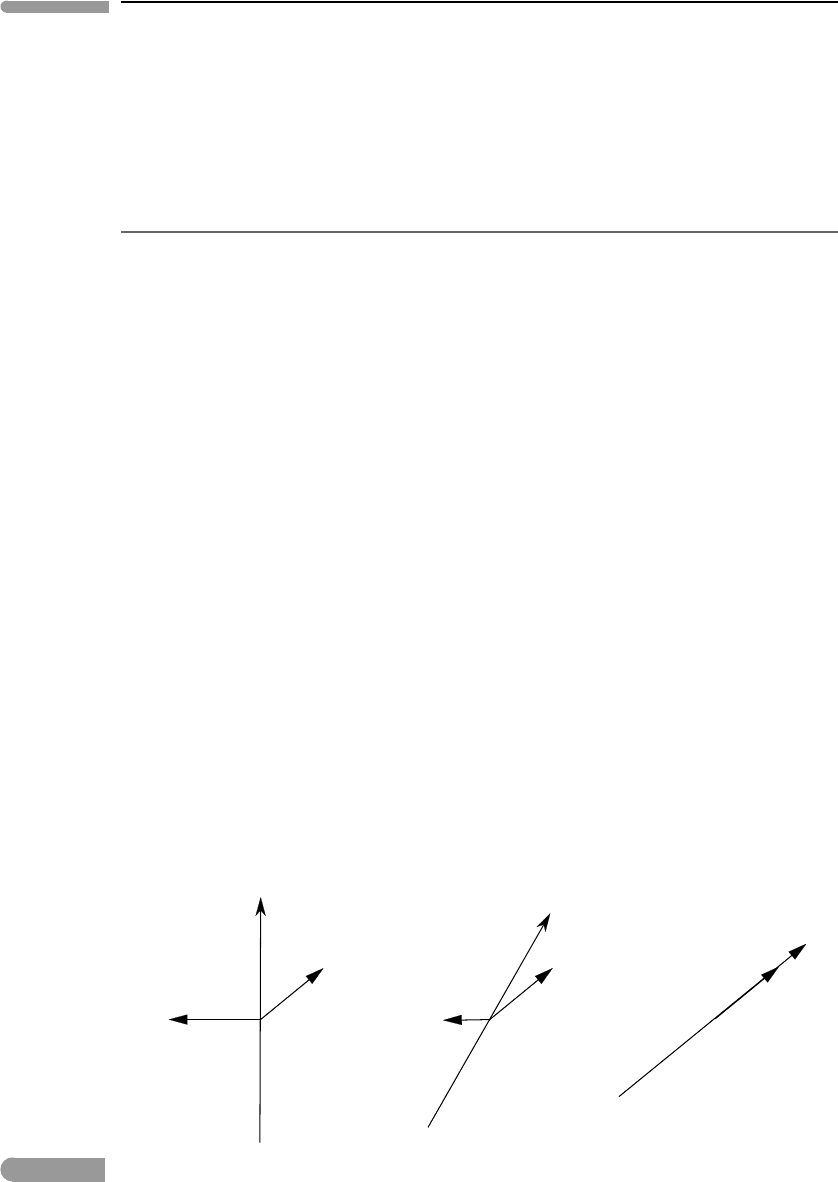
tion of motion of the charge, i.e. the current direction (Fig. 1.6). If a charged particle moves

in a direction parallel to that of the magnetic field then there is no magnetic force.

Because of the way in which magnetic forces act on moving charges, a stationary magnetic

field (one that does not change, in intensity nor orientation with time) performs no work. This

is so because the magnetic force is always perpendicular to the displacement of the particles

that feel the force (Box 1.1). In principle, then, no energy would appear to be required in

order to maintain a magnetic field, but there are some hidden liabilities here. In the first

place, the magnetic field exists as a result of an electric current and all electrical conductors

Fig. 1.6

Relationship between the magnetic ﬁeld, B, the electric current, I, and the Lorentz force, F

. When B and I are parallel

=0.

33 1.8 Energy associated with electric and magnetic ﬁelds

have a finite resistance that dissipates some of the electrical energy in the current (kinetic

energy of moving charges). This particular type of energy conversion (electrical energy to

heat) is called ohmic heating (because Ohm’s law relates current intensity and electrical

resistance to energy dissipation). Sustaining a magnetic field requires a constant supply

of electrical energy that is dissipated as heat. Secondly, the Lorentz force is perpendicular

to the direction of motion of charges (a microscopic concept) but not necessarily to the

direction of motion of macroscopic parcels of the conductor that carries the charges. If the

conductor moves in response to the Lorentz force then work is certainly being performed.

The energy must come from the electric current that generates the magnetic field, i.e. the

intensity of the current must increase in order to balance the work performed by the Lorentz

force. The magnetic field acts as a transfer medium for this energy.

All planets in the Solar System with the exception of Venus and Mars have magnetic

fields (Pluto is not a planet). Even if a planetary magnetic field performed no work, and

as we shall see this is not the case, its existence implies that there must be a source of

energy that generates the electric current responsible for the magnetic field, and that at least

some of this energy is dissipated by ohmic heating. There are good reasons to hypothesize

that the origin of planetary magnetic fields is circulation of electrical currents in the deep

interiors of the planets, and that the currents are generated by a process that is described as

a self-excited planetary dynamo (Bullard & Gellman, 1954). The details of this process are

fiendishly complex and a full discussion is beyond the scope of this book – see for example

Buffett and Bloxham (2002), Jones et al.(1995), Kuang and Bloxham (1997), Olson et al.

(1999).

The existence of planetary dynamos is based on the fact that there is an inverse to Biot–

Savart law: if a material that contains free electric charges (e.g. electrons in an electrical

conductor) moves in a magnetic field, then an electric current will flow in the conductor,

with an intensity proportional to the intensity of the magnetic field. The energy that appears

as electrical energy does not come from the magnetic field, but from whatever is the source

of the force that moves the conductor in the magnetic field. The explanation for planetary

magnetic fields is that electrical conductors move in the planet’s magnetic field, inducing

electric currents which in turn generate the magnetic field – hence the term “self-excited”.

The nature of the electrical conductor varies among different planets. It is likely to be

molten metal in the Earth’s core, pressure-ionized hydrogen in Jupiter and Saturn and

electrolyte-rich aqueous solutions in Uranus and Neptune.

Planetary dynamos would come to a stop, and planetary magnetic fields would collapse,

in the absence of an energy source that keeps the electrical conductor moving. That energy

source is heat, so we must look for processes that can convert thermal energy to mechanical

energy. One such process, and the one that is thought to be responsible for planetary magnetic

fields, is thermal convection. We discuss convection in Chapters 3 and 4. For now we

notice that one of the outcomes of convection is to transform thermal energy to kinetic

energy. In an electrically conductive layer, such as the Earth’s core, this kinetic energy is

dissipated by a combination of processes (Fig. 1.7). Some of it is dissipated as heat by

friction in the convecting medium – this process is called viscous heating and occurs in

any convecting material, whether or not it is electrically conductive. The rest of the kinetic

energy is converted to electric current (i.e. electric energy) and some of it is dissipated by

ohmic heating. The intensity of the current, and hence the rate of conversion of kinetic

energy that is required to sustain it, is a function of the magnitude of the work performed

by Lorentz forces. Some of this work is performed by the planet’s magnetic field outside

of the electrically conductive layer in which the magnetic field is generated, and dissipates

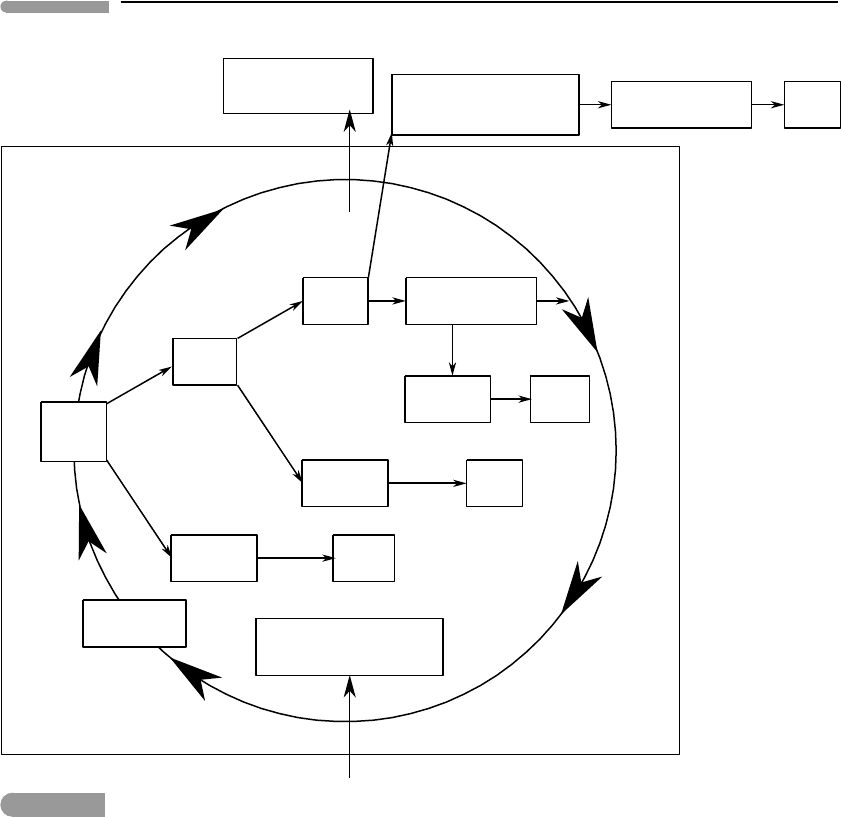
34 Energy in planetary processes

convection

viscous

dissipation

Viscous

electric

current

ohmic

dissipation

Ohmic

Lorentz

force

Lorentz work on

convecting fluid

Lorentz work on

atmospheric and

interplanetary media

viscous & ohmic

dissipation

Space

viscous

dissipation

Lorentz

: crystallization,

radioactive decay,U

out

to overlying layer

Fig. 1.7

The energetics of planetary magnetic ﬁelds. The box is the conductive layer in which the ﬁeld is generated. The layer

absorbs thermal energy (Q

) from sources such as crystallization and radioactive decay, and expels thermal energy

out

) to the overlying cooler environment. U

is kinetic energy of the moving conductor. This energy is dissipated by

viscous and ohmic heating both within the convective layer and outside of it.

energy, for instance, by heating of conductive plasma in the planet’s atmosphere or in the

interplanetary environment. The fraction of energy that is dissipated in this way is probably

negligible. Most of the work done by Lorentz forces translates to motion of the conductive

material that generates the magnetic field and is ultimately dissipated by viscous heating.

Suppose that no energy is dissipated externally to the layer in which the magnetic field

originates, i.e. we somehow manage to eliminate viscous and ohmic heating in the atmo-

sphere and space environment (see Fig. 1.7). Then a combination of viscous and ohmic

dissipation would return all the kinetic energy of convection as heat to the same thermal

reservoir from which heat was derived to drive convection in the first place. This mecha-

nism would appear to be capable of operating indefinitely without influx of energy. There is

nothing in the law of conservation of energy that would prevent it. And yet such a perpetual

35 1.9 Thermal energy and heat capacity

motion machine is impossible. The Second Law of Thermodynamics requires a thermal

gradient in order for conversion of heat to mechanical energy to take place, which means

that the convective layer must lose heat to its environment, or convection will stop.

1.9 Thermal energy and heat capacity

Heat and thermal energy are not the same. The relationship between the two concepts

parallels that between mechanical energy and work. Heat is a quantity that measures the

exchange of thermal energy between systems, or parts of a system, that are at different

temperatures. I have taken for granted that thermal energy, and heat, are equivalent to other

types of energy, and that they are measured in the same units (Joules in the SI system). The

validity of this statement is not evident a priori, and is based on experimental observations,

beginning with those of James P. Joule in the mid nineteenth century.

Given that heat flows down a temperature gradient, and that heat flow is a transfer of

thermal energy, it follows that temperature is an indicator of the thermal energy content of

a system. It is important to emphasize: temperature is not energy, but it must vary directly

with thermal energy content. A somewhat imperfect analogy is the position of a body in

a gravitational field, e.g. elevation above the surface of a planet. Elevation is not energy,

but it is related in a direct way to potential energy (equation (1.6)). Left alone, a body will

fall to a lower elevation and transfer potential energy, via work of the gravitational force,

to kinetic energy. A body at high temperature relative to another one will transfer thermal

energy to the latter, via heat flow.

Quantifying the relationship between temperature and thermal energy begins with the

definition of heat capacity, symbolized by C. The heat capacity of a system is the ratio

of the heat absorbed by the system to its temperature increase. Because heat capacity is

generally not a constant, the definition is cast in differential form, i.e.:

C =

, (1.48)

where dQ symbolizes heat absorbed by the system. The sign convention is important and

must be emphasized: dQ > 0 means that the system absorbs heat. Heat capacity is therefore

always a positive quantity. Definition (1.48) is incomplete, because, unless one precisely

specifies under what conditions heat transfer takes place, the value of C is not well defined.

Consider a system made up of a fixed amount of liquid water. If the system absorbs the same

amount of heat at constant volume (e.g. the water is held in a perfectly rigid container) and

at constant pressure (the container is perfectly flexible and transmits atmospheric pressure),

the temperature increase will be greater in the former case than in the latter. This is so

because, if the volume is not allowed to change, then all the heat becomes thermal energy.

On the other hand, volume increases at constant pressure, so that some of the heat becomes

expansion work. In this case the increase in thermal energy, and hence in temperature, will

be less than in the constant volume case. Consider now the same system in the flexible

container but at the liquid–gas phase transition temperature (i.e. the boiling point of water).

As long as both a liquid and a gas phase are present, the heat capacity is infinite, for in this

case dT = 0 for finite values of dQ.

We must specify the exact conditions under which the heat transfer process takes place.

This applies to all thermodynamic processes, and is known as imposing constraints.A

36 Energy in planetary processes

possible constraint is that no work be performed during heat transfer, so that all heat becomes

thermal energy. We symbolize the no work constraint with the subindex {W}, so that:

{W }





{W }

(1.49)

means heat capacity measured under conditions such that no work is performed. If the only

kind of work that we are concerned with is expansion work then the constraint {W }becomes

simply a constant volume condition (equation (1.19)). We define the constant volume heat

capacity for a homogeneous system as follows:





. (1.50)

If the system is able to perform other types of work, such as gravitational or electrostatic

work, elastic shear work or work by a Lorentz force in a magnetic field, then the {W }

constraint must be defined differently.

If a system absorbs heat under conditions such that no work is performed then its energy

content must increase by an amount equal to the heat absorbed. This energy content is

measured by the thermodynamic state variable (or state function) internal energy, which

we will symbolize by E (this symbol is not universally used; some authors use U for

internal energy but I reserve U for various types of mechanical energy). The meaning of

state variable is that, as long as a system is at equilibrium, the value of the variable depends

only on the state of the system (as defined, for example, by its pressure and temperature)

and not on the path that the system followed to reach that state. In other words, given P

and T, the value of the internal energy of a system at equilibrium is unique. State variables

preserve no memory of the system’s history.

Internal energy, as all other thermodynamic state variables, is a macroscopic property. Its

physical interpretation requires that we discuss the system from a microscopic point of view

(Section 1.14), but its macroscopic definition is simple and follows from equation (1.50).

For systems for which the only possible type of work is expansion work, and in which no

phase transitions nor chemical reactions take place, the heat exchanged at constant volume

must be equal to the change in internal energy, so we can rewrite equation (1.50) as follows:



∂E

∂T



. (1.51)

This equation can be taken as the definition of either internal energy or constant volume

heat capacity. Which of the two we choose is not important. What matters is that it allows

us to calculate things – this is the essence of what an operational definition is. Note that this

is the definition of internal energy only if expansion work is the only possible type of work

for the system of interest. If other types of work are possible, then the general definition of

internal energy is the following:

{W }



∂E

∂T



{W }

. (1.52)

The derivative symbols in equation (1.50) have become partial derivative symbols in

equations (1.51) and (1.52). This is so because E is a state function whose value is fixed by

the values of the independent variables that define the state of the system. In other words,

E is a function of several variables (see Box 1.3) and the notation in equation (1.51)is

37 1.9 Thermal energy and heat capacity

an unambiguous indication: (i) that the two independent variables that we are using in this

particular case to define the state of the system are temperature and volume, and (ii) that

we want to measure the rate of change in internal energy with respect to temperature while

holding the system’s volume constant. Volume is the only variable that is constrained to be

constant. Other variables, such as pressure, vary during constant volume heating, but the

energetic consequences of changes in these other variables are implicitly built into equation

(1.51) (see also Box 1.4).

Box 1.4

Comments on the notation of thermodynamics

It has been pointed out that the notation:



∂y

∂x



(1.4.1)

is unique to thermodynamics and is at odds with standard mathematical usage. Some authors (for

example, Truesdell, 1984) have called for the abolition of this supposed abomination, and a recasting of

thermodynamics in standard mathematical notation. This would be desirable from a formal point of view,

but in my opinion it ignores the physical essence of thermodynamics, or at least of its practical applications.

Although the state of a system is deﬁned by the values of only a few intensive variables (at least two) there

are other quantities that do not vary independently.

Say that y = y(x, z) is a state function. Geometrically this is a two-dimensional surface that exists in a

space of at least three dimensions. In thermodynamics the number of dimensions of the embedding space

is always more than three, meaning that y is a function not only of x and z, but also of other variables, u,

v, w, etc. But once we specify that we are interested in the behavior of y as a function of x and z we lose

the freedom to choose the values of these other variables – they are determined by the intersection of the

y surface with the corresponding coordinates. The surface y = y(x, z) is only one of many possible surfaces

that determine the value of y. We could also have chosen y = y(

v,w), and then the values of x and z

would be ﬁxed by the intersections of this other surface. The expression:

dy =



∂y

∂x



dx +



∂y

∂z



dz (1.4.2)

tells us unequivocally which is the particular y surface that we are considering. The advantages of

thermodynamics’s peculiar notation will become clear in subsequent chapters.

The partial derivative notation was not used in equation (1.50) because Q is not neces-

sarily a function of any other variable. In fact, an equation such as (1.50) is mathematically

sloppy, though useful from a physical point of view. All this equation is saying is that we

want to track how absorption of an infinitesimal amount of heat changes the temperature

of a system, even if in general there is no function Q = Q(T,V) that we can differentiate

to obtain C

. This is not true of state variables: the function E = E(T,V) exists and is

differentiable. This distinction is commonly formulated as one between exact and inexact

differentials. The derivatives of state variables are exact differentials, which means that the

values of state variables are given by differentiable functions. In contrast, dQ and dW are

inexact differentials: they represent infinitesimal amounts of heat transferred or work per-

formed, but there may not exist a function of other thermodynamic variables that may allow

us to calculate derivatives of Q and W. A corollary of this statement is that Q and W cannot