Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

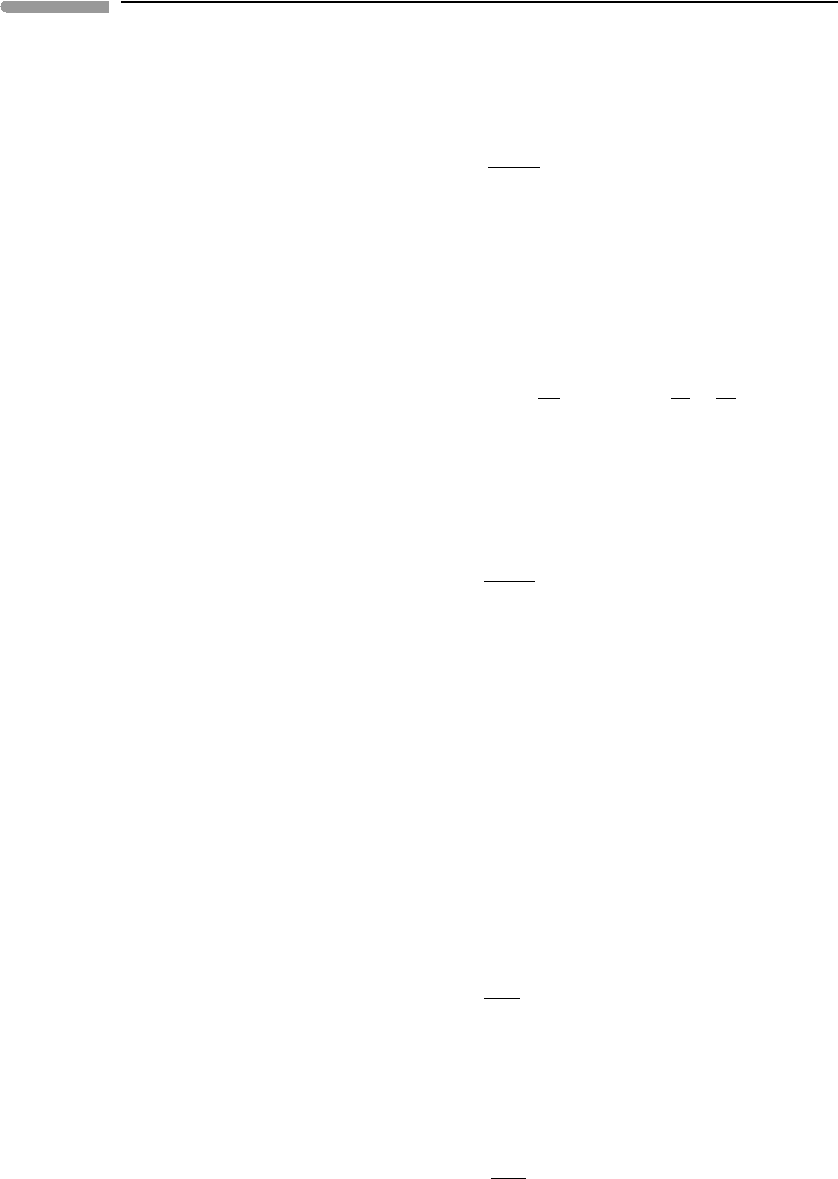
8 Energy in planetary processes

then

always has a negative orientation – this is the mathematical expression of the fact that

gravity is always an attractive force. We can then write the inner product in equation (1.3)

as:

·d

x =−

GMm

dx, (1.4)

where the negative sign arises from the fact that we are calculating the inner product

between a vector and a one-form that subtend an angle of 180

◦

(Box 1.1). This is the work

performed by the gravitational force (the general three-dimensional case requires more

complex notation, but the physics are well summarized in (1.4)). The change in gravitational

potential energy that corresponds to a finite displacement between two positions, x

and x

can be obtained by substituting (1.4) into (1.3) and integrating:

g,b

−U

g,a

=−



·d

x = GMm



=−GMm



−



. (1.5)

By convention, we define gravitational potential energy as being 0 when the objects are

separated by an infinite distance, i.e. we make U

g,a

=0asx

→∞. With this convention we

then define the gravitational potential energy of an object with mass m in the gravitational

field of a planet with mass M as:

=−

GMm

, (1.6)

where r is the distance between the centers of mass of the two bodies. For any finite value

of r, U

is negative, and U

approaches a maximum value of 0 as the separation between

the two bodies approaches infinity. When writing equation (1.4) I justified the negative

sign on purely mathematical grounds, as arising from the inner product of two oppositely

pointing vectors, but we can now see the physical meaning of this negative sign. Suppose

mass m is moved away from M (r > 0). In order for this to occur an external agent must

perform work. By conservation of energy this work becomes stored as potential energy in

the gravitational field. Therefore it must be U

> 0, which is what results from equation

(1.6) with r > 0. Conversely, if r < 0 the gravitational field gives up energy (U

< 0)

which is transferred to mass m and appears, for example, as kinetic energy.

I will introduce here two other equations that we use in the analysis of gravitationally

driven planetary heating in Chapter 2. First, we can see from equation (1.2) that the gravi-

tational acceleration, g, due to a body of mass M at a distance r from its center of mass is

given by:

g =−

, (1.7)

where the negative sign expresses the fact that gravitational acceleration is always attractive

(directed towards the mass that causes it, where r is positive away from the mass). Recall

that the numerical value of g is the intensity of the gravitational field. We also define the

gravitational potential, Φ

, as the gravitational potential energy per unit mass:

=−

. (1.8)

9 1.3 Mechanical energy

Gravitational potential is a scalar field (Box 1.1). Gravitational acceleration is a one-form

(or covariant vector) that is the gradient of the potential field. The magnitude of the one-form

is given by:

g =−

dΦ

. (1.9)

Force is another one-form, that is the product of a scalar (mass) times acceleration (Newton’s

second law of motion). Mass, or inertia, is the scaling factor between force and acceleration;

this is the origin of the term scalar.

We are generally concerned with differences in gravitational potential energy between

different states of a system. For example, when tectonic processes elevate a mountain range,

or when lava flows build a volcano, gravitational potential energy is stored in the rocks.

How much potential energy is stored in a mountain range? This depends on the distance

that the rocks can move towards the center of the planet before they get to a level below

which they can move no further. How do we define such a level? Sea level may be a

good first approximation, but we can give a more general answer, that will also hold for

planets without oceans. We begin by looking at two additional questions. First, where did

this gravitational potential energy associated with topography come from? Conservation of

energy requires that we identify an energy source, which in this case entails conversion of

some of the planet’s internal heat to gravitational potential energy (more on this in Chapter

3). Second, what happens to this potential energy as the mountain loses elevation? The short

answer is that this gravitational potential energy ultimately becomes heat and is dissipated to

space, but the pathway may entail some intermediate steps, depending on how the mountain

loses elevation. In general, elevation is lost by a combination of three processes: erosion,

isostatic adjustment and tectonic collapse. During erosion, potential energy becomes heat

as a result of friction during sediment transport and also when particles come to their

final resting place in a sedimentary basin. Isostatic adjustment may return gravitational

potential energy to the mantle, either as heat or as mechanical energy. Tectonic collapse

results in gravitational potential energy either being dissipated directly as heat during ductile

deformation, or being stored as elastic energy (another type of mechanical energy that we

will discuss) to be eventually dissipated, ultimately as heat too, during earthquakes. All of

these processes drive towards converting the surface of the planet to one over which there

are no differences in gravitational potential energy. Such a surface is called an equipotential

surface. Awell-defined reference level for potential energy on Earth is thus the geoid, which

is defined as the equipotential surface that is as close as possible (e.g. in a least square sense)

to mean sea level (see Worked Example 1.1). In planets without oceans, we may choose

as our reference the equipotential surface that is as close as possible to the mean planetary

radius (and, if we were to follow the same convention used for Earth, we should call such

surfaces: areoid, aphrodoid, hermoid, selenoid, etc.). We will generally be concerned with

differences between the value of U

at the geoid and its value at any other level that we

may be interested in.

Worked Example 1.1 Gravitational potential energy and topography

(a) Consider a mass m of rock initially located on Earth’s geoid. Let R be the geoid’s mean

radius. The rock is then moved to an elevation h above the geoid, such that h  R, i.e. we

stay close to the planet’s surface. The initial distance between the two centers of mass (the

10 Energy in planetary processes

rock’s and the Earth’s) is R, and the final distance, after the rock is raised, is R+h.We

first use equation (1.6) to show that the gravitational potential energy of the rock in its final

state, relative to the geoid, is given by mgh, the equation that you probably remember from

introductory physics.

Calling the gravitational potential energies at the geoid and at an elevation h above the

geoid U

g,geoid

and U

g,h

, we have:

g,h

−U

g,geoid

=−

GMm

R +h

−



−

GMm



GMmh

(

R +h

)

. (1.10)

If we stay close to the planet’s surface, then R(R+h) ≈R

. We can also consider the planet’s

gravitational acceleration to be constant over the interval R to R+h. Using equation (1.7)

to calculate gravitational acceleration at the geoid and substituting in (1.10):

g,h

−U

g,geoid

≈

GMmh

=−mgh =m|g|h. (1.11)

With our sign convention g is always a negative quantity. The “g”inmgh is thus the

magnitude of g, as shown in the last term of equation (1.11).

(b) The Sierra Nevada of California is the largest uninterrupted mountain range in the

United States. It is roughly 600 km long, 100 km wide and has a mean elevation of 1.5 km

(averaged over this horizontal extent). Assuming that this average elevation represents the

center of mass of the mountain range, and that the rocks making up the Sierra Nevada have

an average density of 2800 kg m

−3

, what is the potential energy stored in the Sierra Nevada

relative to the geoid? At the geoid, g ≈ 9.8ms

−2

. Plugging in these values into equation

(1.11) we find that the Sierra Nevada stores approximately 3.7 × 10

J of gravitational

potential energy, approximately equivalent to an explosive yield of one million megatons

(see Section 1.12.2).

constant rate of uplift over that time interval, the energy flux (energy per unit area per unit

time) that went into elevating the Sierra Nevada is approximately 3.9 ×10

−4

−2

0.39 mW m

−2

, where 1 W(Watt) = 1Js

−1

. Typical terrestrial heat fluxes are of the order

of 50–100 mW m

−2

, i.e. two orders of magnitude greater. There is plenty of energy in the

Earth to elevate mountain ranges.

1.3.2 Kinetic energy

Bodies in motion have kinetic energy, U

, that arises from their speed and is given by:

, (1.12)

where v is the magnitude of the body’s velocity, i.e. its speed. Kinetic energy is a function

of the relative speed between a body and an observer. For example, if we observe, from

a location at rest on the Earth, an asteroid of mass m moving towards Earth with speed

v, the kinetic energy of the asteroid in our reference frame is given by equation (1.12)

and the Earth has no kinetic energy in our reference frame. Measured from a reference

11 1.3 Mechanical energy

frame attached to the asteroid, on the other hand, the asteroid has no kinetic energy, and

the Earth has kinetic energy given by equation (1.12), but with m in this case being the

mass of the Earth. Although the two values of kinetic energy are very different, if the

two bodies collide the result is unique: conversion to heat of an amount of energy equiva-

lent to most of the kinetic energy of the asteroid, as measured from the Earth’s reference

frame (Worked Example 1.2). In order to see why this is the case we need to introduce

the law of conservation of momentum, which is a law of nature that, in classical physics,

is distinct from energy conservation. In reality, energy and momentum conservation are

different manifestations of a single conservation law that arises from the geometrical

properties of spacetime, but this becomes an issue only for objects moving at relativistic

speeds.

Momentum,

p, is a vector quantity, and is given by:

p = m ¯v, (1.13)

where ¯v is the velocity vector. The law of conservation of momentum states that the total

momentum of a system is conserved. In contrast to energy, that has many different mani-

festations, momentum is unique and is always conserved; it cannot be converted to other

“types” of momentum. In a perfectly elastic collision both momentum and kinetic energy

are conserved, i.e., there is no conversion of kinetic energy into other types of energy.

The concept of elastic collisions will enter into our discussion of a thermodynamic vari-

able known as internal energy, later in this chapter. In an inelastic collision, in contrast,

momentum is conserved (as it must always be) but kinetic energy is not. Of course, the total

energy of the system must be conserved, so that during an inelastic collision some kinetic

energy is converted to other types of energy (ultimately heat). Conversion of kinetic energy

to heat during inelastic collisions takes place, for example, when celestial bodies collide.

This process was responsible for accretionary heating during the Solar System’s formative

period (Chapter 2). On a very different scale, inelastic collisions of subatomic particles with

atoms in a crystal are the cause of radioactive heating, one of the key sources of energy in

terrestrial planets (Chapter 2).

Worked Example 1.2 Dissipation of kinetic energy during collisions of celestial bodies

(a) An asteroid of mass m

moves directly towards Earth (mass M ) with velocity ¯v

,as

measured from Earth. Consider a reference frame relative to which the Earth is initially at

rest (i.e. the Earth’s initial velocity is zero), but that will remain fixed even if the state of

motion of the Earth were to change. Figure 1.2a shows the initial situation as seen from this

reference frame, choosing a leftward-directed velocity as positive. We consider the collision

of the two bodies as being perfectly inelastic, meaning that momentum, ¯p, is conserved,

but kinetic energy is not. After the collision, the Earth and the asteroid merge into a single

body of mass (m

+M), moving with velocity ¯v

relative to the same reference frame

as before, which has not been affected by the collision. We seek the magnitude and the

direction (leftwards or rightwards) of ¯v

, the change in the velocity of the Earth relative

to the external reference frame, and the change in kinetic energy of the Earth + asteroid

system resulting from the collision.

12 Energy in planetary processes

M+m

–v

M+m

(a)

(b)

fixed reference frame

time

Fig. 1.2 Asteroid (mass m) colliding with Earth (mass M), as seen from Earth (a) and from the asteroid (b).

The final velocity is calculated from momentum conservation:

initial

= m ¯v

final

=(m +M)¯v

¯v

m +M

¯v

(1.14)

The change in the Earth’s velocity is simply v

, as its initial velocity in the chosen frame of

reference is zero. The amount of kinetic energy that is converted to other forms of energy

(chiefly heat) is given by:

k, final

−U

k, initial



(m +M)|¯v

−m|¯v



=−

m|¯v



m +M



. (1.15)

If the asteroid is small compared to Earth, then the expression in parentheses ≈ 1, and the

heat dissipated is essentially equal to the kinetic energy of the asteroid before the collision.

13 1.4 Expansion work

(b) We repeat the calculation from the point of view of a reference frame that is initially

at rest relative to the asteroid, and that, as before, is not affected by the collision (Fig. 1.2b).

In this case the Earth’s initial velocity is −¯v

and the asteroid’s initial velocity is zero.

Conservation of momentum is in this instance:

initial

= M

(

−¯v

)

final

=(m +M)¯v

∗

¯v

∗

m +M

(

−¯v

)

(1.16)

where the asterisk is used to remind ourselves that the final velocity in this case is measured

relative to a different reference frame, initially fixed to the asteroid. The change in the

Earth’s velocity is then given by:

 ¯v

Earth

=−

m +M

(

¯v

)

−

(

−¯v

)

m +M

¯v

, (1.17)

which is the same as the change calculated in part (a), compare equation (1.14). Note

carefully the meaning of the signs: equation (1.16) shows that after the collision the Earth

is still moving towards the right, but at a lower speed than before the collision. Equation

(1.17) shows that the velocity change is positive, i.e. leftwards. As seen from the asteroid’s

reference frame, the Earth has slowed down by the same amount as the Earth has speeded

up (from rest) when seen from the Earth’s reference frame. You should verify that the loss

of kinetic energy as calculated from the asteroid reference frame also agrees with the loss

calculated from the Earth’s reference frame, equation (1.15).

1.3.3 Energy dissipation

Energy dissipation is the conversion of any kind of non-thermal energy to heat. A process

that accomplishes this conversion is called a dissipative transformation. In the example of

an asteroid colliding with Earth kinetic energy is dissipated, i.e. it is converted to heat. The

full import of this definition will become clear in Chapter 4. For now, it is important to

realize that, although energy is conserved during a dissipative process (this is the First Law

of Thermodynamics), a full reversal of a dissipative transformation is impossible. In other

words, it may be possible to reconvert some of the heat back to mechanical energy, but

there is always a fraction of the heat generated by dissipation that can never be converted

back to non-thermal energy (this is the Second Law of Thermodynamics). Transformations

between different types of non-thermal energy are called non-dissipative, meaning that the

inverse transformation is, in principle, possible.

1.4 Expansion work. Introduction to equations of state

1.4.1 The concept of expansion work

Change in volume of any substance entails an energy transfer, in other words, a system that

undergoes a volume change either absorbs or releases energy. Energy transfer mediated by a

14 Energy in planetary processes

change in volume is called expansion work. If a substance expands, it is performing mechan-

ical work on its environment and, by the law of conservation of energy, this energy must

come from somewhere. Expansion of volcanic gas during a pyroclastic eruption is a process

in which a large amount of energy is transferred from a magmatic system to the atmosphere

by performing expansion work on the latter. Other examples are perhaps less eye-catching

but not less important: discontinuous phase transitions, such as vaporization and freezing

of water, are accompanied by expansion work, as are many mineral reactions. For instance,

consider the difference in density between the Al

SiO

polymorphs kyanite and sillimanite.

When kyanite transforms to sillimanite the volume of a fixed amount of Al

SiO

increases,

because its density decreases. This mineral transformation performs expansion work on its

environment. The converse is also true, when a system is compressed it absorbs mechanical

energy from its environment and this energy is stored in the substance. Transformation of

sillimanite to kyanite absorbs mechanical energy from the environment, and this energy is

stored as chemical energy in the crystal of kyanite (the expression “chemical energy” is for

the time being quite vague, it will take on a more precise meaning in subsequent sections

and chapters).

Dissipative compressions are an important source of heat in a wide range of planetary

processes. For example, air masses that descend rapidly in the atmosphere and protostellar

clouds of gas (such as the one that gave rise to our Solar System over 4.55 Ga) that contract

under their own gravitational pull, heat up as a result of compression, i.e. compression trans-

forms mechanical energy into thermal energy. In contrast, elastic materials, such as rocks

at relatively low temperatures, are able to undergo approximately non-dissipative changes

in volume, storing compression work (= negative expansion work) as elastic energy.

Expansion work, then, plays an important role in many planetary processes, but how do

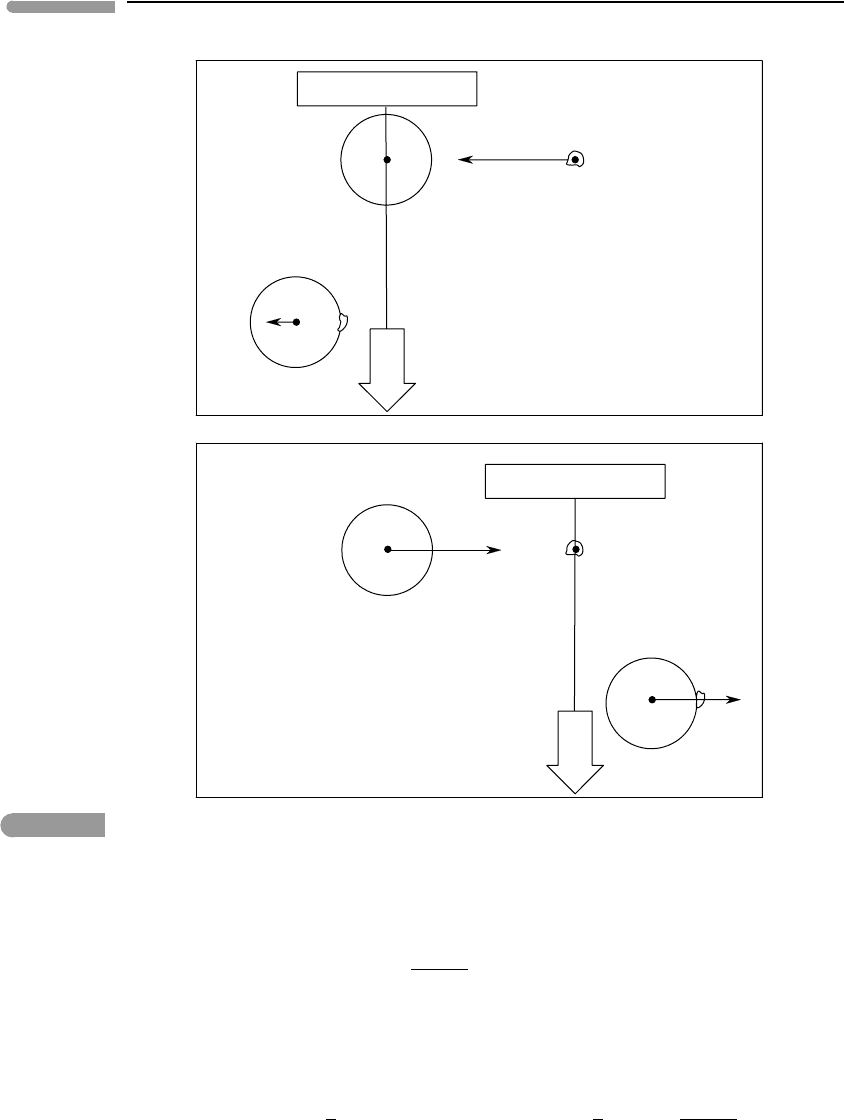
we measure it? Figure 1.3 shows a system of arbitrary shape expanding into an environment

that exerts a uniform pressure P. If the system’s surface area is A, then as the system expands

it must overcome a total force PA over its entire surface. Although PA is an oriented object

we are not using vector notation to represent it. This is careless notation, that we can justify

informally by noting that during uniform expansion pressure and force have the same

orientation as displacement, so that the inner product of the two objects equals the scalar

product of their magnitudes (Box 1.1).

Consider an infinitesimal expansion that causes the surface of the system to move out-

wards by an amount dx (Figure 1.3). Then the total amount of work performed by the system

during this infinitesimal transformation is:

dW = P Adx. (1.18)

The product Adx is the change in volume of the system, dV (because this is an infinitesimal

expansion, the total surface area can be considered to remain constant). The differential

expression for expansion work is then:

dW = PdV . (1.19)

The SI unit of pressure is the pascal (Pa), defined as a pressure of 1 N m

−2

, so that a volume

change of 1 m

against a pressure of 1 Pa performs 1 J of work. Another unit of pressure

that I find much preferable is the bar, where 1 bar = 10

Pa. One good reason to prefer the

bar over the pascal is that atmospheric pressure on Earth at sea level is approximately 1 bar,

so it is easy to develop an intuitive feeling for the magnitude of a pressure expressed in bar,

15 1.4 Expansion work

P+dP

P+dPP+dP

Fig. 1.3

Expansion work. The shell deﬁned by the two spheres is the increase in volume dv =Adx.

kbar or mbar. A convenient unit of volume is, then, J bar

−1

, where1Jbar

−1

= 10

−5

= 10 cm

. Expressing volume in J bar

−1

and pressure in bar, W comes out in J.

1.4.2 Quasi-static, reversible and irreversible processes

In the derivation of the expansion work formula I have been rather sloppy with the sign

convention, and this sloppiness must be corrected before we can advance any further. In

order to do so, we need to address another issue which is often the source of much confusion

and consternation when encountering thermodynamics for the first time. I stated that the

system expands “into an environment that exerts a uniform pressure P ” – but what is the

pressure inside the system? Classical thermodynamics is concerned only with states of

equilibrium. Because of this constraint, the only situation that can be rigorously addressed

with classical thermodynamics is one in which the pressure inside the system equals the

external pressure. But if the two pressures are the same, then why is the system expanding

at all? Here lies the problem, if the two pressures are the same then the system is static,

and there is no work being performed. Classical thermodynamics deals with this riddle by

inventing an idealized type of transformation called a quasi-static transformation. This is

a process that takes a system from an initial equilibrium state to a final equilibrium state by

means of an infinite number of intermediate equilibrium states that are infinitesimally close

to one another. Such a transformation is, of course, physically impossible. In our example of

an expanding system, we could visualize a situation in which the pressure inside the system

is always greater than the external pressure by an infinitesimal amount, dP. By this we mean

that the internal pressure is barely higher than the external pressure, so that the system does

16 Energy in planetary processes

expand, but not so much higher as to make any difference in the amount of expansion work

given by equation (1.19), i.e. we would get the same numerical result whether we used the

internal or the external pressure in our calculations.

A concept that is distinct to that of a quasi-static transformation, but is sometimes con-

fused with it, is that of a reversible transformation. By definition this is a process during

which there is no energy dissipation. A reversible transformation must be quasi-static, but

the converse is not true: a quasi-static transformation may dissipate energy, and thus be

irreversible. An example of this would be infinitesimally slow expansion of a gas (i.e. a

quasi-static process) accomplished by displacing a piston that slides inside a cylinder with

friction. The irreversibility arises from frictional heating. We will come across other exam-

ples that will gradually make the concepts of dissipation and irreversibility clear, and will

define these concepts rigorously using the Second Law of Thermodynamics (Chapters 4

and 12).

In contrast, the concept of a quasi-static transformation can be clarified by means of an

example. A gas is a collection of moving molecules. Consider what happens at the micro-

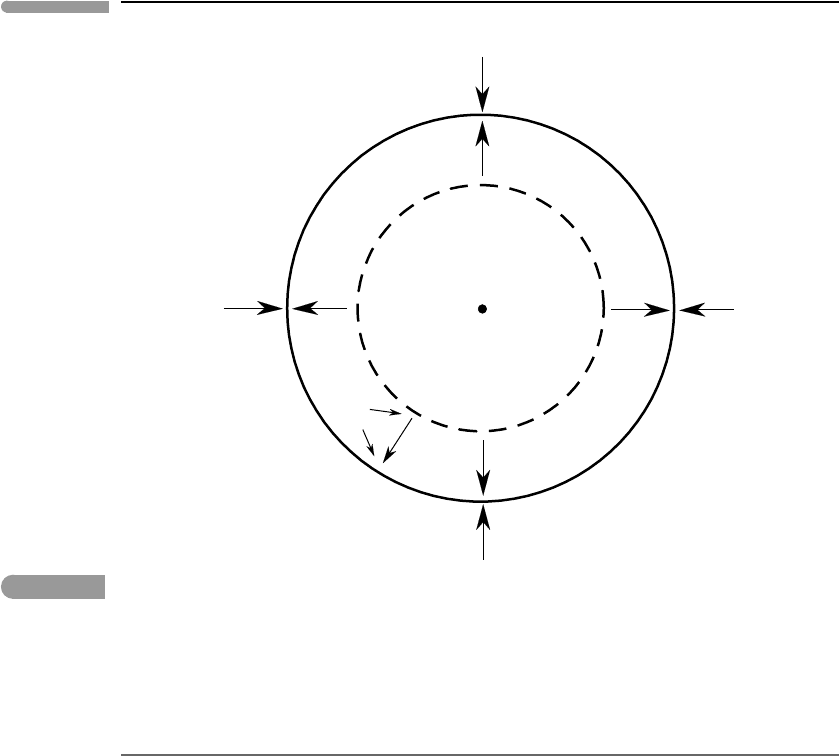
scopic level when a gas is subjected to an increase in pressure. The gas is at equilibrium if,

as a result of interactions among its molecules (i.e. collisions), the distribution of molecular

kinetic energies (or, equivalently, molecular speeds) is smooth, with a unique peak value

(Fig. 1.4) that specifies the most probable value of kinetic energy. The temperature of the

gas is a measure of this most probable kinetic energy value. Equilibrium in the gas is pos-

sible only if there has been sufficient time to allow its molecules to exchange information

throughout the entire volume occupied by the gas, so that all molecules “know” what the

most probable kinetic energy is. Information is transported by molecular collisions, so that

it travels at a rate comparable to molecular speeds. If the gas is now compressed at a rate

that is very slow relative to most molecular speeds then the gas will remain at equilib-

rium throughout the compression, because information about perturbations in one part of

the system reach the entire system before the magnitude of the perturbations can change

significantly. This is an example of a quasi-static transformation. In contrast, if the gas is

compressed at a rate that is much faster than the speed with which most molecules move,

then the gas cannot be at equilibrium. In this case a perturbation in one part of the system

can grow significantly before the rest of the system “knows” about it. Molecules in different

parts of the system will have different speed distributions, so that the speed distribution for

the entire volume of gas will not display a unique maximum value (dashed curve in Fig.

1.4). The fast compression is not quasi-static and, therefore, it is an irreversible transforma-

tion. During such an irreversible transformation it is not possible to define the temperature

nor the pressure of the gas, as there is no unique most probable molecular kinetic energy

(Fig. 1.4). Sonic booms, which occur when air is compressed at a rate that is faster than

characteristic molecular speeds, are examples of irreversible transformations of this type.

1.4.3 Measuring expansion work. Material properties and equations of state

We are now able to come to a rigorous definition of the sign of the expansion work. If the

pressure exerted by the system, P (we assume a quasi-static expansion), and the change in

volume, dV = Adx, have the same orientation, then PdV is a positive quantity. The work

performed by the system on the environment during expansion, dW , is a positive quantity.

This work represents energy transferred from the system to its environment, so that the

energy content of the environment changes by an amount dW , and the energy content of

the system that is expanding changes by an amount −dW . It is important to understand

17 1.4 Expansion work

0 500 1000 1500 2000 2500

0.001

0.002

Molecular speed (m s

–1

)

Probability density

Distribution of molecular speeds for N

200 K

500 K

1500 K

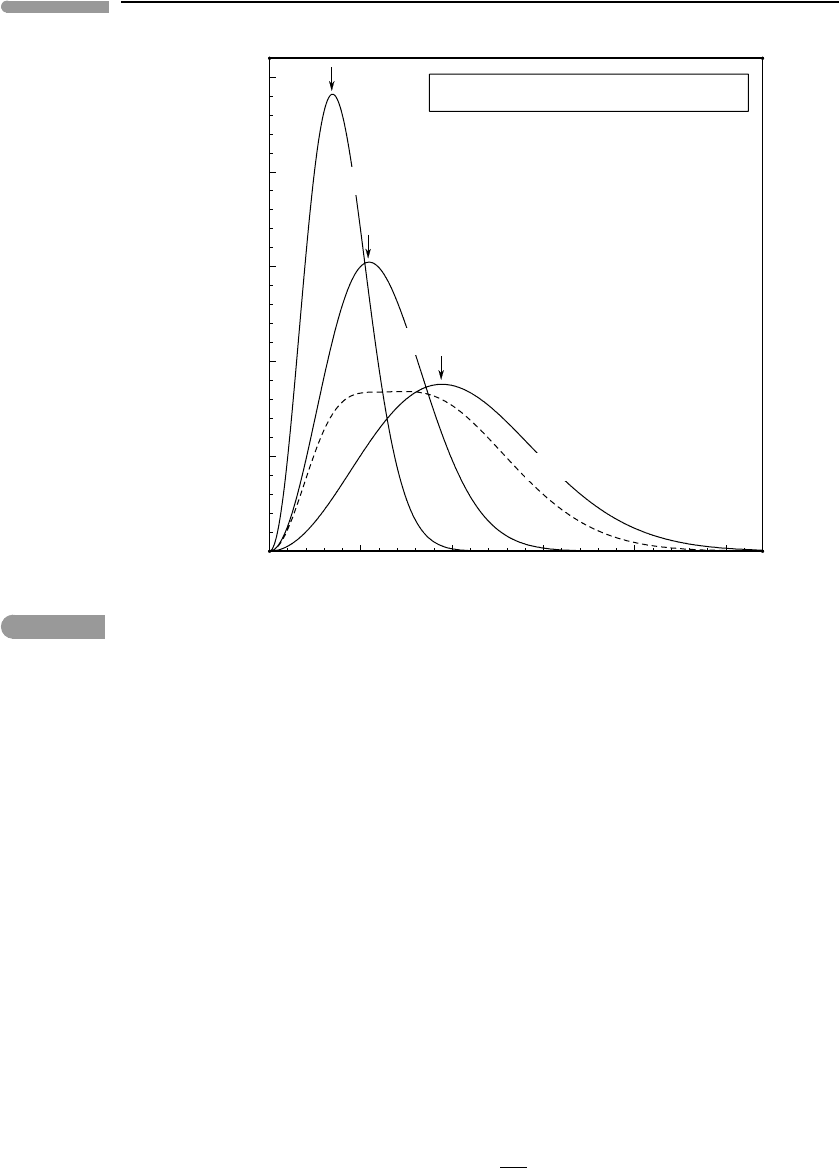
Fig. 1.4

Maxwell–Boltzmann probability density distribution for molecular speeds in N

(assumed to be an ideal gas) in the

absence of a gravitational ﬁeld. The areas under all the curves are unity. As temperature increases the probability

distribution becomes wider but there is always a unique most probable speed, that depends on temperature only

(arrows). The dashed line shows a hypothetical non-equilibrium distribution of molecular speeds – the most probable

speed, and hence the temperature, cannot be deﬁned in this case.

exactly what equation (1.19) is measuring and how to interpret the sign of the expansion

work that one calculates upon integrating this equation. Because P is always a positive

quantity, a positive value of W means that the system has expanded and performed work

on its environment; the system’s energy content has therefore decreased. Compression, i.e.

a decrease in the system’s volume, results in a negative value of W which implies that

the system has gained energy. This energy was extracted from its environment. This sign

convention is not universally followed, but it leads to equations that represent physical

processes in an intuitively satisfying way.

The expansion work associated with a finite change in volume is calculated by integrating

equation (1.19). Except for the special case of isobaric processes, volume and pressure are

not independent variables. In order to integrate equation (1.19), then, we need a function

that relates volume with pressure. One such function is the bulk modulus, K, which is a

material property, i.e. a parameter that has a well-defined value for every substance and is

independent of system size:

K =−V

∂P

∂V

. (1.20)