Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

608 Non-equilibrium thermodynamics

–14

–12

–10

[X] / [O

]

] / [O

]

–8

–6

–

0.2

0.4

0.6

0.8

=10

–8

=10

–10

=10

–12

=10

–14

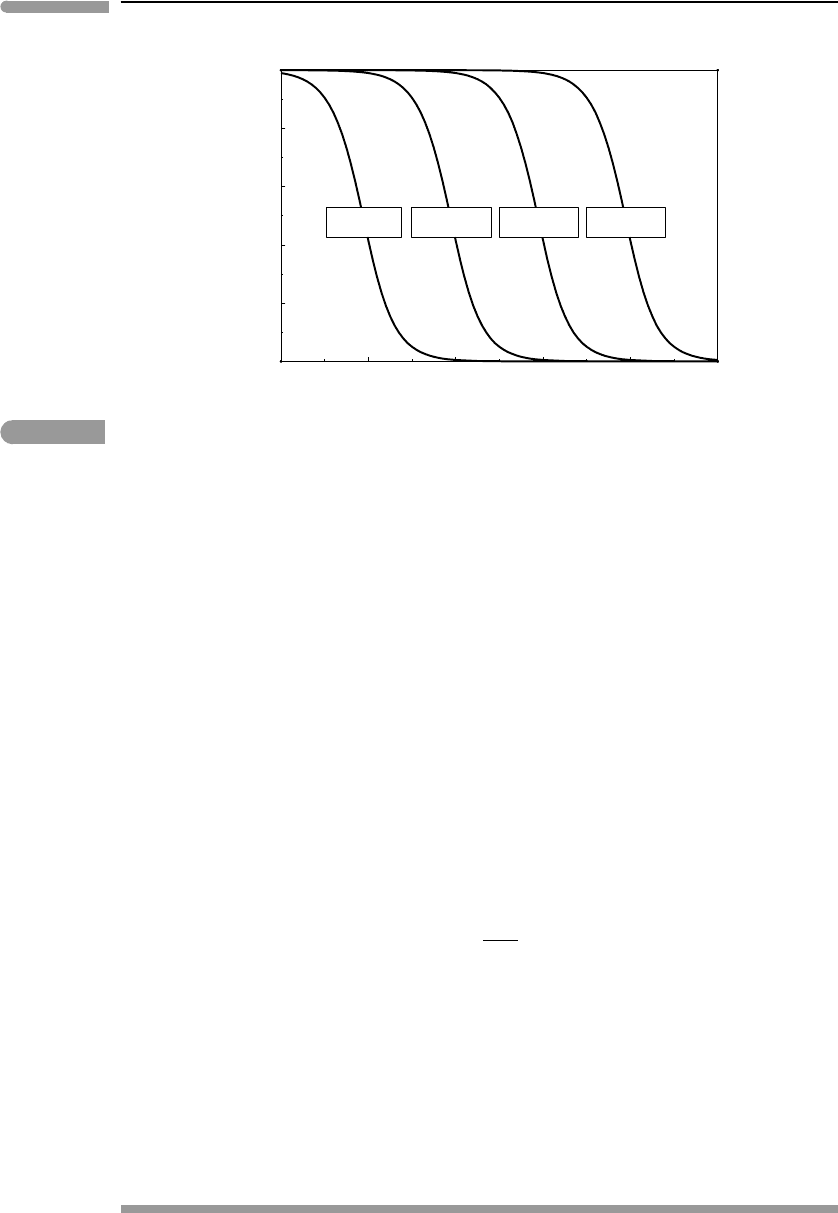
Fig. 12.5 Atmospheric ozone depletion caused by a catalytic cycle initiated by an active species X (X could be, for instance, OH,

NO or Cl). Numbers in boxes are values of the rate constant k

, for the reaction: X +O

→XO +O

,incm

molecule

−1

.[O

]

is the concentration of ozone in the absence of species X. Note that minuscule concentrations

of the active species X can wipe-out atmospheric ozone, and that there is a threshold value of [X] above which ozone

destruction increases rapidly.

cycles are in reality considerably more complex that the examples that we considered here

but the behavior depicted in Fig. 12.5 is qualitatively correct.

It is important to point out that the laws of thermodynamics are not “violated” by the

fact that ozone concentration in the atmosphere is not at equilibrium with that of oxygen.

This non-equilibrium ozone concentration is kept at a (more or less) constant level by a

continuous supply of energy, in the form of solar photons that split oxygen atoms in the first

reaction of the Chapman cycle (equation (12.114)). Production of ozone, and its persistence

in a concentration far greater than the equilibrium concentration, are dynamic processes that

depend on the continuous operation of this photochemical reaction. If ultraviolet radiation

were to be turned off permanently then ozone, and atomic oxygen, would convert to the

stable species O

, at rates dependent on the specific reaction mechanism.

The two first reactions of the Chapman cycle can be combined to yield reaction (12.113).

The enthalpy change for this reaction is 285.4 kJ. We can calculate the total energy of the

photons consumed by this reaction with the formula:

hcA

, (12.134)

where h is Planck’s constant, c is the speed of light, A is Avogadro’s number, and λ is the

wavelength of the photon. It is found experimentally that photodissociation of O

occurs for

photons of λ<240 nm (see also Chapter 13), from which we calculate U

> 498 kJ mol

−1

There is more than enough energy to account for the higher enthalpy of ozone relative to

oxygen. Where does the energy excess go? Because of conservation of momentum, the

photons’ momentum (= hν/c) must be transferred to the oxygen atoms, increasing their

translational kinetic energy. This energy influx is then distributed throughout the gas by

molecular collisions, increasing its temperature and therefore its entropy. We return to this

discussion in the next chapter.

609 12.4 Controls on rate constants

12.4 Controls on rate constants

Much of this chapter has focused on dynamic processes, by which we mean that the

thermodynamic state of the system changes with time. Rates are quantified by means of

“constants”, such as chemical diffusivities and reaction rate constants. But what determines

the values of these “constants”? We shall briefly discuss two important classes of processes:

thermally activated processes and photoactivated processes.

12.4.1 Thermally activated processes. Arrhenius law

The rates of many natural processes, such as chemical diffusion, viscous flow (which we

discussed in Chapter 3 and which, as we saw there, corresponds to diffusion of momen-

tum) and thermally activated chemical reactions, vary exponentially with temperature

according to:

Ψ =A exp



−



, (12.135)

where A and E

are positive constants and Ψ is a parameter that describes the charac-

teristic rate of the process. For example, Ψ can be the chemical diffusion coefficient D

(Section 12.2.2), the rate constant of a chemical reaction, k (Section 12.3.1), or the viscous

flow shear rate du/dx (Section 3.7.4). In the latter case the parameter Ψ is the rate of

shearing, which at constant shear stress is the inverse of the viscosity µ (equation (3.7)).

Because viscosity, rather than its inverse, is the parameter that is used to measure the rate of

momentum transfer the negative sign does not appear in the exponential factor of equation

(3.3.1). Otherwise that equation is identical to (12.135).

Equation (12.135) is known as Arrhenius law, after the Swedish physical chemist Svante

Arrhenius, who discovered it experimentally. If we think of Arrhenius law as an empirical

macroscopic relationship then it is not necessary to attach any physical meaning to the

constants A and E

. We can nonetheless note that E

has units of energy, and it is a

quantity known as the activation energy for the process in question. The units of A, known

as the pre-exponential factor, vary depending on what the parameter Ψ represents, but

they always include the factor [T ]

−1

. From a purely macroscopic point of view we can

think of A as the limiting value of Ψ at very high temperature. We can, however, attach

more specific physical meanings to the two constants, which relate to the microscopic

nature of the processes in question. In this view A is a quantity that is proportional to

the rate at which microscopic events take place. The exponential factor exp(−E

/RT )

is the probability that a given event will produce a specific outcome. For example, if Ψ

corresponds to the rate constant of a chemical reaction then the events would be molecular

collisions, and theexponential factor woulddescribe the probability that a given collision has

enough energy to break atomic bonds and result in chemical recombination. If Ψ describes

diffusion of matter or momentum then the events would be excursions of atoms away from

their equilibrium positions and the exponential factor would be the probability that a given

excursion is energetic enough to cause an atom to jump from its initial equilibrium position

to a neighboring one. In every case the probability tends to zero as temperature goes to zero.

Then no events have enough energy to accomplish the desired result, and the macroscopic

process stops. The probability tends to one at high temperature, so that all events accomplish

610 Non-equilibrium thermodynamics

the desired result and the rate of the macroscopic process approaches some maximum, but

finite, value.

Arrhenius law is a reasonably good first approximation to the behavior of thermally acti-

vated processes. Chemical diffusivities and reaction rate constants are commonly tabulated

in the form of values of the A and E

parameters in equation (12.135). An example is the

large database of reaction rate constants, from which the values used in Worked Exam-

ple 12.3 were obtained, maintained on-line by the U.S. National Institute of Science and

Technology (NIST Chemical Kinetics Database). A compilation of chemical diffusivity

parameters of geological interest (used in Worked Example 12.1) can be found in Zhang

(2008).

Equation (12.135) is not a complete physical picture, however. For example, it is found

that the pre-exponential factor is generally a function of temperature, and pressure depen-

dencies of the pre-exponential factor and the activation energy also exist. These macroscopic

effects point to a microscopic mechanism that is more complex than what I describe here.

Rigorous discussions of these topics can be found, for example, in the books by Logan

(1996); Houston (2006); Borg and Dienes (1988), and with specific focus on geological

processes, Poirier (1985) and Zhang (2008).

12.4.2 Photochemical processes

Thermal energy is incapable of initiating a chemical reaction if the resulting kinetic energy

of the molecules is not sufficient to break interatomic bonds. Even at low temperature, how-

ever, individual molecules may acquire excess energy and become reactive by absorbing

photons of specific wavelengths (see also Chapter 13). An example of this is the initiation

step of the Chapman cycle. At the temperature of the stratosphere, and even at temperatures

considerably higher than this, O

molecules do not have sufficient kinetic energy to disso-

ciate as a result of collisions, but a molecule of O

, regardless of its temperature, dissociates

when it absorbs an ultraviolet photon. This is not a thermal process, which means that it

does not rely on a statistical distribution of molecular speeds and on the probability that the

speeds of some molecules will exceed some characteristic threshold. The rate constants for

photochemical reactions are therefore not described by equation (12.135). Partly for this

reason it is customary to use a different symbol for the rate constants (j instead of k), even

if the rate laws are the same regardless of the nature of the activation process.

Photochemical reactions are activated by radiation within a specific range of wave-

lengths. For example, photodissociation of O

(the first reaction in the Chapman cycle)

requires ultraviolet photons with wavelengths shorter than 240 nm. There are reactions,

called radiolytic reactions, that require higher energy photons, in the X-ray and gamma

part of the spectrum. We can expect that the rate constant will vary directly with the inten-

sity of the radiation of the required wavelength (number of photons per unit of area per

unit of time, i.e., photon flux) and with the absorption cross section, which we can think

of as the effective target area offered by the molecules to the photon flux (more on this in

Chapter 13). We write this relation as follows:

j =



I (λ)σ (λ)dλ, (12.136)

where I (λ) is the photon flux at wavelength λ, σ (λ) is the absorption cross section, which

also varies with wavelength, and the integral is over the range of wavelengths within which

photoactivation takes place.

611 12.5 An introduction to kinetics

This equation is appropriate, for example, to photoactivation of a chemical reaction

in a laboratory environment. Photochemical reactions in planetary atmospheres are more

complicated, because the photon flux varies with elevation. It is maximum, and equal to the

incident solar flux, at the top of the atmosphere, and then decreases as photons are absorbed

by atmospheric gases. If, for the sake of simplicity, we consider only a hypothetical situation

in which solar radiation is always perpendicular to the planet’s surface (e.g. noon at the

equator on the day of the equinox), then we have, by Beer–Lambert’s law of radiation

(Section 13.2.4):

I (λ) =I

(λ)e

−τ

, (12.137)

where I

(λ) is the photon flux at the top of the atmosphere and τ

is a non-dimensional

absorption length, known as the optical thickness (Section 13.2.4), and given by (see also

equation (13.55)):



(λ)



(z)dz, (12.138)

where σ

is the absorption cross section of chemical species i, N

is the number density

of species i (molecules per unit volume), the integral is from the top of the atmosphere to

the elevation of interest, and the summation is over all atmospheric species that absorb at

wavelength λ. If the incident solar radiation is not perpendicular to the planet’s surface then

a geometric correction must be applied to Beer–Lambert’s law.

Substitution of (12.138)in(12.137), and then in (12.136), yields the value of the rate

constant as a function of elevation:

(z) =



(λ)e

−



(λ)



(z)dz

(λ)dλ, (12.139)

where σ

is the absorption cross section of the photoactivated molecule of interest. As we

should expect, this equation states that the rate constant decreases with increasing optical

thickness, i.e. as the planet’s surface is approached. Photochemistry is therefore a more

important process in the stratosphere than in the troposphere, for the simple reason that

there is a higher photon flux. The rate constants will obviously also vary with time of

day and season, as the angle of the incident solar radiation and hence the photon flux will

vary. Rate constants for atmospheric photochemistry vary over many orders of magnitude

across a planetary atmosphere. The values of j

and j

used in Worked Example 12.3

are approximate average values for the terrestrial stratosphere at an elevation of ∼30 km.

Since the rate of production and destruction of ozone is critically dependent on these rate

constants, it follows that the numerical results obtained there change with elevation.

12.5 An introduction to kinetics of heterogeneous processes

The kinetic behavior of homogeneous processes, such as chemical reaction in a homoge-

neous phase or diffusion in a single continuous phase, can be set-up mathematically in

a relatively straightforward and unambiguous fashion – which of course does not mean

that the resulting equations are necessarily easy to solve. The mathematical description

of the kinetics of heterogeneous processes is less straightforward. It commonly involves

612 Non-equilibrium thermodynamics

sets of coupled differential equations that describe rates of chemical reaction, heat transfer

and mass transfer. Simplifying assumptions are sometimes possible, though. Consider the

following three simple examples.

(i) Crystallization of enstatite from a basaltic melt, which we can schematize as follows:

MgO

melt

+SiO

2 melt

 MgSiO

3 crystal

(ii) Devolatilization of the assemblage magnesite + quartz:

MgCO

3 crystal

+SiO

2 crystal

 MgSiO

3 crystal

+CO

2 vapor

(iii) Weathering of enstatite at the Earth’s suface:

MgSiO

3 crystal

+3H

O  Mg

SiO

4aq

+2OH

−

One way of analyzing the kinetic behavior of heterogeneous reactions such as these is to

assume that the locus of the chemical reaction is a homogeneous region of infinitesimal

extent, which we may call the reaction volume or reaction interface (Zhang, 2008). The

rate of the chemical reaction is then a function of its rate constant and of the affinity of the

reaction inside the infinitesimal reaction volume (equation (12.74)). The rate constants of all

three of these reactions are functions of temperature (equation (12.135)), and the affinity,

which is a linear combination of chemical potentials, varies with temperature, pressure

and composition. As the reactions proceed enthalpy is liberated or absorbed, and chemical

species are consumed and produced. The temperature and affinity in the reaction volume are

therefore determined by the relative rates of chemical reaction and heat and mass exchanges

between the reaction volume and its environment.

Crystallization of enstatite from a melt (reaction i) liberates enthalpy (

H<0) and

consumes MgO and SiO

melt components. If the reaction volume were a closed system

then its temperature would increase and the concentrations of the reactants would decrease.

From the definition of affinity, equation (12.70), we can see that:

∂E

∂T

=

S =



(12.140)

and:

∂E

∂X

> 0, i : reactant. (12.141)

In a closed reaction volume the affinity would decrease and hence the reaction would slow

down, and eventually stop. There would also be an effect on the rate constant that would act

in the opposite direction, but this is likely to be minor at magmatic temperatures, at which

chemical reaction rates are always fast. In reality, however, crystallization sets up gradients

in temperature and chemical potential between the reaction volume and the surrounding

melt, so that heat is carried away from the reaction volume and chemical components are

transported towards it. If we assume that diffusion is the transport mechanism for both

heat and chemical components then we can conclude that mass transfer is the rate-limiting

process, as heat diffusivity at magmatic temperatures is ∼6 orders of magnitude greater

than chemical diffusivity (see Worked Examples 12.1 and 12.2). As a first approximation,

then, the kinetics of reaction (i) could be treated as a chemical diffusion problem.

613 12.5 An introduction to kinetics

Consider now reaction (ii). This reaction is endothermic (

H>0) so that, if it took

place in a closed system, the temperature would decrease and the fugacity of CO

would

increase. If the gas phase is a product then differentiation of (12.70) yields:

∂E

∂f

< 0, j : product (12.142)

so that it follows from (12.140) and (12.142) that the affinity in a closed reaction volume

would go down. Let us assume for the sake of argument that the decarbonation reaction (ii)

occurs in a permeable setting, in which,for example, a network of cracks allows the gas phase

to escape as soon as it forms. If, as in the previous case, the temperature is high enough that

the reaction rate is much faster than heat diffusion, then we can consider two end-member

situations. If grain size is “infinitesimally fine” and the mixture of minute magnesite and

quartz crystals is perfectly random then we might be able to ignore mass transfer rates and

assume that the rate-limiting process is heat diffusion. For any “geologically reasonable”

grain size, however, it is likely that mass transfer will determine the rate of reaction (ii), but

there is an important qualitative difference with the crystallization reaction (i). In that case

diffusion of Mg and Si cations in the melt phase does not present a conceptual problem, but

in the case of the solid-state reaction (ii) this is not so. How do SiO

and CaCO

components

migrate to the reaction volume where enstatite and CO

are produced? Does this happen

by solid-state diffusion? If so, which are the chemical species that actually diffuse, and

what is the underlying atomic lattice through which they diffuse? Or does mass transfer

take place by dissolution of the reactants in a fluid phase, for example the CO

produced

by the reaction itself, and migration of the fluid phase? The rate-determining process may

be difficult to pin down, and even more difficult to quantify.

In the case of the weathering reaction (iii) we may assume that circulation of meteoric

water, i.e. advection, is the mechanism that accounts for both heat and mass transfer. Given

that advection is much faster than diffusion, and that fromArrhenius law (equation (12.135))

we can expect a small value of the rate constant for the chemical reaction at room temper-

ature, we may infer that weathering rates are likely to be controlled by chemical reaction

rates. The chief difficulty in quantifying the process in this case would be in the experimental

determination of the required rate constants.

Worked Example 12.4 Relationships between affinity and progress variable

The attentive reader should have noticed that the statement that I made regarding reactions

(i) and (ii), to the effect that in a closed system the affinity of a reaction decreases as the

reaction proceeds, is always true. In fact, it is an alternative way of stating the Second Law

of Thermodynamics, which we can summarize as follows:

∂E

∂ξ

≤0. (12.143)

The inequality holds true in a closed system – it simply states the fact that in a spontaneous

chemical reaction the Gibbs free energy of the products is lower than that of the reactants.

In order for the equality to be true the rates of heat and mass transfer between the reaction

volume and its environment must exactly match the rates of change of enthalpy and chemical

species concentrations caused by the reaction.Assume for simplicity that a chemical reaction

614 Non-equilibrium thermodynamics

occurs in the linear regime defined by equation (12.80) (i.e. close to equilibrium, see also

Exercise 12.2). We can re-write this equation as follows:

∂ξ

∂t

E , (12.144)

where k

is a positive constant. To begin with, we note that (12.144) says that a chemical

reaction can only take place beginning from a non-equilibrium condition, as the reaction

rate vanishes for E =0. This means that some degree of overstepping is always required in

order for reactions to occur in nature. For example, melting can only begin at a temperature

higher than the solidus, and crystallization cannot begin until temperature drops below the

liquidus. According to equation (12.144), the amount by which the reaction is overstepped

(i.e. the value of E ) will determine the rate at which melting or crystallization proceeds. We

can now look at different ways in which E may vary with the progress variable ξ .

Assume first that E is a constant. This could happen, for instance, during crystallization

of a well-stirred one-component system (e.g. ice from pure H

O), or during crystallization

from a very large reservoir of low-viscosity liquid (e.g. ocean water). Defining the value of

the progress variable at t =0asξ

=0 we have:

ξ =k

E t, (12.145)

which states that the reaction will proceed indefinitely. The behavior becomes more inter-

esting if we consider the inequality in (12.143). This means that either heat or mass transfer

are not able to keep up with the chemical reaction rate. The exact functional form of the

derivative ∂E /∂ξ may be difficult to determine, but we can choose the simplest possible

function as an example. This is the linear law:

∂E

∂ξ

=−k

, (12.146)

where k

is another positive constant. This constant must contain information about the

efficiency of the rate controlling process. For instance, if the rate is controlled by chemical

diffusion then k

must vary inversely with diffusivity: the lower the diffusivity, the more

the affinity will decrease with reaction progress, and thus the larger the magnitude of k

must be. Let the affinity at ξ

=0beE

. Then:

E = E

−k

ξ (12.147)

so that, substituting in (12.144) and integrating:

ξ =



1 −e

−k



. (12.148)

We now note that the reaction goes to completion as t →∞and that, because k

and k

are

positive constants:

lim

t→∞

ξ =

. (12.149)

Say that the process that we are modeling is crystallization from a silicate melt and that

we assume, rather simplistically, that the magnitude of the progress variable ξ represents

615 Exercises for Chapter 12

crystal size. Chemical diffusivity in melts varies inversely with viscosity, so that k

varies

directly with viscosity. Equation (12.149) then states that crystals that grow from a viscous

melt (e.g. a water-poor rhyolite) should be smaller than those that grow from a fluid melt

(e.g., a water-saturated pegmatite).Although during magmatic crystallization there are addi-

tional complications that we have ignored, most notably the generation and availability of

nucleation sites, equation (12.149) provides at least a qualitative kinetic explanation for an

observation that we became familiar with during our introductory physical geology course.

Exercises for Chapter 12

12.1 Derive the full set of interdiffusion equations, including the Onsager reciprocal terms,

for a ternary system consisting of two dilute solutes and a solvent (Section 12.2.3).

12.2 Find a linear approximation to (12.74) by writing r

= r

f ,eq

+δr

, where r

f ,eq

the rate of the forward reaction at equilibrium, by lineariting the exponential function

for

<< 1. Use your linearized expression to find a relationship between the phe-

nomenological coefficient L and r

. Establish a criterion by which a reaction can be

considered to be close to equilibrium.

12.3 Write differential and integral rate laws for the elementary reactions:

(i) 2A →products

(ii) 3A →products

(iii) 2A +B →products

(iv) A +B +C → products.

(Hint: use Maple wherever possible.)

12.4 Find expressions for the half lifes and time scales of the elementary reactions:

(i) 2A →products

(ii) A +B →products

(iii) 2A +B →products.

For (ii) and (iii) consider three cases: [A

]=[B

], [A

]>> [B

] and [A

]<< [B

12.5 Compare the exact solution for the concentration of a short-lived species [B]

(equation (12.104)) with the steady state solution (12.105). Establish a criterion for

how much time must be allowed to elapse for the steady state solution to become

an acceptable approximation. Also, describe some conditions under which the steady

state solution is never an acceptable approximation.

12.6 Estimate what would be the half life of ozone in the terrestrial atmosphere if ultraviolet

radiation were to stop suddenly. Comment on likely night vs. day variations in ozone

concentration.

Topics in atmospheric thermodynamics and

radiative energy transfer

This chapter seeks to answer three basic questions about the physical nature of planetary

atmospheres. First, why do some planets have atmospheres and others do not? Second, what

controls the mass and the thickness of a planetary atmosphere? Third, how is a planet’s

surface temperature affected by the existence of an atmosphere? Some of the answers that

we find here will be the starting point for our discussion, in the last chapter, of the chemical

evolution of atmospheres in the terrestrial planets and the possible relationships between

atmospheric composition and the origin of life.

13.1 Gravitational binding of planetary atmospheres

Whether or not a planet has an atmosphere depends on the relationship between the gravita-

tional potential at the planet’s surface and the translational kinetic energy of gas molecules.

The latter is of order k

T (Section 1.14), whereas the gravitational potential at the planet’s

surface can be written as Φ =4/3πGr

ρ (from equation (1.8)). Recalling that Φ is gravita-

tional potential energy per unit mass, we take the product Φu, where u =1.66054×10

−27

is the atomic mass unit, and form the non-dimensional ratio:

^ =

4πGr

ρu

. (13.1)

The parameter ^ is an estimate of the tendency of a planetary atmosphere to escape. For

reasons that we will see later the absolute value of ^ does not have a rigorous interpretation,

but the relative value among different planets is a good indicator of whether or not a planet

is likely to have an atmosphere, and, to some extent, of what type of volatile species may

be most abundant. The smaller the value of ^, the more strongly bound an atmosphere is,

and the more likely it is to contain a large proportion of low molecular weight species.

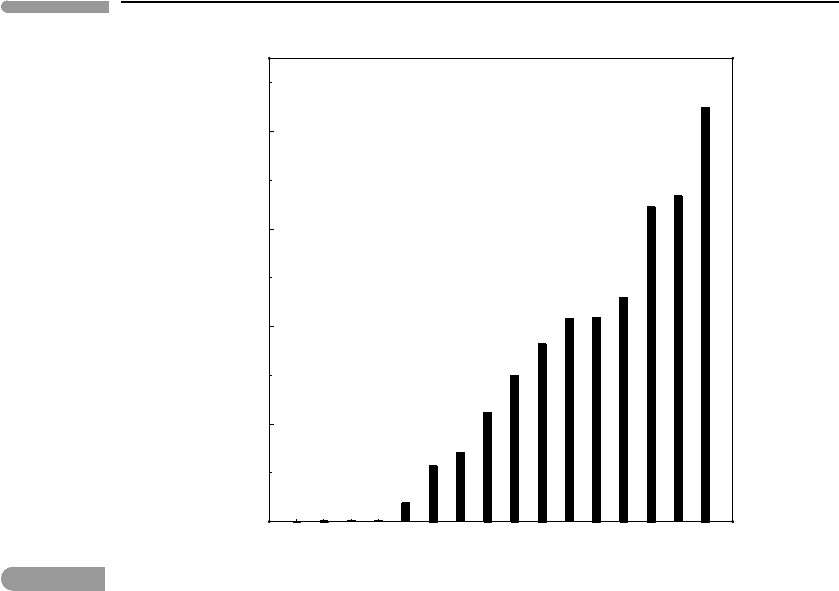
Calculated values of ^ for planets and major moons are shown in Fig. 13.1, arranged

in order of increasing value of ^. The value of T used in this graph is the temperature at

the planet’s surface (or its equilibrium temperature, Worked Example 13.1). As we shall

see this is not the best choice, but it is the simplest one. Regardless, we note that, with

one exception, the parameter ^ discriminates correctly between bodies with “substantial”

atmospheres (to the left of Triton) and those without one (to the right of Triton). Triton’s

faint atmosphere marks the boundary. The exception is Pluto, which is thought to have an

atmosphere comparable to that of Triton, but given the non-trivial uncertainties in Pluto’s

physical parameters the significance of this is not clear – it will likely remain unresolved

until the New Horizons spacecraft arrives in the Pluto–Charon system in 2015. Ignoring this

exception, equation (13.1) shows, for instance, that the reason why Titan has an atmosphere

but none of the Galilean satellites of Jupiter does is the fact that they lie closer to the

616

617 13.1 Gravitational binding of planetary atmospheres

0.2

0.4

0.6

0.8

Planetary body

Jupiter

Saturn

Neptune

Uranus

Earth

Venus

Mars

Titan

Triton

Ganymede

Pluto

Callisto

Mercury

Europa

Moon

Fig. 13.1

Value of the non-dimensional parameter ^ (equation (13.1)) for the planets and large moons of the Solar System.

Triton marks the boundary between bodies with atmospheres (to the left) and airless bodies (to the right), the one

outlier being Pluto.

Sun. Interestingly, the plot suggests that Europa is as unlikely to be able to hold on to an

atmosphere as Mercury, and that the Moon is even more hopeless in this respect.

Focusing on the left side of the plot, we note that the four giant planets have very small

^ values, ranging from 0.0007 to 0.003. This means that their atmospheres are bound very

tightly, but it also means something else. In equation (13.1) I used a constant mass, u,to

obtain the non-dimensional parameter ^, but the masses of different gas species, and hence

their gravitational binding energies, differ. For instance, the gravitational potential energy

of an H

molecule (mass =2) is more than twenty times smaller than that of a CO

molecule

(mass =44).At a given temperature, however, their kinetic energies are the same, so that the

hydrogen molecule is much more likely to escape than the carbon dioxide molecule. We can

also think of this in terms of velocities: the gravitational potential determines the planet’s

escape velocity (Section 2.4.1), whereas molecular speeds are a function of temperature

and molecular mass (Section 1.14). Molecular speeds follow a statistical distribution with

long “high speed” tails (Fig. 1.12), so that it is generally the case that only some fraction

of the total number of gas molecules in a planetary atmosphere have speeds greater than

the planet’s escape velocity. The rate at which gases can escape a body’s gravitational

attraction varies directly with the fraction of molecules that have speeds that exceed the

escape velocity, and at a given temperature this fraction is greater for light species (e.g. H

)

than for heavy ones (e.g. CO

). We can then (qualitatively) interpret a very small value of

the parameter ^ as signifying that even light molecules will generally be able to remain

gravitationally bound to the planet, because only a very small portion of the high velocity