Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

638 Topics in atmospheric thermodynamics

define two “average” values for each parameter, one for the ultraviolet and visible wave-

lengths that make up most of solar radiation, and the other one for infrared wavelengths

radiated by the planet’s surface and atmosphere.

The active atmospheric layer is at a constant and uniform temperature T

. It reflects a

fraction R

a,λs

of the incoming short wavelength solar radiation, with characteristic wave-

length λs, and absorbs a fraction A

a,λs

of this radiation. This absorption could take place,

for example, as a result of ozone-forming and ozone-destroying reactions. The transmit-

ted fraction of the solar energy flux, Θ

a,λs

= 1 − (A

a,λs

+ R

a,λs

), reaches the planet’s

surface, which is opaque to all electromagnetic radiation. We will assume that the atmo-

sphere does not reflect sunlight downwards, i.e., for sunlight reflected from the planet’s

surface, we will set R

a,λs

= 0 and Θ

a,λs

= 1 − A

a,λs

. The reason for this is to avoid

dealing with second and higher order internal reflections, which obscure the calculations

without providing any important insight, nor affecting the results in any significant way.

The average absorptivity of the surface for solar radiation is A

g,λs

and its reflectivity is

g,λs

= 1 −A

g,λs

. Solar radiation is thermalized and re-emitted at the average temperature

of the planet’s surface, T

. The emissivity of the ground for long-wavelength thermalized

radiation, characterized by wavelength λt,is/

g,λt

. Abusing somewhat equation (13.42),

we will assume that the absorptivity of the ground for thermalized radiation is equal to

the emissivity, i.e. A

g,λt

= /

g,λt

and since the ground is opaque at all wavelengths, R

g,λt

= 1 − A

g,λt

. The absorptivity and emissivity of the atmospheric layer for thermalized

radiation are also considered to be equal to each other, i.e. A

a,λt

= /

a,λt

, and we assume

that the atmosphere does not reflect long wavelength radiation either, i.e. A

a,λt

+ Θ

a,λt

= 1. We assume that convection does not take place in the atmosphere, so heat transport

is by radiation only, and that there are no other complications such as phase transitions

(e.g. cloud formation) and latitudinal variations in solar irradiation. Our goal is to find the

equilibrium temperatures of the ground and of the active atmospheric layer, T

and T

respectively.

We will solve for the energy fluxes emitted by the ground and by the active atmospheric

layer, F

and F

, which are related to the respective temperatures by the Stefan–Boltzmann

law:

a,λt

σ T

(13.56)

and:

g,λt

σ T

. (13.57)

We need two equations in the two unknowns, F

and F

. Our first equation is the bulk

planetary energy balance. This is an expanded version of the problem that we solved in

Worked Example 13.1. In order for the planet to be in thermal equilibrium it must radiate

energy to space at the same average rate as it receives it from the Sun, but now there is

radiation from both the surface and the atmosphere, and some of the short wavelength

sunlight is reflected without being thermalized. Recall from Worked Example 13.1 that

incident and reflected solar energy fluxes act over the cross section of the planet that

intersects the solar photon flux, πr

, whereas thermalized fluxes are radiated over the

entire surface area of the planet and atmosphere, 4πr

. The energy flows that we need to

639 13.3 Radiative energy transfer

consider, shown in Fig. 13.7, are as follows.

Solar radiation reflected to space by atmosphere: πr

a,λs

Solar radiation reflected by planet surface: πr

a,λs

)

g,λs

(recall that we assume that the atmosphere does not reflect sunlight downwards).

Thermalized radiation from planet’s surface: 4πr

a,λt

Thermalized radiation from top of atmosphere: 4πr

Thermalized radiation from atmosphere reflected from planet’s surface:

4πr

g,λt

a,λt

The sum of all of these terms is the energy radiated by the planet, so that at thermal

equilibrium this sum must equal the total energy received from the sun, πr

. With

some algebra we find that the planetary energy balance simplifies to:

=4k

+4Θ

a,λt

, (13.58)

where the two parameters k

and k

combine terms as follows:

=1 −R

a,λs

−Θ

a,λs

g,λs

=1 +Θ

a,λt

g,λt

. (13.59)

The parameter k

is the fraction of solar energy that is effectively absorbed by the planet, and

is the total thermal energy radiated by the atmosphere that escapes to space, including the

direct upwards flux and the fraction of the downwards flux that is reflected by the planet’s

surface.

For our second equation we can choose to balance energy either at the planet’s surface or

in the atmosphere. We can choose either one, but regardless of which one we choose we must

get the same results. I will choose energy balance at the surface, as the equations are simpler.

As an exercise, you should redo the calculations using energy balance in the atmosphere

(Exercise 13.13). In order for the temperature of the planet’s surface to be constant with

time the flow of thermalized energy emitted by the planet’s surface, 4πr

, must equal

the total radiant energy absorbed by the surface, which comprises the following two terms

(see Fig. 13.7).

Thermalized radiation from bottom of atmosphere: 4πr

g,λt

Absorbed solar radiation: πr

a,λs

g,λs

Equating and simplifying, we find:

a,λs

g,λs



−A

g,λt



. (13.60)

The solutions that we seek for the fluxes of thermal energy emitted by the surface and the

atmosphere are:

g,λt

a,λs

g,λs

+Θ

a,λt

g,λt

(13.61)

−Θ

a,λt

a,λs

g,λs

+Θ

a,λt

g,λt

, (13.62)

640 Topics in atmospheric thermodynamics

which we convert to ground and atmospheric temperatures with equations (13.56) and

(13.57).

We now use these equations to analyze the effects of some of the radiative energy transfer

parameters on average global temperature. Among these, the following are the ones that are

likely to be most variable.

(i) A

a,λt

, the long-wavelength absorptivity of the atmosphere, which is sensitive to the

atmospheric concentration of infrared active molecules such as CO

O and CH

(ii) R

g,λs

, the reflectivity of ground for solar radiation (i.e. the albedo of the planet’s

surface), which is strongly affected by ice and snow cover, as well as by vegetation.

(iii) R

a,λs

, the fraction of solar radiation reflected by the upper atmosphere, which can

be affected by fine dust, soot and sulfur dioxide crystals such as can be produced by

volcanic eruptions, meteorite impacts and missile-launch-button-happy individuals.

We study the effects of these three parameters, and assume that the absorptivity of the

atmosphere for solar radiation, which is controlled to a significant extent by oxygen con-

centration, and the absorptivity of the ground for infrared radiation have the constant values

a,λs

= 0.2 and A

g,λt

= 0.95 (hence, R

g,λt

= 0.05). We will also assume that the solar

constant equals its present-day value of 1368 Wm

−2

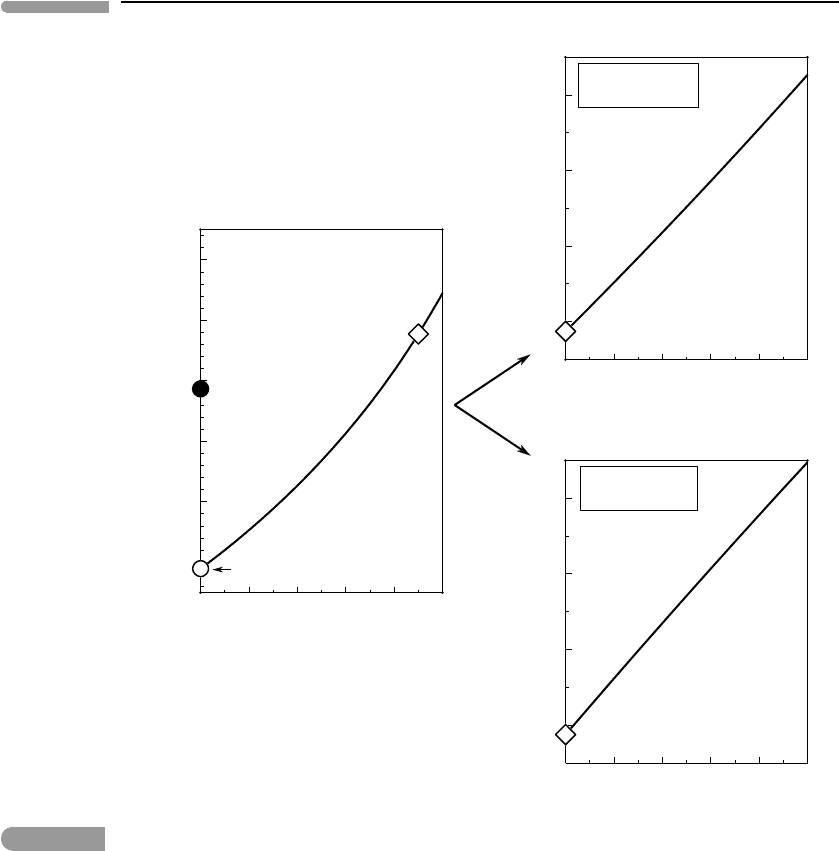
Figure 13.8 shows the effects of A

a,λt

and R

g,λs

. The solid circle on the leftmost panel

shows the equilibrium temperature for a black body Earth (∼ 278 K, see Worked Example

12.3). We then add A

a,λs

=0.2 and A

g,λt

=0.95 and reasonable values (taken from de Pater &

Lissauer, 2001, and Chamberlain & Hunten, 1987) for the present day surface albedo (R

g,λs

= 0.3) and atmospheric reflectivity (R

a,λs

=0.1). Without greenhouse warming (A

a,λt

=0)

the equilibrium ground temperature drops to ∼249 K, shown by the open circle. The diagram

shows that a temperature comparable to the present-day average surface temperature of the

Earth (∼288 K, shown by the diamond) is attained with A

a,λt

=0.9. This is our starting point

for the other panels in the figure. The one on top shows the effect of increasing A

a,λt

beyond

this value while holding the albedo, R

g,λs

, constant. An increase of ∼10% in the infrared

absorptivity of the atmosphere raises ground temperature by about 8 K. To put this number in

perspective, the increase in global temperatures since the Pleistocene is about 6 K, of which

1–2 K are the result of anthropogenic causes since the Industrial Revolution. Rising global

temperatures cause glaciers and sea ice to melt, lowering the planetary albedo. The effect

of decreasing R

g,λs

at constant A

a,λt

= 0.9 is shown in the bottom center panel. In reality

both parameters are coupled: as A

a,λt

increases so does global temperature, causing R

g,λs

drop. The functional relationship between the two parameters is complex and is in fact one

of several sources of uncertainty in global warming models. The coupling does not depend

on radiative heat transport, but rather on physical, chemical and biological interactions

between the atmosphere, the oceans and the solid surface. The figure suggests that a strong

coupling between the two parameters can plausibly raise average global temperatures by

10–15 K, which may result in ice-free conditions comparable to those that existed during

much of the Mesozoic.

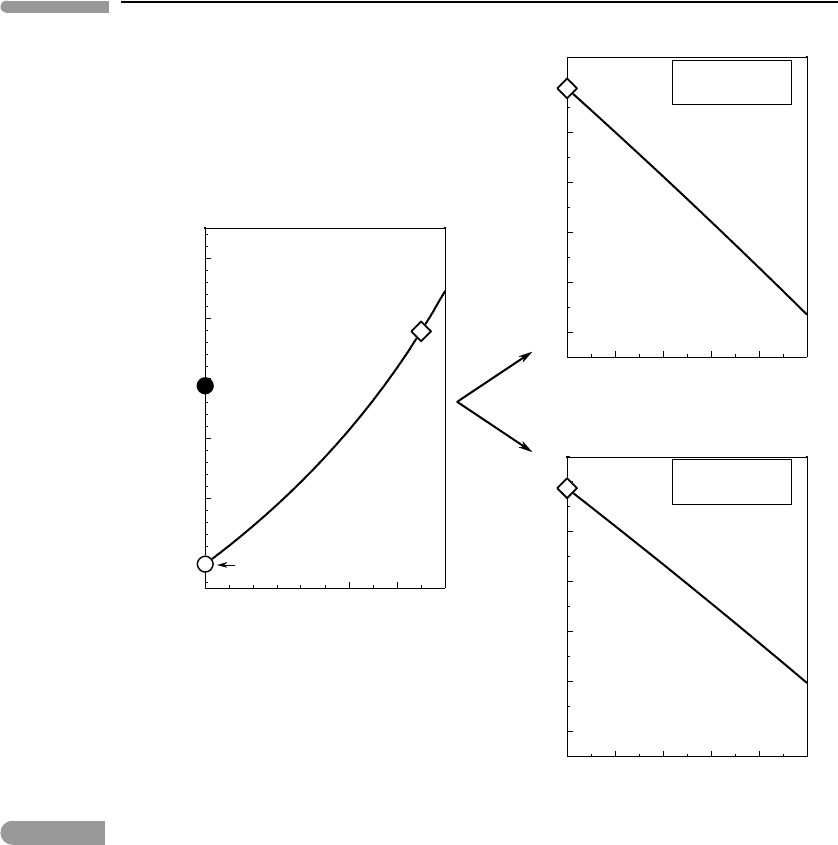
The effect of changes in the solar radiation reflectivity of the atmosphere, R

a,λs

, is shown

in Fig. 13.9. Here we keep A

a,λt

constant at 0.9. In the top panel we vary R

a,λs

from 0.1

to 0.2, while keeping R

g,λs

constant. As global temperatures drop, one expects that ice

and snow cover will increase, raising the planetary albedo and thus further lowering surface

temperatures (bottom right panel).As in the previous case, coupling between the two effects

is very complex and I will not attempt to include it. Strong coupling in this case could lead

641 13.3 Radiative energy transfer

0 0.2 0.4 0.6 0.8 1

250

260

270

280

290

300

Surface T (K)

0.9 0.92 0.94 0.96 0.98 1

288

290

292

294

Surface T (K)Surface T (K)

0.220.240.260.280.3

288

290

292

294

Black body T

g,λ s

= 0.3

g,λ s

= 0.3

a,λ t

= 0.9

a,λ s

= 0.1

a,λ t

Earth today

Fig. 13.8

Left: the Earth’s equilibrium black body temperature (278 K) decreases to 249 K when the non-zero reﬂectivities of the

atmosphere (R

a,λs

) and planetary surface (R

g,λs

) are taken into account. Present-day average temperature (diamond)

requires long-wavelength absorption coefﬁcient in the atmosphere A

a,λt

=0.9. Right top: effect of increasing

atmospheric long-wavelength absorption A

a,λt

while leaving other parameters constant. Right bottom: effect of

decreasing surface short-wavelength reﬂectivity R

g,λs

(i.e. decreasing the albedo of the planet’s surface) while

leaving other parameters constant. One should expect positive feedback between A

a,λt

and R

g,λs

: the increase in

temperature caused by greater long-wavelength atmospheric absorption melts ice, which lowers short-wavelength

reﬂectivity of the planet’s surface. This effect is not included in the ﬁgure.

to average global temperatures that are near freezing, perhaps as happened on Earth during

widespread late Proterozoic glacial periods.

Atmospheres are much more complicated systems than this simple toy model. Nonethe-

less, because radiative heat transfer is the only way in which a planet exchanges energy with

its space environment, the model does capture some important qualitative aspects. First,

without greenhouse warming the Earth might not be a habitable planet. Second, planetary

642 Topics in atmospheric thermodynamics

250

260

270

280

290

300

Surface T (K)

Surface T (K)Surface T (K)

0.1

0.30 0.32 0.34 0.36 0.38 0.

0.12 0.14 0.16 0.18 0.

278

280

282

284

286

288

278

280

282

284

286

288

Black body T

Earth today

0 0.2 0.4 0.6 0.8 1

g, λ s

= 0.3

g,λ s

= 0.3

a, λ s

= 0.1

g, λ s

a, λ s

= 0.1

a, λ t

a, λ s

Fig.13.9

LeftpanelisthesameasinFig.13.8.Righttop:effectofincreasingatmosphericshort-wavelengthreﬂectivityR

a,λs

while leaving other parameters constant. Right bottom: effect of increasing surface short-wavelength reﬂectivity

g,λs

while leaving other parameters constant. There is coupling between both parameters, as the temperature drop

caused by increased reﬂection of sunlight by the atmosphere increases ice cover and therefore surface albedo. This

effect is not included in the ﬁgure.

surface temperatures are determined by several radiative heat transfer parameters, of which

atmospheric absorptivity in the infrared is one. Other parameters that have comparably

strong effects are the short-wavelength reflectivity of the planet’s surface and of the atmo-

sphere. Relatively small changes in the values of any of these parameters can cause shifts

in surface planetary temperatures of the order of 1–10 K. Although this may not sound

like much, temperature changes of this magnitude can have potentially catastrophic effects

on biological systems that have evolved to match very specific environmental conditions,

especially if the rate of temperature change is significantly faster than the rate at which

evolution operates. If significant areas of a planet have average surface temperatures that

643 Exercises for Chapter 13

straddle the freezing point of abundant planetary volatiles (e.g. H

O on Earth, CH

or C

on Titan) temperature variations triggered by changes in one heat transfer parameter may

have profound effects on planetary albedo that amplify the temperature perturbation, both

towards cooling and warming.

Exercises for Chapter 13

13.1 Modify the equations in Section 13.2.1 to include adiabatic temperature change with

elevation. Discuss how this affects the estimate of atmospheric scale height.

13.2 Using the equations in Section 13.2.2 as a guide, derive an approximate expression

for Fe/Mg fractionation in an isothermal planetary magma ocean of composition

(Mg,Fe)

SiO

. Estimate the extent of Fe/Mg fractionation in a 1000-km deep magma

ocean in Earth, Mars and the Moon, assuming T = 1800 K.

13.3 Derive Wien’s law, equation (13.30).

13.4 Derive Stefan–Boltzmann’s law, equation (13.31), and find the value of the Stefan–

Boltzmann constant as a function of Planck’s constant, Boltzmann’s constant and

the speed of light (equation (13.32)).

13.5 Can you suggest a reason why humans do not perceive radiation with wavelengths

longer than about 10 µm as heat?

13.6 Calculate the orbital radius that a planet must have in order to receive the same

energy flux as the Earth from its star (i.e. the solar constant, ∼ 1368 W m

−2

)ifthe

planet orbits:

(i) a red dwarf with T = 2600 K and r = 0.15 r

Sun

(ii) a blue giant with T = 10 000 K and r = 1.7 r

Sun

(iii) a blue supergiant with T = 25 000 K and r = 37 r

Sun

where the stellar radii, r, are given in terms of the solar radius, r

Sun.

Express your

answer in astronomical units and km.

13.7 What is the equilibrium temperature of each of the three planets in 13.6?

13.8 In what section of the spectrum does the electromagnetic energy received by each

of the planets in 13.6 peak? For each of the three planets, discuss the possible nature

of their atmospheres (e.g. are molecules likely to be stable?), the likelihood of life,

and the nature of any possible life.

13.9 Comment on how much a star can conceivably differ from the Sun and still be able

to sustain life as we know it.

13.10 Plot thermalized solar radiation emission flux as a function of heliocentric distance.

Discuss the implications for remote sensing of internal energy flux.

13.11 A Dyson sphere is a stellar engineering project, conceived by the physicist Freeman

Dyson, consisting of an artificial spherical cavity centered on the Sun. Design a

Dyson sphere with an equilibrium temperature of 288 K, assuming that the medium

between the Sun and the internal surface of the sphere does not interact with

electromagnetic radiation of any wavelength.

13.12 Solve differential equation (13.49).

13.13 Solve for the energy fluxes emitted by the ground and by the active atmospheric

layer, F

and F

(Section 13.3.6) using energy balance in the atmosphere rather than

the surface. Compare to equations (13.61) and (13.62).

644 Topics in atmospheric thermodynamics

13.14 Estimate a range of possible surface temperatures for Venus that arise from equations

(13.61) and (13.62). How do these temperatures compare with the observed temper-

ature of the surface of Venus (∼800 K)? Modify the toy model in Section 13.3.6 so

as to include additional terms that might improve the agreement. Comment on your

results.

Thermodynamics of life

In this final chapter we examine life, and in particular how life may have originated, from

a strictly thermodynamic point of view. I will not get anywhere close to biochemistry,

biophysics or genetics, nor will I offer a definition of life. Rather, I begin from a concept

that everybody must agree upon. This is the fact that a necessary (but not sufficient!)

component of the definition of life is that it is a process that never reaches thermodynamic

equilibrium, for if thermodynamic equilibrium is reached then the process stops, and life is

no more. Life must therefore be powered by a gradient in free energy, which for the only

type of life that we know takes the form of a chemical potential gradient, i.e. a non-zero

affinity. Catabolic metabolism (henceforth simply metabolism, as I will not discuss anabolic

metabolism in detail) is a chemical reaction (or rather a set of coupled chemical reactions)

that transfers chemical energy from reactants in an organism’s inorganic environment,

known as the substrate, to complex organic molecules inside the organism, such as ATP

(adenosine triphosphate), that are capable of delivering this energy to structures where the

chemical energy is transformed to mechanical energy (e.g. motion), electrical energy (e.g.

conscience), electromagnetic energy (e.g. fireflies), etc.

Atmospheric composition, and in particular the oxidation state of the atmosphere, is one

of the factors in understanding the origin of life. Strongly reducing atmospheres, rich in

species such as CH

,NH

and H

S, are thought to be best suited for the synthesis of complex

organic molecules. As we shall see, however, an atmosphere with these characteristics may

present near insurmountable obstacles to the establishment of metabolic pathways that

supply energy to living organisms. A somewhat more oxidized atmosphere, in which CO

is an abundant species, is better suited to the inception of catabolic processes. In the first

section of this chapter we use the machinery of fluid equilibrium that we developed in

Chapter 9 to place some constraints on the atmospheric evolution of the terrestrial planets.

14.1 Chemical evolution of post-nebular atmospheres

We seek to understand the chemical evolution of post-nebular atmospheres, i.e. of those

atmospheres that accumulated on rocky planets after loss of the original hydrogen-

dominated nebular atmospheres. The greatest problem that we face in trying to reconstruct

these early environments is that we know very little about the nature of volatile sources

(impactors and/or volcanoes?), their compositions, and the rate of supply of material. We

are also uncertain about the volatile sinks at that time. Thermodynamics provides a way

of analyzing the problem. By constructing a model of speciation in a gas phase we can

examine how the nature of the atmosphere responds to changes in the bulk composition of

the phase, temperature, density and gravitational acceleration.

645

646 Thermodynamics of life

We will use the Gibbs free energy minimization procedure described in Section 9.6.2 and

Worked Example 9.8. The equations and discussion in this section follow closely what we

did there, with a few modifications. We assume a simple atmosphere composed of C, H,

O and N (four system components), and we consider a two-phase system, consisting of a

gas phase in equilibrium with liquid water. The justification for assuming H

O saturation

is that oxygen isotopic compositions of detrital zircons suggest that liquid water existed

on the Earth’s surface as early as 4.2 billion years ago, and perhaps even earlier (Valley

et al., 2005; Valley, 2006). We wish to know what type of atmosphere could have been

in equilibrium with planetary oceans. This is a two-phase four-component system, so it

has four degrees of freedom. We choose to specify temperature and three compositional

variables (concentration of the fourth component follows by difference). Pressure is not

specified a priori, but is rather one of the variables that is solved for, via equation (13.2).

The model ignores dissolution of gas species in liquid water, which may have non-negligible

effects on the calculated gas phase concentrations of fairly soluble species, such as CO

and NH

, but the qualitative trends are almost certainly correct despite this simplification.

Let the total number of mols per unit of planetary surface area of each of the system

components be N

, N

and N

(in atomic proportions, not molecules). Note that

these variables have units of number of mols per unit area, so their values reflect the

total amount of volatile material added to the planet’s surface. We consider the following

chemical species: H

(v apor )

(liquid),

,CO

, CO, N

,NH

and O

, and use

for the number of mols per unit area of species i. Other species that could be present in

small concentrations include formaldehyde (CH

O) and hydrogen cyanide (HCN). We will

show that their concentrations can be reliably estimated a posteriori. In fact, the same is

true of carbon monoxide, but we choose to leave it in the Gibbs free energy minimization

calculation anyway.

The total number of mols of gas species per unit area is given by:

(

vapor

)

. (14.1)

As in Worked Example 9.8, oxygen is not included in (14.1) because its concentration is

vanishingly small, so that it is simpler to write its Gibbs free energy in terms of oxygen

fugacity (equation (9.96), see also below). The pressure at the planet’s surface is given by

equation (13.2), which we expand as follows using (14.1) and molecular weights in kg

atoms:

P =



0.018n

(

vapor

)

+0.002n

+0.0016n

+0.044n

+0.028n

+0.017n



(14.2)

We have four mass balance equations of the type of (9.92), as follows:

=RT



(

vapor

)

+2n

(

liquid

)

+2n

+4n

+3n

−N



=RT



(

vapor

)

(

liquid

)

+2n

−N



=RT



−N



=RT



−N



=0.

(14.3)

647 14.1 Chemical evolution of post-nebular atmospheres

Atmospheric pressures are typically low enough that the ideal gas approximation is perfectly

acceptable. Saturation of the atmosphere in liquid water is therefore given by:

0,H

(

liquid

)

1,T

−

0,H

(

vapor

)

1,T

−lnP −ln



(

vapor

)



=0. (14.4)

We write six partial derivatives of the function Z (equation (9.93)), one each for H

,CO

, CO, N

and NH

. Because we assume ideal gas behavior we omit the fugacity

coefficients from the partial derivatives (compare equation (9.94)). This leads to a consid-

erable simplification in the calculation procedure (Software Box 14.1). The six derivatives

∂Z/∂n

are:

0,H

1,T

+1 +ln P +ln





−

+2λ

0,CH

1,T

+1 +ln P +ln





−

+4λ

+λ

0,CO

1,T

+1 +ln P +ln





−

+2λ

+λ

0,CO

1,T

+1 +ln P +ln





−

+λ

0,N

1,T

+1 +ln P +ln





−

+2λ

0,NH

1,T

+1 +ln P +ln





−

+3λ

+λ

=0.

(14.5)

Software Box 14.1 Speciation calculation in C–H–O–N atmospheres

The Maple worksheet highway_to_hell.mw contains a procedure, atmos, that

calculates speciation in a C–H–O–N gas phase in equilibrium with liquid H

Oatlow

pressure (ideal gas behavior is assumed) by Gibbs free energy minimization. It solves

the system of equations (14.2)to(14.7). The procedure call is as follows.

atmos (T in C, mols H, mols O, mols C, mols N, g in m s

−2

)

Output is sent to the terminal and is self-explanatory. The procedure can be included in

a do loop that varies the input parameters, in order to calculate diagrams such as those

in Figures 14.1 to 14.5.

Thermodynamic data are contained in tab-delimited format in the file aatmosdata,

and also in the spreadsheet sh_data. The order in which the data are to be loaded (row

id numbers) is listed in the heading of procedure atmos.

The error message “Water boiled off” means that a solution of the system of equations

saturated in liquid water was not found. The error message “No convergence” means

that the procedure failed to find a solution within the maximum number of iterations

specified by the variable hmax.