Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

568 Dilute solutions

remains unchanged. The solution must in this case be found by iteration, because in order to

calculate activity coefficients we need to know the ionic strength. A Maple procedure that

does this is described in Software Box 11.2.The calcite saturation reaction (Worked Example

11.4) is handled in an identical fashion, by adding the solubility product equation (11.106)

to the system of equations, calculating the mean ionic activity coefficient of Ca

2−

with (11.131), and using the charge balance equation (11.105).

Software Box 11.2 Calculation of carbonate speciation in aqueous solution. Non-ideal behavior

calculated with Debye–Hückel equation.

Maple worksheet aq_spec_DH.mw contains two procedures, zeco2_DH and

zecalcite_DH, that parallel the procedures in aq_spec_ideal.mw, but add

calculation of aqueous activity coefficients with the Debye–Hückel equation, (11.131)

(see Worked Example 11.5). The Debye–Hückel equations are contained in their own

procedures, at the top of the worksheet. Input for zeco2_DH and zecalcite_DH is

the same as for the equivalent procedures in aq_spec_ideal.mw. Output is also the

same, except that an additional field at the end of each line gives ionic strength.

The soda lake calculations in Worked Example 11.5 are contained in the Maple

worksheet soda_lakes_DH.mw. There are two procedures, soda_lake_Ca and

soda_lake_CO2. The first procedure calculates the composition of the soda lake as

a function of the parameter d

(equation (11.139)) at constant CO

fugacity (see Fig.

11.11). Input is f (CO

) in bar, high d

, low d

, number of intermediate values and

output file name. The output fields are: d

, pH, m

(2+)

HCO

−

(2−)

,Na

bicarbonate ion activity product, Na carbonate ion activity product, ionic strength. The

second procedure performs the same calculations as a function of CO

fugacity at con-

stant d

(Fig. 11.12). Input is low f (CO

) in bar, high f (CO

) in bar, d

, number of

intermediate values and output file name. The output fields are: f (CO

) in bar, pH,

(2+)

HCO

−

(2−)

, Na bicarbonate ion activity product, Na carbonate ion

activity product, ionic strength.

The results of the refined calculations are compared in Table 11.1 to the estimates that we

obtained assuming that the electrolyte solutions were ideal, for a constant CO

fugacity of

3.8 × 10

−4

bar. For rainwater in equilibrium with atmospheric CO

we calculate an ionic

strength of 2.4 × 10

−6

, so the Debye–Hückel equation can be expected to yield accurate

results – in fact, even the limiting law, equation (11.125), would work in this case. Calculated

electrolyte concentrations and pH are virtually indistinguishable from the ideal estimates.

The solution saturated in calcite has an ionic strength of ∼1.8 × 10

−3

, so equation (11.131)

should provide accurate results. In this case pH increases by 0.02 and the concentration

of Ca

increases by about 10% relative to the ideal calculation. These values would be

appropriate for “pure” water in equilibrium which calcite, but not for seawater, which has

an ionic strength about three orders of magnitude higher than what calcite dissolution by

itself generates.

An interesting extension of these calculations is to study the chemical evolution

of soda lakes. These are bodies of water that generally form in closed basins in

arid climates, subject to strong evaporation. The defining characteristic of soda lakes

is that the supply of alkali-earth cations, Ca

and Mg

, is severely limited (see

569 11.6 Activity coefﬁcients in electrolyte solutions

Risacher & Fritz, 1991, 2009; Lowenstein & Risacher, 2009; Millero, 2009; Reimer et al.,

2009). This is the case, for example, if the drainage basin feeding the lake consists predomi-

nantly of felsic volcanic or plutonic rocks. Charge balance of the carbonate and bicarbonate

anions in soda lakes is in such case chiefly accomplished by the alkali cations Na

and

. Evaporation concentrates the solution to the point where carbonates precipitate but,

because sodium and potassium carbonates and bicarbonates are quite soluble, the crystal-

lizing carbonate assemblage typically consists of calcite, magnesite and dolomite. Because

the system is depleted in Mg

and Ca

, however, the pH of soda lakes is not buffered as

effectively as that of seawater, and can in fact reach fairly extreme values. We can construct

a simplified thermodynamic model of a soda lake by considering only the Na

and Ca

cations and carbonate and bicarbonate anions, and writing the following charge balance

equation:

+2m

−m

HCO

−

−2m

2−

−m

−

=0. (11.138)

We seek the values of the six ionic molalities, so we need six equations, one of which

is (11.138). The carbonate and bicarbonate dissociation reactions and the water ionization

reaction are also applicable, so we include (11.133), (11.136) and (11.137). We assume that

the soda lake is saturated in calcite, so we also use equation (11.106). These five equations

do not contain information about the degree of Ca

depletion of the soda lake, yet this

is what defines them and what makes their chemistry so radically different from that of

seawater. We therefore write a final equation that describes the Ca to carbonate ratio, as

follows:

HCO

−

+2m

2−

. (11.139)

A value of d

= 1 means that carbonate and bicarbonate charges are exactly balanced by

. In our simplified model this means that there can be no Na

in solution, but in nature

of course sodium (and potassium) would be present, balanced by other anions such as chlo-

ride and sulfate, as in seawater. If d

< 1 then the soda lake must contain Na

in solution.

We will assume that sodium supply to the lake is unrestricted, so that Na

concentration

in the solution is limited only by the charge balance constraint, equation (11.138).

The six equations: (11.106), (11.133), (11.136), (11.137), (11.138) and (11.139) contain

two free parameters: the fugacity of CO

and the calcium to carbonate ratio, d

. We study

the evolution of soda lakes as a function of these parameters. Numerical solution of the set

of equations with Maple is a straightforward extension of the procedure that we used for the

first part of this example, and is described in Software Box 11.2. Let us assume first that CO

fugacity is fixed by equilibrium with the atmosphere, so we make f (CO

) = 3.8 × 10

−4

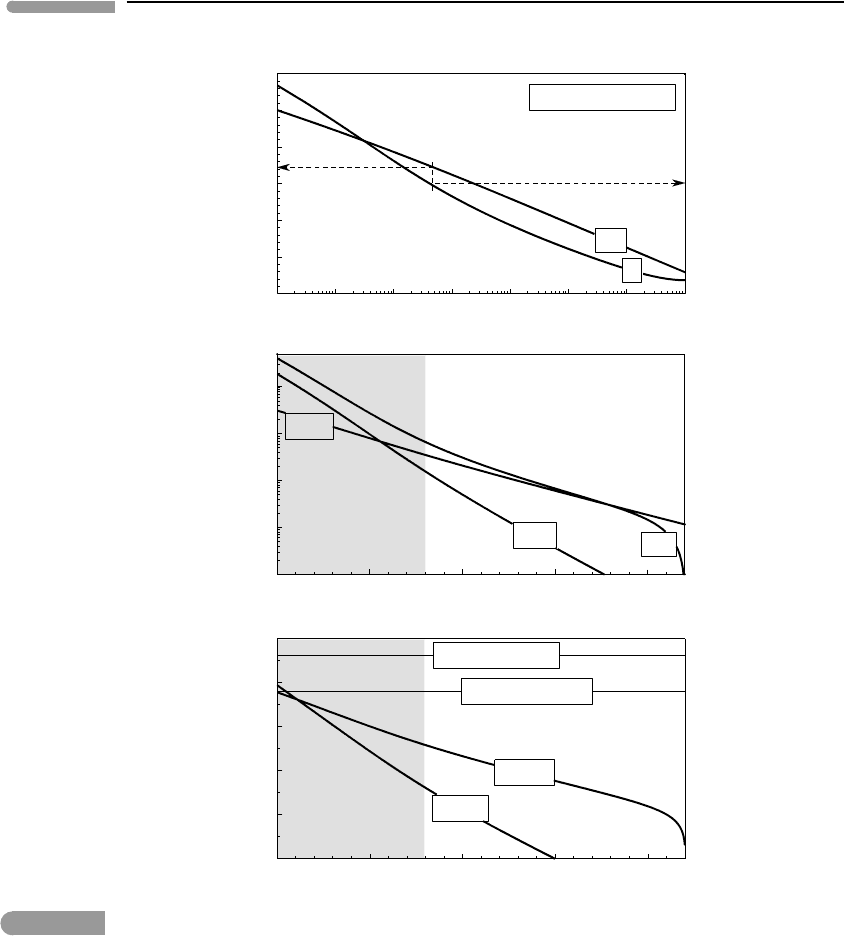
bar. Figure 11.11 shows changes in the chemical composition of the solution as a function

of the calcium to carbonate ratio, d

. The top panel shows pH and ionic strength. For d

=1 we recover the results for seawater, pH ∼8.3 and I ∼10

−3

. Both pH and ionic strength

increase with decreasing Ca

content. At d

∼5 ×10

−5

the pH is about 9.7 and the ionic

strength is about 0.1. The results for our simplified soda lake should be fairly accurate up to

this point, but become less so as Ca

content decreases further and ionic strength increases

(e.g. Fig. 11.10). Ionic strength in real soda lakes is of course much higher, so the results

are not strictly applicable to complex natural systems, but the behavior is qualitatively the

correct one.

570 Dilute solutions

–7

–6

–5

–4

–3

–2

–1

8.0

8.5

9.0

9.5

10.0

10.5

11.0

= 2 m

/(m

HCO

- + 2 m

CO3

)

8.599.51010.5

–4

–3

–2

–1

ion molality

8.599.51010.5

–8

–6

–4

–2

ion activity product

f(CO

) = 380 x10

-6

bar

–3

–2

–1

Ionic strength

HCO

–

NaHCO

saturation

NaHCO

saturation

Fig. 11.11 The chemistry of an idealized soda lake in equilibrium with atmospheric CO

(f (CO

)=3.8×10

−4

bar) at 25

◦

The lake is assumed to contain only Na

and Ca

cations and HCO

−

and CO

2−

anions. Changes in pH and species

distribution are tracked as a function of the Ca

deﬁcit, given by the parameter d

. The pH axes of the center and

bottom diagrams are scaled to correspond approximately to the d

values in the top diagram. The bottom diagram

shows that the ﬁrst sodium species to precipitate is nahcolite (sodium bicarbonate), at pH ≈10.5. The shaded

regions correspond to ionic strengths greater than 0.1 (shown with the dashed arrows in the top diagram),

for which Debye–Hückel theory is not accurate, so the results are only semi-quantitative.

571 11.6 Activity coefﬁcients in electrolyte solutions

The middle panel of the figure shows the molalities of Na

, HCO

−

and CO

2−

ions as a

function of pH , with the pH axis scaled so as to correspond approximately to the values of

the d

parameter in the top panel. The shaded area on the left of the figure corresponds to

the region outside the range of validity of Debye–Hückel theory, i.e. I > 0.1. The dominant

carbonate species changes from HCO

−

for pH <∼10 to CO

2−

for pH > ∼10. All three

ions become strongly concentrated with increasing pH , so one may wonder, do sodium

carbonates precipitate? In order to answer this question we write the saturation reactions:

NaHCO

(

)

 Na

+HCO

−

3aq

(1)

(

)

 2Na

+CO

2−

3aq

(2) (11.140)

and the corresponding equilibrium conditions:

·m

HCO

−



HCO

−



·m

2−



2−

2Na



. (11.141)

In order to determine whether the soda lake becomes saturated in sodium carbonate or bicar-

bonate we compare the values of the equilibrium constants calculated from standard state

thermodynamic properties (the left-hand side of equations (11.141)) with the ion activity

products (the right hand side of the equations) that result from the thermodynamic model

of the soda lake. The values of the equilibrium constants (calculated with standard state

properties from Wagman et al., 1982) are K

= 3.915 × 10

−1

(Na bicarbonate saturation)

and K

= 18.11 (Na carbonate saturation). As long as the ion activity products are smaller

than these numbers the lake is not saturated in sodium carbonates. The bottom panel in Fig.

11.11 shows the values of the ion activity products as a function of pH , as well as the values

of the equilibrium constants. At a constant CO

fugacity of 3.8 × 10

−4

bar the soda lake

trends towards sodium carbonate saturation with decreasing acidity. It becomes saturated

in sodium bicarbonate (the mineral nahcolite) at pH ∼10.5, but at these conditions it is still

far from being saturated in sodium carbonate.

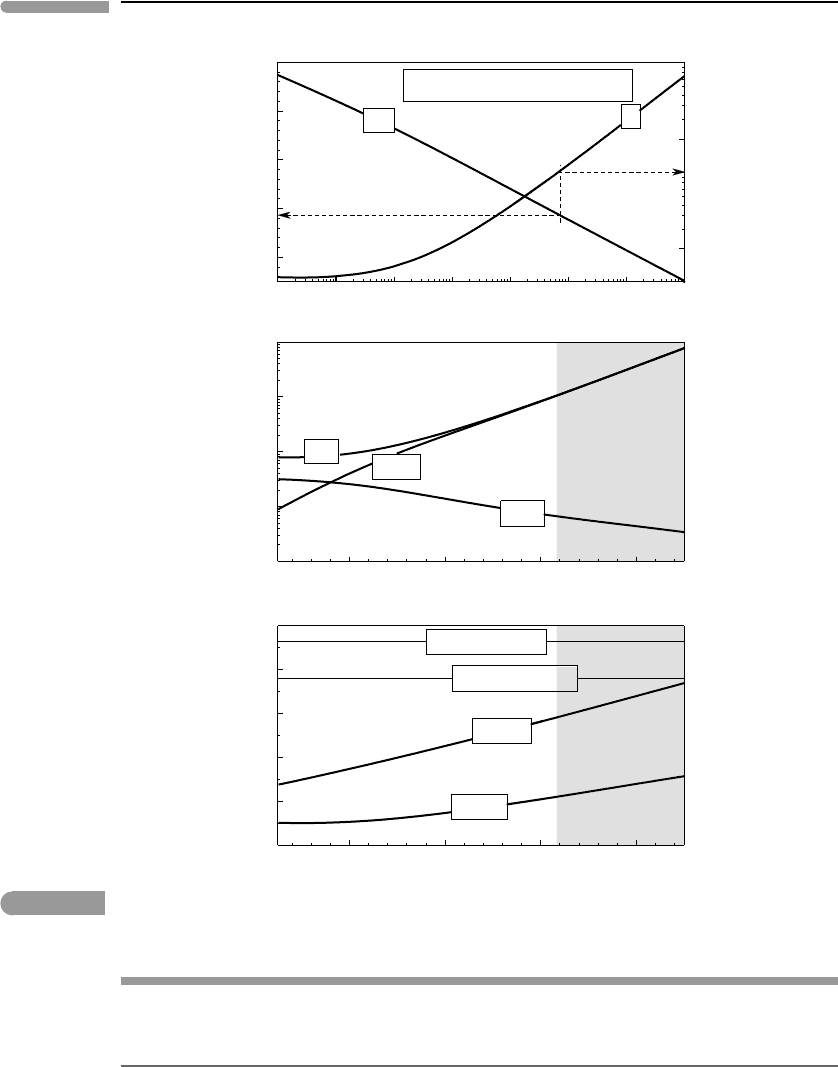
If we keep the calcium to carbonate ratio constant and vary f (CO

) the behavior of

the soda lake is strikingly different. Figure 11.12 shows this, for a constant value of the

parameter d

= 10

−3

. The solution in this case becomes more acidic as it becomes more

concentrated, in response to increasing CO

fugacity. This is opposite to the effectof starving

the lake of calcium at constant CO

fugacity. A consequence of this is that the lake is driven

towards saturation in sodium carbonates with increasing acidity, as can be seen in the middle

and bottom panels of Fig. 11.12. For d

= 10

−3

nahcolite precipitates at pH ∼6.5, which

corresponds to a CO

fugacity of about 10 bar. This result is thermodynamically correct,

but is a consequence of the constraints imposed on this simplified model, in particular the

assumption that an unlimited supply of sodium is available to balance the charge of whatever

carbonate concentration one chooses to apply. There may be few natural environments in

which conditions that allow sodium bicarbonate to precipitate from a mildly acidic solution

are realized. Environments of this kind could exist in lakes formed in craters or calderas of

active felsic and alkaline volcanoes, composed of rocks such as trachytes and pantellerites.

These rocks are rich in alkalis and relatively poor in calcium and magnesium, and volcanic

gases could provide a high CO

flux.

572 Dilute solutions

8.0

7.0

9.0

f(CO

) bar

10.0

11.0

–4

–3

–2

–1

–8

–6

–4

–2

–6

–5

–4

2 m

/ (m

HCO

- + 2 m

2–

) = 10

–3

–2

–1

–2

Ionic strength

ion molalityion activity product

NaHCO

saturation

NaHCO

saturation

98710

98 7

HCO

–

Fig. 11.12 Same as Fig. 11.11, but tracking changes in the soda lake as a function of CO

fugacity, for a constant value of d

0.001. The behavior of the soda lake is remarkably different. Precipitation of nahcolite takes place in this case in

response to increasing acidity. This may occur in response to inﬂux of CO

-rich volcanic gases.

11.6.2 Activity coefficients in concentrated electrolyte solutions

That the complete Debye–Hückel equation, (11.131), is not accurate for solutions with

ionic strengths greater than ∼0.1 has been known since the equation was proposed. Debye–

Hückel theory, however, performs well for dilute solutions, in which key assumptions,

such as treating the solvent as a continuum (i.e. assuming that the macroscopic dielectric

constant is valid) and ignoring all characteristics of the ions beyond their charge and radius,

573 11.6 Activity coefﬁcients in electrolyte solutions

can be expected to be better approximations than in concentrated solutions. This suggests

that equation (11.131) encapsulates important aspects of the behavior of real electrolytes,

and that concentrated solutions may be amenable to be described by extensions of Debye–

Hückel’s theory. Two such theories are widely used to study natural systems. One of them,

due to Pitzer and co-workers, is largely based on calibrating non-ideal empirical interaction

parameters among individual ions. The other one, proposed by Helgeson and collaborators,

seeks to preserve the Debye–Hückel philosophy as much as possible, by identifying the

species that form by ion association, defining their standard state properties as a function

of temperature and pressure, and accounting for the effects of temperature and pressure on

the dielectric properties of the solvent. Both formulations lead to equations of significant

operational complexity (as opposed to mathematical complexity), the full development of

which is beyond the space available here. Excellent summaries of the contrasting Pitzer

and Helgeson approaches, as well as of a few other simpler alternatives, can be found in

the textbooks by Anderson (2005) and Nordstrom and Munoz (1986).

The formulation of Pitzer and co-workers starts with the limiting law of Debye and Hückel

and expands the excess Gibbs free energy of mixing, beyond the amount that is accounted

for by Debye–Hückel theory, as a virial-like, but largely empirical, series in composition.

Philosophically this is the same approach used in the Pitzer and Sterner equation of state

(Section 9.4.4). The earliest attempt along these lines is due to Guggenheim (1935; 1967,

p. 286), who suggested a characteristically simple and clever approach. His idea was based

on the fact that, because the Debye–Hückel equation is chiefly (or only, for the limiting law)

a function of solvent properties and ionic strength, different solutes of the same charge type

(and approximately the same ionic size) should have the same excess chemical potential in

any solution of the same ionic strength. This is not what is observed. Guggenheim proposed

that some arbitrarily defined and well-characterized electrolyte, for example NaCl, be used

as a reference, and that one then measure the difference in the excess Gibbs free energy

of mixing of other electrolytes relative to that of the standard. He then suggested that

the difference in excess Gibbs free energy of mixing between an arbitrary solution and a

solution of pure standard electrolyte be expanded as a sum of terms, each of which has the

form β

, where m

and m

are cation and anion molalities, and β

is an empirical

interaction parameter that characterizes each cation–anion pair. Guggenheim did not include

terms for interactions between ions with the same charge. This is known as the principle

of specific ion interactions and was first stated by Brønsted (1922) who hypothesized that

ions of the same charge never come close enough together to have an effect on the free

energy of the solution beyond that which arises from their charge (i.e. their identity does not

matter). This may be true in dilute solutions, but not in concentrated ones. By differentiating

Guggenheim’s expression for excess Gibbs free energy of mixing one obtains expressions

for the osmotic coefficient (equation (11.36)) and activity coefficients (equation (11.13)),

relative to those of the standard. The properties of the standard electrolyte are given by the

Debye–Hückel theory. These will not be accurate in absolute terms, but since the activity

coefficients for all electrolytes are referred to this same standard the differences among

them can be expected to reproduce the observed behavior fairly well.

Pitzer’s approach is an extension of these ideas, differing in three important ways: (i) the

binary interaction terms contain more than one empirical parameter, which are functions of

ionic strength (Guggenheim’s β

is a constant, except perhaps for an unknown temperature

dependency), (ii) interactions between ions of the same sign are included, and (iii) triple

particle interactions, which may be negligible in dilute solutions but not at high concentra-

tions, are also included. Pitzer’s general equation for the excess Gibbs free energy of the

574 Dilute solutions

solution has the form:

(

)



(

)



ij k

, (11.142)

where w

is the mass of solvent (in kg), f (I ) is a function of ionic strength and solvent

properties that is similar, but not identical, to the Debye–Hückel equation (11.131), and

the n

, n

are number of mols of ionic species. The interaction parameters λ

(I) are a

function of ionic strength, they include more than one adjustable parameter, and they apply

to interactions among same charge as well as opposite charge ions, and neutral species

too if they exist. The ternary interaction parameters µ

ij k

, on the other hand, are not a

function of ionic strength and are set to zero if all three ions are of the same charge.

Equation (11.142) is manipulated so as to express the interaction parameters as functions

of measurable electrolyte properties, and the resulting expression differentiated relative to

or m

in order to obtain the osmotic coefficient of the solvent or the activity coefficient

of each solute (equations (11.13) and (11.36)). The details, which are rather ponderous,

canbefound,forexample,inPitzer(e.g.1987,1995),andthefinalequationsarealso

summarized by Anderson (2005). Important applications of Pitzer’s equations include to

terrestrial evaporites (see Harvie & Weare, 1980; Harvie et al., 1984) and ocean water (see

Millero, 2004, 2009, and references therein), Martian brines and evaporites (see Chevrier

& Altheide, 2008; Chevrier et al., 2009; Marion et al., 2003, 2008, 2009), and icy-satellite

cryomagmas (Marion et al., 2005).

Pitzer’s model is calibrated at 298 K and 1 bar. Extrapolation to other conditions is accom-

plished by expressing the interaction parameters as polynomial functions of temperature

and pressure, although at present these functions are calibrated for only a relatively small

set of electrolytes of geological importance (see, for example, Marion et al., 2008). An

important aspect of the model, which is expressed in equation (11.142), is that it assumes

that interactions occur among individual ions. If a specific ionic association (i.e. species

formation) takes place this is not considered explicitly but is rather reflected in the values

of the interaction parameters, which generate a lower activity coefficient for the affected

ions. The model is therefore purely thermodynamic, in the sense that it focuses only on

macroscopic properties, regardless of what the microscopic mechanism for these properties

may be.

Helgeson’s approach (see Helgeson, 1969; Helgeson et al., 1981; Tanger & Helgeson,

1988) differs significantly from Pitzer’s in this last respect. Ion association and complex

formation are explicitly accounted for. Infinite dilution standard state properties are gen-

erated for all species, together with heat capacity and volumetric data. This allows a more

straightforward extrapolation to high temperatures and pressures. In fact, at high tempera-

ture Helgeson’s model is physically more satisfactory than Pitzer’s, because the decrease in

the dielectric constant of water with increasing temperature, that limits electrolyte dissocia-

tion, is explicitly accounted for (all electrolytes at high temperature tend to behave as weak

electrolytes). Speciation calculations in Helgeson’s model are accomplished by writing

chemical reactions among the species and solving for the species concentrations that make

the Gibbs free energy change of all the homogeneous equilibrium reactions vanish (this

is equivalent to the chemical equilibrium approach to fluid speciation, see Section 9.6.1).

Activity coefficients are based on the Debye–Hückel model, complemented by empirical

species-specific terms. The computational details are intricate and are nicely summarized

by Anderson (2005).

575 Exercises for Chapter 11

Exercises for Chapter 11

11.1 Integrate (11.41) in two different ways, so as to obtain (11.42) and (11.43).

11.2 Study various pathways for the formation of ClO

(chlorine peroxide gas), e.g. from

various combinations of the elements in their molecular and atomic states, as well as

from the respective hydrides (HCl and H

O). What are likely pathways for formation

of perchlorates in planetary atmospheres? What makes these reactions possible (i.e.

where is the “missing free energy” coming from?) What are likely constraints on the

types of natural environments where perchlorates can form? Necessary thermody-

namic properties can be obtained from Wagman et al. (1982) or NIST’s Chemistry

WebBook.

11.3 Show that the equations derived in Section 11.2.3, that lead to the relations between

activity and osmotic coefficients, equations (11.41) through (11.43), are also valid

for electrolyte solutions, using bulk electrolyte properties.

11.4 Modify the Maple procedure used to calculate carbonate speciation in rainwater (Fig.

11.5) to include calcite saturation equation (11.106).

11.5 Study the distribution of ferric species in aqueous solution as a function of pH

at some constant value of oxygen fugacity that is high enough to make concen-

trations of ferrous species negligible (e.g. the present day terrestrial atmosphere).

Find the conditions under which Fe

becomes the dominant aqueous species.

Discuss how analytical Fe

concentration varies with pH at constant oxygen

fugacity. How would your conclusions be affected by changes in oxygen fugac-

ity, as long as its value is oxidizing enough to suppress ferrous species? What is

the likely significance of primary hematite deposits, i.e. hematite that precipitated

from aqueous solution directly, without formation of intermediate metastable ferric

hydroxides?

11.6 Discuss why, although possible, it is unlikely that most terrestrial BIF’s formed in

response to a change in oceanic pH, and that a change in oxidation conditions is the

simplest and most probable explanation.

11.7 Show that in an atmosphere as reducing as f (O

) ∼10

−70

bar the concentration of

carbon monoxide is negligible relative to that of carbon dioxide, so that CO

is the

dominant oxidized carbon species. If the atmosphere was also saturated in H

O, could

concentration be significant at this oxygen fugacity? A review of Chapter 9 can

be useful. We will discuss these calculations in greater detail in Chapter 14.

11.8 Modify the Maple procedures discussed in Software Box 11.1 to include saturation in

both calcite and siderite. The calculation must include the Fe

hydrolysis reaction,

equation (11.122). Assume an ideal aqueous solution. Plot the concentrations of the

various aqueous ferrous species, and total Fe

analytical concentration as a function

of pH . Assume that oxygen fugacity is low enough to make Fe

concentration

negligible.

11.9 Write a Maple procedure that calculates Debye–Hückel osmotic coefficients, by

integrating (11.131) according to (11.43).

11.10 Study the phase relations of saturation of calcite, dolomite and magnesite from aque-

ous solution as a function of dissolved Mg

and Ca

concentrations, atmospheric

concentration and temperature. Write the necessary Maple procedures, using

Debye–Hückel activity coefficients. Your calculations are not applicable to seawater

576 Dilute solutions

(why?), but are the results likely to be reasonably accurate for a simple solution like

the one you are modeling? Molalities of Mg

and Ca

in present-day ocean water

are ∼0.053 and 0.010, respectively (from Millero, 2004). What carbonate should

one expect to precipitate according to the simplified model? How does this compare

with carbonate precipitation from seawater? Discuss your findings.

Non-equilibrium thermodynamics and rates of

natural processes

With the exceptions of Chapters 2 and 3, our discussions have largely focused on equi-

librium conditions, and chiefly on the equilibrium of systems in which the only kind of

mechanical work that takes place is expansion work. Even with these severe restrictions

thermodynamics can provide a wealth of information about the nature and evolution of

planetary bodies. But these are by no means the limits of thermodynamics. In fact, one

could argue that thermodynamics only begins to get interesting when these restrictions are

lifted.An in-depth discussion of the possibilities that open up would demand an entire book,

at least as long as this one. That is a fight for another day. The goal of this chapter is to

lift a corner of the proverbial veil. I will introduce some of the principles of linear non-

equilibrium thermodynamics and use them to examine chemical diffusion and chemical

reaction mechanisms and rates. These are two classes of processes that are responsible for

displacing systems towards equilibrium in a wide range of situations.

12.1 Non-equilibrium thermodynamics

By definition, equilibrium thermodynamics concerns itself with static systems and with

“quasi-static” transformations between equilibrium states. These are abstractions, but if

our discussions so far are any indication, they are very useful ones. Throughout the pre-

vious chapters we have also come across non-equilibrium processes, however. Examples

include catastrophic planetesimal collisions (Chapter 2), heat transfer (Chapter 3) and non-

isentropic melting (Chapter 10). Processes such as these are the purview of non-equilibrium

thermodynamics. I will present here a short introduction to non-equilibrium thermodynam-

ics of systems close to equilibrium (the precise meaning of this will become clear in an

instant), along the lines initiated by de Donder, Onsager, Mazur, Prigogine, de Groot and

collaborators (see, for example, de Donder, 1936; de Groot, 1959; de Groot & Mazur, 1984;

Prigogine, 1961, 1962, 1967; Prigogine & Defay, 1965). This topic is not only intellectually

exciting, but it also provides the framework that underlies processes as apparently distinct

as heat and mass diffusion, the progress and rate of chemical reactions, viscous deformation

and electrical currents.

12.1.1 Fundamental concepts

We begin by revisiting our definition of entropy (Chapter 4). Let us split the entropy change

of a system into an external part, d

S and internal part, d

dS = d

S +d

S. (12.1)

577