Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

538 Dilute solutions

Worked Example 11.2 Perchlorate brines on the Martian surface

The chemical experiments aboard the Phoenix spacecraft, that reached Mars in May of

2008, detected what appears to be a large concentration of the perchlorate ion, ClO

−

, in her

landing site on the planet’s northern plains (Hecht et al., 2009; Kounaves et al., 2009). The

importance of this finding is that alkali- and alkali-earth perchlorates are quite soluble in

water. The maximum freezing point depression of a solution (i.e. its eutectic temperature)

depends in part on the location of the solubility curve ad in Fig. 11.2 (given by equation

(11.58)) – the more soluble a solid is, the lower the eutectic temperature is likely to be. The

question arises, could perchlorates be soluble enough, and abundant enough on Mars, to

extend the stability field of liquid water to the conditions of the Martian surface? And why

would perchlorates be so abundant on Mars in the first place? Formation of perchlorates

requires an oxidant more powerful than molecular oxygen (Exercise 11.2). The most likely

explanation for its presence on Mars, and in some desert terrestrial environments, is the

oxidation of chloride anions in the atmosphere, either by ozone or by some of the products

of ozone photochemistry (Catling et al., 2010; see also Chapter 12).

The calculation of the eutectic point of an aqueous solution entails the simultaneous

solution, for temperature and solute molality, of equations (11.49) and (11.58). The melting

and solubility curves, ba and ad in Fig. 11.2, are then constructed by solving each of these

equations for one of the variables (e.g. temperature) as a function of the other (molality). The

procedure is in principle the same one that we used to calculate eutectic phase relations in

Chapter 6, and that we implemented inSoftware Box 6.1. The phasediagrams for magnesium

perchlorate and sodium perchlorate aqueous solutions were calculated in this manner by

Chevrier et al.(2009). For solutions of electrolytes the calculations are far from trivial,

however. This is so because, as we shall see later in this Chapter, the activity and osmotic

coefficients of electrolyte solutions are rather complex functions of composition. We will

therefore not repeat the calculations of Chevrier et al.(2009), but will rather study their

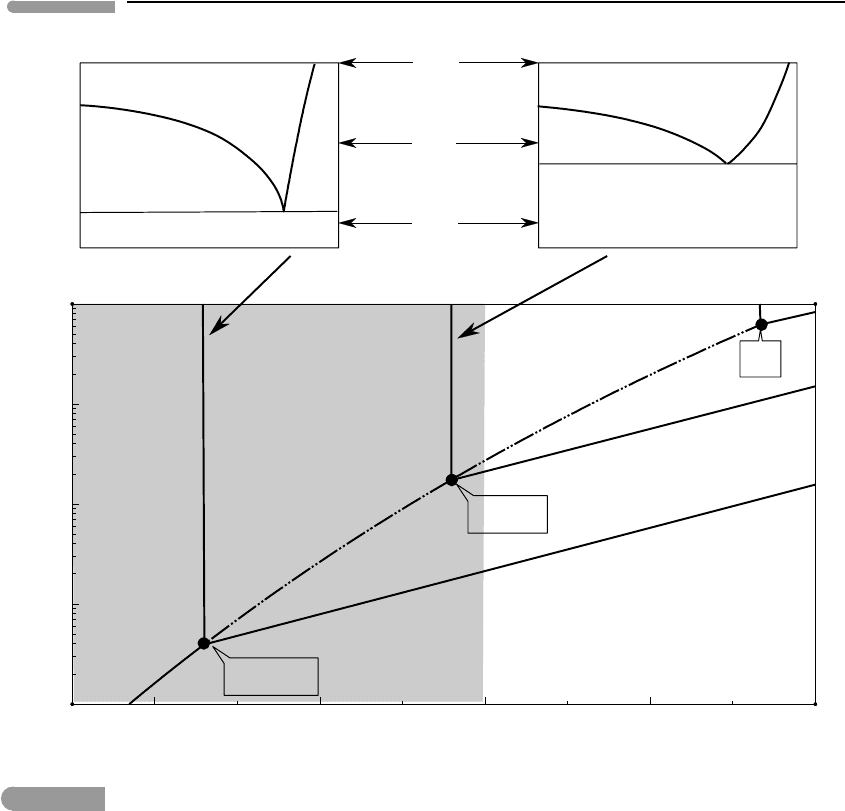
phase diagrams, from which I extract the diagrams at the top of Fig. 11.3.

Chevrier et al. found that the system Mg(ClO

)

–H

O has a 1-bar eutectic temperature

of 206 K, and that the concentration of magnesium perchlorate in the eutectic melt is 44

wt%. The corresponding values for the system NaClO

–H

O are 236 K and 52 wt%. These

temperatures must lie on the vapor-absent curves of the respective binary systems, such

as a or f in Fig. 11.2. We can construct the vapor-absent curves by assuming that their

slope is the same as that of the freezing curve of pure H

O. This is not rigorously true,

as both the entropy and volume of the solutions will in general be different from those

of pure liquid water (recall that dP /dT = S/V , and that ice is a pure phase in all

cases). The error that might be introduced between 1 bar and the near zero pressure of

the Martian surface is, however, almost certainly negligible. The bottom diagram in Fig.

11.3 shows the P–T locations of the vapor-absent equilibria, which are the Mg-perchlorate

and Na-perchlorate eutectics, inferred from the temperatures calculated by Chevrier et al.

(2009) and the Clapeyron slope of the freezing reaction of pure H

O. Also shown is the

ice sublimation curve, calculated from the H

O data of Wagner et al.(1993). Since this is

the liquid-absent curve its location is independent of the composition of the solution. The

intersection of each of the freezing curves with the sublimation curve defines the invariant

point for each system (the invariant point for pure H

O is also shown for comparison). A

third phase boundary, the boiling curve, emanates from each invariant point. These curves

are shown schematically, as their slopes remain unknown.

539 11.2 Effects of dilute solutes

200 220 240 260 28

0.001

0.01

0.1

Temperature(K)

Pressure (mbar)

300 K

250 K

200 K

wt% Mg(ClO

)

wt% NaClO

brine

brine + ice

ice + perchlorate

brine

prc.

br.

prc.

206 K

236 K

52 wt%

44 wt%

Mg perchlorate + ice

Na perchlorate + ice

Na perchlorate + vapor

Mg perchlorate + vapor

liquid

vapor

ice

2,NaClO

2,Mg(ClO

)

Fig. 11.3 Melting phase relations for the binary systems Mg(ClO

)

–H

O and NaClO

–H

O (top), simpliﬁed from Chevrier et al.

(2009). The corresponding P–T phase relations for the two systems are shown in the bottom diagram. Compare

Fig. 11.2.

The P–T diagram in Fig. 11.3 corresponds to a system in which no additional volatile

components are present, so that the partial pressure of H

O in the vapor phase is equal to

the total pressure on the system. The Martian atmosphere, however, consists predominantly

of components other than H

O, so the partial pressure of H

O in the gas phase is much

lower than atmospheric pressure, which is about 7 mbar at the planet’s mean surface level.

The diagram can nevertheless be applied to understand conditions on the Martian surface,

if we keep the following in mind. The freezing curve is a vapor-absent equilibrium so it

is not affected by changes in the composition of the vapor phase. Its P–T location remains

unchanged whether the pressure axis represents total pressure or partial pressure. The boiling

and sublimation curves represent equilibrium between vapor and condensed phases, and

the condensed phases will not undergo any significant change in volume in response to

pressure differences of order 1 bar or less. Therefore, the location of the phase boundaries

540 Dilute solutions

within the restricted range of conditions shown in the figure depends only on the partial

pressure of H

O, and we can think of the pressure coordinate as representing this variable,

rather than atmospheric pressure.

The shaded region in the diagram shows a range of possible surface conditions on Mars.

Martian surface temperatures are within the range in which perchlorate brines can exist.

Whether such brines are thermodynamically stable depends on the H

O content of the

Martian atmosphere. In the Mg-perchlorate system the liquid can be stable down to an

O partial pressure of ∼0.003 mbar, which would correspond to an H

O mol fraction of

∼10

−4

in the Martian atmosphere. The values for the Na-perchlorate system are ∼0.2 mbar

O partial pressure, equivalent to an H

O mol fraction of about 0.03. For comparison, the

saturation vapor pressure of pure H

Oat298Kis∼31 mbar, so that 100% relative humidity

in the terrestrial atmosphere at this temperature corresponds to an H

O mol fraction of about

0.03. The corresponding mol fraction value at 273 K is ∼0.006.

The minimum atmospheric H

O concentration required to stabilize Na perchlorate brine

is almost certainly higher than anything that is common, or even possible, in the Martian

atmosphere, but Mg perchlorate brines might be stable in unusually “humid” Martian envi-

ronments. We can speculate that stable perchlorate brines probably do not exist over most

of the surface of Mars. Chevrier et al.(2009) showed, however, that evaporation rates of

metastable brine pools could be slow enough that they could persist for a few hours. Even

if long-lived pools of stable perchlorate brines did exist on Mars, however, it is not clear

what their biological significance might be, given that perchlorates are powerful oxidizers

(Chapter 14).

11.3 Electrolyte dissociation

A very important class of dilute solutions are electrolyte solutions. These are solutions in

which the solutes dissociate, partially or fully, into electrically charged mobile species,

or ions. The evidence that this happens is the higher electrical conductivity of electrolyte

solutions compared to that of the pure solvent. The thermodynamic treatment of electrolyte

solutions is based on the general formulation for dilute liquid solutions that we developed

in Sections 11.1 and 11.2, but includes some significant extensions.

Athermodynamic description of electrolyte solutions should be independent of anymicro-

scopic model of the solution, but it will be helpful to have in mind at least a rudimentary

microscopic model. In fact, accurate prediction of excess mixing properties in electrolyte

solutions is impossible without recourse to their microscopic properties. Let us begin with

a simple question: why do substances dissociate into ions? This happens when the thermal

energy of the ions, of order k

T , becomes comparable to the work that must be performed to

separate them. In an ionic solid the forces holding the atoms together are purely electrostatic.

Therefore, an ionic solid will dissociate into ions either if the thermal energy increases or

if the electrostatic attractive forces decrease. The former case corresponds to melting and

gives rise to what is called a pure liquid electrolyte, i.e. a liquid made up of free anions and

cations. Molten alkali halides are the archetypal examples of this (see also Section 10.1).

Alternatively, electrostatic attractive forces may decrease as a result of interactions with

the molecules of the solvent. Dissociation in this case occurs at temperatures at which the

substance would otherwise be a solid. The result is the formation of an electrolyte solution.

541 11.3 Electrolyte dissociation

11.3.1 The dielectric constant and the structure of polar liquids

We recall Coulomb’s law, equation (1.38), that gives the magnitude of the electrostatic force

between two charged particles:

4π/

||q

. (11.62)

The constant / is a material property called the permittivity, except if the charges are located

in vacuum, in which case it is a universal constant called the permittivity of free space and

symbolized by /

. For all substances it is found that />/

. We define a non-dimensional

quantity ε

, called the dielectric constant, as the ratio:

> 1. (11.63)

From (11.62) it follows that the dielectric constant is also a measure of how much the

electrostatic force decreases in response to the introduction of a material between charged

particles. The higher the dielectric constant, the lower the electrostatic force, everything

else being equal.

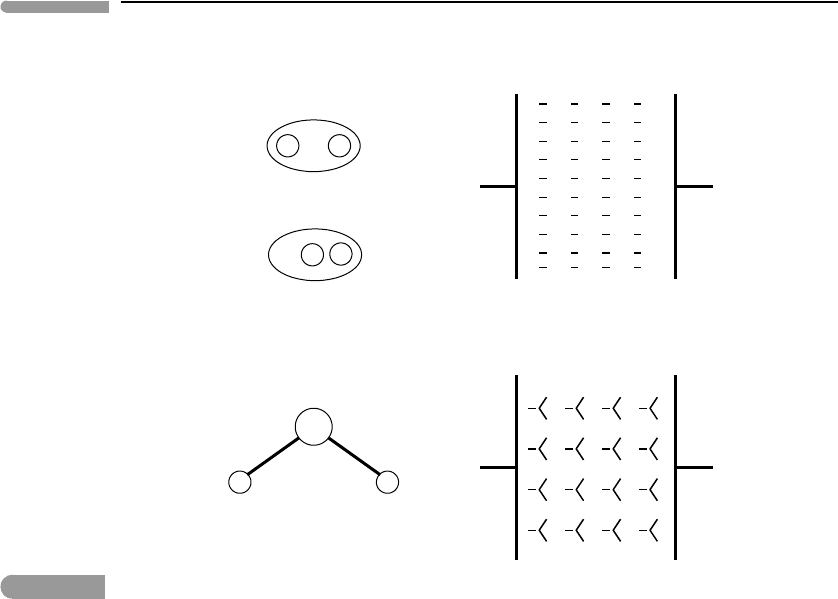
The physical explanation of this behavior is easy to see. Consider two oppositely charged

plates, initially separated by a vacuum (Fig. 11.4). By (11.62), intercalation of an insulating

substance between the plates decreases the electrostatic force between them. The decrease

in the electrostatic force happens because all substances become polarized to some extent.

What this means is that the electric field between the plates causes the charge distribu-

tion in the interstitial material to become asymmetric, such that there is some excess of

negative charge closer to the positive plate, and an equal excess of positive charge closer

to the negative plate. These charge excesses generate an induced electrostatic field that

opposes the primary field between the plates, and hence lowers the net attractive force

between them. Of course, if the substance is an electrical conductor (i.e. if the potential

difference between the plates is higher than its dielectric strength, see Worked Example

1.4) then current will flow, the plates will lose their charge, and this picture is no longer

valid.

Non-polar materials consist of molecules with symmetric charge distribution. In the

absence of an external field the molecules do not display any preferred charge distribution, or

in other words, they are not polarized.When a non-polar substance is immersed in an electric

field, however, it acquires induced polarization as described in the last paragraph. The

magnitude of the induced field that opposes the primary field depends on the characteristics

of the individual molecules and on their density. In diatomic elemental gases at low pressure

(low molecular density) the induced field is extremely weak. Hence, their dielectric constant

may be indistinguishable from 1 for most practical purposes. For instance, the dielectric

constant of dry air at 298 K and 1 bar is ∼1.0005, so that the force between charged particles

immersed in air is virtually indistinguishable from what the force would be in vacuum. In

non-polar liquids, such as hydrocarbons or liquid CO

, the dielectric constant is somewhat

higher (typically of order 2), largely as a result of the higher molecular density, which

engenders a stronger induced field.

In contrast to non-polar substances, polar materials consist of molecules with an inherent

charge asymmetry that exists regardless of the presence of an external electrostatic field.

Water is both an excellent example and the most important one in the planetary sciences.

The two OH bonds in H

O subtend an angle of ∼105

◦

. Because the bonds arise from

542 Dilute solutions

–

+ +

– +

+ –

Polar molecule

Non-polar molecule

No field

In field

Fig. 11.4

Schematic diagram comparing the behavior of a non-polar substance (top) with that of a polar substance (bottom). In

the absence of an external electric ﬁeld charges in the molecules of non-polar substances are distributed

symmetrically, but the symmetry is broken when an external ﬁeld is applied (right). Polar substances such as water

have molecules with permanent charge asymmetry, that acquire a preferred orientation in an external ﬁeld. In both

cases an induced electric ﬁeld appears that opposes the external ﬁeld, but this ﬁeld is much stronger in polar

substances. Because thermal agitation tends to disrupt molecular orientation the intensity of the induced ﬁeld (and

the dielectric constant) decreases with increasing temperature.

sharing of the H electrons, each of the two H ends of the molecule acquires a fractional

positive charge, and the O vertex the complementary negative charge. When H

O molecules

are immersed in an electric field between charged plates the molecules orient themselves

such that the negatively charged vertices face the positive plate and the positively charged

ends the negative plate. The result is a strong induced field and therefore a large decrease

in the electrostatic force between the plates. For example, the dielectric constant of H

at 298 K is ε

r,H

= 78.3, meaning that the force between charged particles immersed

in water is almost two orders of magnitude less than in vacuum. The dielectric constant

varies inversely with temperature. Its value for liquid water at 1 bar is 87.7 at the freezing

point and 55.7 at the boiling point. It decreases further at higher temperatures, in liquid

water kept from boiling by increased pressure, and in supercritical H

O. This behavior

is to be expected from the simple fact that increasing thermal agitation tends to disrupt

the molecular orientation responsible for the induced field that opposes the external field.

Other polar liquids generally have dielectric constants comparable to or lower than that of

water. For instance, liquid ammonia has a dielectric constant of 22 at its 1 bar boiling point

(239.7 K).

543 11.3 Electrolyte dissociation

11.3.2 Free energy of ions in dielectric materials

At an intuitive level we can think of ionic dissociation in polar solvents as taking place

because the dielectric constant of the solvent lowers the attractive force between ions in

the crystal to the point where thermal agitation is able to break the electrostatic bonds.

The problem with this simple model is that it considers the solvent to be a structureless

continuum, when in reality it is made up of molecules of comparable size to the ions of the

solute. The dielectric constant is a macroscopic property, so that its value cannot be expected

to remain unchanged down to molecular lengthscales. In spite of this, the continuum model

for the solvent forms the basis of what was historically the first successful physical model

for electrolyte solutions, proposed by the great German physicist Max Born in the early

1920s. Born’s model seeks to calculate the change in free energy that takes place when

an isolated ion is transferred from vacuum to a material. The result provides fundamental

physical insight into the nature of electrolytic dissociation, so we will reconstruct the main

aspects of Born’s reasoning.

First we need to define the electrostatic potential, Φ

. As for gravitational potential, this

is defined as the electrostatic potential energy per unit of electric charge. From equation

(1.47)weget

4π/

, (11.64)

where q is the electric charge that engenders an electric field in a medium of permittivity /,

and Φ

is the electrostatic potential at a distance r from the charge. Note that the potential can

be positive or negative, depending on the sign of the charge. Born’s idea is to consider ions

as spheres of radius r

that are initially electrically neutral, and calculate how much energy

is required to charge the sphere with the electric charge of the ion, q

. This energy equals the

work, w

, done against the electrostatic field by the charging process. The energy, which is

stored in the field as electrostatic potential energy, is given by the following integral:



dq =

4π/r



qdq =

4π/r

. (11.65)

The procedure is somewhat analogous to calculating the gravitational binding energy of

a body (Section 2.4), but there is a crucial difference. This is that, whereas gravitational

assembly of a body always extracts potential energy from the gravitational field, charging a

body stores energy in the electrostatic field, because work must be performed to overcome

the electrostatic repulsion between the charge already present in the body and the newly

arriving charge increment. The square in q

in equation (11.65) ensures that w

is always

positive, whether the charge of the ion is positive or negative.

We recall from Section 4.8.4 that, if energy transformations other than heat exchange,

expansion work and transfer of chemical components take place in a system, then their

contributions must be included in the thermodynamic potentials. Charging a sphere at

constant temperature, pressure and composition therefore changes its Gibbs free energy by

an amount 

G equal to w

, or:



G =

4π/r

. (11.66)

As always with Gibbs free energy, what we are interested in is not its absolute value, but

rather how its value changes between different states of a system. In this case we ask, how

544 Dilute solutions

does the Gibbs free energy of an ion differ between a state in which the ion is in vacuum

and another state in which the ion is immersed in a material with dielectric constant ε

Calling this Gibbs free energy difference 

G, we see that it is given by:



G =

(



)

material

−

(



)

vacuum

4π/r

−

4π/

(11.67)

which, simplifying and introducing the definition of the dielectric constant (equation

(11.63)), becomes:



G =

4π/



−1



< 0. (11.68)

This is known as Born’s equation, and it packs a physics punch in a beautifully compact

expression. First, because for all materials the dielectric constant is greater than 1, the Gibbs

free energy change is always negative. Thus, an isolated ion is always more stable if it is

immersed in a solvent than if it is in vacuum. Moreover, the tendency for an ion to enter

solution becomes stronger (i.e. 

G becomes more negative) the greater the dielectric

constant of the solvent is. This says that electrolyte solutions form more readily the more

polar a solvent is. For a given solvent, as temperature increases and the dielectric constant

decreases electrolytic dissociation becomes less likely. Born’s equation also shows that the

tendency towards electrolytic dissociation varies directly with the square of ionic charge

and inversely with ionic radius.

By differentiating (11.68) one can obtain an expression for the enthalpy change associated

with immersing an ion into a solvent. With some additional algebraic manipulations and

reference state conventions (see below) this enthalpy becomes an experimentally accessible

quantity. Experimental measurements show that, although Born’s equation is a brilliant

conceptual model, it is not quantitatively successful, as it predicts enthalpies of solution

that are generally too high by a factor of ∼2. The failure is to a significant extent due to the

fact that the macroscopic dielectric constant is not valid at the range typical of molecular

interactions. The presence of a charged ion must affect the local arrangement of molecules

in a polar solvent, and therefore the local value of its dielectric constant. For example,

a cation in liquid water surrounds itself with a sheath of H

O molecules arranged with

their oxygen vertices towards the cation. This structure is known as a solvation sphere

(hydration if the solvent is water), and the number of solvent molecules attached to the ion

as the solvation (or hydration) number. Solvation causes the effective dielectric constant at

molecular lengthscales to be lower than the macroscopically determined value.

11.4 Thermodynamic formulation of electrolyte solutions

It is possible to distinguish two contrasting behaviors among electrolytes. There are

electrolytes that undergo complete dissociation, meaning that there is no evidence that

undissociated molecules exist in the solution. These are called strong electrolytes. The

classic examples of these are alkali halides in aqueous solution at room temperature, and

in particular NaCl. On the other hand, there are electrolytes, called weak electrolytes,

that undergo only partial dissociation, such that ions coexist in the solution with neutral

undissociated molecules. Room temperature aqueous solutions of weak acids and of many

545 11.4 Thermodynamic formulation of electrolyte solutions

transition metal salts behave in this way. The distinction is not invariable. For example,

some electrolytes are fully dissociated at low concentrations and only partially dissoci-

ated as concentration increases. The nature of the solvent also plays a fundamental role,

as described by Born’s equation (equation (11.68)). A substance may behave as a strong

electrolyte in a solvent with a high dielectric constant, and as a weak one if the solvent’s

dielectric constant is lower. In particular, substances that behave as strong electrolytes in

liquid water at room temperature become weak electrolytes, or fail to dissociate altogether,

in high temperature liquid water and supercritical H

O. The thermodynamic treatment of

the two types of electrolytes differs in the definition of the standard states and of quantities

that depend on the standard state, such as activity and activity coefficient.

11.4.1 Thermodynamic functions of ionic species

We begin by discussing general thermodynamic relations that are the same for all types of

electrolytes. The standard state thermodynamic properties of ionic species are defined as in

Section 11.1.2, at the infinite dilution limit (equation (11.7)), which, as we saw, can also be

thought of as a hypothetical one-molal ideal solution. In the case of ionic species there is an

additional restriction, which is that the solution must be electrically neutral. The condition

of electrical neutrality of an electrolyte solution is written as follows:



=0, (11.69)

where m

is the molality of ion i and z

is its charge, positive or negative depending on

whether it is a cation or an anion. Even if a solution contains many different ions, it will

be convenient to consider anion–cation pairs that correspond to dissociation of specific

electrolytes. Take for instance an ionic substance composed of anions A−, of charge z

A−

and cations B+ of charge z

B+

, and let the formula unit of the substance be B

, such that:

βz

B+

+αz

A−

=0. (11.70)

Dissociation of the substance corresponds to the reaction:

 β

(

B+

)

+α

(

A−

)

. (11.71)

This equation is valid regardless of whether the substance is a strong or weak electrolyte. I

have specified the state of the ionic species by means of the subscript aq, meaning aqueous

solution. All of the equations that we will develop here are valid for any polar solvent, but

since liquid H

O is the most common one in natural environments we will use “aqueous”

as a generic designation. If we were to consider solutions in liquid ammonia, for instance,

then am could replace aq as the subscript. Note that, in contrast to the ionic species, I have

not specified the state of the compound B

in equation (11.71). This will take different

meanings in strong and weak electrolytes. For now we are only concerned with the ionic

species, and equation (11.71) is in this sense best thought of as an algebraic identity, not as

a chemical reaction.

We write the chemical potentials of the ionic species as follows:

B+

= µ

0,B+

+RT ln a

B+

A−

= µ

0,A−

+RT ln a

A−

(11.72)

546 Dilute solutions

where the standard state chemical potentials correspond to the usual infinite dilution limit.

The electrical neutrality constraint (equation (11.69)) introduces the complication that con-

centrations of individual ions cannot be varied independently of those of opposite charge.

As we shall see later this is solved by arbitrarily assigning a value of zero to the standard

state properties of the cation H

The ionic activities in equations (11.72) are given by:

B+

=γ

B+

A−

=γ

A−

(11.73)

The B–A ion pair appears in the proportions β to α in every equilibrium equation involving

the compound B

. This makes it convenient to define the mean ionic molality, m

, and

mean ionic activity coefficient, γ

, of dissociated electrolyte as follows:



(

B+

)

(

A−

)



β+α

(11.74)

and:





B+





A−





β+α

(11.75)

The three following points need to be emphasized. First, the mean ionic molality and mean

ionic activity coefficient correspond specifically to electrolyte B

. Second, equation

(11.74) does not imply that the molalities of B

and A

−

in the solution are in the propor-

tion β to α. This would be the case only if the solution was one of pure electrolyte B

In a mixed electrolyte solution the relative amounts of the ions are only constrained by the

bulk charge balance condition (11.69), and will in general not correspond to the stoichio-

metric coefficients β and α. However, the mean ionic molality and activity coefficient for

electrolyte B

are still given by (11.74) and (11.75). Third, for reasons that will become

apparent in the following section we have not defined a “mean ionic activity” analogous to

the mean ionic molality and activity coefficient.

11.4.2 Standard states and activities of strong and weak electrolytes

A solution of a weak electrolyte contains undissociated molecules, which we shall label

)

, as well as ions. For equilibrium among the aqueous species:





 β

(

B+

)

+α

(

A−

)

(11.76)

it must be:

=βµ

B+

+αµ

A−

. (11.77)

We can also write (11.77) as:

βµ

0,B+

+αµ

0,A−

−µ

0,B

+RT ln K

=

P ,T

+RT ln K

=0, (11.78)

547 11.4 Thermodynamic formulation of electrolyte solutions

where 

P ,T

is the standard state Gibbs free energy change for the dissociation reaction

(11.76) at infinite dilution and the temperature and pressure of interest, so that:

=exp



−



P ,T



. (11.79)

The equilibrium constant K

is known as the dissociation constant and is also equal to:



B+





A−



. (11.80)

Because in the case of a weak electrolyte the species (B

)

exists, its standard state

properties are defined in the same way as those for any other molecular or ionic dilute

solute (equation (11.7)). In this case the molality of the undissociated solute is a physically

significant quantity. We can then write the activity of the undissociated electrolyte in terms

of its molality and activity coefficient, as follows:

=γ

(11.81)

and using the mean ionic molality and mean ionic activity coefficient of the dissociated

species (equations (11.74) and (11.75)) we get the following expression for the dissociation

constant:





β+α

. (11.82)

In contrast to weak electrolytes, when a strong electrolyte dissolves in a polar solvent

it undergoes complete dissociation. If this is the case then the molecular species (B

)

is not present in the solution, and one cannot specify its molality. As we shall see, it is

nevertheless convenient to define thermodynamic properties for a fictive species that we

can call the bulk aqueous electrolyte, (B

)

. We can give a precise thermodynamic

definition of (B

)

by stating that, if B

is a strong electrolyte and Y stands for any

of the thermodynamic potentials, the entropy, the heat capacity or the volume of the bulk

aqueous electrolyte, then Y is given by:

≡βY

B+

+αY

A−

. (11.83)

Thus, the chemical potential of (B

)

is:

≡βµ

B+

+αµ

A−

. (11.84)

Note that there is a subtle difference with equation (11.77), for a weak electrolyte: whereas

in that case the equation is the statement of chemical equilibrium, equation (11.84), for

a strong electrolyte, is the definition of the chemical potential of the fictive bulk species.

Expanding (11.84) in terms of standard state chemical potentials and activities we find:

0,B

+RT ln a

=β



0,B+

+RT ln a

B+



+α



0,A−

+RT ln a

A−



. (11.85)