Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

528 Dilute solutions

Worked Example 11.1 Concentration of atmospheric gases in Earth’s oceans

Henry’s law constants and their temperature dependency can be calculated from standard

state thermodynamic properties and activity coefficients but, more commonly, they are

measured directly. Comprehensive tabulations exist for virtually all gases in aqueous solu-

tion (Sander, 1999; also NIST Chemistry WebBook). These tables typically list values of

A,0

H ,s

and (−

/R), the latter parameter commonly labeled as (d ln K/d(1/T )). A sim-

ple application of equations (11.18) and (11.23) is to calculate the concentration of gases

dissolved in liquid H

O in equilibrium with the terrestrial atmosphere. Figure 11.1 shows

equilibrium molalities of N

, Ar and CO

as a function of temperature, calculated with

constants and temperature derivatives from Sander (1999). The fugacities are assumed to

be constant and equal to 0.8 bar, 0.2 bar, 0.01 bar and 3.8 × 10

−4

bar, for N

, Ar and

respectively (the latter figure assumes an atmospheric CO

concentration of 380 ppm

by volume, and is likely to be a nostalgic value by the time you read this). As expected, all

concentrations decrease with increasing temperature, but the temperature dependency of

concentration is stronger than those of the other gases. This is one of several positive

feedback mechanisms in global warming: as the oceans warm they exsolve CO

, which

further raises its atmospheric concentration. Warming oceans also become depleted in oxy-

gen, and the change could be significant for organisms that may have evolved very specific

metabolic requirements or oxygen exchange mechanisms.

The molalities shown in the figure correspondto the concentrations of the actual molecular

species. For nitrogen, oxygen and argon these are likely to be essentially the same as the

total dissolved concentrations (=analytical concentrations) of the corresponding gases. For

this is not the case, as CO

reacts with H

O to form H

,which in turn dissociates

into protons and carbonate and bicarbonate anions. The analytical concentration of CO

seawater is thus greater than the concentration of molecular CO

calculated from Henry’s

law (Worked Example 10.4).

5101520253

–5

–4

–3

Temperature (°C)

Molality

Molecular gas species in aqueous solution

Fig. 11.1 Concentration of atmospheric gases dissolved in water in equilibrium with the terrestrial atmosphere. Calculated with

Henry’s law constant data from Sander (1999). The plot shows the concentration of the molecular species only.

529 11.2 Effects of dilute solutes

11.1.5 Nernst’s distribution law and trace element partitioning

Although the focus of this chapter is on liquid solutions, and in particular aqueous solutions,

it is instructive to take a short detour and revisit the trace element partitioning equations

that we discussed in Section 10.3. Consider a solute i in two dilute solutions with different

solvents, s1 and s2. Let the corresponding chemical potentials of the solute be µ

and µ

At equilibrium we have µ

= µ

, or:

0,i

+RT ln



i,s1



=µ

0,i

+RT ln



i,s2



. (11.24)

Rearranging:

i,s1

i,s2

i,s1

exp



0,i

−µ

0,i



. (11.25)

This equation, known as Nernst’s distribution law, is the same relationship that we derived

in Chapter 10 to describe trace element partitioning between minerals and melt (equation

(10.13)). The two standard state chemical potentials are the chemical potentials of the same

trace component, at infinite dilution in two different solvents. At constant temperature,

therefore, the exponential factor is a constant. If we consider a restricted compositional range

then the activity coefficients may also be approximately constant, and we recover (10.13),

with the right-hand side of equation (11.25) equal to D, the partition coefficient. Note that

we have not specified the aggregation state of the two solvents. Nernst’s distribution law

is equally valid for crystal–liquid partitioning as it is for partitioning between two different

crystals, or two different liquids.

Writing the distribution law in the form of equation (11.25) one can examine some of

the complications underlying the modeling of trace element behavior in igneous systems.

First, the partition coefficient is a function of temperature. Temperature variability within

a given type of magmatic system (e.g. basalts) may be restricted enough that it can be

safely ignored, but the same is not true if we compare, for example, basaltic and rhyolitic

systems. Second, melts with significantly different major element compositions (consider

again basalts vs. rhyolites) effectively behave as different solvents, so that the standard

state chemical potential of the same trace element will be different in each solvent, and so

will the partition coefficient. Third, the activity coefficients are in general functions of the

composition of the solvent and of the concentrations of all the solutes, so if we once again

consider the example of basalts vs. rhyolites we see that the activity coefficient for the same

solute will almost certainly be different, and so will the partition coefficient.

11.2 Effects of dilute solutes on the properties of the solvent

Dilute solutes can have strong effects on the behavior of the solvent, such as depressing its

freezing point, raising its boiling point, or affecting its density and refractive index. We now

look at the equations that make it possible to track some of these effects. All of the equations

in this section are valid in general, for both molecular and electrolyte solutions, although

as we shall see in later sections electrolyte solutions require additional considerations.

530 Dilute solutions

11.2.1 The osmotic coefficient

We can write the Gibbs–Duhem equation (equation (6.6)) for a dilute solution at constant

temperature and pressure as follows:

dµ



dµ

=0. (11.26)

Dividing by n

∗

we get:

∗

dµ



dµ

=0. (11.27)

If all of the solutes behave ideally (i.e. γ

=1 for all is) then from (11.8) we get:

dµ

(11.28)

so:

∗

dµ

+RT



=0. (11.29)

Integrating to the composition of the solution:

RT M

∗



=µ

0,s

−µ

s,ideal

, (11.30)

where µ

0,s

is the standard state chemical potential of the solvent (pure solvent at the

temperature and pressure of interest) and µ

s,ideal

is the chemical potential of the solvent in

the ideal dilute solution. The sum



is the total concentration (molality) of dissolved

species.

Equation (11.30) is true only if all of the solutes dissolve ideally, which is in general not

the case. In order to account for the aggregate excess mixing behavior of all the solutes one

defines a parameter φ, called the osmotic coefficient, as follows:

φ ≡

0,s

−µ

RT M

∗



(11.31)

from which we get the chemical potential of the solvent (compare equation (11.30)):

=µ

0,s

−RT M

∗



. (11.32)

The osmotic coefficient φ is a function of the molality of each solute, m

, and of the

contribution of each solute to the excess mixing properties of the solution. Calculation of

an explicit value is generally far from trivial, but if a value can be measured or calculated

then equation (11.32) yields the chemical potential (and other thermodynamic properties)

of the solvent.

531 11.2 Effects of dilute solutes

11.2.2 Osmotic coefficient and excess Gibbs free energy of the solution

The chemical potential of the solvent, µ

s,ideal

, in equation (11.30) corresponds to an ideal

solution, whereas µ

in equation (11.32) is that of a real solution. The excess chemical

potential of the solvent, µ

s,ex

=µ

−µ

s,ideal

, is therefore given by:

s,ex

(

1 −φ

)

RT M

∗



. (11.33)

If one has an explicit formula for the excess Gibbs free energy of the solution, G

, then

the osmotic coefficient can be calculated as follows. From equation (5.28):

s,ex



∂G

∂n



P ,T ,n

(11.34)

where n

is the number of mols of solvent, and n

are the number of mols of solutes, which

remain constant. Equating (11.33) and (11.34):

1 −φ =

RT M

∗





∂G

∂n



P ,T ,n

. (11.35)

When working with aqueous solutions it is common, however, to measure the mass of the

solvent in kg rather than in number of mols. If the mass of n

mols of solvent is w

, then

∗

and (11.35) becomes:

1 −φ =





∂G

∂w



P ,T ,n

. (11.36)

Equation (11.36) is the starting point for the calculation of osmotic coefficients in electrolyte

solutions (Section 11.6).

11.2.3 Relationship between osmotic coefficient of the solvent and activity

coefficients of the solutes

Differentiation of (11.8) for a non-ideal solution yields:

dµ

∂γ

∂m

(11.37)

substituting in (11.27) and simplifying:

∗

dµ

+RT



+RT



∂γ

=0. (11.38)

Differentiating (11.31) we find:

dµ

=−RT M

∗





dφ +φ





. (11.39)

532 Dilute solutions

Substituting in (11.38) and simplifying:

(

1 −φ

)



−dφ +



d ln γ

=0, (11.40)

which for a solution of a single solute simplifies to:

d ln γ =

(

φ −1

)

+dφ. (11.41)

Depending on whether one wishes to calculate the activity coefficient of the solute from the

osmotic coefficient of the solvent, or vice versa, and recalling that, because the infinitely

dilute solution is assumed to be ideal, we have γ = φ = 1asm → 0, we can integrate

(11.41) in one of two ways (Exercise 11.1):

ln γ =φ −1 +



φ −1

dm (11.42)

or:

φ =1 +



md ln γ . (11.43)

Solving the integrals requires either measured values of one of the variables over a con-

centration range extending to very dilute solutions (m → 0), or an explicit equation for the

activity coefficient or osmotic coefficient as a function of composition (Section 11.6).

11.2.4 Freezing and boiling of dilute solutions

One application of osmotic coefficients is to predict how phase transitions of the solvent

are affected by the presence of dilute solutes. We shall use the melting point depression

equation (6.49) once more. Consider a liquid solution that freezes to pure solid solvent

(aqueous solutions behave in this way to an excellent approximation). For this case we

write equation (6.49) as follows:

ln a

liq

=−





−

0,f



, (11.44)

where a

liq

is the activity of the solvent in the liquid solution, 

is the enthalpy of melting

of the solvent and T

0,f

is the freezing temperature of the pure solvent at the pressure of

interest. From equation (11.32) we see that:

ln a

liq

−µ

0,s

=−M

∗



. (11.45)

Substituting (11.45)in(11.44) we find:

−

0,f

∗





. (11.46)

If we now assume that T remains close to T

0,f

we can simplify (11.46) as follows:

T = T

0,f

−

∗

0,f





. (11.47)

533 11.2 Effects of dilute solutes

The first factor in the second term in the right-hand side of equation (11.47) contains

properties of the solvent only – its non-dimensional molecular weight, enthalpy of melting

and freezing temperature – and the gas constant R. It is therefore a constant for each solvent,

which is known as the cryoscopic constant, k

∗

0,f



. (11.48)

For H

O at 1 bar the values of the parameters in equation (11.48) are: T

0,f

= 273.15 K,



= 5.94 kJ mol

−1

, and M

∗

= 0.01802, which yield k

cr,H

= 1.882 K (P = 1 bar).

Note that the cryoscopic constant is always a positive quantity, as enthalpy of melting is

always positive. Therefore, a solution that freezes to pure solvent always does so at lower

temperature than the pure liquid solvent. This is of course the same behavior that we found

for eutectics in igneous systems (Chapters 6 and 10). We can also re-write (11.47) more

simply as:

T = T

0,f

−k



, (11.49)

emphasizing the fact that for a given solvent the magnitude of the freezing point depression

depends on the total molality of solutes and on the osmotic coefficient (which is a sort of

“aggregate activity coefficient”).

If the solutes can be considered to be non-volatile compared to the solvent, i.e. if their

vapor pressures are negligible compared to that of the solvent, then when the solution

boils the vapor phase is composed to a very good approximation of pure solvent. Aqueous

solutions of solid solutes generally behave in this way. The boiling point displacement

caused by the presence of non-volatile solutes can also be calculated with equation (6.49).

According to the labeling convention adopted at the beginning of Section 6.5.1 regarding

the placement of the high-entropy phase we now write equation (6.49) as follows:

ln a

liq





−

0,b



. (11.50)

As before, a

liq

is the activity of the solvent in the liquid solution, but now 

is the

enthalpy of vaporization of the solvent and T

0,b

is the boiling temperature of the pure

solvent at the pressure of interest. Following the same sequence of steps used in deriving

equation (11.47) we arrive at:

T = T

0,b

∗

0,b





. (11.51)

The ebullioscopic constant, k

, comprises only properties of the solvent and is defined as:

∗

0,b



. (11.52)

The parameters for H

O at 1 bar are: T

0,b

= 373.15 K, 

= 40.6 kJ mol

−1

, and

∗

= 0.01802, yielding an ebullioscopic constant k

eb,H

= 0.514 K (P = 1 bar). Because

the enthalpy of vaporization is always a positive quantity it must be k

>0. Therefore,

it follows from (11.51) that a solution always boils at higher temperature than the pure

534 Dilute solutions

solvent. Because the osmotic coefficient φ is in general a function of temperature its value

in equations (11.47) and (11.51) will in general be different, even for solutions with the

same total solute molality,



11.2.5 Solubility of a pure solute

Equations (11.47) and (11.51) describe the equilibrium of a dilute solution with pure solid

solvent and pure solvent vapor, respectively. It is also of interest to describe the equilibrium

between the solution and a pure solute. The composition of the solution along this equi-

librium defines the solubility of the solute in the specific solvent. At equilibrium between

solution and pure solute we have:

=µ

0,i(s)

, (11.53)

where µ

is the chemical potential of the solute in the solution and µ

0,i(s)

is the standard

state chemical potential of pure solute at the pressure and temperature of interest. Note very

carefully that this is the chemical potential of the pure solute, which could be a solid, liquid

or gas, as opposed to the chemical potential of an infinitely dilute solute in the solvent of

interest, which we label µ

0,i

(cf. equation (11.7)). Substituting equation (11.8)in(11.53)

and rearranging we arrive at:





0,i(s)

−µ

0,i

. (11.54)

Let us now define the molar Gibbs free energy of dissolution at infinite dilution, 

follows:



=µ

0,i

−µ

0,i(s)

. (11.55)

Substituting in (11.54) and taking the temperature derivative:

∂ ln





∂T







, (11.56)

which simplifies to:

∂ ln





∂T



, (11.57)

where 

is the molar enthalpy of dissolution at infinite dilution. Note that the value of



depends on both the solute and the solvent and that, in contrast to the enthalpies of

melting and vaporization, it may be a positive or a negative quantity (or, conceivably but

very unlikely, zero).

We can integrate (11.57) between some convenient reference temperature T

(e.g. 298 K)

and any arbitrary temperature T. After some simplification, and assuming that we can make

≈ T

, we arrive at:

i,0



i,0



exp





(

T −T

)



. (11.58)

535 11.2 Effects of dilute solutes

This equation yields the solubility of the solute in the solvent as a function of temperature

(at constant pressure), assuming that we know the solubility at some reference temperature

and an equation for the activity coefficient as a function of temperature and composition.

If 

>0, i.e. if dissolution is endothermic, then solubility varies directly with temper-

ature, and conversely, it varies inversely with temperature if dissolution is exothermic and



<0.

11.2.6 Expansion of the stability field of liquid water by dilute solutes

Water may be the only common liquid solvent in which chemical reactions associated

with biological metabolism can take place (Chapter 14). For this reason it is of interest to

understand how the presence of dilute solutes expands the stability field of liquid water. In

Worked Example 6.5 we used Schreinemakers’ rule to derive a schematic phase diagram

for the system H

O–NaCl. The qualitative results, summarized in Fig. 6.12, are applicable

to aqueous solutions of non-volatile solids in general, regardless of whether or not they

are electrolytes. We saw in that example that Schreinemakers’ rule causes the solute-absent

and solute-present invariant points to be located along the liquid-absent curve in relative

positions such that freezing and boiling of brine occur at lower and higher temperatures,

respectively, than the corresponding phase transitions for pure H

O. This is what equations

(11.47) and (11.51) require. We can now include some additional information that is missing

from Fig. 6.12.

Consider an aqueous solution, which we will label liquid, of a generic non-volatile solid.

In most cases of geological interest the solute will be an electrolyte. We study such solutions

beginning in the next section, but what we are interested in here is in the behavior of the

solvent, and this can be discussed in general terms without specifying the nature of the solute.

As far as the solvent is concerned the details of the solute are encapsulated in the osmotic

coefficient, which is what determines the behavior of the solvent.

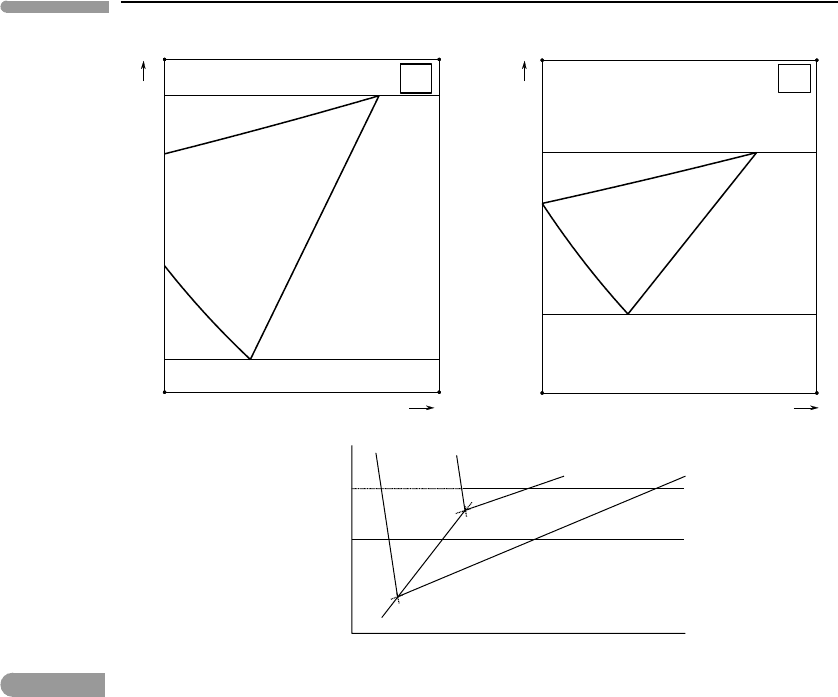
The pressure–temperature phase diagram shown at the bottom of Fig. 11.2 is redrawn from

Fig. 6.12. Invariant point O

corresponds to the pure H

O system, whereas O

corresponds

to the H

O–salt binary system. The two diagrams at the top of the figure are isobaric

temperature–composition sections at two pressures, P

and P

, above and below the pressure

of invariant point O

. We will assume that there are no other volatile components in the

system, so that the partial pressure of H

O in the vapor phase is equal to the total pressure.

The diagrams are schematic, however. The composition axes are calibrated in molality

and extend from pure H

O to some unspecified solute molality somewhat higher than the

saturation concentrations. For virtually all solutes of interest in the planetary sciences this

would correspond to solute mol fractions much smaller than 1.

At pressure P

pure H

O freezes and boils at the temperatures of points b and c, respec-

tively. Addition of a solute shifts the freezing point to lower temperature (equation (11.47))

and the boiling point to higher temperature (equation (11.51)). The graphs of these two

functions in the temperature–composition diagram are the freezing and boiling curves, ba

and cd, which show the composition of liquid in equilibrium with pure H

O ice and pure

O vapor, respectively. Each of the divariant assemblages (pseudo-univariant at constant

pressure), liquid + ice and liquid + vapor, exists inside the field labeled accordingly, with

the liquid composition given by the intersection of the temperature coordinate with the cor-

responding bounding curve. The liquid becomes saturated in solid at points a and d. At each

of these two points three phases are stable, so they must be located on the corresponding

univariant phase boundaries for the solute-bearing system, as shown in the bottom diagram.

536 Dilute solutions

liquid

liquid + solid

liquid+solid

liquid

ice

liquid

ice

liquid+vapor

solid + vapor

solid + ice

(V) (V)

(I)

(L, S)

Fig. 11.2

Freezing and boiling phase relations of dilute aqueous solutions of a non-volatile solute. The P–T phase diagram

(bottom) is redrawn after Fig. 6.12. The two isobaric temperature–composition phase diagrams (top) correspond to

pressures higher and lower than that of the triple point of pure H

O(O

). The liquid ﬁeld shrinks continuously from

the pressure of point O

to the pressure of point O

, where it disappears altogether.

They must also appear as pseudo-invariant points on the isobaric sections. Because a and

d are saturation points they must both lie on the solubility curve given by equation (11.58).

The graph of this function is therefore the curve ad in the figure. The divariant assemblage

liquid + solid is stable to the right of the curve, with the composition of the solid-saturated

liquid given by the intersection of the temperature coordinate with curve ad. Note that inside

the field labeled “liquid” only one phase is stable, so that the assemblage is trivariant, or

pseudodivariant at constant pressure. Temperature and liquid composition can be chosen

independently as long as no other phase is stable.

Equations (11.47) and (11.51) assure us that, because points a and d are saturated in

solid, they must correspond to the minimum freezing temperature and maximum boiling

temperature at pressure P

. Point a is therefore a eutectic (compare with Figs. 6.21 and 6.23).

For all temperatureslower than that of a the system consists of the divariant assemblage ice+

solid. Similarly, in a neighborhood above the temperature of point d the stable assemblage

is solid +vapor, but this divariant field must terminate at some higher temperature, at which

the solid melts.The eutectic and maximum boiling temperatures can be calculated by solving

simultaneously equations (11.47) and (11.58), or (11.51) and (11.58), respectively.

537 11.2 Effects of dilute solutes

Consider now the temperature–composition phase relations at pressure P

, lower than

that of the triple point of pure H

O (invariant point O

).At pressure P

pure liquid H

O is not

stable, so the liquid + vapor and liquid + ice fields must meet at the H

O composition end-

member. This happens at point g, which corresponds to a point along the stable univariant

sublimation curve for H

O (see bottom figure). As in the previous case, the freezing and

boiling curves, gf and gh, are the graphs of functions (11.47) and (11.51). They map the

liquid compositions in equilibrium with ice and vapor, respectively, and terminate at points

f and h on the solubility curve, given by equation (11.58). As pressure decreases from

to O

the temperatures of the eutectic point, f , and of the maximum boiling point, h

approach each other, so that the temperature interval within which liquid is stable shrinks.

The two temperatures become identical, and equal to the sublimation temperature, at O

For pressures lower than that of O

liquid is never stable and the only possible univariant

equilibrium in the two-component system is the degenerate H

O sublimation reaction.

There is a subtle point that we must address. In deriving equations (11.47) and (11.51)we

assumed that the pure liquid solvent is stable, and therefore that freezing and boiling of the

pure solvent take place. For pressures between O

and O

liquid is stable only if it contains

dissolved solutes in it, so that freezing and boiling of the pure solvent do not take place.

Is it then “legal” to use equations (11.47) and (11.51) to construct the freezing and boiling

curves? Moreover, what temperatures should be chosen for T

0,f

and T

0,b

, the freezing and

boiling point of the pure solvent? The graphical construction in Fig. 11.2 suggests that

both temperatures should be the same, and equal to the sublimation temperature of the

solvent at the pressure of interest. We now demonstrate formally that this is indeed the case.

Equilibrium along the freezing curve can be written as (see equation (11.32)):

liquid

=|µ

0,H

liquid

|−RT M

∗



=µ

0,H

ice

, (11.59)

where the standard state chemical potential of liquid H

O enclosed inside vertical lines

is a fictive value, corresponding to a hypothetical pure liquid H

O phase at pressure P

Similarly, for the boiling curve we have:

liquid

=|µ

0,H

liquid

|−RT M

∗



=µ

0,H

vapor

. (11.60)

The two curves meet at the pure H

O end-member (point g), at which



= 0, so:

0,H

ice

=µ

0,H

vapor

=|µ

0,H

liquid

|. (11.61)

The sublimation temperature (g in the figure) therefore corresponds to both the (fictive)

freezing and boiling temperatures of pure H

O. Moreover,the fictive standard state chemical

potential of liquid H

O is well defined, and is equal to the standard state chemical potentials

of ice and vapor at the sublimation temperature. This makes it possible to define the activity

of H

O in liquid as in equation (11.45), and thus confirms that functions (11.47) and (11.51)

represent the freezing and boiling curves of liquid at pressures below the triple point of pure

O too.