Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

498 Melting in planetary bodies

Temperature

Pressure

solid

melt

solid + melt

p,m

solidus = liquidus

mantle adiabat

melt adiabat

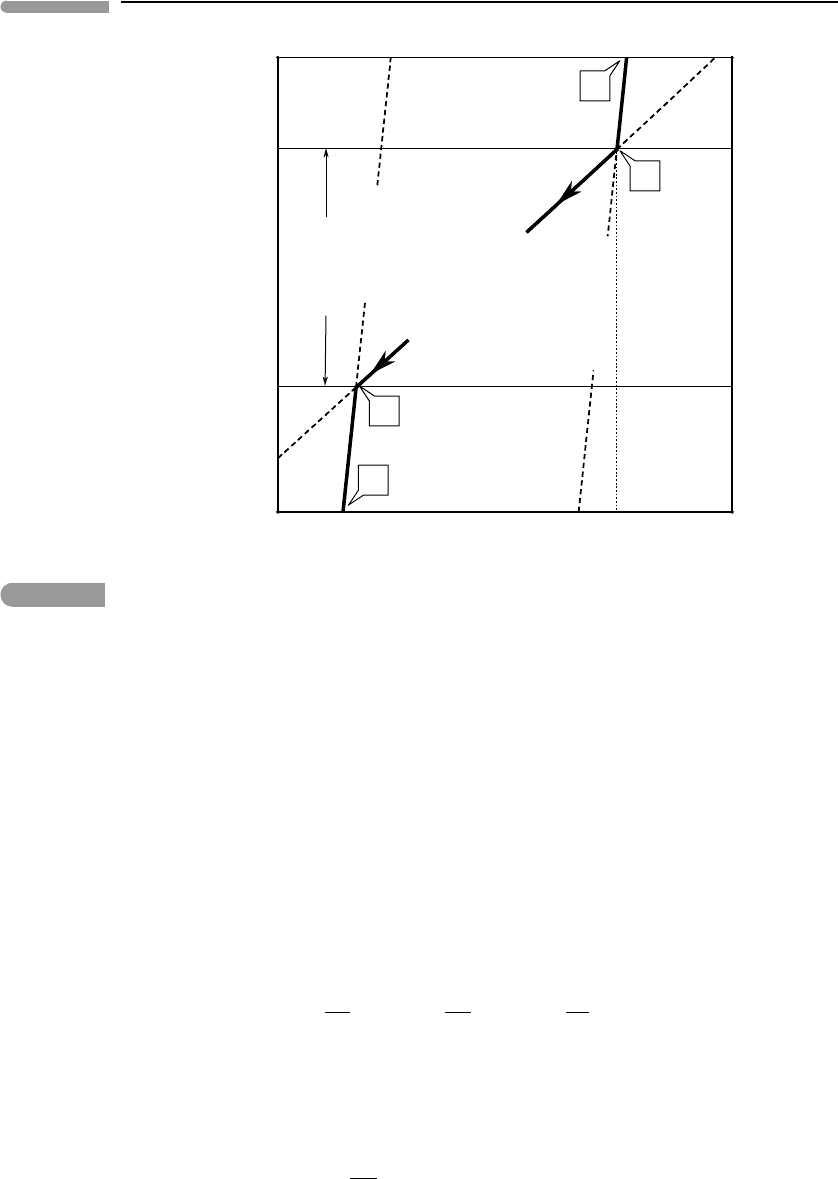
Fig. 10.8

Decompression melting of a one-component system. The solid mantle (divariant in a one-component system) rises

adiabatically from A to B. The solidus (which is also the liquidus in a one-component system) is intersected at pressure

, temperature T

(point B). At B the system becomes univariant and adiabatic upwelling is constrained to the

melting curve BC. Melt fraction increases from B to C, as sensible heat is converted to latent heat. Melting is complete

at C, and melt rises adiabatically from C to D.

We seek an equation that allows us to calculate the extent of melting as a function of

pressure along the two-phase segment of the adiabat. We will initially restrict our discussion

to the simple one-component system depicted in Fig. 10.8, because this problem has a simple

analytical solution that will allow us to examine the fundamental thermodynamic aspects

of decompression melting. Later we will see how the results generalize to multicomponent

systems in which there is a finite temperature difference between solidus and liquidus.

If decompression melting occurs during isentropic upwelling then we can begin with

equation (4.140) and modify it so as to include the thermal effect of the phase transition.

We write the new equation on a molar basis, as follows:

dS =



∂S

∂T



dT +



∂S

∂P



dP +



∂S

∂ϕ



P ,T

dϕ =0, (10.24)

where ϕ is (molar) melt fraction, i.e. ϕ =1 corresponds to melting of one mol of substance.

Clearly, (∂S/∂ϕ)

P ,T

is the molar entropy of fusion, 

S,so(10.24) becomes (see also

(4.141)):

dT −αV dP +

Sdϕ = 0. (10.25)

499 10.6 Decompression melting

Let the Clapeyron slope of the melting reaction be y =(dP/dT )

melting

. The temperature at

any point along the two-phase segment, BC in Fig. 10.8, is then given by:

T = T

P −P

. (10.26)

Taking the derivative of (10.26), substituting in (10.25), rearranging and simplifying

we get:

dϕ

=−



(

+P −P

)

αV



. (10.27)

The material properties C

,V and α correspond to the two-phase system and must there-

fore vary between those of the pure solid at B to those of the pure melt at C. Including

weighing functions such as C

= C

(ϕ), etc., is certainly possible but it complicates the

equation tremendously, requires a numerical solution, and obscures the physics contained

in 10.27. For simplicity we will use values for C

,V and α that are intermediate between

characteristic solid and melt values for upper mantle phases. Reasonable estimates are:

≈ 200 J K

−1

mol

−1

, α ≈ 6 ×10

−5

−1

and V ≈4.7 J bar

−1

mol

−1

. The other param-

eters in equation (10.27) are independent of ϕ. We can choose typical values of 56 J K

−1

mol

−1

for the entropy of melting, and 80 bar K

−1

and 1600 K for the Clapeyron slope and

initial melting temperature in the upper mantle, respectively.

Equation (10.27) applies to any point along the two-phase segment of the adiabat: {T

}

could be the point where the solidus is first intersected, or it could be any other point between

B and C. Let us consider first a situation in which {T

} is some arbitrary point in the

two-phase segment of the adiabat, and P is infinitesimally close to P

, so that P

−P ≈ 0

and T ≈ T

. We can then simplify (10.27) as follows:

dϕ

≈−

yT 

αV



, (10.28)

and in this form it is easier to dissect the physics of decompression melting. Note first that

decompression melting means that dϕ/dP < 0. Because all of the variables on the right-hand

side of (10.28) are positive quantities, it follows that the first term contributes to melting,

whereas the second one opposes melting. The reason is obvious: the first term represents

conversion of sensible heat to latent heat (it contains the ratio C

/

H ) whereas the

second term represents the amount of thermal energy that is converted to expansion work.

The melting rate is controlled by the difference between the Clapeyron slope of the melting

reaction and the slope of the isentrope. This can be seen graphically in Fig. 10.8: the energy

available for melting is a function of the horizontal distance between the adiabat and the

melting curve. The faster the divergence rate between the two curves, the greater the melting

rate will be. Using the values for the upper mantle that we chose in the previous paragraph

we get:

−

yT 

≈−0.028 kbar

−1

αV



≈0.005 kbar

−1

. (10.29)

In this case the energy that goes into expansion work is about half an order of magnitude

smaller than the energy used in melting. The resulting melting rate, dϕ/dP ≈−0.023 kbar

−1

is quite low. Assuming that the melting rate stayed constant (which it doesn’t because

(10.28) is a linear approximation to (10.27)) complete melting would require ∼50 kbar of

500 Melting in planetary bodies

decompression. Compare this value to our estimate in Fig. 10.7 that melting under Earth’s

mid-ocean ridges begins at a pressure of ∼17 kbar.

Equation (10.28) shows that the rate of decompression melting increases with decreasing

melting temperature. As we saw in Section 10.1.1, melting is a discontinuous loss of long

range order. Because the lattice disorder term is not a strong function of temperature, entropy

of melting can be expected to stay more or less constant with temperature (equation (10.6)).

Entropy of melting may vary with pressure, but again we can expect such variations to

be small, as they would arise from differences in the compressibilities of solid and melt

(equation (10.6)). Experimental measurements generally confirm these expectations (e.g.

Kojitani & Akaogi, 1997). If the entropy of melting stays constant then the enthalpy of

melting must increase with temperature, and the melt productivity must concomitantly

decrease. This has the somewhat counterintuitive consequence that decompression melting

along an adiabat with a higher potential temperature (e.g. at mantle hot spots) requires

a greater amount of decompression to produce the same amount of melt that would be

produced along a colder adiabat (e.g. at mid-ocean ridges), although melting would begin

deeper along the hotter adiabat (Fig. 10.7).

In order to calculate the total amount of melt produced by a given amount of decompres-

sion we integrate equation (10.27) between ϕ =0atP =P

and any other value of P ≥P

Ignoring changes in C

,V and α with ϕ we get:

ϕ =−





+P −P



αV



(

P −P

)

. (10.30)

Note that ϕ only depends on the amount of decompression, not on the absolute value

of P

, although of course T

changes with P

. Defining the pressure interval over

which decompression melting takes place as P = P − P

, we can re-write (10.30)as

follows:

ϕ =−





1 +

P



αV



P . (10.31)

This equation overestimates actual melt production for two reasons. In the first place, (10.31)

describes melting of a one-component system, in which the solidus and the liquidus coin-

cide. In reality the mantle is a multicomponent system in which the temperature interval

between solidus and liquidus is of the order of several hundred degrees. In order for melt-

ing to continue above the solidus temperature must increase relative to the value given by

equation (10.26), so that less “sensible heat” is available for conversion to enthalpy of melt-

ing. We will estimate the magnitude of this effect in Section 10.6.4. Second, equation (10.31)

assumes batch melting, i.e. that melt and solid remain at equilibrium throughout the melting

process. If melt is extracted as it is produced then the system is no longer adiabatic. The

system in this case loses heat (and thus entropy), and melt productivity must decrease. We

prove this formally next.

10.6.3 Fractional decompression melting of a one-component system

Batch melting, in which the melt remains in equilibrium with the solid until a desired melt

fraction is attained, or until melting is complete, is one end-member of a spectrum that

extends, at the other end, to fractional melting. During fractional melting melt is removed

at the same rate as it is produced, so effectively at any given moment there is only an

501 10.6 Decompression melting

infinitesimal amount of melt in equilibrium with the solid. The process is not adiabatic,

but it can be broken down into an infinite number of steps, each of which is adiabatic and

isentropic. Equation (10.27) applies to each step: an infinitesimal amount of melt is produced

isentropically, then removed, a new melt increment is produced, and so on. The equation

needs to be modified, however, to account for the fact that the mass of rock that undergoes

partial melting decreases continuously. Each melt increment in equation (10.27) will now

be measured relative to the amount of solid that remains. Call this melt infinitesimal dϕ

We then re-write equation (10.27) as follows:

dϕ

=−



(

+P −P

)

αV



(10.32)

with the understanding that (10.32) applies to each infinitesimal isentropic melting step. If

the total amount of melt generated and extracted from one (initial) mol of solid is ϕ, then

a small incremental amount of melt of δϕ mols corresponds to a per mol increment in melt

fraction, δϕ

(i.e. measured relative to the remaining solid) of:

δϕ

1 −ϕ

(10.33)

so, passing to the limit:

dϕ

=1 −ϕ. (10.34)

From (10.32) and (10.34), using the chain rule:

dϕ

(

1 −ϕ

)



−



(

+P −P

)

αV





, (10.35)

which we integrate by rearranging as follows:

dϕ

(

1 −ϕ

)



−



(

+P −P

)

αV





dP . (10.36)

The integral of the right-hand-side term is identical to (10.30), so, after rearranging:

ϕ = 1 −exp







1 +

P



−

αV



P



. (10.37)

Melt production by fractional decompression melting of a one-component system

(equation (10.37)) is compared to batch melting (equation (10.30)) in Fig. 10.9. Material

properties and other physical parameters are the same as those used in equations (10.29).

As we expected, fractional melting generates less melt than batch melting, because migra-

tory coconuts err.... melts extract thermal energy from the system. The two curves diverge

strongly for large values of P . Since the enthalpy of fusion comes exclusively from cool-

ing, the system can never become completely molten if it loses melt at the same rate as

it is produced, so the fractional melting curve approaches ϕ = 1 asymptotically. The two

curves, for batch and fractional melting, bound a region of possible decompression melting

behaviors. Melting in nature is likely to proceed in some intermediate fashion. One pos-

sibility is that melt is extracted continuously once some finite melt fraction is attained –

this differs from fractional melting in that a finite, as opposed to infinitesimal, amount of

502 Melting in planetary bodies

–10

–80–60–40–20

0.2

0.4

0.6

0.8

∆P (kbar)

Decompression melting of a one-component system

Batch melting

Fractional melting

Fig. 10.9

Variation in melt fraction during batch and fractional decompression-melting of a one-component system. Batch

melting is assumed to be isentropic. During fractional melting melt leaves the system at the same rate as it is

produced, carrying thermal energy, and entropy, with it.

melt is always present. Another possibility is that melt is generated in small batches that are

extracted discontinuously. Whatever the actual melting mechanism, however, melt produc-

tivity by decompression melting of a one-component system is bound by two curves such

as in Fig. 10.9.

10.6.4 Decompression melting in multicomponent systems

Melting of rocks takes place over multivariant intervals, extending from the solidus to

the liquidus. A rather simplistic view of this process is presented in Fig. 10.10.Asinthe

one-component case (Fig. 10.8) melting begins at point B, at temperature T

and pressure

, where the adiabat with potential temperature T

intersects the solidus. The melt +

solid assemblage is in this case multivariant, so temperature increases above the solidus as

melting progresses. Adiabatic upwelling therefore causes the P –T conditions of the system

undergoing melting to describe a path such as BC in the figure. The liquidus is intersected

at point C, and further upwelling occurs along the adiabat with potential temperature T

p, m

Compared to the one-component system (Fig. 10.8), in this case there is less thermal energy

available for melting, because some enthalpy must be used to raise the temperature above

the solidus. We seek to estimate the magnitude of this effect.

For simplicity we will assume that the solidus and the liquidus are parallel, and that melt

fraction varies linearly between 0 at the solidus and 1 at the liquidus. As it turns out, this

by itself is not a bad assumption for melting of peridotite, but it masks another effect that is

503 10.6 Decompression melting

Temperature

Pressure

solid

melt

solidus

liquidus

p,m

mantle adiabat

melt adiabat

solid + melt

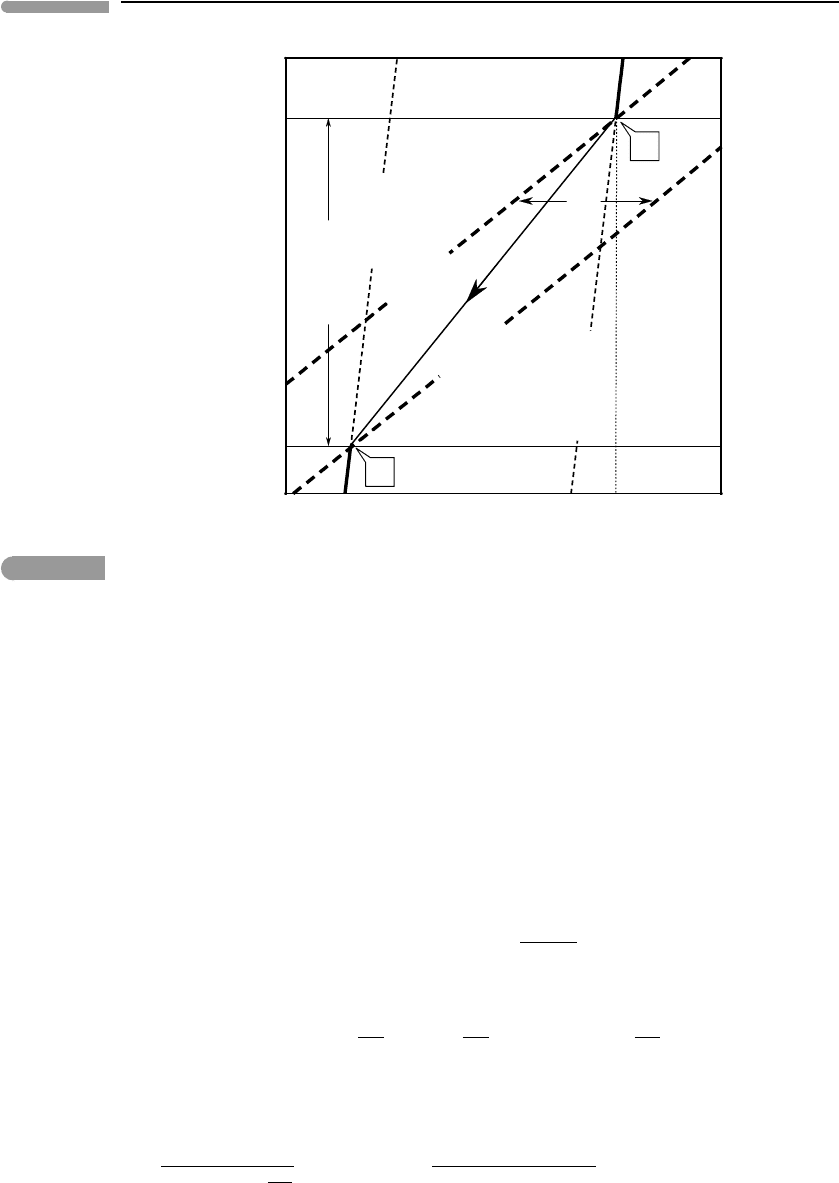
Fig. 10.10

Decompression melting of a multi-component system (compare Fig. 10.8). Melting begins at B, as in the

one-component system, but now in order for additional melting to take place the temperature must increase above

the solidus, as shown by the arrow. The temperature interval between solidus and liquidus, T

, is assumed to be

independent of pressure. In reality the gap between peridotite solidus and liquidus narrows with increasing pressure.

important, and that we will completely ignore. This is the fact that the nature of the melting

reaction changes from the solidus to the liquidus, and also with pressure. We are ignoring

differences in the enthalpy of melting of the various reactions, as well as the enthalpies

of possible reactions among solid phases. The only way of including these effects is by

means of a sophisticated thermodynamic model for silicate melts such as pMELTS, which

is beyond the scope of this book.

Let T

be the constant temperature difference between solidus and liquidus. Ignoring all

compositional effects, and assuming a linear increase in melt fraction over the temperature

interval T

, we write the equation for the BC melting curve in Fig. 10.10 as follows:

T = ϕT

P −P

. (10.38)

The total differential of T is:

dT =



∂T

∂ϕ



dϕ +



∂T

∂P



dP = T

dϕ +

. (10.39)

Substituting (10.38) and (10.39)in(10.28), making P = P − P

, and rearranging we

obtain the following expression for batch melting:



ϕT

P

+



dϕ +



(

ϕT

)

+P

−αV



(

P

)

=0 (10.40)

504 Melting in planetary bodies

and similarly for fractional melting, using (10.36):



ϕT

P

+



dϕ

1 −ϕ



(

ϕT

)

+P

−αV



(

P

)

=0. (10.41)

These equations cannot be integrated analytically, but generating numerical approximations

is a simple exercise with Maple (Software Box 10.1).

Software Box 10.1 Calculation of decompression melting

The Maple worksheet decompression_melting.mw contains two procedures,

batch_melting and fractional_melting, that use Maple’s fsolve to solve

equations (10.40) and (10.41), respectively. The two procedures are identical except for

the core equation.

When invoking the procedure one specifies the temperature and pressure at which

the adiabat first intersects the solidus (in Centigrade and kbar) and a filename for Maple

to send the output to. All other model parameters can be changed by editing the proce-

dure. This includes: the Clapeyron slope of the solidus, the solidus–liquidus temperature

interval, heat capacity, entropy of melting, coefficient of thermal expansion, molar vol-

ume, and the pressure increment for the solution. The latter must be a negative number

(decompression) and must be expressed in bar.

The procedure generates a text file in which each line corresponds to a decompression

step, extending from the initial intersection of the solidus with the adiabat to the planet’s

surface. The first field in each line is the total amount of decompression (in kbar), the

second field is melt fraction, the third field is temperature (in Centigrade), and the fourth

field is pressure (in kbar).

Worked Example 10.1 Decompression melting in the Earth’s mantle

We apply numerical solutions of equations (10.40) and (10.41) to study decompression

melting of the Earth’s upper mantle under different thermal regimes. We start with a model

dry peridotite solidus, simplified after McKenzie and Bickle (1988) for P<45 kbar, and

Herzberg et al. (2000) at higher pressure, as shown in Figs. 10.11 and 10.12. A characteristic

value of T

for mantle peridotites is ∼500 K. We therefore draw the peridotite liquidus

parallel to the solidus and displaced 500 K towards higher temperature. We study decom-

pression melting along three possible mantle adiabats, with potential temperatures of 1300,

1500 and 1700

◦

C. The first two may represent conditions under present-day terrestrial mid-

ocean ridges and oceanic islands, respectively. The last one represents possible conditions

in the Archaean Earth. The three adiabats intersect the peridotite solidus at temperatures of

approximately 1600, 1820 and 2050 K, and pressures of 16, 34 and 57 kbar, respectively.

We use the same material properties and other physical parameters as in previous exam-

ples (e.g. equations (10.29)), except that we make the Clapeyron slope y =80 bar K

−1

for

melting at mid-ocean ridges and oceanic islands, and 85 bar K

−1

along the hotter adiabat,

to reflect the fact that the peridotite solidus steepens with increasing pressure (we discuss

this in more detail in the next example).

505 10.6 Decompression melting

1000 1200 1400 1600 1800

Temperature (°C)

Pressure (kbar)

–6

–50 –40

–30

–20 –10 0

0. 1

0. 2

0. 3

0. 4

0. 5

Decompression (kbar)

Melt fraction

= 1300

= 1500

= 1700

solidus

liquidus

R O M

t a b a i d a

I O

t a b a i d a

n a e a h c r A

t a b a i d a

MORB

OIB

Archaean komatiites

Batch melting

Fig.10.11Simpliﬁedmodelforbatchmeltingoftheterrestrialmantle.SolidusafterMcKenzieandBickle(1988)for

P<45kbar,andHerzbergetal.(2000)athigherpressure.Theliquidusdrawnparalleltothesoliduswith

=500 K. Three mantle adiabats are shown, with potential temperatures of 1300, 1500 and 1700

◦

C. Solid lines

with arrows show melting paths, corresponding to the segment BC in Fig. 10.10. The broken arrow forking from the

hottest adiabat shows adiabatic ascent of melt with eruption temperature of 1400

◦

C. The bottom diagram shows

melt fraction as a function of decompression. A range is shown for the hottest adiabat (“Archaean komatiites”), bound

between the decompressive path that generates melt with 1400

◦

C eruption temperature and the maximum possible

decompressive path (to P =0).

506 Melting in planetary bodies

1000 1200 1400 1600 1800

Temperature (°C)

–60 –50 –40 –30 –20 –10 0

0. 1

0. 2

0. 3

0. 4

Decompression (kbar)

Melt fraction

Pressure (kbar)

= 1300

= 1500

= 1700

solidus

liquidus

R O M

t a b a i d a

I O

t a b a i d a

n a e a h c r A

t a b a i d a

MORB

OIB

Archaean komatiites

Fractional melting

Fig. 10.12 Same as Fig. 10.11, but for fractional melting.

The solid arrows in Figs. 10.11 and 10.12 are isentropic melting paths, corresponding to

BC in Fig. 10.10. The P –T paths are calculated by first solving equations (10.40)or(10.41)

for ϕ as a function of P , and then substituting these values of ϕ in equation (10.38). In every

case the decompression melting paths intersect the surface before reaching the liquidus. The

batch melting paths reach the surface at temperatures of ∼1200

◦

C and ∼1300

◦

C for mid-

ocean ridges and oceanic islands, respectively. The corresponding temperatures assuming

fractional melting are ∼10–20

◦

C lower. If mantle upwelling caused decompression melting

to continue to the surface erupted magmas would have these temperatures. Eruption

507 10.6 Decompression melting

temperatures would be higher if melts separated from their source regions at depth. The

agreement with observed basalt eruption temperatures is quite good, but this should be

hardly surprising, as the potential temperature of the mantle is to a large extent constrained

from basalt eruption temperatures.

Calculated melt fractions along the isentropic melting paths are shown in the bot-

tom panels of the figures. Maximum melt production at mid-ocean ridges, assuming

that the upwelling mantle melts continuously from 17 kbar (where the solidus is inter-

sected) to zero pressure, ranges from 17%–19%, depending on whether one assumes

fractional or batch melting, respectively. This happens to be a reasonably good esti-

mate. The corresponding values for melting under oceanic islands are 30%–36%, for a

maximum decompression interval of 35 kbar. These values possibly overestimate actual

melt fractions to some extent, although the generally more mafic nature of ocean island

basalts compared to MORBS is consistent with them representing a higher melt fraction of

peridotite.

Melting of the mantle along our hypothetical Archaean adiabat, from the solidus at

57 kbar to the surface, would generate 44%–54% melt with eruption temperatures of

1300–1350

◦

C. Komatiite eruption temperatures appear to have been somewhat higher than

this, perhaps ∼1400

◦

C. Melts with this eruption temperature could have been extracted

from the upwelling mantle region at pressures of 7–14 kbar, for batch and fractional melt-

ing, as shown by the broken arrows in the figures. The more restricted decompression

melting intervals would generate between 32% and 44% melt, which is not altogether

unreasonable for komatiites. The geometry of the figure shows that an adiabat with a

potential temperature higher than 1700

◦

C would intersect the solidus deeper and the

resulting melting path would reach the 1400

◦

C melt adiabat at a shallower depth than

the one emanating from the 1700

◦

C adiabat. Thus, it would generate a higher frac-

tion of melt with the same eruption temperature. No surprise here – it is simply energy

conservation.

Worked Example 10.2 Melting in the Martian mantle

We can use equations (10.40) and (10.41) to assess the plausibility of the Martian mantle

models that we developed in Chapter 3. In Section 3.9 we saw that two possible models for

the Martian interior are a relatively thin lithosphere (∼250 km thick) capping a hot mantle,

or a thick lithosphere (∼700 km) overlying a colder mantle, but still hotter than the Earth’s.

Let us assume that the mantle potential temperatures for the two models are 1800

◦

C and

1500

◦

C, respectively, which are approximately 500

◦

C and 200

◦

C hotter than the terrestrial

mantle under mid-ocean ridges. Intersection of these adiabats with the model peridotite

solidus (shown in Fig. 10.11) occurs at temperatures of 1543

◦

C and 1935

◦

C, and pressures

of ∼34 and 105 kbar, respectively. We assume that this solidus curve is applicable to the

Martian mantle, which is not strictly true but there are larger sources of uncertainty. The

Clapeyron slope of the solidus steepens sharply with pressure above about 60 kbar. The

adiabat also steepens, although to a lesser extent. Equations (10.40) and (10.41) assume

that both of these quantities are constant, and although it is possible to modify them to

account for their pressure dependency this complicates the equations considerably and is

left as an exercise for the reader. As we saw, the degree of melting is ultimately determined

by the difference between the slope of the isentrope and that of the melting reaction, and this

difference varies less strongly with pressure than the Clapeyron slope of the solidus.