Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

488 Melting in planetary bodies

0 5 10 15 2

1800

1900

2000

2100

2200

M=m

Melting temperature (K)

z,m

= 10 wt%

z,m

= 1 wt%

Melting point depression of forsterite

Fig. 10.3

Melting temperature of forsterite as a function of the parameter M =ratio of molecular weight forsterite, m

,to

molecular weight of “impurity” component in the melt, m

. The concentration of impurity in the melt is constant

along each curve, at 1 and 10 wt%.

Defining the ratio of molecular weight of major component to molecular weight of impurity

M =m

, we get:

z,m

(

M −1

)

z,m

+100

(10.19)

and:

T ≈ T



1 −

z,m

(

M −1

)

z,m

+100





. (10.20)

We see that the molecular weight of the impurity relative to that of the major component

has a large effect on the magnitude of the melting point depression, simply because a given

mass of impurity represents a greater number of mols the lower its molecular weight is

relative to that of the host. This is shown by the curves of T vs. M in Fig. 10.3. The curves

are calculated with equation (10.20) for values of T

= 2174 K and 

S = 56 J mol

−1

, which correspond to melting of forsterite at 1 bar, and constant values of C

z,m

of 1

and 10 wt%.

10.4.2 Effect of partitioning of incompatible trace components on melt generation

In Section 10.3 I was somewhat careless about the thermodynamics of melting. It is now

necessary to clean up the act. Naively, one could think that the “progressive melting” that

489 10.4 The effect of “impurities”

I referred to in Section 10.3 corresponds to melting at constant temperature, as a result

of slow addition of heat (enthalpy of melting). This is not the case, however. Consider an

idealized system in which forsterite is pure Mg

SiO

. Melting in this system is univariant.At

constant pressure there is a unique temperature at which crystal and melt are at equilibrium,

i.e. the solidus and liquidus temperatures are the same. Suppose now that olivine contains

a trace component dissolved in its crystalline structure. This could be a cation substituting

for Mg, or it could be a molecular species, such as H

O or some other volatile component,

accommodated interstitially in its crystalline structure. In any case, we are now dealing

with a two-component system, and since the extra component does not cause a new phase

to form, the melting reaction becomes divariant: solidus and liquidus temperatures do not

coincide, nor will they in general be the same as the melting temperature of pure forsterite.

Whether this thermodynamically inevitable effect of incorporation of trace components is

petrologically significant is another question, to which we now seek answers. This topic

has been explored in detail by Hirschmann and collaborators in a number of recent and

clear contributions (Hirschmann, 2006; Hirschmann et al., 2009; Tenner et al., 2009). Here

I will derive a set of very general equations applicable to simple systems of what I shall

call “one component plus a trace”. By this I mean that the system is binary when the

trace component is included, and that we will compare its behavior to that of the unitary

trace-free system.

We seek an equation for the solidus temperature of a crystal that contains a trace

component dissolved in it. From (10.15) and (10.19) we write:

z,m

z,i

(

M −1

)

z,i

+100D

s/m

(

1 −ϕ

)

+ϕ

. (10.21)

Substituting this expression in (10.17) and setting ϕ =0 yields the desired equation for the

solidus temperature, T



1 −

z,i

(

M −1

)

z,i

+100D

s/m





. (10.22)

This equation allows us to explore the effects of the three parameters, M, D

s/m

and C

z,i

on the melting point of a crystal. Figure 10.4 shows curves of T

vs. C

z,i

calculated for

melting of forsterite at 1 bar (T

= 2174 K, 

S = 56 J mol

−1

, same as Fig. 10.3).

The horizontal axis extends to a maximum value of 0.1 wt% (=1000 ppm), which makes

it clear that even trace amounts of “impurities” can have a dramatic effect on the solidus

temperature of a crystal (emphasis important, as we shall soon see). The values of the

partition coefficient and of the molecular weight of the trace component relative to that of

the host both have major effects on the magnitude of the melting point depression. The more

incompatible a component is, the more it partitions into the melt and therefore the greater

the melting point depression is. We discussed the effect of molecular weight in Section

10.4.1, but let us now consider specific examples.

10.4.3 Volatiles and melting

Volatiles, and in particular H

O, have a strong effect on the melting point of silicate systems.

The key to this behavior is, to a considerable extent, the low molecular weight of volatile

species. What determines the maximum magnitude of the melting point depression is the

solubility of the volatile in the silicate melt at the conditions of interest, i.e. how large C

z,m

490 Melting in planetary bodies

0 0.02 0.04 0.06 0.08 0.1

1800

1900

2000

2100

z,i

(wt%)

Melting temperature (K)

Melting point depression of forsterite

M=10

s/m

= 0.005

M=10

s/m

= 0.01

M=1

s/m

= 0.005

M=1

s/m

= 0.01

Fig. 10.4

Melting temperature of forsterite as a function of bulk initial concentration of impurity, for different values of the

parameter M, and different solid–melt partition coefﬁcients, D

s/m

can get. But for a given mass solubility, the lower the molecular weight of the volatile,

the stronger its effect on the melting point will be. Volatile solubility in silicate melts is a

complicated function of volatile and melt compositions, pressure and temperature. A vast

literature on this topic exists, of which a reasonably recent summary can be found in Volume

30 of Reviews in Mineralogy. Volatile solubilities in silicate melts increase with pressure at

constant temperature. If any generalizations beyond this one are possible, one could say that:

(i) H

O solubility in silicate melts is significant (in the wt% level) beginning at pressures

of a few hundred bars, (ii) CO

solubility reaches wt% levels only at pressures of order

10 kbar, (iii) fluorine solubility may be comparable to that of H

O, whereas chlorine may

be at least one order of magnitude less soluble, (iv) sulfur solubility is strongly dependent

on oxygen fugacity and the oxidation state of iron, and (v) nitrogen solubility may become

quite large only at lower mantle pressures.

Another important consideration is the nature of the sub-solidus host for the volatile

species. One possibility (see Worked Example 6.3) is that a volatile phase exists at equilib-

rium with the rock. If the volatile phase is pure (say, pure H

O), then the melt is saturated in

the volatile species. In this case X

z,m

takes its maximum value at the given P and T , and the

solidus temperature takes its minimum value (equation (10.17)). A variation on this theme,

that we discuss in Section 10.7, is a situation in which the volatile phase percolates through

the rock but the volatile mass flux is low enough that the melt does not become saturated

in volatiles, at least initially. Another possibility is that the volatile species is an essential

structural component of one or more of the mineral phases in the rock, for example, micas,

491 10.4 The effect of “impurities”

amphiboles, apatite or carbonates. In this case it does not become available until the host

crystalline phase breaks down. This is dehydration melting (discussed in Worked Exam-

ple 6.3). Chemography requires that in this case the concentration of the volatile in the melt

be lower than the saturation concentration. The dehydration-melting solidus temperature

must therefore be higher than the vapor-saturated solidus (equation (10.17), Fig. 6.9). Yet

another possibility, that may be important in planetary mantles, is that the volatile species

is present as a trace component in a nominally anhydrous mineral.

10.4.4 Melting point depression by trace volatiles

Olivine at upper mantle pressures can dissolve a few hundred ppm of H

O, and measured

values of D

olivine/melt

for H

O are in the range 0.006 to 0.009; see, for example, Hirschmann

(2006); Hirschmann et al. (2005); Tenner et al. (2009). As pointed out by these authors, a

reliable estimate of the melting point depression is complicated by the fact that the speciation

of H

O in silicate melts is far from being completely understood. We can postulate, however,

that the molecular weight of H

O species is likely to be much lower than that of silicate

species, so perhaps the curves for M = 10 in Fig. 10.4 yield a reasonable estimate of the

effect of H

O on the melting point of forsterite. If this is the case then a few hundred ppm

of H

O dissolved in forsterite will lower its solidus temperature by as much as 150–200 K,

which may be significant when considering magma generation in planetary mantles (see

Section 10.6). Suppose, on the other hand, that forsterite contains the same mass of a trace

incompatible cation in solution, for example potassium. We can reasonably assume that

when K enters the melt it does so as a silicate species, so in this case M may be closer to 1.

For a partition coefficient similar to that of H

O the melting point depression would be only

∼20 K. These estimates ignore the effect of any excess chemical potential of the major melt

component (i.e. γ

r, m

in equation (10.17)). A value of this factor greater than 1 would raise

the solidus temperatures relative to those in Fig. 10.4, but the behavior depicted in Figure

10.4 is nonetheless qualitatively correct.

These results correspond to generation of an infinitesimal amount of melt at the solidus.

A different question is that of how much melt forms as a function of temperature above the

solidus. For a strongly incompatible component we expect that, as melt fraction increases

above the solidus,the concentration of the trace component in the melt will initially drop very

rapidly (Fig. 10.2), giving rise to a negative feedback effect that will limit melt generation.

We can examine this by substituting (10.21)in(10.17) and solving for the melt fraction, ϕ.

After some uninspiring algebra:

ϕ =

1 −D

s/m







z,i

100







1 −







−M +1







−D

s/m







. (10.23)

Note that this equation blows up for T = T

, as it must, for the liquidus (ϕ = 1) must

also be attained at a temperature lower than the melting point of the pure system (T

The liquidus temperature can be calculated by substituting (10.21)in(10.17) and setting

ϕ =1. It is (obviously) independent of D and for all likely values of C

z,i

and M it is only a

fraction of a degree to a couple of degrees lower than the melting point of the pure system.

Equation (10.23) is plotted in Fig. 10.5, for a constant value of C

z,i

= 0.05 (= 500 ppm).

The plot confirms our suspicion that, even if a strongly incompatible trace component with

a low molecular weight can cause a strong depression of the solidus, the increase in melt

492 Melting in planetary bodies

1950 2000 2050 2100 2150

0.02

0.04

0.06

0.08

0.1

Temperature (K)

Melt fraction

Melting point depression of forsterite

z,i

= 500 ppm

M=10

s,m

= 0.005

M=10

s,m

= 0.01

M=1

s,m

= 0.005

M=1

s,m

= 0.01

Fig. 10.5

Forsterite melt fraction as a function of temperature, for different values of the parameter M and different solid–melt

partition coefﬁcients, D

s/m

. The bulk initial concentration of impurity is 500 ppm in all cases.

fraction above the solidus is painfully slow, requiring perhaps 100 K to generate 1% melt.

The rate of melting for a system in which the impurity is closer in molecular weight to the

major component is greater, but the melting point depression is relatively minor to begin

with. There is no free lunch.

The principles summarized in Figs. 10.4 and 10.5 apply to multicomponent systems, such

as rocks, but there is a potentially important difference with the one-component system,

which is shown schematically in Fig. 10.6. In this figure I use the labels “dry” solidus

and “dry” liquidus to refer to the solidus and liquidus of the system in the absence of a

trace component. As we saw, the latter could be a volatile species, but it could also be

an incompatible trace element, such as an alkali in a magnesium silicate. Regardless of

the number of components in the system, addition of a trace component lowers both the

solidus and the liquidus temperatures. Depression of the solidus can be drastic, depending

on the nature of the impurity, its abundance, and its partition coefficient. Depression of the

liquidus, in contrast, is always vanishingly small, as for ϕ =1 the concentration of the trace

in the melt is always small. The initial rate of increase of melt fraction may be very slow

(see also Fig. 10.5) but, if the solidus depression is large enough, the melt fraction at the

temperature of the dry solidus of a multicomponent system may be substantial. One way of

looking at this is that the importance of trace amounts of volatiles in nominally anhydrous

mantle phases is not so much that they lower the solidus temperature as the fact that they

raise the amount of melt produced at temperatures near that of the dry solidus. Quantifying

these effects, however, requires a detailed thermodynamic model of multicomponent silicate

melts, which is beyond the scope of this book (see, for example, Hirschmann et al., 1998,

1999a,b).

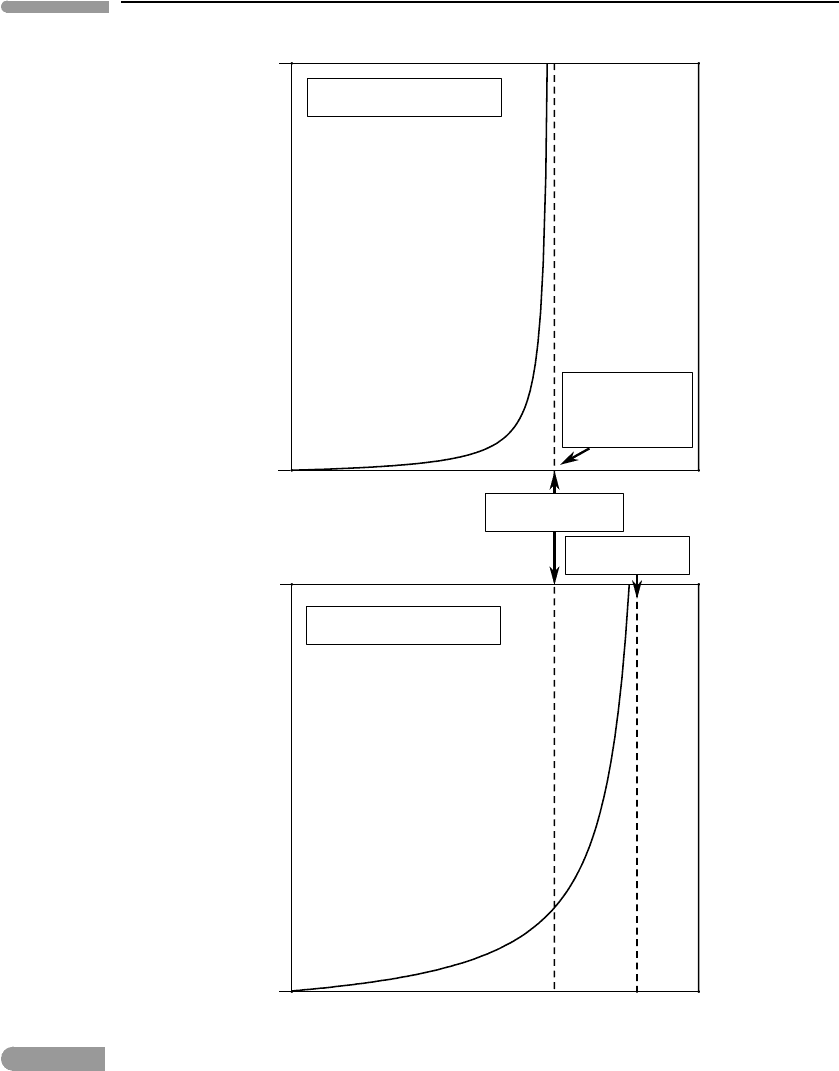
493 10.4 The effect of “impurities”

"Dry" solidus

"Dry" liquidus

One component system

Multicomponent system

"Dry" liquidus

"Dry" solidus

Fig. 10.6

Schematic diagrams comparing variation in melt fraction with temperature in one-component and multicomponent

systems. Bulk initial concentration of impurity and all other parameters are the same in both diagrams. Liquidus

depression is negligible in both cases.

494 Melting in planetary bodies

10.5 Melting in planetary interiors

In Chapter 2 we discussed the sources of thermal energy in planetary interiors. With the

exception of catastrophic events, such as planetary-sized impacts, core formation, tidal

de-spinning and perhaps decay of abundant short-lived isotopes, all of which may have

been common in the early Solar System, the rate of heating of planetary interiors is not

sufficient to cause wholesale melting. Formation of magmas is always localized and entails

less than complete melting of the parent solid assemblage. We seek to understand what

causes localized partial melting in planetary interiors.

The ratio H

fusion

for silicate minerals is of order 10

–10

K. Melting a given

amount of rock requires the same amount of energy as raising its temperature by hundreds

of degrees. This is a key part of the explanation for why magmas typically do not carry

significant superheat, or in other words, that eruption temperatures are not normally above

liquidus temperatures. It also tells us that melting must have a considerable effect on a

planet’s thermal gradient. Let us define our thermodynamic system as a region of the inte-

rior of a planetary body in which partial melting takes place. Focusing on its fundamental

thermodynamic aspects we can consider three simple end-member situations. First, melt-

ing may take place in an open system, in which there is mass and heat transfer across its

boundaries. This typically involves influx of a volatile phase that lowers the melting point

of the solid assemblage (Section 10.4.4). Melting above terrestrial subduction zones may

largely occur in this way. Second, melting may occur in a closed but non-adiabatic system,

i.e. one that can exchange heat but not matter with its environment. This may be a magma

generation process at major planetary-scale compositional discontinuities, at which jumps

in density, melting point and rheological properties may allow the juxtaposition of advec-

tive and diffusive heat-transfer regimes. Partial melting of the Earth’s continental crust

by ponding of mafic magmas near the Moho may be an example. The problem with this

mechanism is that it relies on diffusive heat transfer into the region that undergoes melting,

and the very long time scales for heat diffusion may render it inoperable (Chapter 12). One

way of getting around this difficulty is to decrease the diffusive lengthscale which would

be the case, for example, if mafic magmas intrude the crust as a complex of closely spaced

dikes. Finally, melting may occur under adiabatic conditions if the solidus of the mineral

assemblage intersects the adiabatic thermal gradient. This process, called decompression

melting, is likely to be the most widespread magma generation process in convective plan-

etary bodies. It is responsible for magmatism at Earth’s mid-ocean ridges, hot spots and

large igneous provinces, such as continental flood basalts and oceanic plateaus. It is almost

certainly responsible for magmatism in Venus and Mars, and perhaps for Io’s volcanoes as

well. Because of its importance we will discuss this process first.

10.6 Decompression melting

10.6.1 Fundamental relations

In Chapter 3 we derived expressions for the adiabatic temperature gradient, as a function

of either depth (equation (3.35)) or pressure (equation (3.32)). In Chapter 4 we saw that

these equations correspond to a specific type of adiabatic process, during which entropy

495 10.6 Decompression melting

is constant (Worked Example 4.6), and that adiabatic but not-isentropic transformations

are also possible (Section 4.4). We have calculated and used adiabatic thermal gradients in

several discussions without paying much attention to this distinction, which is generally

safe to do in systems in which neither inelastic deformation nor phase separation take place.

We can ask, however, is decompression melting truly adiabatic (see, for example, Asimow,

2002; Stolper & Asimow, 2007)? Of course, if a transformation is not adiabatic it cannot

be isentropic, as heat exchange entails entropy generation, but even if melt generation is

an adiabatic process, is it isentropic? We shall address these questions in a later section,

but the isentropic approximation is an excellent starting point. This is so, first and fore-

most, because the mathematics are simple, allowing us to focus on the physics of melt

generation during mantle upwelling. Second, in many instances decompression melting is

approximately isentropic, at least locally. Third, it is relatively straightforward to start with

the isentropic approximation and add to it the effects of entropy gain or loss arising from

exchange of heat and matter with the environment, or from energy dissipation. Through-

out this discussion, and unless otherwise stated, I will continue to use the terms adiabat,

and adiabatic decompression melting, to mean adiabatic and isentropic, as this is common

throughout the literature. When necessary I will explicitly state whether departures from

the constant entropy assumption need to be taken into consideration.

Using equation (3.35) and the thermodynamic properties of forsterite yields a characteris-

tic adiabatic gradient for the Earth’s upper mantle of ∼0.4 K km

−1

, or, using equation 3.32,

∼1.5 K kbar

−1

. The measured volume and entropy of melting of upper mantle minerals

(forsterite, diopside, enstatite and spinel) yield Clapeyron slopes for their melting reactions

(equation (5.6)) of 50–100 bar K

−1

, or equivalently 10–20 K kbar

−1

. Clearly, the adia-

bat and the melting curve for the mantle can intersect. Whether and where they intersect,

however, and what happens next, depend not only on their relative slopes but also on their

absolute locations.

We will consider melting under Earth’s mid-ocean ridges as our reference model – after

all, this is where most of Earth’s volcanic activity takes place. Let us assume that the

oceanic lithosphere extends to a depth of 150 km, and that the temperature at the base of the

lithosphere is 1650 K (= 1377

◦

C, see Chapter 3). The pressure at that depth is ∼50 kbar

(Chapter 8). From these values and a slope of 1.3 K kbar

−1

we derive the mantle adiabat

shown in Fig. 10.7. The intersection of the mantle adiabat with the Earth’s surface (P =0)

defines the mantle’s potential temperature, which in our example is T

=1312

◦

C. This is

the temperature that the mantle would have if it were allowed to decompress adiabatically

(and, remember, isentropically) to the planet’s surface, i.e. if the lithosphere did not exist

and phase changes did not take place. This may not happen, but knowing the potential

temperature is important because, given that an adiabat is fully determined if we specify a

single {P , T }point on it (Section 3.5), T

allows us to compare the thermal state of different

regions of a convective mantle, as well as the mantles of different planetary bodies. In other

words, comparing how much hotter or colder different parts of a convective region are

requires that we specify the pressure at which we make the comparison, and we choose zero

as the reference pressure.

In Section 3.7.2 we defined the lithosphere as the thermal boundary layer for mantle

convection, meaning that heat transfer across the lithosphere is by diffusion. If we ignore

radioactive heat production (which, if not quite right, is not altogether unacceptable for the

oceanic lithosphere) then the equilibrium lithospheric geotherm is a straight line. In Fig. 10.7

I show this conductive geotherm with a straight line joining the 1650 K temperature at the

base of the lithosphere to a surface temperature of 300 K. This translates to a heat flux of

496 Melting in planetary bodies

1100 1200 1300 1400

T(°C)

P (kbar)

asthenosphere

lithosphere

garnet lherzolite

spinel lherzolite

conductive geotherm

adiabat

model peridotite

solidus

50 bar K

–1

100

bar

–1

basalts

Fig. 10.7

Simpliﬁed thermal conditions in the Earth’s oceanic upper mantle. The thick “dog-leg” line shows the geotherm far

away from a mid-ocean ridge. Under a mid-ocean ridge adiabatic upwelling of the mantle intersects the peridotite

solidus. If the adiabat were able to reach the surface unperturbed its temperature would be the potential

temperature, T

. The difference between T

and basalt eruption temperatures (range shown with an arrow) reﬂects

the enthalpy of melting.

∼50 mW m

−2

, which is a bit on the low side for old ocean floor. Including radioactive

heat production in the lithosphere would probably raise the value to the right ballpark, but

this is not important for the present discussion. What is important is that the geotherm

in an old sector of ocean floor, effectively infinitely removed from any region of active

magma generation, would look like the thick “dog-leg” line in Fig. 10.7, composed of an

adiabatic (advective) segment capped by a diffusive segment. There are places, however,

where advective flow is able to penetrate to depths that are significantly less than that of the

“typical” lithospheric base. This process may be driven either from “above”: the lithosphere

thins in response to stretching, or from “below”: the rate of heat advection is high enough

to thermally “erode” the lithosphere. For our purposes it does not matter which is the case.

What matters is that under those circumstances the adiabatic thermal gradient will extend

to shallower depths, as shown by the line labeled “adiabat” in Fig. 10.7.

The figure also shows the dry model peridotite solidus, after McKenzie and Bickle (1988).

The adiabat and the solidus intersect at a pressure of ∼17 kbar, indicating where decom-

pression melting begins during mantle upwelling. The intersection occurs in the spinel

lherzolite field. This is consistent with the phase equilibrium and geochemistry of MORBs,

suggesting that the processes and thermal conditions summarized in Fig. 10.7 are a feasible

model for melting under Earth’s mid-ocean ridges. The zero-pressure solidus temperature

is 1100

◦

C. Hypothetical solidi going through this temperature and with Clapeyron slopes

497 10.6 Decompression melting

of 50 and 100 bar K

−1

, which bracket the slope range for typical mantle minerals at low

pressure, are also shown. McKenzie and Bickle’s model solidus is almost exactly in the

middle, which may be reassuring at some (subjective) level.

If the enthalpy of fusion of rocks were zero and the melts formed by decompression

melting rose isentropically then they would reach the surface at the mantle’s potential

temperature. This is not the case. Basalt eruption temperatures are typically ∼1200

◦

C. The

difference between this temperature and the mantle’s potential temperature must reflect at

least in part the conversion of sensible heat to latent heat during melting, as first-order phase

transitions are always accompanied by a non-zero enthalpy change. We will discuss this

issue in detail in the next section, but before doing so there are a few more things to learn

from Fig. 10.7.

First, the eruption temperature of a magma formed by adiabatic decompression melting

must be lower than the potential temperature of its mantle source region. Thus, whereas

Fig. 10.7 may be able to account for melting under mid-ocean ridges, it cannot explain

high-Mg basaltic lavas with eruption temperatures in excess of 1300

◦

C, let alone ultramafic

komatiite lava flows. These require mantle potential temperatures significantly higher than

1312

◦

C, which may have been the norm in the Archaean mantle (Worked Example 3.4).

Second, mafic lavas exist that have major and trace element characteristics indicative of

having formed from garnet-bearing peridotites. Figure 10.7 shows that melting in the garnet

lherzolite field can take place through a combination of higher potential temperature, steeper

Clapeyron slope and lower solidus temperature at a given pressure. In view of our discussion

in Section 10.4, the fact that some of these deep magmas tend to be rich in incompatible

elements (e.g. K) and dissolved volatiles may be significant.

10.6.2 Batch decompression melting of a one-component system

We initially consider decompression melting under isentropic conditions. This requires that

the melt remain in the system and in equilibrium with the solid, a process that as we saw

in Section 10.3 is known as batch melting. We will later relax this constraint and allow the

melt to leave the system at the same rate as that at which it is produced. This process, known

as fractional melting, is obviously not adiabatic, and hence not isentropic.

Imagine an idealized planetary mantle composed of a single component (Fig. 10.8). At

pressures greater than P

the temperature is below the solidus and the mantle consists of a

single solid phase, so that it is a divariant thermodynamic system. Upwelling of solid mantle

occurs along an adiabat with potential temperature T

, from A to B in the figure. At point

B the adiabat intersects the solidus at temperature T

and, as a second phase appears, the

system becomes univariant. Adiabatic decompression beyond the intersection point cannot

follow the adiabat calculated with equation (3.32). Rather, it must be constrained to the

solidus (which in this case is also the liquidus), from B to C in Fig. 10.8. It is important

to realize that the two-phase segment of the decompression path, BC, is also adiabatic.

However, it is not described by equation (3.32) because this equation does not take into

consideration the enthalpy of fusion.At point C, when the upwelling mantle reaches pressure

, melting is complete and the system becomes divariant once more. Further ascent, from

C to D, occurs along another adiabat calculated with equation (3.32), but with a different

potential temperature, T

p,m

, and perhaps a different slope arising from differences in material

properties between solid and liquid. The drop in potential temperature from the AB adiabat

to the CD adiabat reflects the enthalpy absorbed by the melting phase transition.