Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

458 Thermodynamics of planetary volatiles

0 0.2 0.4 0.6 0.8 1

X(H

0 0.2 0.4 0.6 0.8 1

X(H

f/f

φ/φ

0.2

0.4

0.6

0.8

2 kbar - 400°C

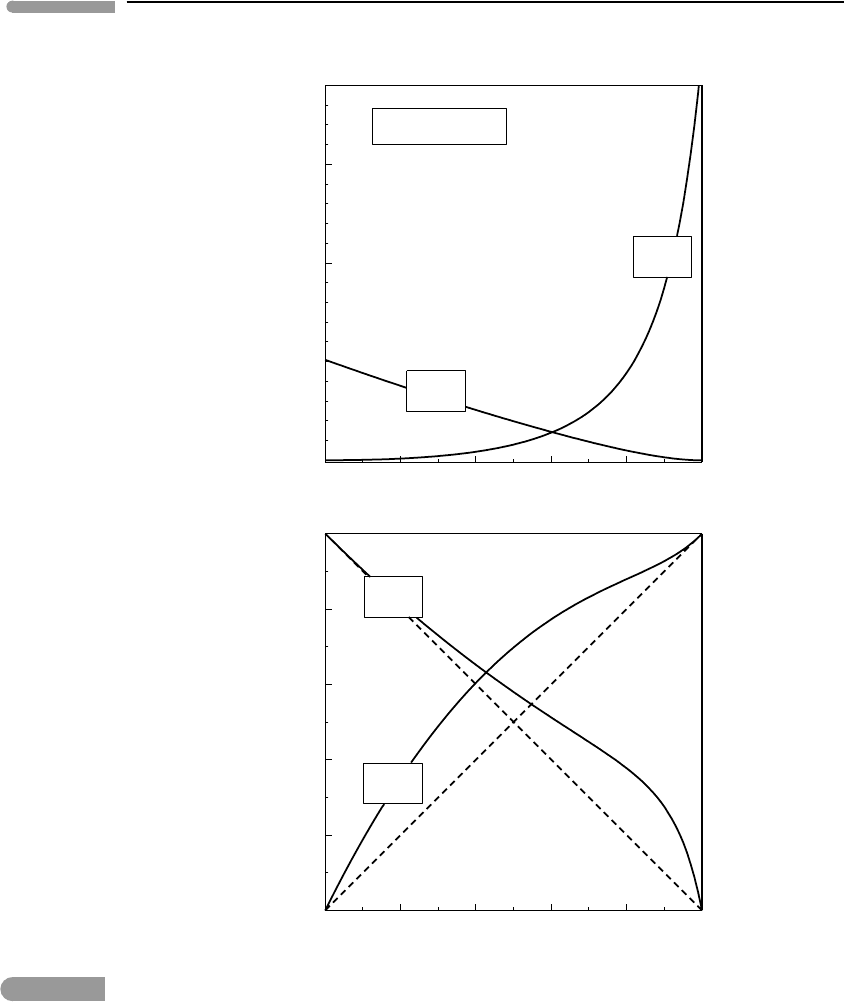
Fig. 9.14 Fugacity coefﬁcients (top) and fugacities (bottom) in a binary H

O–CH

mixture at 2 kbar and 400

◦

C, calculated with

the RK EOS, and normalized to the values of the corresponding standard state functions.

An example of fugacity-composition relationships for a binary fluid, calculated with the

RK EOS (equation (9.80)), is shown in Fig. 9.14. The fluid is assumed to consist of the

species H

O and CH

only, although as we shall see in the following section this may be an

unrealistic constraint. The calculations are done at 2 kbar and 400

◦

C, at which conditions the

RK EOS may still yield reasonably accurate results (e.g. Fig. 9.11). The top panel shows the

ratio of the fugacity coefficient of each species in the mixture to the corresponding standard

459 9.6 Speciation in multicomponent volatile phases

state fugacity coefficient. In a mixture of ideal gases the two curves would be straight lines

at a constant value of 1. The bottom panel shows the ratio of fugacity of each species in

the mixture to its standard state fugacity. This ratio must vanish as the concentration of the

component goes to zero, and approach one as the fluid becomes pure. A mixture of ideal

gases would follow the dashed lines in the figure. The H

O–CH

mixture displays a positive

departure from ideal behavior, which reflects a positive excess Gibbs free energy of mixing

(Section 5.9.1 ). In principle, all of the information describing non-ideal mixing behavior of

real gases is contained in the equation of state and the mixing rules. This of course does not

mean that Fig. 9.14is an accurate representation of an H

O–CH

mixture, first because, as

we shall see in the next section, other species are also likely to be present in non-negligible

amounts in this system, and second because the RK EOS is not accurate above pressures

of a few hundred bars. The latter point becomes particularly serious when dealing with

mixtures of polar and non-polar species, as in this case. Multiparameter equations, such as

the PS EOS, are better suited to the task, but as of this writing they have not been calibrated

for species other than H

O and CO

, thus greatly limiting their usefulness for modeling

many planetary processes.

9.6 Speciation in multicomponent volatile phases

In a multicomponent volatile phase there is virtually unrestricted freedom of formation

of chemical species. Distinct chemical species can be considered to exist in a crystal, but

the type and number of species is limited by the stoichiometry of the compound and the

crystal chemical constraints of the crystalline structure. In a gas there are no such constraints.

Calculating the distribution of species in a homogeneous fluid is important for understanding

its chemical properties (e.g. its oxidizing potential) and physical behavior (e.g. stratification

of fluid composition in a gravitational field).

We will discuss two different approaches to calculating fluid speciation. The chemical

equilibrium approach is based on finding a linearly independent set of homogeneous equi-

librium equations among the fluid species. It is best suited to studying species distribution

in those cases in which there may be mineral assemblages that buffer the fugacities of some

of the fluid species. An alternate approach is to seek the species distribution that minimizes

the Gibbs free energy of the fluid. This is an efficient way of studying species distribution

as a function of the bulk composition of the fluid, and of identifying the conditions under

which saturation of condensed phases may take place.

9.6.1 The chemical equilibrium approach to fluid speciation

Consider a homogeneous gas phase composed of c system components, in which there are s

distinct chemical species (or phase components). The speciation problem consists of finding

the equilibrium mol fraction, X

, i =1...s, of each of the s chemical species. We therefore

need s linearly independent equations relating these variables. There must be s −c linearly

independent conditions of homogeneous equilibrium in the gas phase (Section 6.1.3 .). Each

of these equations corresponds to a balanced chemical reaction among a subset of chemical

species. The homogeneous gas phase is a system with f = c + 2 − 1 = c + 1 degrees

460 Thermodynamics of planetary volatiles

of freedom. Therefore, at constant temperature and pressure it is necessary to specify the

value of c −1 intensive variables in order to fully determine the thermodynamic state of the

system. These could be, for instance, the values of the fugacities of c −1 of the fluid species.

The fluid could exist at equilibrium with a mineral assemblage that buffers these fugacities,

or we could just specify their values arbitrarily and see how fluid speciation changes in

response to changes in these variables. Alternatively, the c −1 intensive variables could be

mol fractions of c −1 system components, which fully specify the bulk composition of the

fluid phase. In either case we have so far identified a total of: s −c +c −1 =s −1 linearly

independent equations. The final equation required to solve for the species distribution is

the closure condition,



=1. Finding the species distribution consists of writing each

of these equations, and solving the system.

Worked Example 9.6 Species distribution in C–O–H fluids, (i): general relations

Fluids in which the only, or at least major, components are C, O and H are important in

many planetary environments. In this case we have c = 3, so in order to fully specify the

thermodynamic state of the system, and thus be able to calculate the species distribution

in the fluid, we need to specify the values of c −1 = 2 intensive variables in addition to

pressure and temperature. These could be the fugacities of two of the species in the fluid,

or the bulk contents of two of the system components, say C and O (H content then follows

by difference). We shall see examples of both approaches, and why we would choose one

or the other.

In order to calculate species distribution we must begin by deciding which species are

present, or likely to be present, in the fluid phase. There are no general rules on how to do

this, and the approach is largely a combination of intuition and trial and error. For example,

under most planetary conditions (the terrestrial atmosphere being the one notable exception)

oxygen fugacity is so low that it is fine to assume X

=0. This does not mean that we will

also make f (O

)=0, however. We will use oxygen fugacity as a measure of the chemical

potential of O

, while assuming that there is no free molecular oxygen. For other species

the decision may not be that simple. In this example we will assume that the C–O–H fluid

contains five species: H

O, H

,CH

,CO

and CO and we will calculate the mol fractions

of these five species over a range of conditions. Other species could also conceivably be

present in non-negligible amounts, for instance: C

,CH

O, CH

OH. If one suspects that

this may be the case, then the fugacities of these other species can be estimated a posteriori

from the calculated species distribution, and if some of the fugacities are found to suggest

non-negligible mol fractions then the offending species can be added to the list of species,

and the species distribution calculated again.

For now let us stay with the five species, H

O, H

,CH

,CO

and CO. This makes s =5,

so that there must be s −c = 2 linearly independent homogeneous equilibrium reactions,

which we can choose as follows:

+3CO

→

←

4CO +2H

O (reaction 1)

→

←

CO +3H

. (reaction 2)

Together with the condition: X (CO

) + X (CO) + X (CH

) + X(H

O)=1 and

the values of two externally controlled intensive variables, this gives us five equations that

we can solve for the five mol fractions.

461 9.6 Speciation in multicomponent volatile phases

Homogeneous chemical equilibrium is described by equation (5.22):



=0 (9.81)

where ν

is the stoichiometric coefficient of the ith species in the reaction. Substituting

(9.13) and simplifying we get the following equation for equilibrium in a homogeneous gas

phase:



1,T

+RT



ln f

=0 (9.82)

and substituting (9.5) and rearranging:



(

)

exp



−

1,T





(



)





(

)

. (9.83)

At fixed P and T the values of all of the variables on the right-hand side of (9.83) are known,

except for the fact that the φ

are functions of X

(Section 9.5.2 ). This requires an iterative

solution of the system of equations, but except for this procedural detail (9.83) is an equation

in a subset of the unknowns, X

. Each of the (s −c) homogeneous equilibrium conditions

gives rise to an equation of this form. Incorporation of the externally controlled intensive

variables is accomplished by some modification of (9.83), as we shall now see.

Worked Example 9.7 Species distribution in C–O–H fluids, (ii): inorganic methane production by

serpentinization of ultramafic rocks

The Martian atmosphere contains trace amounts of methane (Krasnopolsky et al., 2004).

Because atmospheric methane decomposes by photodissociation over times many orders

of magnitude shorter than the age of the Solar System, the observation implies that there

is active methane outgassing from the Martian surface or subsurface. One possibility is

microbial activity (Chapter 14).Another possibility is that methane is produced by inorganic

reactions involving hydration of ultramafic rocks in the presence of a carbon-bearing fluid.

The process consists of reduction of CO

to CH

by H

generated by serpentine-producing

reactions, and is thought to be important in the Earth’s ocean floor. We will calculate

the species distribution in C–O–H fluids in equilibrium with ultramafic rocks undergoing

serpentinization. The output of the exercise will be plots of fluid species distribution as a

function of f(O

) and f (H

O), at constant temperature and pressure.

We choose to specify the values of the two intensive variables f (O

) and f (H

O) because

during serpentinization f (H

O) may be buffered by reactions such as (9.15), whereas f (O

)

may be buffered by silicate-oxide reactions such as (9.18). If f (H

O) is specified arbitrarily

then X(H

O) is given by equation (9.5):

. (9.84)

462 Thermodynamics of planetary volatiles

In order to incorporate f (O

) we write the equilibrium:

2CO +O

→

←

2CO

(reaction 3)

from which, by using (9.83) and simplifying, we get:





1/2

exp



−

0,3

1,T



. (9.85)

Applying (9.83) to each of the two homogeneous equilibrium reactions, 1 and 2 in Worked

Example 9.6, we get:

(

)

















−2

exp



−

0,1

1,T



(9.86)

and:













−1

exp



−

0,2

1,T



. (9.87)

Finally, the closure condition is:

=1. (9.88)

Equations (9.84)–(9.88) areour five equations in the five unknown mol fractions. The system

of equations does not have an analytical solution, and the fugacity coefficients are functions

of the fluid composition. The strategy to solve the system of equations is to calculate first

the standard state fugacity coefficients, use these to solve for an initial set of mol fractions,

use these mol fractions to calculate fugacity coefficients in the mixture (e.g. with (9.80)if

the RK EOS is chosen), recalculate mol fractions, and iterate between these last two steps

until consecutive solutions converge within a desired interval. An implementation in Maple

is discussed in Software Box 9.3.

Software Box 9.3 Calculation of fluid speciation by chemical equilibrium

The Maple worksheet eq_fluid_species.mw contains procedures that calculate

fluid speciation in a C–O–H fluid as a function of f (O

) and f (H

O), at constant

temperature and pressure. The procedures are written specifically to solve the problem in

Worked Example 9.7. Because in this case we choose f (O

) and f (H

O) as independent

variables the system of equations can be simplified considerably. First, the mol fraction

of H

O is calculated from (9.84), and the mol fraction of H

from:





1/2

, (S9.3.1)

where K

is the equilibrium constant for the reaction:

→

←

.(I)

463 9.6 Speciation in multicomponent volatile phases

This reduces the problem to a system of three equations in three unknowns:



·f



1/2

III





3/2





(S9.3.2)

=1 −X

−X

where K

and K

III

are the equilibrium constants for the reactions:

2CO +O

→

←

2CO

(II)

and:

+3/2O

→

←

CO +2H

O. (III)

Note that the equations appear to be linear but they are not, because the fugacity coef-

ficients are functions of composition. The system is solved with Maple’s fsolve

command. There are two procedures.

COH1 solves the fluid speciation as a function of log f (O

), at constant temperature,

pressure and H

O fugacity. It calculates an arbitrary number of points within

a specified log f (O

) interval. The procedure is invoked with the follow-

ing parameters, in this order: (pressure in bar, temperature

in centigrade, H

O fugacity in bar, initial log

oxygen fugacity, final log oxygen fugacity, number

of points to be calculated, name of output file).

COH2 solves the fluid speciation as a function of f (H

O), at constant tem-

perature, pressure and oxygen fugacity. It calculates an arbitrary number

of points within a specified f (H

O) interval. The procedure is invoked

with the following parameters, in this order: (pressure in bar,

temperature in centigrade, initial H

O fugacity in

bar, log oxygen fugacity, final H

O fugacity in bar,

number of points to be calculated, name of output

file).

Thermodynamic properties of the gas species are entered in the spreadsheet

RefStateData, with a Shomate-type heat capacity equation, as explained in Soft-

ware Box 1.1. The properties used in this example can be imported in tab-delimited

format from the file agaspeciesdata, or they can be copied from a spreadsheet.

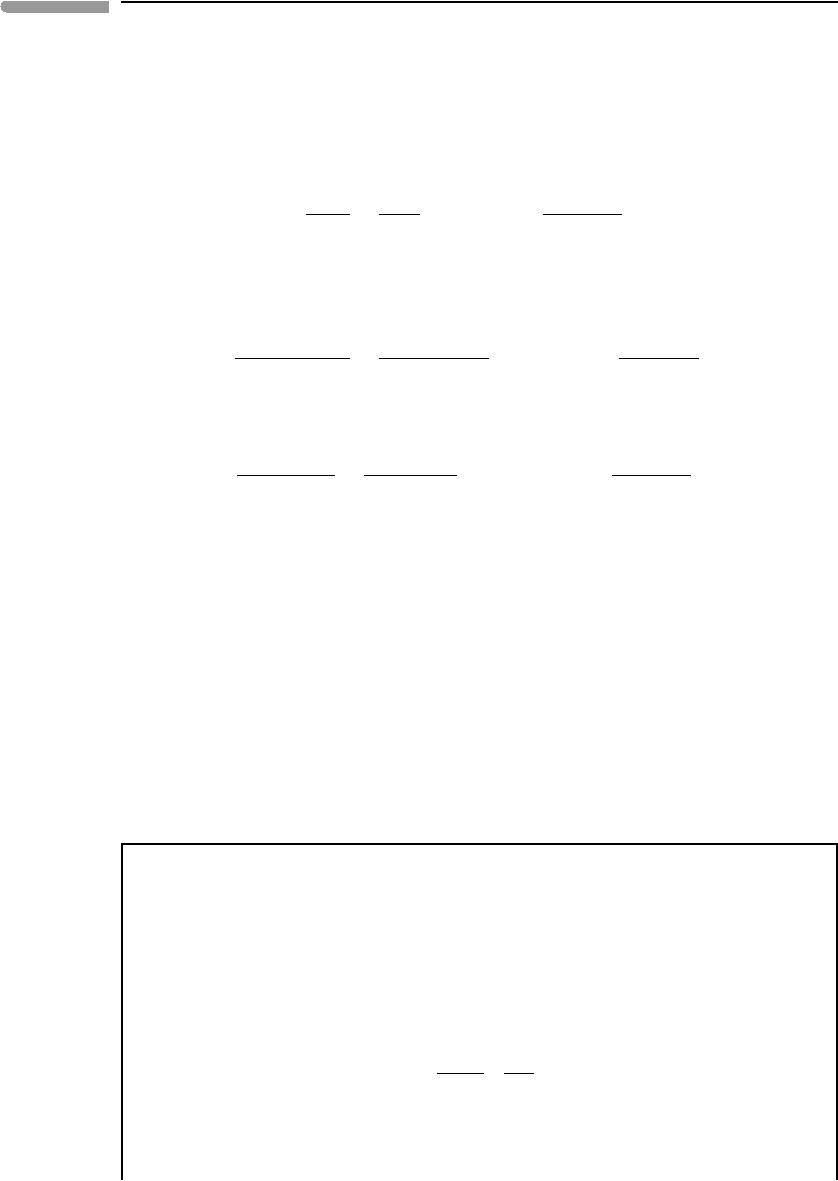
An example of the results generated by the Maple procedure is shown in Fig. 9.15. All

calculations were done at 2 kbar and 400

◦

C. I chose these conditions as representative

of serpentinization at shallow depth in the Earth’s oceanic crust. Similar conditions may

exist in the Martian crust if some type of magmatic activity survives to this day. The top

diagram shows species distribution as a function of oxygen fugacity, calculated at constant

f (H

O)=230 bar. The serpentinization reaction (9.15) buffers the fugacity of H

O at values

ranging from 215 bar for X

= 0.9 to 250 bar for X

= 0.8, corresponding to possible

464 Thermodynamics of planetary volatiles

–1

–2

–3

–4

–5

–6

–1

–2

–3

–4

–5

–6

log f(O

)bar

f(H

O) bar

f(H

O) = 230 bar

f(O

) =10

–29

bar

0 200 400 600

2 kbar - 400°C

SRP

–35

–30 –25

QFM

Fig. 9.15 Species distribution in a C–O–H ﬂuid at 2 kbar and 400

◦

C. Top: as a function of f (O

)atf (H

O) buffered by

serpentinization reaction (9.15) with X

≈0.9. The QFM and HM oxygen buffers are shown for reference. Bottom: as

a function of f (H

O) at the f (O

) of the QFM buffer. H

O fugacity at the serpentinization reaction shown by “SRP”.

Standard state fugacity of H

O at these conditions is 717 bar. Voluminous production of inorganic methane is possible

as long as oxygen fugacity stays below that of the QFM buffer.

terrestrial and Martian compositions, respectively (Exercise 9.10) – 230 bar is in the middle.

The approximate locations of the QFM and HM oxygen buffers are shown by the dashed

vertical lines. Under oxidizing conditions the fluid is a rather dull binary mixture of CO

and H

O, with vanishingly small contents of other species. At very reducing conditions

the fluid can be considered a ternary mixture of CH

O and H

. It is an empirical

observation that most terrestrial upper mantle rocks crystallized within a relatively nar-

row range of oxygen fugacity, roughly between 0.01–1 times QFM. The Martian mantle

appears to be slightly more reducing than this. Fluid speciation undergoes interesting and

rapid changes in the neighborhood of these conditions. Assuming that mantle assemblages

buffer oxygen fugacity during serpentinization, the fluids would be dominated by CH

with a mol fraction of H

Oof∼0.15 and much smaller concentrations of H

,CO

and CO.

However, within one order of magnitude of the QFM buffer, towards more oxidizing con-

ditions, CH

concentration drops rapidly, and is replaced by CO

as the dominant carbon

species.

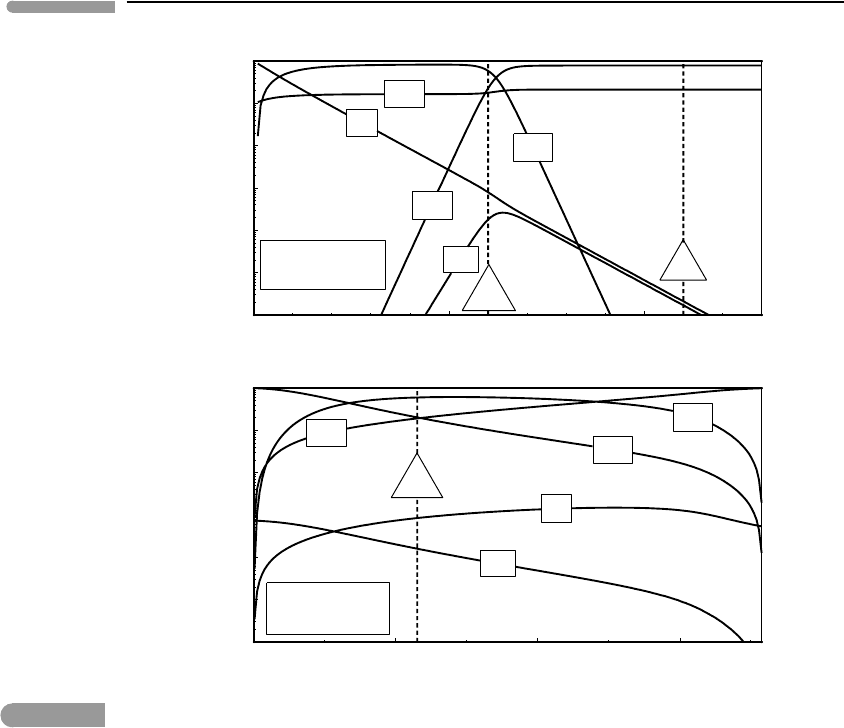
465 9.6 Speciation in multicomponent volatile phases

The effect of H

O fugacity at constant f (O

)=10

−29

bar (≈ QFM) is shown in the

bottom diagram of Fig. 9.15. The standard state H

O fugacity at 2 kbar and 400

◦

C is 717 bar

(calculated with the RK EOS), and this is the upper bound of the horizontal coordinate axis

in the figure (for which X

→ 1). The assemblage forsterite + enstatite + chrysotile

buffers f (H

O) at ∼230 bar, shown by the vertical line labeled SRP. H

O fugacity can be

greater than this if one or both of the anhydrous silicates are absent, whereas chrysotile

would not be present at equilibrium if f (H

O) was less than this value (see also Fig. 9.1).

At the oxygen fugacity of the QFM buffer CH

is the dominant species over a wide range of

O fugacities. It is replaced by H

Oasf (H

O) →f

O), i.e. as the fluid approaches

pure H

O, and by CO

as f (H

O) → 0. At these oxidation conditions H

and CO are

always minor species. In fact, CO concentration is always vanishingly small at this pressure

and temperature, and ignoring this species would have a negligible effect on the results

(Exercise 9.11).

The calculations summarized in Fig. 9.15suggest that inorganic methane production in the

shallow Martian crust is feasible, and perhaps capable of explaining the observed methane

concentration in the Martian atmosphere. This conclusion, however, rests on five premises:

(1) that ultramafic rocks are present in the shallow Martian crust, (2) that a shallow heat

source exists, (3) that a source of H

O exists, (4) that a source of CO

exists and (5) that

the ultramafic assemblage buffers oxygen fugacity to conditions not much more oxidizing

than QFM. Of these, we can be reasonably confident of (3) and, by analogy to terrestrial

examples, perhaps of (5) as well. Sedimentary carbonates could be a source of CO

, but

confirming their presence in Mars has been elusive; (1) and (2) are likely to remain unknown

until geological and geophysical work on the surface of Mars become possible, which, in

the humble opinion of this pundit, will require the development of highly mobile robots

capable of autonomous intelligent decision making.

9.6.2 Calculation of fluid speciation by Gibbs free energy minimization

There are instances in which one wishes to know how speciation in a fluid depends on its

bulk composition, rather than on externally buffered chemical potentials of some of the

species. Although it is in principle possible to use the chemical equilibrium approach to do

this, it rapidly becomes unwieldy and a much simpler method is available. It relies on the

fact that the thermodynamic potential of a system takes its minimum value at equilibrium.

As in the previous example, we consider a fluid composed of c system components. In this

instance it is convenient to choose elements as system components, for example, C, H, O,

N, S, Cl, F, etc. The total mol number (number of gram atoms) of the j th system component

will be represented by N

, j = 1...c. There are also s distinct chemical species (phase

components), with the mol number of species i labeled n

i = 1...s. If we call the total

number of mols of phase components in the fluid phase n

, then:



i=1

, X

. (9.89)

Let us write the chemical potential of the ith species as follows:

=µ

0,i

1,T

+RT ln





+RT ln





. (9.90)

466 Thermodynamics of planetary volatiles

The total Gibbs free energy of the fluid phase is given by equation (5.27):

fluid



i=1

0,i

1,T

+RT



i=1





+RT



i=1





. (9.91)

The equilibrium fluid distribution at constant temperature and pressure is given by the set

of n

s that minimizes its Gibbs free energy.

The problem of determining the fluid speciation consists of finding the minimum of the

function (9.91). Since this is a function of s variables it has s partial derivatives, relative

to each of the n

s. If an absolute minimum of the function exists it would correspond to

a point where all of the partial derivatives vanish. We do not seek the absolute minimum

of (9.91), however, because there are constraints on the values that the n

s can take. These

constraints are given by the bulk composition of the system. Recalling that N

is the total

number of atoms of the j th system component we can define C new functions that describe

the bulk composition constraints, as follows:

=RT





i=1

−N



=0, (9.92)

where η

is the number of atoms of component j in species i, and I have multiplied by RT

because it leads to a more compact final equation. The problem now consists of finding

the set of n

s that minimize (9.91), subject to the n

s also satisfying (9.92). A simple

yet powerful technique exists to solve this problem, known as the method of Lagrange

multipliers. The method consists of multiplying each of the C functions (9.92) by a constant,

(the Lagrange multiplier), adding these C new functions to (9.91) to construct a new

function, Γ , as follows:

Γ =G

fluid



j=1

(9.93)

and then minimizing Γ . The mathematical justification of the method is not complicated

but is beyond the scope of this book–aparticularly clear explanation can be found in the

textbook by Sokolnikoff and Redheffer (1966).

The function Γ has i partial derivatives relative to the n

s, which must all vanish simul-

taneously at a minimum. Performing the algebra (which you should verify for yourself) we

find that each of these equations is of the form:

∂Γ

∂n

0,i

1,T

+1 +ln





+ln





−



j=1

=0 (9.94)

where I have divided by RT in order to make the equation more readable (since we are

equating to zero this is always legal). At constant temperature and pressure we have a

total of s equations like (9.94) plus c equations (9.92), with a total of s + c unknowns:

the sn

s and the cλ

s(n

is given by (9.89)). The remarkable fact is that this system of

equations is generally quite easy to solve numerically, as we shall see in the following exam-

ple. The Lagrange multipliers have mathematical meaning, but they do not have physical

meaning in this instance and we will just discard those values. We are only interested in

the n

467 9.6 Speciation in multicomponent volatile phases

The Gibbs free energy minimization method does not require that we find homoge-

neous equilibrium equations among the fluid species, but it does require that we decide

beforehand on which species are likely to be present. However, adding or removing species

simply consists of adding or removing equations like (9.94), and making the necessary

modifications to the constraining equations (9.92). Of course, the phase rule must always

be obeyed and it is necessary to check on this before attempting to solve the system of

equations. If we restrict the system of interest to a homogeneous fluid phase with c compo-

nents then in order to completely specify the thermodynamic state of this system we must

specify the values of c +1 intensive variables. Two of these are pressure and temperature,

leaving c −1 intensive variables to be specified. These typically would be bulk compo-

sition parameters of the fluid. Alternatively, we may be interested in speciation in a fluid

phase saturated with some specific condensed phases, in which case we must minimize the

Gibbs free energy of a heterogeneous system, including the Gibbs free energy contribu-

tion of the condensed phases. The best way to understand all of this is with an example,

as follows.

Worked Example 9.8 Species distribution in C–O–H fluids, (iii): fluid composition during core

formation in planetesimals

Meteorites preserve evidence that planetesimals with radii of order 10

km underwent

core formation very early in the history of the Solar System. The chondritic precursors of

differentiated planetesimals may have been rich in carbon and H

O, so that C–O–H fluids

may have been present during core formation. The bulk compositions of these putative

fluids are unknown, but we are interested in understanding how species distribution in them

may have varied over a range of bulk compositions, and also as a function of temperature

and pressure. The Gibbs free energy minimization method is well suited to address these

questions.

As in previous examples, we shall assume that the fluid consists of the five species: CO

CO, CH

and H

O. If we consider only a homogeneous C–O–H fluid phase then this is

a ternary system with four degrees of freedom, of which two are temperature and pressure.

We can specify the other two as bulk composition variables, for example the ratios N

and N

. Note that these two ratios completely define the bulk composition of the fluid.

Because graphite is present in many differentiated and undifferentiated meteorites, however,

it is of interest to study the fluid distribution in C–O–H fluids saturated in this phase. In this

case we have a ternary system with two phases and three degrees of freedom, in which we

can specify only one compositional variable. Given that the system is saturated in graphite,

carbon is present in excess, so that we must choose the ratio N

as the compositional

variable. Molecular O

will be assumed to be present in vanishingly small amounts, which

leads to a simple way of calculating its chemical potential (or fugacity) as part of the Gibbs

free energy minimization exercise.

We begin by writing the three constraining bulk composition equations, (9.92):

=RT



graphite

−N



=RT



+2n

−N



=RT



+2n

−N



≈RT



−N



=0.

(9.95)