Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

448 Thermodynamics of planetary volatiles

as both b

and b

are negative constants. The physical meaning of the b parameter is

thus not the excluded volume. As a consequence the first term in (9.58) is not a repulsive

term, which is the intention in cubic equations of state such as MRK EOS. Second, the

terms in inverse powers of V may look like virial terms, but rigorously they are not, as

virial coefficients are defined on the basis of a series expansion of residual Helmholtz free

energy (equation (9.44)), which is not the case in equation (9.58). The BW EOS is an

empirical equation that fits the results of molecular dynamics calculations very well, and

also reproduces isolated data points for H

O volumes at extreme pressures (350 kbar), but

it has no obvious physical justification. Its one drawback is that it does not work below 10

kbar, which is a minor (but not fatal) inconvenience in the calculation of thermodynamic

functions such as fugacity. It is not known whether an equation of this type works for other

fluids too. EOS based on molecular dynamics simulations for H

O as well as for other

species of geological interest have also been proposed by Duan and co-workers (see, for

example, Duan et al., 1992, 1996, 2000; Zhang & Duan, 2009).

9.4.6 Summary

The preceding list does not come close to being an exhaustive compilation of available

equations of state. I have chosen to discuss these particular EOS either because they are

important from a historical point of view (VDW), because they have been shown to perform

adequately up to temperatures and pressures corresponding to the Earth’s upper mantle (KJ)

or the Earth’s mantle transition zone (PS and BW), or because they are a reasonable (or

only) “stopgap” EOS for some species, that can at leastprovide semi-quantitative predictions

(RK). Figure 9.11 compares four of these EOS for H

O and three of them for CO

(the BW

EOS is not calibrated for CO

) from 1 bar to 300 kbar, and at 1000 K and 2000 K. The

RK and KJ EOS are not expected to yield accurate results over most of this pressure range

but are included for comparison. Both of them predict strongly incompressible fluids. This

arises from the repulsive term in cubic EOS, which becomes unphysical at high density.

The BW and PS EOS avoid this problem and are in generally good agreement with each

other and with high pressure experimental data (see Brodholt & Wood, 1993 and Pitzer &

Sterner, 1994). The PS EOS has two advantages, however: (1) it works continuously from

the ideal gas limit to very high pressure, whereas the BW EOS breaks down below 10 kbar,

and (2) it is calibrated for both H

O and CO

The plots in Fig. 9.11suggest that at densities of up to ∼2.5–3 times the critical density

the departure of the RK EOS from the PS EOS is rather small. One could then, tentatively

and rather carefully, suggest that the RK EOS might be used for other fluid species too at

conditions such that ρ < 3ρ

. For those gases listed in Table 9.1that may conceivably exist

as free species in planetary interiors this possible upper validity bound for the RK EOS

corresponds approximately with the P –T conditions of the base of the Earth’s continental

crust. The two last columns in the table show densities calculated at 10.7 kbar and 950 K

with the RK EOS, and the ratio of these densities to the corresponding critical densities. The

latter values generally fall in the region where the RK EOS for H

O and CO

begin to depart

significantly from the corresponding PS EOS. The RK EOS is by no means accurate, but it

may provide a reasonable first-order approximation to the behavior of fluids at P<10 kbar

in those cases in which other EOS are not available.

The densities listed in Table 9.1offer a glimpse into the nature of deep planetary volatiles.

These are dense supercritical fluids. The density of supercritical H

O at the base of the

Earth’s continental crust is approximately the same as that of liquid H

O on the Earth’s

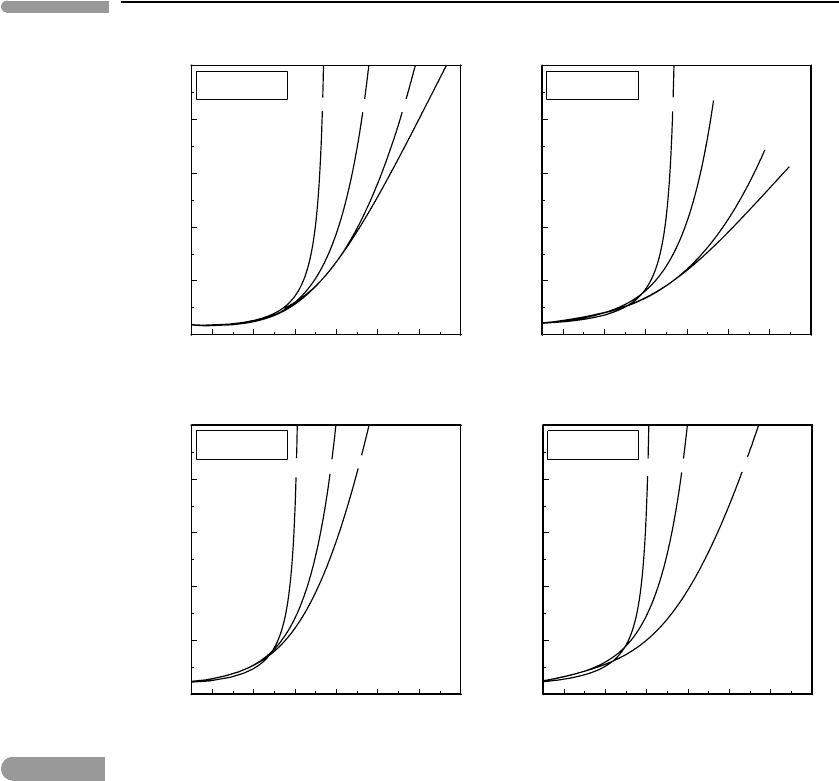
449 9.4 Equations of state for real ﬂuids

KJ BW

123 4 5 6 7

lll

-1000 K

-2000 K

-1000 K

1gcm

–3

2gcm

–3

3gcm

–3

1gcm

–3

1gcm

–3

1gcm

–3

2gcm

–3

2gcm

–3

2gcm

–3

3gcm

–3

lll

KJ PS

ρ /ρ

Fig. 9.11

Comparison of various equations of state for H

O (top) and CO

(bottom), for pressures ranging from 1 bar to 300 kbar

(coordinate axes as in Fig. 9.10, actual ﬂuid densities added for comparison). The RK EOS is not accurate above a few

kbar, and the KJ EOS may be valid to a few tens of kbar. Both the PS and BW EOS are supposed to be valid to

∼300 kbar, but at densities above ∼5 times the critical density they predict signiﬁcantly different densities for H

(the BW EOS is calibrated for H

O only).

surface. Supercritical CO

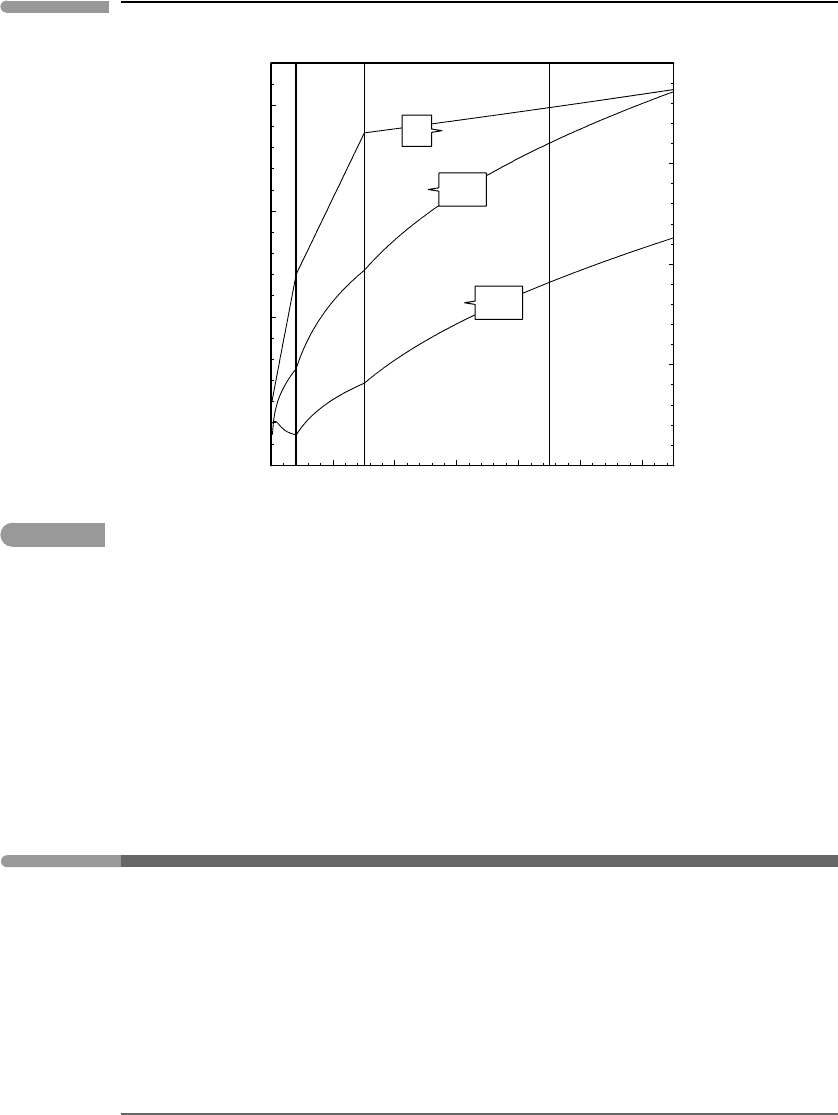
at those conditions is even denser. A more complete view is

presented in Fig. 9.12, in which I have plotted the densities of H

O and CO

along a

possible terrestrial continental geotherm, also shown in the figure. The conductive portion

of the geotherm is constructed by fixing the temperature at 300 K at the surface, 950 K at

the Moho (40 km depth) and 1650 K at the base of the lithosphere (150 km), with pressure

calculated as in Worked Example 8.3. This is physically unrealistic because it causes a

discontinuity in thermal gradient at the Moho, but the curve as a whole approximately

mimics the curved steady-state geotherm of a crust with radioactive heat production (see

Turcotte & Schubert, 2002, Chapter 4). The adiabatic geotherm at depths greater than

150 km was calculated with (8.70). The densities of H

O and CO

were calculated with

the PS EOS which is thought to be reliable at least to pressures of the base of the mantle

transition zone (∼240 kbar, Fig. 8.11). The densities of H

O and CO

at those conditions

450 Thermodynamics of planetary volatiles

0 100 200 300 400 500 600

1.5

2.5

Depth (km)

Fluid density (g cm

–3

)

500

1000

1500

2000

Temperature (K)

continental crust

mantle lithosphere

asthenosphere

mantle

transition zone

Fig. 9.12

Densities of H

O and CO

calculated with the Pitzer–Sterner EOS along a possible terrestrial geotherm, from the

surface to the top of the Earth’s lower mantle.

are approximately 1.85 and 2.55 g cm

−3

, respectively. The minimum in H

O density at

the Moho may simply be an artifact of the strong thermal gradient assumed for the crust,

which causes thermal expansion to outpace compression, but the existence of this minimum

under certain circumstances cannot be ruled out. Dense supercritical fluids such as those

represented in this figure are powerful solvents. In nature they do not exist as pure fluids,

but rather as complex solutions of silicate, oxide, carbonate and other species, with densities

higher than those shown in Fig. 9.12.

9.5 Calculation of fugacity in ﬂuid phases

In Section 9.1we defined fugacity and we saw that it is straightforward to calculate the

fugacity of a fluid species in equilibrium with a buffering solid assemblage. Those values

by themselves do not tell us much about the nature of a putative fluid in equilibrium with the

solids. They are best understood as a measure of the chemical potential of the fluid species

relative to its 1 bar standard state. A different problem is that of calculating the fugacities

of chemical species in a fluid phase, and the distribution of chemical species in the fluid.

We now address these questions.

9.5.1 Standard state fugacity of pure fluids

Standard state fugacity is calculated by substituting an equation of state in (9.11). Because

equations of state are generally pressure explicit we cannot integrate directly, so we fol-

low the same procedure that we used to calculate the pressure integral for solid phases

451 9.5 Calculation of fugacity in ﬂuid phases

(equation (8.45)). Integrating (9.11) by parts we get:

RT ln f

=PV

P ,T

−V

1,T

−



P ,T

1,T

PdV. (9.61)

Note that, in contrast to the integral for solid phases, we cannot drop the V

1,T

term (which

is multiplied by 1 bar) because for a gas the difference between 1 bar and zero pressure is

not negligible. Once a particular EOS is chosen the integral is easily implemented in Maple

(Software Box 9.1). The procedure entails, first, solving the EOS for V

P ,T

and V

1,T

and

then using these values to calculate the definite integral. We can also make the substitution,

valid at the ideal gas limit, V

1,T

≈ RT ; the result is numerically indistinguishable from

calculating V

1,T

explicitly with the EOS. If the EOS is written in terms of density, ρ, rather

than molar volume then 9.61is easily converted to:

RT ln f

P ,T

−

1,T



P ,T

1,T

dρ. (9.62)

Software Box 9.1 Calculation of standard state fugacities

The package fluideos.mw contains procedures that calculate pressure, volume and

standard state fugacity with the equations of state discussed in Section 9.4. Pressure

is calculated directly, volume is calculated by invoking Maple’s numerical solver,

fsolve, to solve the corresponding EOS for V, and standard state fugacity is cal-

culated either by performing the integral (9.61), or, for the Pitzer–Sterner EOS, with

(9.62) and (9.63). The units that must be used in every case are cm

mol

−1

for molar

volume, Kelvin for temperature and bar for pressure and fugacity. Conversion to or from

other units must be handled by the calling procedure. Particular care must be exercised

with the volume units, which are different from the ones used in other thermodynamic

calculations in this book (i.e. J bar

−1

mol

−1

). The reason for this is that use of cm

mol

−1

is deeply ingrained in the literature of thermodynamics of fluids, and the parameters for

the various EOS are almost always given in these units.

There are slight differences in the way each procedure must be invoked, which are

explained as comments in the Maple code. Some additional notes follow.

For the Van der Waals EOS there are procedures to calculate pressure and volume

only (no fugacity calculation). The values of the a and b parameters must be provided

by the calling procedure.

For the Redlich–Kwong EOS the calling procedure must provide the values of the

a and b parameters and, for calculation of volume and fugacity, an initial volume

guess. This is required in order to force the solution to the liquid or gas branch of

the loop. The actual value of the volume guess varies with each gas species and with

the specific P –T conditions. Some trial and error may be necessary (an inappropriate

volume guess will generate an error message). The Maple code listing includes some

suggestions.

Two sets of procedures are provided for the Kerrick and Jacobs EOS, for H

O and

. The EOS parameters are included in the package, so they are not passed by the

calling procedure. An initial volume guess is required for calculation of volume and

fugacity (see above).

452 Thermodynamics of planetary volatiles

Software Box 9.1 Continued

The procedures for the Brodholt–Wood EOS (for water only) should only be used

for P>10 kbar, as the equation is not valid at lower pressures. Standard state fugacity

is calculated by adding the Kerrick–Jacobs fugacity at 10 kbar to the Brodholt–Wood

integral from 10 kbar to the pressure of interest. The EOS parameters are included in

the package, so they are not passed by the calling procedure. The initial volume guess

is included in the procedure and is not passed by the calling procedure either.

Two sets of procedures are provided for the Pitzer–Sterber EOS, for H

O and CO

The EOS parameters are included in the package, so they are not passed by the calling

procedure. Pressure is calculated as a function of density, not volume, but this does

not affect the procedures that calculate volume and standard state fugacity. An initial

volume guess is required for calculation of volume and fugacity (see above).

An accompanying Maple worksheet named fluidtest.mw includes examples of

the use of the procedures in fluideos.mw.

If an explicit expression for Helmholtz free energy is available (as in the case of the PS

EOS) then a further simplification is possible, as the PdV integral can be evaluated as

follows:



P ,T

1,T

dρ =−



P ,T

1,T

PdV =



P ,T

1,T

dF = F

P ,T

−F

1,T



P ,T

−F

1,T



ideal



P ,T

−F

1,T



res

=RT ln

P ,T

1,T



P ,T

−F

1,T



res

(9.63)

At the ideal gas limit we have ρ

1,T

= 1/RT and (F

1,T

)

res

= 0, so this expression

simplifies to:

−



P ,T

1,T

PdV = RT ln

P ,T



P ,T



res

(9.64)

and, substituting in (9.62):

ln f

RT ρ

P ,T

+lnρ

P ,T



P ,T



res

+lnRT −1, (9.65)

where (F

P ,T

)

res

is given by an equation such as (9.55).

Other procedures to calculate standard state fugacities, which rely on calculating the

fugacity coefficient rather than the fugacity itself, are commonly found in the literature.

I believe that such procedures are largely a product of the time before easily accessible

computers, because their chief advantage is that they facilitate graphic integration. I find

them to be unnecessarily confusing, as implementing (9.61)or(9.65) in a symbolic algebra

software package is straightforward.

453 9.5 Calculation of fugacity in ﬂuid phases

Worked Example 9.4 Standard state fugacities of H

O and CO

0 2000 4000 6000 8000 1000

0.6

0.8

1.2

1.4

1.6

1.8

P (bar)

0 2000 4000 6000 8000 1000

P (bar)

O -1000 K

-1000 K

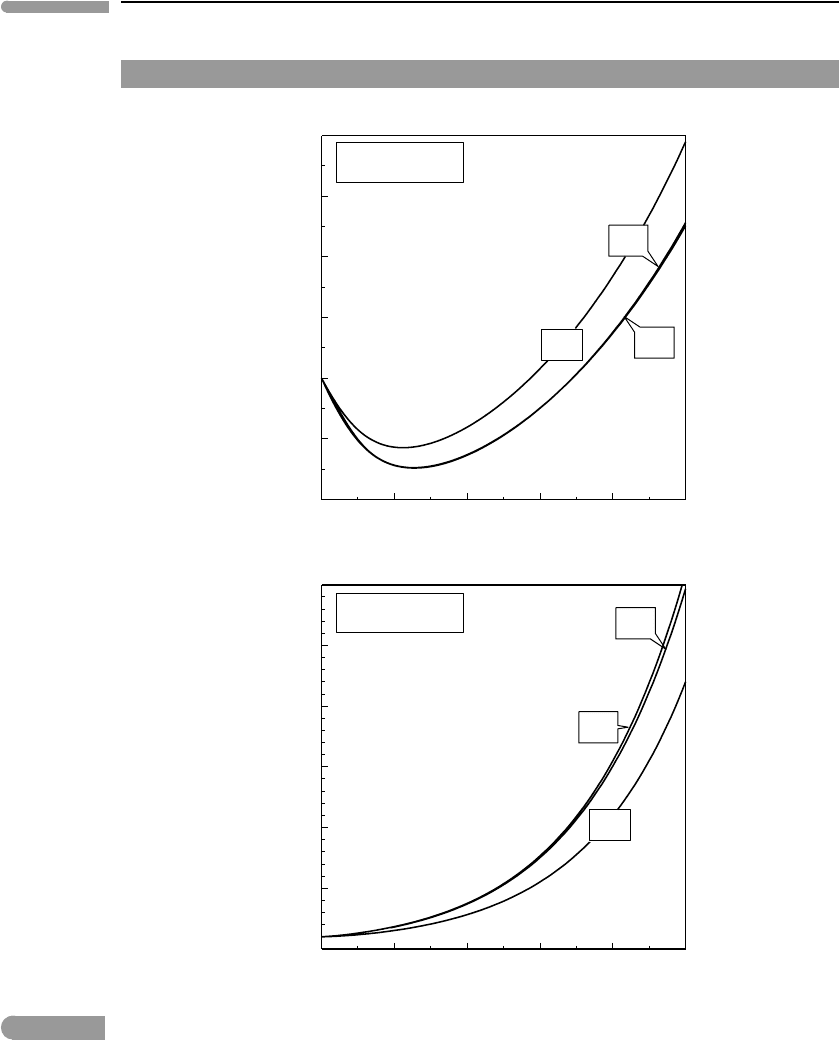
Fig. 9.13 Standard state fugacity coefﬁcients for H

O and CO

as a function of pressure at T = 1000 K, calculated with the

Redlich–Kwong, Kerrick–Jacobs and Pitzer–Sterner EOS.

Figure 9.13shows standard state fugacity coefficients for H

O and CO

at 1000 K, calcu-

lated from 1 bar to 10 kbar with the RK, KJ and PS EOS. Over this pressure range the

results for the last two EOS are for all practical purposes identical. The RK EOS predicts

noticeably different fugacities beginning at pressures of ∼1 kbar, and, relative to the other

two equations, its performance is generally better for H

O than for CO

. Note that fugacity

454 Thermodynamics of planetary volatiles

coefficients are about one order of magnitude greater for CO

than for H

O, so that the

thermodynamic effective pressure of CO

is many times higher than its actual pressure. The

two gases also behave differently in the sense that there is a pressure range, below about

7 kbar, in which fugacity coefficients of H

O are less than 1, but this is never the case for

. This difference arises from the stronger attractive term of H

O, which overwhelms

repulsion at low densities.

9.5.2 Fugacities in mixed fluids

Calculation of chemical equilibrium between a mixed volatile phase and solid or melt

phases, as well as determination of the distribution of species in a homogeneous volatile

phase at equilibrium, requires knowledge of the fugacity of each of the individual chemical

species that make up the phase. Derivation of the necessary equations is rather tedious,

and can become quite cumbersome depending on the EOS that one chooses to use, but

implementation of the final equation in Maple is generally straightforward. We begin with

equation (9.4), for the chemical potential of species i in a mixed fluid. Differentiating

relative to P, and keeping in mind that φ

is a function of pressure but X

is not, we get:



∂µ

P ,T

∂P



=RT

∂ ln





∂P

. (9.66)

But:



∂µ

P ,T

∂P



(9.67)

where v

is the partial molar volume of species i in the mixture (equation (5.37)). From

(9.66) and (9.67) we get:

RT ln φ

P = RT ln



dP, (9.68)

which is equivalent to (9.11) but written in terms of partial molar properties. The problem

is that integrating this expression is not as simple as integrating (9.11). In that case V is the

volume of the gas phase. The integrand in equation (9.68) is the partial molar volume of a

specific component of the gas phase. This generally varies with pressure, temperature and

composition, so what is required in order to integrate (9.68) is an EOS that accounts for the

effects of these variables on partial molar volume, and that can do so continuously over the

integration interval [1, P ].

As usual when working with partial molar properties, the simplest way to include the

effect of phase composition is by converting to extensive properties. From the definition of

partial molar properties, equation (5.28), we write:



∂V

∂n



P ,T ,n

j=i

(9.69)

455 9.5 Calculation of fugacity in ﬂuid phases

where V

is the (extensive) volume of the gas mixture. Now, from partial derivative

identities (equation 1.3.19 ) we find that:



∂V

∂n



P ,T ,n

j=i

=−



∂V

∂P



T ,n



∂P

∂n



V ,T ,n

j=i

(9.70)

which allows us to change the variable of integration in (9.68), as follows:

RT ln φ

P =−



P ,T

1,T



∂P

∂n



V ,T ,n

j=i

. (9.71)

This equation is general and rigorously complete , but in order to evaluate the integral we

need an explicit expression for (∂P/∂n

), and no general expression of such type exists,

as it is obviously dependent on a particular EOS. Therefore, a specific expansion of the

derivative must be found for each particular equation of state. In the following example

I illustrate the procedure with the Redlich–Kwong EOS. The procedure for other EOS is

analogous, but can be more time consuming and fill many more pages.

Worked Example 9.5 Species fugacities in a mixed Redlich–Kwong fluid

We begin by re-writing the Redlich–Kwong EOS, (9.49), in terms of the (extensive) total

volume of the gas mixture V

= nV , where V is the molar volume of the mixture, and

n =



is the total number of mols in the mixture:

P =

nRT

−nb

−

1/2

(

+nb

)

. (9.72)

The RK parameters a and b in this case describe the mixed gas phase, not a specific species.

As we shall see, determining reliable values for the mixture parameters is the main difficulty

in calculating fugacities in mixed fluids. Using (9.72) we calculate the integrand in (9.71),

which is:



∂P

∂n



V ,T ,n

j=i

(

−nb

)

+nRT



∂

(

)

∂n



(

−nb

)

−

1/2







(

+nb

)



∂





∂n



−n



∂

(

)

∂n



(

+nb

)







(9.73)

This expression allows us to evaluate the definite integral in (9.71). Below I present the

final result, recast in terms of the molar volume of the mixture, V = V

/n, and including

several simplifications that arise from the fact that, at the lower limit of integration (ideal

gas at 1 bar), the following approximations are true to an excellent degree of accuracy:

1,T

+b ≈ V

1,T

−b ≈ V

1,T

≈RT ,

1,T

≈0. (9.74)

456 Thermodynamics of planetary volatiles

The definite integral in (8.71) is, then:

RT ln φ

P = RT ln



P ,T

−b





∂

(

)

∂n



P ,T

−b



∂





∂n



nbT

1/2



P ,T



−



∂

(

)

∂n



1/2



P ,T



−



∂

(

)

∂n



1/2



P ,T



(9.75)

Equation (9.75) is specific to the RK EOS, and it still contains derivatives for which we

must find explicit values. These values depend on how the parameters a

and b

for each

of the individual species in the gas mixture combine to yield the a and b parameters for the

mixture. From a physical point of view the question that we are asking is how attraction and

repulsion among molecules of different gases depend on the properties and concentration

of each of the gases in the mixture. This is akin to finding an expression for excess mixing

properties in a crystalline solution (e.g. Section 5.9.3 ). For gases the problem is often

expressed algebraically by means of mixing rules, which are functions of the form a =

f(a

) and b =f(b

). Many mixing rules have been proposed, with greater or lesser

amounts of theoretical justification and experimental verification. In general, microscopic

mixing rules that describe interatomic potentials tend to be the ones with greater theoretical

justification, but they can only be used with EOS constructed on the basis of molecular

dynamics simulations, such as those of Brodholt and Wood and Duan and collaborators.

Mixing rules for macroscopic EOS are largely empirical. For two-parameter cubic EOS

such as the RK EOS the following mixing rules, due originally to van der Waals, are widely

used and reasonably successful:

b =



(9.76)

a =







1/2

. (9.77)

The intuitive justification for these mixing rules is easy to see. Equation (9.76) states that

the excluded volume of the mixture is the weighted average of the excluded volumes of

the individual components, whereas (9.77) states that the attractive term is the weighted

average of attractions over all types of molecular pairs. Both rules recover the corresponding

parameters for pure species. The fact that they are intuitively reasonable, however, does

not mean that they are theoretically justified, nor that they are the only rules that yield

empirically acceptable results. We will use (9.76) and (9.77) in this example, but it must

be understood that if any other set of mixing rules is to be used then the equations that

follow must be modified accordingly (as (9.72) through (9.75) must be modified for any

EOS other than the RK EOS). From (9.76) and (9.77) we obtain the following values for

the derivatives:

∂

(

)

∂n

(9.78)

∂





∂n

(

)

1/2







1/2

, (9.79)

457 9.5 Calculation of fugacity in ﬂuid phases

where the summation in (9.79) is over all components in the mixture, i.e. including com-

ponent i (it is a good idea to work out the derivatives on your own to see why this is so).

Substituting in (9.75) we arrive at:

RT ln

=RT ln φ

P = RT ln



P ,T

−b



P ,T

−b

(

)

1/2







1/2



P ,T



−

1/2



P ,T



−

1/2



P ,T



(9.80)

It is important to understand how this equation must be used. The calculation procedure

starts with the composition of the mixed gas phase (i.e. the values of X

for all component

species), uses these mol fractions to calculate a and b of the mixture with (9.76) and (9.77),

then these parameters are used to calculate the molar volume of the mixture at P and T , V

P ,T

with the RK EOS, equation (9.49), and finally the values for the mixture (a,b,V

P ,T

) are

combined with a

, b

of the species of interest in (9.80), to calculate the fugacity coefficient

and fugacity of species i.AMaple implementation is discussed in Software Box 9.2.

Software Box 9.2 Calculation of fugacities and fluid speciation in mixed fluids

The Maple package RKmixing.mw contains procedures that calculate species fugac-

ities in a mixed fluid containing an arbitrary number of species, by using the

Redlich–Kwong EOS and mixing rules given by equations (9.76) and (9.77). The mixing

rules are implemented in procedures bmix and amix, and the derivative of the a mixing

rule (equation (9.79), converted to mol fraction as in (9.80)) in procedure damix. The

package also contains procedures that calculate volume and fugacity with the RK EOS,

identical to those in fluideos.mw and included here for convenience only.

Procedure rkphimix is the key to this package. It calculates the fugacity coefficient

of the ith species using equation (9.80). The call to this procedure is rkphimix(X,

a, b, i, P, T, vguess), where:

X is a one-dimensional array containing the mol fractions of all species in the mixture

a is a one-dimensional array containing the RK a parameters, in the same order as X

b is a one-dimensional array containing the RK b parameters, in the same order as X

i is the index of the species of interest in the arrays (i.e. the identity of the species

for which the fugacity coefficient is to be calculated)

P and T are pressure in bar and temperature in Kelvin

vguess is an initial guess for the volume of the mixture (trial and error may be

necessary).

The procedure returns the fugacity coefficient of species i.

The Maple worksheet phimixcalc.mw shows an example of the use of procedure

rkphimix. It calculates fugacity coefficients and fugacities, and the ratio of each of

these variables to the corresponding standard state value (as plotted in Fig. 9.14) for a

binary join. The example is for the H

O–CH

join in the figure. In order to calculate

some other join the RK parameters must be changed in the procedure itself, as explained

in the Maple code.