Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

428 Thermodynamics of planetary volatiles

The effect of pressure on oxygen fugacity along the three buffering reactions at a constant

temperature of 1000

◦

C is shown in the bottom panel of Fig. 9.3. From 1 bar to 100 kbar

(which is within the range of pressures that Holland and Powell’s data base is expected

to be reliable) oxygen fugacity along the QFI buffer reaction stays several orders of mag-

nitude below the other two, but the QFM and HM buffers intersect at P ≈ 57 kbar. This

is an intersection between two pseudounivariant reactions (Section 6.3.1 ), that defines a

pseudoinvariant point. The HM reaction is degenerate, so it crosses the pseudoinvariant

point without becoming metastable, but the QFM reaction must become metastable at the

pseudoinvariant point. Two other reactions, magnetite-absent and oxygen-absent, must also

radiate from the pseudo-invariant point. These reactions, shown in Fig. 9.3 in their correct

calculated locations, are:

2Fe

SiO

→

←

2Fe

+2SiO

(9.20)

2Fe

+SiO

→

←

2Fe

+Fe

SiO

. (9.21)

The first reaction is an analog to the QFM buffer which is not stable in the Earth’s crust

and shallow mantle, but that can be expected to substitute for QFM as the oxide–silicate

buffer at greater depths. The second reaction is called an iron disproportionation reaction.

It entails no change in oxidation state, but rather the segregation of Fe

and Fe

, that

occur together in magnetite, into a ferric phase (hematite) and a ferrous phase (fayalite).

Because it is oxygen-absent it plots parallel to the f (O

) axis.

9.2 Liquid–vapor equilibrium. Critical phase transitions redux

In Section 1.15, see in particular Fig. 1.16, we saw that non-ideal gases span a range of

densities between those of ideal gases and liquids. In order to develop equations of state

appropriate for non-ideal gases, then, we must first discuss the nature of the liquid–gas

phase transition in some detail. We recall that gases are non-condensed fluids because

they expand indefinitely as pressure decreases, whereas we call liquids condensed fluids

because they do not behave in this manner. A vapor is a gas in equilibrium with its liquid.

As temperature increases, the properties of liquid and vapor at equilibrium approach each

other, until the two phases become indistinguishable at the critical temperature. Above the

critical temperature a single fluid phase is stable, called a supercritical fluid. The density of

supercritical fluids may vary from values typical of liquids to values typical of ideal gases.

The defining property of a supercritical fluid is that in it there is no discontinuous phase

transition separating both states. This behavior is reminiscent of that of solid solutions and

order–disorder transitions in crystalline solids (Chapter 7).

9.2.1 The van der Waals equation of state

Ideal gases do not condense at any temperature or pressure, as by hypothesis they lack

intermolecular forces. Thus, in contrast to the ideal gas EOS, we require that any EOS for

a real gas be able to reproduce condensation and the existence of a critical phase transition.

The simplest equation of state that can achieve this was proposed by the Dutch physical

chemist J. D. van der Waals in 1873. The van der Waals EOS is not quantitatively accurate,

429 9.2 Liquid–vapor equilibrium

but thanks to its simplicity and its correct qualitative behavior it remains a powerful tool

with which to gain insight into the behavior of real fluids. Some of the more refined EOS

that we will discuss in later sections follow the van der Waals equation in spirit, if not in

algebraic detail.

We begin by defining the (poorly named) compressibility factor of a gas, Z, as follows:

Z ≡

. (9.22)

For an ideal gas, Z = 1. In a real gas we expect that there are both attractive and repulsive

forces between molecules, that are not present in an ideal gas. Intermolecular repulsion will

cause Z to increase, whereas attraction will cause it to decrease. We can then write Z for a

real gas as follows:

Z = 1 +Z

repulsion

−Z

attraction

. (9.23)

The idea behind van der Waals’equation, and in fact behind most EOS for real gases, is to find

explicit expressions for the Z terms that match the experimentally measured behavior of

fluids over as wide a range of conditions as possible. Many successful approaches, beginning

with that of van der Waals himself, entail some combination of intuition, educated guesses

and trial and error.

As both the repulsive and attractive terms arise from intermolecular potentials, it is

reasonable to postulate that the two Z terms will vary inversely with some power of

volume: the closer the molecules are, the stronger they will interact. This is essentially the

same argument used to derive the Mie EOS, e.g. equation (8.47). Note that, just as in that

case, the qualitative statement about the relationship between volume and intermolecular

potentials says nothing about the actual value of the exponents. The van der Waals EOS

assumes that both the attractive and repulsive terms go as V

−1

, but the value of the exponent

could be different, and in fact this is one of the problems with this equation.

Real gas molecules have a finite volume, which in the van der Waals equation is defined

as the distance at which intermolecular repulsion becomes infinite: no matter how high

we make the pressure we cannot squeeze molecules any closer than this value. The total

molecular volume defined in this way for a mol of gas is called the excluded volume and

symbolized with b. We write the repulsive term as follows:

Z

repulsion

V −b

. (9.24)

This equation gives the desired behavior: repulsion becomes stronger with decreasing vol-

ume, and diverges as the excluded volume is approached (the term b must appear in the

numerator too because Z is a dimensionless number). We can immediately see two pitfalls

in this equation: first, molecules are assumed to be perfectly rigid, and second, the effect of

temperature, which is likely to affect the b parameter, is ignored. We shall return to this in

later sections.

In contrast to repulsion, the effect of attractive forces is assumed to decrease with

increasing thermal agitation, so we write:

Z

attraction

RT V

, (9.25)

where a is a constant with the units required to make Z non-dimensional. Again there are

pitfalls that we will address later: a is assumed to be independent of temperature, and the

430 Thermodynamics of planetary volatiles

exponents of T and V are arbitrarily assumed to be −1. Ignoring all of these problems we

substitute in (9.23) and obtain:

Z = 1 +

V −b

−

RT V

, (9.26)

which, by using (9.22), we recast as follows:

P =

V −b

−

. (9.27)

Equation (9.27) is the van der Waals EOS. We shall now see what this equation predicts

about the behavior of fluids, following a path that parallels our prior discussions of critical

phase transitions in Chapter 7.

9.2.2 The critical point of a van der Waals fluid

For a system at equilibrium the derivative (∂P /∂V )

must be negative. This is easy to

prove formally from the equilibrium conditions for Helmholtz free energy (Exercise 9.4),

but we can also accept it on the grounds of physical intuition: in a system at equilibrium

volume can only decrease in response to an increase in pressure. For the ideal gas EOS

this condition is always true, but the van der Waals EOS may have a positive (∂P /∂V )

derivative under certain circumstances. To see why, and what these circumstances may be,

we differentiate (9.27):



∂P

∂V



=−

(

V −b

)

. (9.28)

It is obvious that (9.28) may take positive or negative values, according to the relative

magnitudes of T and V. Inside any T –V region over which the derivative is positive a single

fluid phase cannot exist at equilibrium (note the emphasis on single). In order to identify

such regions we note that the derivative vanishes where it changes sign, so we make (9.28)

equal to 0 and solve for T:

T =

(

V −b

)

. (9.29)

The shape of this function is shown in Fig. 9.4. The origin of the coordinate system is fixed

at T = 0 and V = b, as the region V<bis not physically meaningful. By construction,

(∂P /∂V )

vanishes along the curve, it is negative for temperatures above the curve and

positive for temperatures below it. Thus, the region under the curve in Fig. 9.4 is the

T –V region within which a single fluid cannot exist at equilibrium, which I will call the

“prohibited region”.

The peak of the curve is the maximum temperature at which (∂P /∂V )

may take non-

negative values. For temperatures higher than this value, let us call it T

, (∂P /∂V )

negative for all values of V. This means that for T>T

a single fluid phase that obeys van

der Waals’ EOS (equation (9.27)) is stable for all V and P. By “being stable for all V and P ”

I mean that we can vary the intensive variables continuously and, as long as we stay inside

the region T>T

there will be no discontinuity in the material properties of the phase. We

shall return to this, but for now we notice that the properties of equation (9.27) assure us

that this continuity is certainly true of density.

431 9.2 Liquid–vapor equilibrium

V=b

Single phase not stable within this region

Fig. 9.4

Conditions for reversal of the sign of the derivative (∂P/∂V)

for a van der Waals gas. In the shaded region below

the curve the derivative is positive, implying that a single ﬂuid phase cannot be stable. The peak of the curve is the

critical temperature: above this temperature a single ﬂuid phase of any density can be stable.

For T<T

there is a “prohibited” volume (or density) interval within which a single

phase is not stable. Any volume inside this region can, however, be obtained algebraically as

a linear combination of two arbitrary volumes outside and on opposite sides of the curve – in

particular, by two volumes that satisfy equation (9.27) at the same temperature and pressure

(the equation is cubic in V, so it must have either one or three real roots). Note that these

volumes are not the two intersections of a temperature coordinate with the curve in Fig. 9.4,

as these intersections simply define the condition (∂P /∂V )

= 0. The two volumes that

we seek correspond to two stable phases of different densities, so they must lie outside of

the curve, and they must be such that they minimize the free energy of the system. We shall

return to this crucial point shortly.

At the temperature T

the system changes from one in which two different fluids are

possible (for T<T

) to one in which only one fluid is possible (for T>T

). This looks a

lot like a critical temperature, and in fact it is. In order to find its value we need to locate

the maximum of the curve in Fig. 9.4, so we differentiate (9.29) and equate to 0:



(

V −b

)

−3

(

V −b

)



=0. (9.30)

The solution to (9.30) is the critical volume V

, i.e. the volume at the critical temperature:

=3b. (9.31)

Substituting in (9.29) we get the critical temperature, T

27Rb

(9.32)

432 Thermodynamics of planetary volatiles

and using (9.31) and (9.32)in(9.27) we get the critical pressure, P

27b

. (9.33)

The set {T

} gives the coordinates of the critical point of a van der Waals gas with

constants a and b. In the next section we will show rigorously that a single supercritical fluid

phase is stable at T>T

, whereas two subcritical phases, a liquid and its vapor, can exist at

equilibrium for T<T

.At the temperature T

the properties of the subcritical phases become

identical, marking the critical phase transition. Before we demonstrate these conclusions

formally it is important to focus on some of the similarities between the critical point of a

fluid and those that we discussed in Chapter 7, for solutions and for order–disorder phase

transitions in crystals.

We recall that the Helmholtz free energy, F, is a function of the natural variables T and

V, such that (see Section 4.8.6 ):



∂F

∂V



=−P . (9.34)

Thus:



∂

∂V



=−



∂P

∂V



(

V −b

)

−

(9.35)

and:



∂

∂V



=−

2RT

(

V −b

)

. (9.36)

Substituting the values of T

and V

we find that both the second and third derivatives of

free energy vanish at the critical point. This is the same behavior that we found at the critical

point of a solution, and at order–disorder critical phase transitions in general (Chapter 7). We

recall that the order parameter is a quantity that vanishes at the critical point and takes non-

zero values only for T<T

. For example, the difference in the compositions of coexisting

phases or the difference in the dimensions of the crystallographic axes. For a fluid we

may take the difference in density, or molar volume, between the two subcritical phases,

liquid and vapor, as the order parameter (see Fig. 7.8). Note also that, because the second

derivative of free energy (=−∂P /∂V ) vanishes at the critical point, so does the isothermal

bulk modulus. Equivalently, the compressibility becomes infinite. Divergence of quantities

such as compressibility and heat capacity (Fig. 7.9) is a characteristic of critical phenomena.

9.2.3 The phase diagram of a van der Waals fluid

To continue our study of real fluids it is best to recast van der Waals’ EOS into non-

dimensional form. We define the non-dimensional pressure, π, volume, φ, and temperature,

τ, as the ratios P /P

, V/V

and T/T

, respectively. The variables π, φ and τ are also known

as reduced variables (do not confuse this φ with the fugacity coefficient that we defined in

Section 9.1). With these coordinate transformations the van der Waals EOS becomes:

π =

8τ

3φ −1

−

. (9.37)

433 9.2 Liquid–vapor equilibrium

1234

–1

1234

–1

=1.5

=0.7

τ = 0.7

∂π /∂φ

critical point

(a)

(b)

τ =1

τ = 1.5

Fig. 9.5

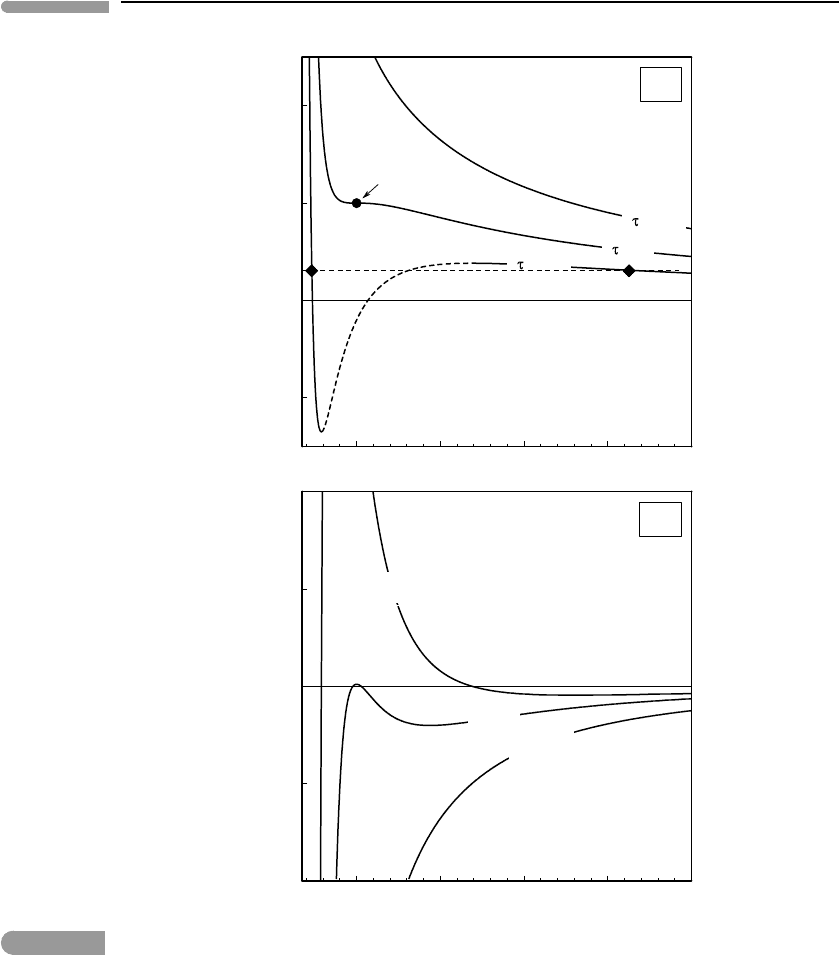
Reduced pressure of a van der Waals gas (a) and its volume derivative (b), plotted as a function of reduced volume.

For a given temperature below the critical temperature (e.g. τ = 0.7) the width of the “prohibited” region in Fig. 9.4

corresponds to the dashed segment of the curve in (a). For any pressure between 0 and the local maximum of the

isothermtherearetwo phases atequilibrium.Anexample is shownbythetwo diamonds joinedbythethin dashed line.

Because the parameters a and b disappear in this equation, this would be a universal EOS if

all fluids followed van der Waals behavior (i.e. equation (9.26)) exactly, but unfortunately

this is not the case. We will need to develop more complex EOS to deal with real fluids in a

quantitative fashion. In the meantime (9.37) is an excellent tool with which to gain physical

insight.

434 Thermodynamics of planetary volatiles

Figure 9.5a shows π =π(φ) calculated with (9.37) along three isotherms, and Fig. 9.5b

shows (∂π/∂φ)

along the same three isotherms. The supercritical isotherm, τ = 1.5, is

reminiscent of the hyperbola P ∼ 1/V that describes an ideal gas. Its slope is always

negative, implying that a single phase of continuously variable density is stable everywhere

along the isotherm. The critical isotherm, τ =1, tends to become parallel to the supercritical

isotherm at low densities (large φ) but is generally steeper than the latter at high densities.

This hints at the existence of two distinct fluids: a highly incompressible high density

fluid for which (∂π/∂φ)

→−∞and a fairly compressible low density fluid for which

(∂π/∂φ)

approaches a small negative value (see Fig. 9.5b). One could identify the former

with a condensed phase (liquid) and the latter with a non-condensed phase (gas), but along

the critical isotherm there is continuity between both states, because there is no first-order

phase transition between them. To see this, note that the critical point, τ = π = φ = 1, is

the only point on this isotherm for which (∂π/∂φ)

= 0 and, since this point corresponds

to a maximum of the first derivative function (Fig. 9.5b), the second derivative vanishes

too, as we expected from (9.36). At the critical point the bulk modulus vanishes, but since

it never becomes negative there is no region of the critical isotherm inside which a single

fluid phase is prohibited from existing.

Along the subcritical isotherm, τ = 0.7, there is an interval, shown by the broken seg-

ment in Fig. 9.5a, inside which (∂π/∂φ)

is positive, as seen in the corresponding curve

in Fig. 9.5b. This “prohibited” interval extends from a minimum to a maximum on the

isotherm, as it must given that (∂π/∂φ)

vanishes at both ends of the interval. Of course, it

is possible to have an equilibrium system with {τ,π,φ} coordinates inside this region, but

the thermodynamic relations summarized in Fig. 9.5, which we will explore in more detail

in a moment, mandate that this system cannot consist of a single phase. It must be made up of

two phases that lie on the same isotherm but on opposite sides of the prohibited region, and

at the same pressure. In this case we can identify the low-volume phase as a liquid and the

high-volume phase as its vapor. Note, however, that the diagrams in this figure by themselves

cannot tell us what the volumes of the phases that coexist at equilibrium are. In particular,

these are not the volumes at the ends of the prohibited interval, first because they do not lie

at the same pressure and second because, in this case, one of the volumes corresponds to

the unphysical condition π < 0. The latter is not a general constrain, as isotherms closer to

τ =1 never take negative π values, but the former is (as an aside, negative pressures are not

altogether impossible, but their magnitude is limited by the cohesiveness of the material).

There is a π interval, between 0 and the maximum on the isotherm located at the right end

of the broken segment, within which (9.37) has two solutions in φ for each value of π,on

opposite sides of the prohibited interval. The thin dashed line is an example, with the two

solutions shown by the diamonds. The phase rule assures us that one and only one of these

solution pairs along each isotherm represents thermodynamic equilibrium, as we have a

system of one component and two phases, and therefore one degree of freedom, which we

have chosen to be the temperature. The phase rule does not tell us, of course, which is

the equilibrium pair. What we can be certain about, however, and what characterizes the

subcritical region, is that the two phases must be separated by a first-order phase transition,

because there is a discontinuity in volume and hence in enthalpy and entropy.

In order to find the volumes of coexisting liquid and vapor at equilibrium we begin by

calculating the Helmholtz free energy of the fluid. This we do by integrating (9.34) and

substituting the van der Waals EOS (equation (9.27)). The result is (check with Maple):

435 9.2 Liquid–vapor equilibrium

F =−



PdV =−RT ln

(

V −b

)

−



+RT ln

(

−b

)



, (9.38)

where F

, V

are the Helmholtz free energy and volume at some arbitrary reference state.

Let us now define a non-dimensional Helmholtz free energy, W = F/RT

. Substituting

(9.31) and (9.32)in(9.38) we find:

W =−τ ln

(

3φ −1

)

−

8φ



+τ ln

(

3φ

−1

)

8φ



. (9.39)

We can, without loss of generality, set the constant term in square brackets equal to zero –

this will move the curve of W(φ) up or down, but will not change its geometric properties.

We also find, using the chain rule and required substitutions:

∂W

∂φ

∂W

∂F

∂V

∂φ

=−

π, (9.40)

which is the non-dimensional equivalent of (9.34).

The left-hand-side panels in Fig. 9.6show W(φ) calculated for three different values

of τ. It is now important to recall that, whereas Gibbs free energy defines the equilib-

rium condition at constant temperature and pressure, Helmholtz free energy does the same

thing at constant temperature and volume (Sections 4.8.5 and 4.8.6 ). This means that the

equilibrium state of a system at constant temperature and volume is the one that mini-

mizes Helmholtz free energy, F, or its non-dimensional avatar, W. We see in Fig. 9.6 that,

for τ > 1, i.e. above the critical temperature, the Helmholtz free energy has continuously

negative curvature, meaning that at any given volume there is only one possible stable

phase. The situation is different below the critical temperature, τ < 1. There are now two

inflection points, and two points on the curve that have a common tangent. Because the

tangent to the Helmholtz free energy curve is the negative of the pressure (equation (9.40))

the φ coordinates of these two points are the volumes of two different fluids at the same

pressure. Moreover, for all volumes in between these two the Helmholtz free energy of a

combination of these two fluids (i.e. a point on the common tangent) is lower than that

of a single fluid with the same volume, implying that the single fluid is unstable relative

to formation of liquid + vapor. The interval between φ

liq

and φ

vap

in the bottom left

panel of Fig. 9.6is thus the “prohibited” density interval. Outside of this interval Helmholtz

free energy has negative curvature and a single phase is stable, a high-density liquid or a

low-density gas.

The transition between the two different behaviors occurs at the critical temperature,

τ = 1. As the critical temperature is approached from below the common tangent points

approach one another, and merge at a single point at τ = 1. At this temperature the free

energy curve becomes “flat” in the neighborhood of the coordinate φ = 1 (the critical

volume), reflecting the fact that its second and third derivatives vanish (equations (9.35)

and (9.36)). A comparison of Fig. 9.6with Fig. 7.1should bring out the similarities between

the critical point of a fluid and the critical mixing point of a solution, but there are also

differences, most notably the fact that symmetry between the subcritical phases is never

possible in a fluid.

The diagram on the right of Fig. 9.6shows the phase relations of the fluid in terms of the

reduced variables π, φ and τ, and completes the analogy with critical mixing (Fig. 7.1). The

thick curve, called the liquid–vapor loop, bounds the “prohibited region”. Calculation of the

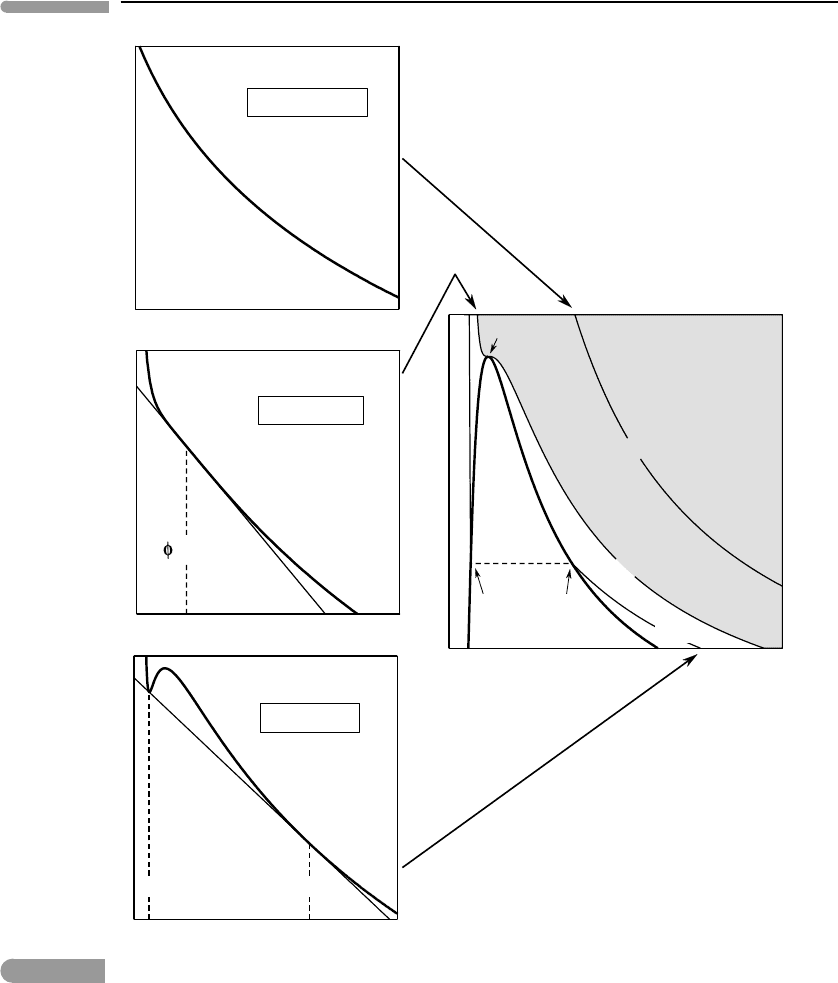
436 Thermodynamics of planetary volatiles

supercritical fluid

liq

vap

ψψ

liquid + vapor

"critical" fluid

liquid

vapor

critical point

supercritical fluid

τ = 1

τ = φ = π = 1

τ < 1

τ > 1

τ < 1

liq

Fig. 9.6

Non-dimensional Helmholtz free energy as a function of non-dimensional volume (left panels, for the critical

temperature and temperatures above and below the critical temperature), and the phase diagram of a van der Waals

gas (right panel). Compare with Gibbs free energy diagram for a non-ideal solution in Fig. 7.1.

loop is explainedin Box 9.1.Any π–φ combination inside the loop consists of liquid +vapor,

with the equilibrium volumes given by the two intersections of the pressure coordinate,

indicated by the dashed line, with the loop. The liquid–vapor loop corresponds to the solvus

in Fig. 7.1. The supercritical fluid phase unmixes into two subcritical phases as temperature

437 9.2 Liquid–vapor equilibrium

drops below T

. The width of the loop, φ

vap

−φ

liq

, is the order parameter. The thin curves

are isotherms, with the critical isotherm (τ =1) separating the supercritical region (shaded)

from the subcritical region. The critical isotherm is tangent to the liquid–vapor loop at the

critical point.

Box 9.1

Calculation of the liquid–vapor loop

The problem of calculating the liquid–vapor loop, e.g. in Fig. 9.7and 9.8, consists of ﬁnding the volumes of

the two subcritical phases at equilibrium. We seek to solve for three variables, the non-dimensional volumes

of the liquid and its vapor, φ

liq

and φ

vap

, respectively, and the non-dimensional pressure, π. Hence, we

need three independent equations, which in this case are non-linear. The ﬁrst one is the equality of pressures

between the two phases, π

liq

=π

vap

, which from (9.37) yields:

8τ

3φ

liq

−1

−

liq

8τ

3φ

vap

−1

−

vap

. (9.1.1)

The second equation is the equality of Gibbs free energy between the two phases. Note that the Helmholtz

free energy of the two ﬂuids at equilibrium is not the same – Fig. 9.6makes this clear. The two ﬂuids have

different volumes, so Helmholtz free energy does not provide the correct equilibrium criterion. The two ﬂuids

coexist at equilibrium at constant temperature and pressure, however (Fig. 9.6, right panel), so it must be

liq

vap

. Now, applying the Legendre transform we ﬁnd that:

G = F +PV (9.1.2)

so the equilibrium condition at constant P and T is:

G = F +PV =0 (9.1.3)

which in non-dimensional form becomes:

ψ +

πφ = 0 (9.1.4)

and substituting (9.39):

−τ ln



3φ

liq

−1

3φ

vap

−1



−



liq

−

vap





liq

−φ

vap



=0. (9.1.5)

The third equation is the equation of state, which we can apply to either the vapor or the liquid, e.g.:

π =

8τ

3φ

vap

−1

−

vap

. (9.1.6)

At a given temperature equations (9.1.1 ), (9.1.5 ) and (9.1.6 ) are a system of three non-linear equations in

the three unknowns φ

liq

, φ

vap

, and π . They are easily solved with a Maple procedure that you are asked to

write in Exercise 9.5. Solving for the vapor–liquid loop with the dimensional van der Waals EOS, or any other

EOS, is in principle no more complicated.