Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

408 Equations of state for solids

because solids only have vibrational degrees of freedom, the vibrational energy density

equals the internal energy density, so that we can differentiate (8.57) as follows:



∂P

∂T





∂E

∂T



γC

. (8.60)

Comparing with (8.59) yields a definition of the Grüneisen ratio in terms of experimentally

accessible macroscopic quantities:

γ =

αK

. (8.61)

We now return to the calculation of thermal pressure. As thermal pressure is calculated

along a constant-volume path (see Fig. 8.1) we can find it by integrating (8.59):



(

αK

)

dT . (8.62)

The lower limit of integration is 0 because thermal pressure, which arises from atomic

vibrations, vanishes only at 0 K. Thus, and as I mentioned previously, in order for the

calculation to be rigorously correct isothermal compression must be calculated at 0 K.

In order to evaluate the integral (8.62) we not only need to know how the product αK

varies with temperature but also, and more subtly, how it changes with volume. The latter

information is needed even if the integration path is at constant volume because the value

of this volume will be different depending on how much the material is compressed at zero

temperature (see Fig. 8.1). From our discussion in Sections 8.2.2 and 8.2.3, see in particular

Figs. 8.2 and 8.3, we see that K

decreases linearly with temperature and, above the Debye

temperature, α increases approximately linearly with temperature. We can thus expect that

their product will not be very sensitive to temperature above θ

, and this expectation is

borne out by experimental measurements. Fig. 8.7 shows non-dimensional plots of αK

normalized to the value of this product at the Debye temperature, versus non-dimensional

temperature, T/θ

, for the same three minerals as in Figs. 8.2 and 8.3 (data from Anderson

et al., 1992). Although in detail it is necessary to account for the small deviations observed

above θ

(seeAnderson, 1995), assuming that αK

is constant above the Debye temperature

is commonly an excellent approximation.

For T>θ

, which is the case for planetary interiors at depths greater than the top few

kilometers, we can break up (8.62) as follows:

(

αK

)

(

T −θ

)



(

αK

)

dT , (8.63)

where (αK

)

is the approximately constant high temperature value of αK

, for example

measured at some T above the Debye temperature. If the regular non-dimensional behavior

depicted in Fig. 8.7 is truly universal (or at least applicable to the chief minerals in deep

planetary interiors) then an additional simplification is possible. Let A

be the area under

the (nearly identical) curves in Fig. 8.7 in the interval [0,1], given by:



(

αK

)

(

αK

)





(

αK

)



(

αK

)

dT . (8.64)

409 8.4 Thermal pressure

0 0.5 1 1.5

0.5

αK

/αK

(θ

)

Forsterite

T/θ

MgO

Fig. 8.7

Variation of the product αK

, normalized to the values of the product at the Debye temperatures, relative to

non-dimensional temperature. Data from Anderson et al. (1992). The area under the curves between 0 and 1 is

approximately 0.77.

Numerical integration of the curves in Fig. 8.7 yields A

≈0.77, so:



(

αK

)

dT ≈ 0.77θ

(

αK

)

(8.65)

and, substituting in (8.63):

≈

(

αK

)

(

T −0.23θ

)

, T ≥ θ

. (8.66)

Other thermodynamic approximations to thermal pressure may be found, for example, in

Anderson (1995) and Jackson and Rigden (1996), but my approximation, equation (8.66),

appears to work reasonably well. Thermal pressures for T <θ

can be calculated in a

similar manner, by integrating numerically (8.64) to the desired temperature.

Worked Example 8.3 Thermal pressure in planetary mantles

Let us compare the relative magnitudes of thermal pressure and elastic pressure (see equation

(8.2)) along mantle adiabats. We re-write the condition of hydrostatic equilibrium (equation

(2.34)) as a function of depth, z, as follows:

=gρ =

, (8.67)

410 Equations of state for solids

where v is specific volume (i.e. volume per unit of mass). We will first calculate zero-

temperature pressure as a function of depth inside a planet by integrating this equation as

follows:

z −z



VdP, (8.68)

where P

is the pressure at some reference depth, z

. If we choose the reference depth as the

surface of the planet then z

=0, but as we shall see we cannot always do this. Whereas

in previous discussions we considered density to be a constant, we will now incorporate the

variation of density with pressure (at constant T =0). This requires a function V = V(P),

i.e. an isothermal EOS, which for this example I choose to be the Born–Mie EOS, equation

(8.56). In order to use a pressure-explicit EOS such as this one we must integrate by parts, so

we substitute (8.45)in(8.68) and, accounting for thenon-zero lower integration limit, obtain:

z = z



−P



PdV −



PdV



. (8.69)

In this equation V

is the zero-pressure volume, as usual, V

is the volume at the pressure of

depth z, and V

is the volume at the pressure of the reference depth, P

, all taken at the same

temperature, 0 K in this case. The integral is easily implemented in Maple (see Software

Box 8.3), but there is an important point that I want to stress here: equation (8.69) is a function

of the form z =z(V ). Thus, the calculation procedure requires that we choose a value of V

use this value to calculate P from the EOS (e.g. equation (8.56) if we choose the Born–Mie

EOS), and then evaluate the integral in (8.69). In other words, the independent variable in

the calculations is volume (or density), and both pressure and depth are functions of V. This

may sound odd, but it is required by the pressure-explicit nature of the equations of state.

Software Box 8.3 Calculation of zero-temperature pressures in solid planets

The Maple worksheet Z_P.mw contains two procedures that generate tables of zero-

temperature pressure and density as a function of depth, by calling on the procedures in

the S_EOS package. The two procedures, ZvsP_BoMi and ZvsP_BiMu are identical,

except that they use the Born–Mie or Birch–Murnaghan EOS, respectively. The proce-

dures use density as the independent variable, convert density to specific volume, and

calculate pressure from the equation of state and depth from equation (8.69). In order to

apply these procedures to planets with phase transitions (e.g. Fig. 8.9) the procedure is

run separately for each layer, using the pressure and depth at the bottom of each layer as

the starting point for the next layer. The material properties for each phase, molar vol-

ume and bulk modulus, are always the zero-pressure values (see discussion in Worked

Example 8.3).

If we knew nothing about phase transitions in the Earth’s mantle, or chose to ignore them,

then we could start with olivine at the Earth’s surface and solve the equations (the EOS for

P and 8.69 for z) all the way to the core–mantle boundary. Using this approach we have

=3.006×10

−4

−1

(corresponding to ρ

=3300 kg m

−3

, which is the zero-pressure

density of Fo

olivine), K

= 1.3 Mbar = 1.3 × 10

Pa, K



= 4 and z

= 0.

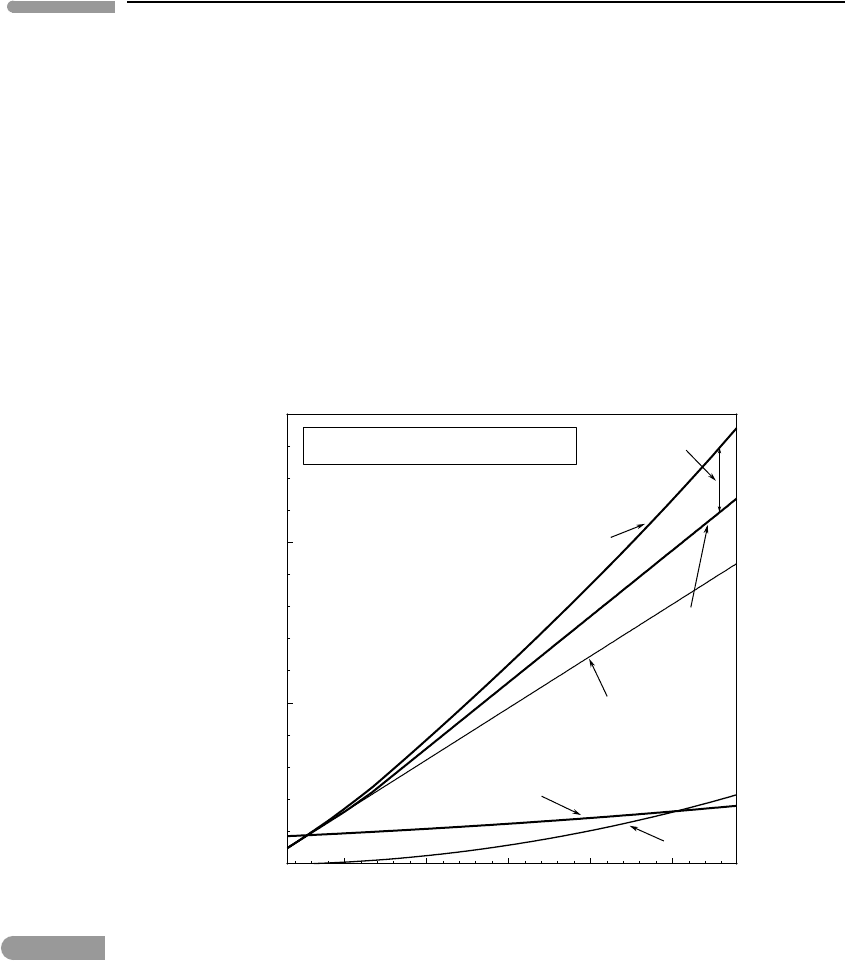
411 8.4 Thermal pressure

The resulting zero-temperature pressure vs. depth curve calculated with the Born-Mie EOS

and assuming a constant value of g = 9.8ms

−2

(see Chapter 2 for a justification of why

this is an acceptable approximation) is shown by the thin P

curve in Fig. 8.8. This curve

can’t be much better than an order of magnitude approximation, however, as both density

and bulk modulus change at mantle phase transitions.

The correct procedure is, of course, to calculate the curve in various segments, changing

the material properties at each phase transition to those of the incoming phase, and setting

equal to the depth of the phase transition and P

equal to the pressure at that depth. Note

very carefully, however, that the material properties of the incoming phase that are used to

solve the EOS and the depth equation, (8.69), are always the zero-pressure properties. If

you are not clear on why this is so you should derive equation (8.69) and convince yourself

that this is indeed the case.

500 1000 1500 2000 2500

500

1000

Depth (km)

Pressure (kbar)

PREM

(Born-Mie)

(Born-Mie - no phase transitions)

∆P

Pressure in the Earth’s mantle

Fig. 8.8 Calculated pressures in the Earth’s mantle compared to pressures on the Preliminary Reference Earth Model (PREM) of

Dziewonski and Anderson (1981). Chemical composition of the mantle is assumed to be Mg

1.8

0.2

SiO

. P

are

zero-temperature pressures calculated with the Born-Mie EOS, either ignoring olivine phase transitions (thin curve),

or assuming two phase transitions, at depths of 500 km (olivine to ringwoodite) and 670 km (ringwoodite to

perovskite + ferropericlase), see also Figure 8.9. P

is the thermal pressure calculated with equation 8.66.

Thermodynamic calculation of thermal pressure assumes heating at constant volume (see Figure 8.1). This is not

realizable in the Earth’s upper mantle and transition zone, because self-compression of the mantle is not sufﬁcient to

counter thermal expansion. The actual thermal pressure in the Earth’s mantle may be better represented by the

difference between PREM and the calculated zero-temperature pressure, shown by the curve labeled P

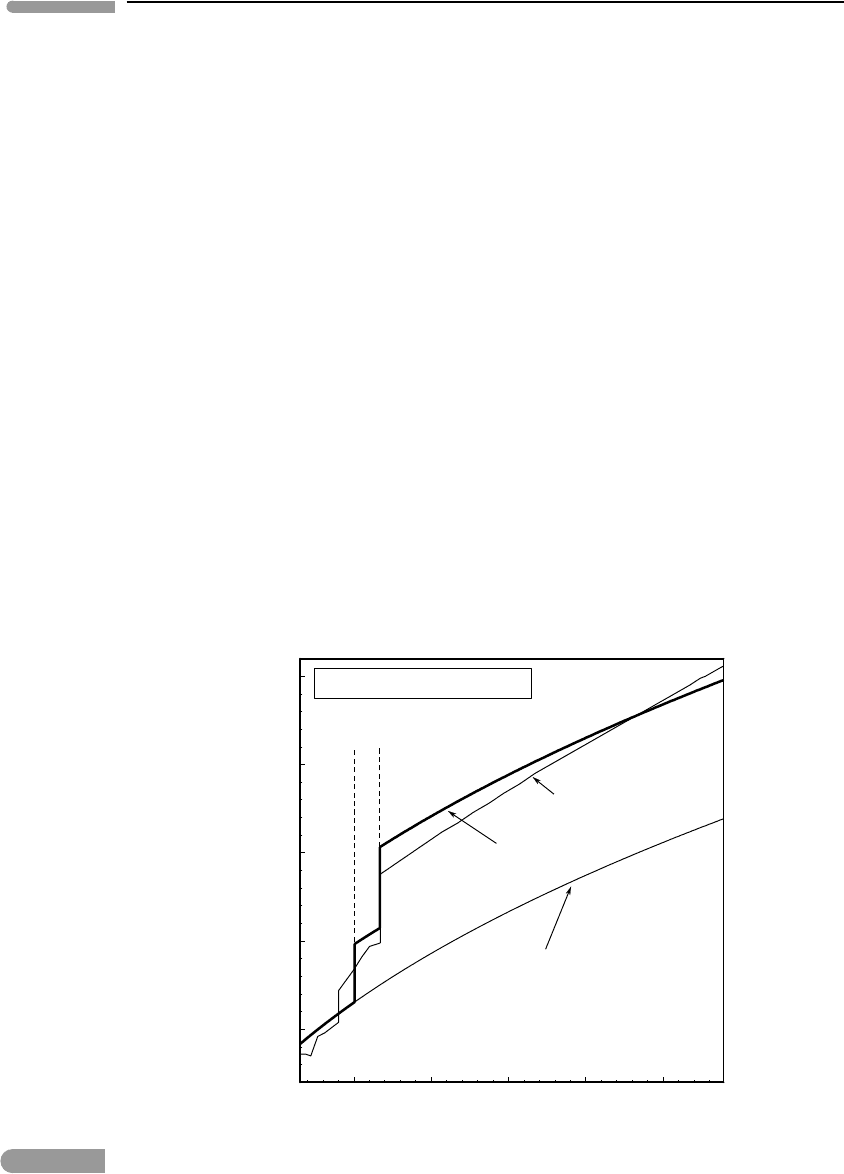
412 Equations of state for solids

The thick P

curve in Fig. 8.8 was calculated in this way, assuming that olivine transforms

to ringwoodite at 500 km depth, and ringwoodite transforms to perovskite at 660 km depth.

This is still a simplification, as it ignores other phase transitions in the mantle transition

zone (olivine transforms to wadsleyite at the top of the transition zone, ∼410 km deep), but

it is much better than assuming that olivine is stable throughout the entire mantle. Pressures

up to 500 km depth were calculated with the olivine properties given above. This yields

a pressure of 163 kbar at 500 km depth, and these values are set equal to P

and z

for

the ringwoodite layer. For ringwoodite we have ρ

= 3700 kg m

−3

, K

= 1.9 Mbar =

1.9 × 10

Pa, and K



=4. With these values we get P

=222 kbar at z

=660 km, which

is the top of the perovskite layer, and then use the zero pressure properties of perovskite,

= 4200 kg m

−3

, K

= 2.5 Mbar = 2.5 × 10

Pa, and K



= 4 to calculate pressures

all the way to the core–mantle boundary. Figure 8.9 shows zero-temperature densities as a

function of depth calculated with this model, as well as the (hypothetical) density of olivine

if phase transitions are ignored (i.e. along the thin P

curve in Fig. 8.8). Exercise 8.5 asks

you to verify these results.

Figure 8.8 shows that ignoring mantle phase transitions underestimates the pressure at

the core–mantle boundary by ∼200 kbar, or roughly 20% relative. This difference reflects

the fact that there are significant density jumps at the phase transitions, as shown by Fig. 8.9.

Also shown in Figs. 8.8 and 8.9 are curves labeled PREM. These curves show pressure and

density along the Preliminary Reference Earth Model of Dziewonski and Anderson (1981).

Details of how these values were calculated are complex and beyond the space available

here (see, for example, Anderson, 1989). Suffice it to say that the PREM results are not

500 1000 1500 2000 2500

3500

4000

4500

5000

5500

Depth (km)

Density (kg m

–3

)

Density in the Earth’s mantle

Zero-T density

(Born-Mie- no phase transitions)

Zero-T density

(Born-Mie)

PREM

olivine

ringwoodite

perovskite

Fig. 8.9 Densities as a function of depth in the Earth’s mantle calculated assuming zero-temperature compression of

1.8

0.2

SiO

, with or without phase transitions as in Fig. 8.8. Densities along PREM shown for comparison; note the

much more complicated pattern in the upper mantle and transition zone, corresponding to mineral reactions that I

ignored in the simpliﬁed calculations.

413 8.4 Thermal pressure

altogether independent of a specific choice of EOS, but they are generally accepted as a

good approximation to actual pressures and densities inside the Earth.

We first note that although PREM densities show more “texture” than the ones calcu-

lated in this example, reflecting the real phase transitions in the Earth’s mantle, they are

in generally good agreement with the simple model. PREM pressures and calculated zero

temperature pressures are virtually indistinguishable to a depth of ∼500 km, but diverge

smoothly as depth increases beyond this value. At the base of the Earth’s mantle the cal-

culated zero-temperature pressure is ∼220 kbar lower than the PREM pressure. Clearly,

thermal pressure must have a role in this discrepancy, but what exactly is this role? In order

to answer this question we calculate thermal pressure along the mantle adiabat.

Temperature along an adiabat is obtained by integrating equation (3.35), as follows:

T = T

exp



αg

(

z −z

)



, (8.70)

where T

is the temperature at the base of the lithosphere (top of the convective layer)

and z

is the depth to the base of the lithosphere. For Earth we can take T

= 1650 K

and z

= 150 km. Substituting in (8.66) we obtain an approximate expression for thermal

pressure along a mantle adiabat:

≈

(

αK

)



exp



αg

(

z −z

)



−0.23θ



. (8.71)

We now need to choose characteristic values for the parameters in this equation. For many

minerals θ

is of the order of 1000 K and the high-temperature (i.e. above θ

) values of

α and c

are approximately 3 × 10

−5

−1

and 1.2 kJ K

−1

, respectively. The high-

temperature value of αK

for closely-packed minerals is of the order of 60 bar K

−1

. Using

these parameter values equation (8.71) generates the curve labeled P

in Fig. 8.8.

A “blind” application of equation (8.2) would lead us to add P

to P

in order to obtain

the total pressure. Figure 8.8 shows that, whereas this would yield a value comparable to the

PREM pressure at the core–mantle boundary, pressures calculated in this way would become

progressively more erroneous with decreasing depth, and would be gross overestimates in

the upper mantle. What is going on here? Quite simply, that if we had applied equation

(8.2) “blindly” we would have been careless with how we applied thermodynamics to

the real world. The definition of thermal pressure (equations (8.57)or(8.59)) requires

that volume be kept constant as the material is heated, yet the Earth does not behave as

a perfectly rigid container. At shallow depth, where the zero-temperature pressure and

the (calculated) thermal pressure are of comparable magnitudes, compression of the mantle

under its own weight (often called self-compression) cannot keep the mantle from expanding

as its temperature increases. The zero-temperature (elastic) pressure corresponds to the load

that is available to keep the volume of the “container” fixed and it is not enough to counteract

the thermal expansion of the mantle. In other words, the isochoric heating leg in Fig. 8.1

is not realizable in the Earth’s upper mantle, because the upper mantle does not behave as

a rigid vessel. In particular, Fig. 8.8 suggests that at depths less than 300 km or so thermal

pressure would be higher than zero temperature pressure, which is physically impossible

(the material would shatter).

If the material is allowed to expand freely then there can be no thermal pressure. The

increase in atomic vibrational energy that occurs with increasing temperature is in such

case expressed macroscopically as thermal expansion rather than thermal pressure. The

coincidence between PREM and P

suggests that this is the case in the Earth’s upper mantle

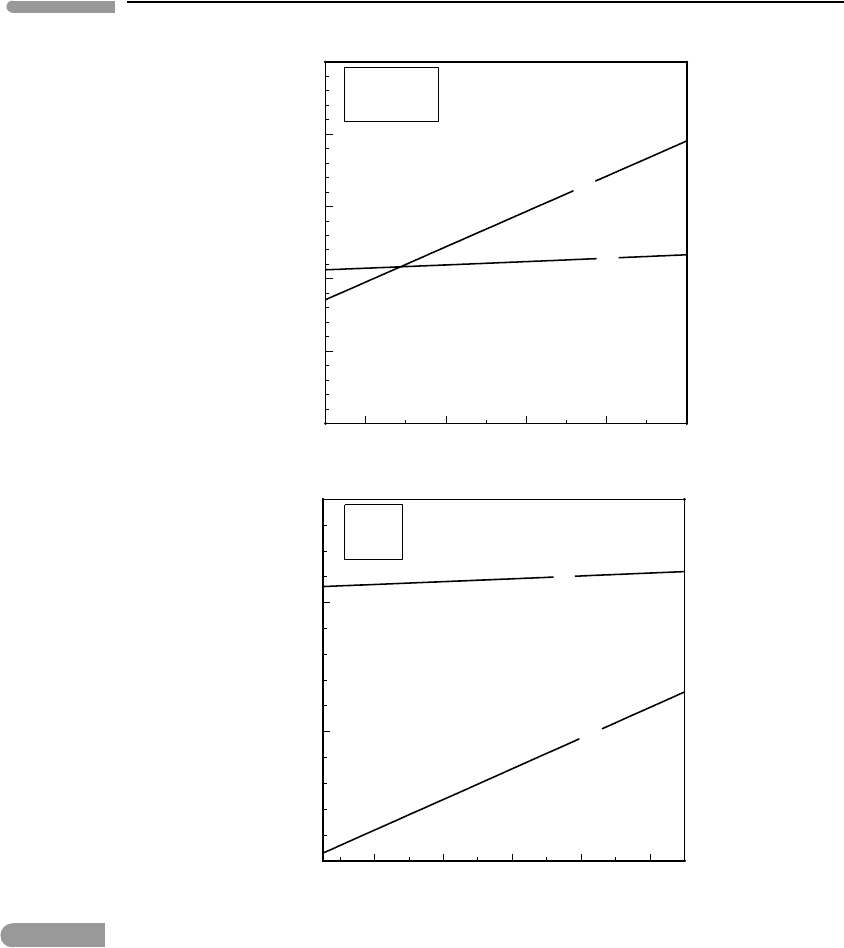
414 Equations of state for solids

800 1000 1200 1400 160

100

150

200

250

Depth (km)

Mars

200 400 600 800 1000

100

Depth (km)

Pressure (kbar)

Fig. 8.10 Zero-temperature pressures and thermal pressures (calculated with the constant-volume assumption, Fig. 8.1)in

Mars and Io. Thermal pressure is likely to be vanishingly small in Io, and almost negligible in the Martian mantle.

(depths less than ∼650 km). The picture at greater depths becomes more blurred. If PREM

is an accurate representation of actual pressures inside the Earth and P

is the correct zero

temperature pressure then the difference between the two values must be thermal pressure.

This difference, let us call it the inferred thermal pressure, is shown by the curve labeled

P

in Fig. 8.8. The inferred thermal pressure only becomes comparable to the calculated

thermal pressure at depths in excess of 1500 km or so. This suggests that at such depths

it becomes reasonable to consider the mantle as a “constant volume” vessel, and that

a direct application of equation (8.2) to calculate pressure is likely acceptable for the Earth’s

deep mantle and core. As we move towards the surface there is not enough load to keep

415 8.4 Thermal pressure

the volume perfectly constant, but neither is free expansion possible, so that some thermal

pressure builds up. This decreases with decreasing depth, until thermal pressure essentially

vanishes in the upper mantle. There is no well-defined ratio between P

and calculated P

at which the actual thermal pressure becomes significant, but Figure 8.8 suggests that when

is less than about 1/3P

, the constant volume approximation, and hence equation (8.2),

may become reasonably accurate.

What about application to other planets, for which we do not have PREM as a benchmark?

Figure 8.10 shows P

and P

calculated for the mantles of Mars and Io (core–mantle

boundaries assumed to be at 1630 km and 1100 km depth, respectively, after Lodders &

Fegley, 1998). In the case of Mars I assumed an adiabatic (convecting) mantle below

a 700 km lithosphere, with T

= 2000 K and g = 3.7ms

−2

. For Io I assumed a thin

lithosphere (z

= 50 km), with T

= 2000 K and g = 1.8ms

−2

. In both cases I assumed

that olivine does not undergo phase transitions. The case of Io is unambiguous: temperature

is high enough and gravitational acceleration low enough that calculated thermal pressure

is everywhere higher than zero temperature pressure, by a large factor. This means that Io’s

interior must behave as an essentially unconfined solid or, in other words, that pressure in

Io’s interior is well approximated by zero-temperature pressure, with a vanishingly small

thermal component. In the case of Mars we find that at the core–mantle boundary P

≈0.6

. By comparison, a similar relationship occurs in Earth at a depth of ∼600 km, where the

inferred thermal pressure, P

,is∼10 kbar, or about 5% of the zero-temperature pressure.

One could tentatively conclude that thermal pressure is generally negligible in the Martian

mantle. Thermal pressures in the Moon and Venus are left as an exercise for the reader.

Worked Example 8.4 The ringwoodite–perovskite phase transition in planetary mantles revisited

In Worked Example 8.2 we calculated phase diagrams for the Mg and Fe end-member

systems of mantle silicates. If we focus on the stishovite-absent phase boundary we see

that, in an Fe-Mg system, we can write three linearly independent heterogeneous equilibria

along this phase boundary:

(i) Mg

SiO

 MgSiO

+MgO

(ii) Fe

SiO

 FeSiO

+FeO

(iii) MgSiO

+FeO  FeSiO

+MgO. (8.72)

Excess mixing properties for perovksite, ringwoodite and periclase are not well known, and

in any case a set of mixing properties consistent with the standard state properties that I

chose to calculate the phase diagram in Fig. 8.6 does not exist (see Worked Example 5.7

for why this is important). Under these circumstances, and as a first approximation, we will

treat the three phases as being ideal solutions. Assuming that all phases are binary Mg–Fe

solutions we write the equilibrium conditions for the three reactions as follows:

(i) K

(i)

=exp



−



0,(i)

P,T



·X





416 Equations of state for solids

(ii) K

(ii)

=exp



−



0,(ii)

P,T





1 −X





1 −X





1 −X



(iii) K

(iii)

=exp



−



0,(iii)

P,T





1 −X



·X



1 −X



. (8.73)

At fixed pressure and temperature these are three equations in three unknowns, so that

we can solve for the compositions of the three phases at equilibrium. It is always a good

idea to check that this is consistent with the phase rule. In the Fe-Mg system we have F =3

and c =3, so f =2 and everything is fine – fixing two intensive variables fully determines

the thermodynamic state of the system.

Let us now calculate the composition of the phases at equilibrium at the 670 km discon-

tinuity, and compare the results to the structure and composition of the terrestrial mantle. In

order to do this we use the pressure vs. depth values from PREM (shown in Fig. 8.8), and

combine them with temperatures as a function of depth calculated with (8.70), assuming

= 1650 K at z

= 150 km. This yields a curve of pressure vs. temperature, labeled

“Terrestrial adiabat” in Fig. 8.11. Calculated conditions at the 670 km discontinuity are

∼238 kbar and ∼1600

◦

C, shown with the dash-dot lines in the figure. Using these values

in the solution of the system of equations (8.73) (Software Box 8.4) yields X

= 0.86,

= 0.9 and X

= 0.82, which compares rather favorably with the Mg number of

the terrestrial mantle of ∼90. It is hard to say to what extent this agreement is fortuitous,

but it is encouraging. If correct, it means that for the composition of the Earth’s mantle

the stishovite-absent reaction is displaced relative to the Mg end-member so that it goes

through 238 kbar at 1600

◦

C. The calculation also predicts that Fe partitions into the oxide

phase relative to the silicates, which agrees with experimental findings.

Software Box 8.4 Fe–Mg exchange among ringwoodite, perovskite and ferropericlase

Maple worksheet fe_mg_exch_hiP.mw contains two new procedures that solve the

system of equations in Worked Example 8.4 and generate the P –X loop in Fig. 8.12.

Procedure FMX calls on dgPT (see Software Box 8.2) to solve the system of non-

linear simultaneous equations (8.73), for the three unknowns X

, X

and X

Executing the statement block following the procedure runs FMX and outputs the three

mol fractions to the screen. Procedure FMX_LOOP encloses FMX in a pressure loop and

generates a file that lists the three mol fractions as a function of pressure, at constant

temperature. This output is used to construct Fig. 8.12. Remember that the statement

block at the end of the worksheet, where the reaction stoichiometries are defined, must

be executed before the Fe-Mg calculations are attempted, or an error message will result.

The attentive reader should have noticed that, given that ringwoodite–perovskite–

periclase equilibrium in the Fe-Mg system is divariant, the three phases must coexist over

a pressure range at constant temperature. This is the behavior depicted in the right hand

panel of Fig. 6.18. By solving the system of equations (8.73) for a range of pressures at a

417 8.4 Thermal pressure

1000

Pressure (kbar)

1500 2000

180

200

220

240

260

280

Temperature (°C)

Mg-rw

Mg-pv

Mg-pc

Mg-rw

Mg-pc

Fe-rw

Fe-pv

Fe-pc

[Fe]

[Mg]

Fe-rw

Fe-pc

Terrestrial adiabat

Martian adiabat

670 km discontinuity

CMB

Mg, rw

0.9

Mg, rw

0.64

Fe-pc

Fe-pv

Fig. 8.11 Terrestrial and Martian adiabats superimposed on the phase diagram of Fig. 8.6, with some reactions omitted for

clarity. The diagram predicts that stabilization of silicate perovskite in the terrestrial mantle at the 670 km

discontinuity would take place for a bulk composition with X

≈0.9, which agrees almost perfectly (and perhaps

somewhat fortuitously) with the mantle composition. The Martian adiabat terminates at the conditions of the

core–mantle boundary, shown with a star. The ringwoodite–perovskite phase transition would take place at the

conditions of the Martian core–mantle boundary for a bulk composition with X

≈0.64, which is more ferroan that

any likely Martian mantle composition. Silicate perovksite is therefore unlikely to be present in the Martian mantle.

Breakdown of ringwoodite to ferropericlase +stishovite is also unlikely if temperatures in the Martian mantle are of

the order of those estimated in Section 3.9, see also Fig. 3.18.

constant temperature (say 1600

◦

C) we can construct a pressure–composition loop such as

that in Fig. 6.18. This is shown in Fig. 8.12, but there are two complications. First, as Fig. 8.6

shows, the stishovite-absent equilibrium must become metastable at a certain X

value.

Calculation of the exact X

and P at which this happens is left as an exercise. In Fig.

8.12 I truncate the diagram at 225 kbar, which is close to the conditions at which the

stishovite-absent equilibrium becomes metastable relative to the perovskite-absent one (see

Fig. 8.6). The second complication is that, in contrast to the simple phase transitions dis-

cussed in Section 6.6, the equilibrium described by equations (8.73) has two phases with