Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

378 Critical phase transitions

The fact that this derivative is negative means four things. Firstly, that the disordered phase

is metastable at the critical temperature, because it corresponds to a maximum of G(φ).

Secondly, that if the other solution must represent the stable phase at T

, then g

must be

positive (see equation (7.59)). Thirdly, that the order parameter of the stable phase at the

critical temperature is given by (also comes from (7.59)):

φ =



−



1/2

, T = T

. (7.61)

Plugging this result in the second derivative proves that this is indeed the value of the order

parameter that minimizes the Landau potential at T

. Fourthly, and most momentously, that

the phase transition must occur at a different temperature, T

, which must be T

> T

,asthe

disordered phase can only become stable with increasing temperature, and it is not stable

at T

The critical point is in effect a metastable critical point, but for reasons that will become

clear in a moment we nonetheless wish to know the value of T

. As always, we scale to

φ =1atT =0 and, substituting in (7.59) (because the ordered phase must be the stable one

at zero temperature), we get:

. (7.62)

It is important to emphasize that (7.62) yields the temperature of a metastable critical point,

not of an actual phase transition, but note that if g

= 0 then the solution collapses to that

of the tricritical case, equation (7.54) – you may see where this is going.

At the transition temperature T

, G(φ) of the (partially) ordered phase must become zero,

because this is the Landau potential of the disordered phase everywhere above T

. But the

ordered phase must also be stable at T

, so the first derivative of the Landau potential for

the ordered phase must also vanish at T

. We thus have two equations that must vanish

simultaneously, one for G(φ) and the other one for its first derivative. Dividing the first of

these equations by φ

and the second one by φ we get:

(

−T

)

(

−T

)

=0 (7.63)

which yield the solutions:

φ =



−



1/2

, T = T

(7.64)

and:

αg

. (7.65)

Equation (7.64) says that at the temperature T

given by (7.65) the system undergoes a

discontinuous (= first-order) phase transition, as shown by the curve labeled “first order”

in Fig. 7.10. This is so because at that temperature the Landau potential of a phase that

is still partially ordered (with φ given by (7.64)) vanishes and therefore becomes equal to

the Landau potential of the disordered phase. The order parameter “jumps” from the value

379 7.6 Landau theory of phase transitions

given by (7.64) to 0 at a definite temperature, T

. The key to understanding the details of

this behavior is in the ratio (−g

). To see why we first combine (7.62) and (7.65)to

obtain:

=1 +





1 +





. (7.66)

The second equation in (7.63) is the equilibrium equation (first derivative of the Landau

potential equal to zero) so it is valid for φ = 0 for all T < T

. Using the quadratic formula

and some algebra we find that the non-zero solution is generated by the positive square root

(Exercise 7.7). By using (7.62) and some additional algebra, we then arrive at:

φ =





−









1 +



1 −





1/2





1/2

, T ≤ T

. (7.67)

We can see that as g

→ 0 the solution for the first-order phase transition approaches the

tricritical case. Equation (7.66) says that, as g

→ 0, T

approaches T

which, according

to (7.62), is the value of T

for the tricritical case (i.e. for g

→0, (7.62) becomes (7.54)).

Moreover, equation (7.67) shows that the solution for the order parameter approaches that

of the tricritical case (equation (7.55)) as g

→0.

A tricritical phase transition is therefore a limiting case, between a continuous (critical)

and a first-order phase transition. As Fig. 7.11 suggests, it shares characteristics of both:

entropy (and volume) are continuous across the tricritical phase transition, but “less smooth”

than at a critical phase transition. Heat capacity diverges, but less strongly than in a first-

order transition, and the anomaly occurs over a finite temperature interval, rather than only

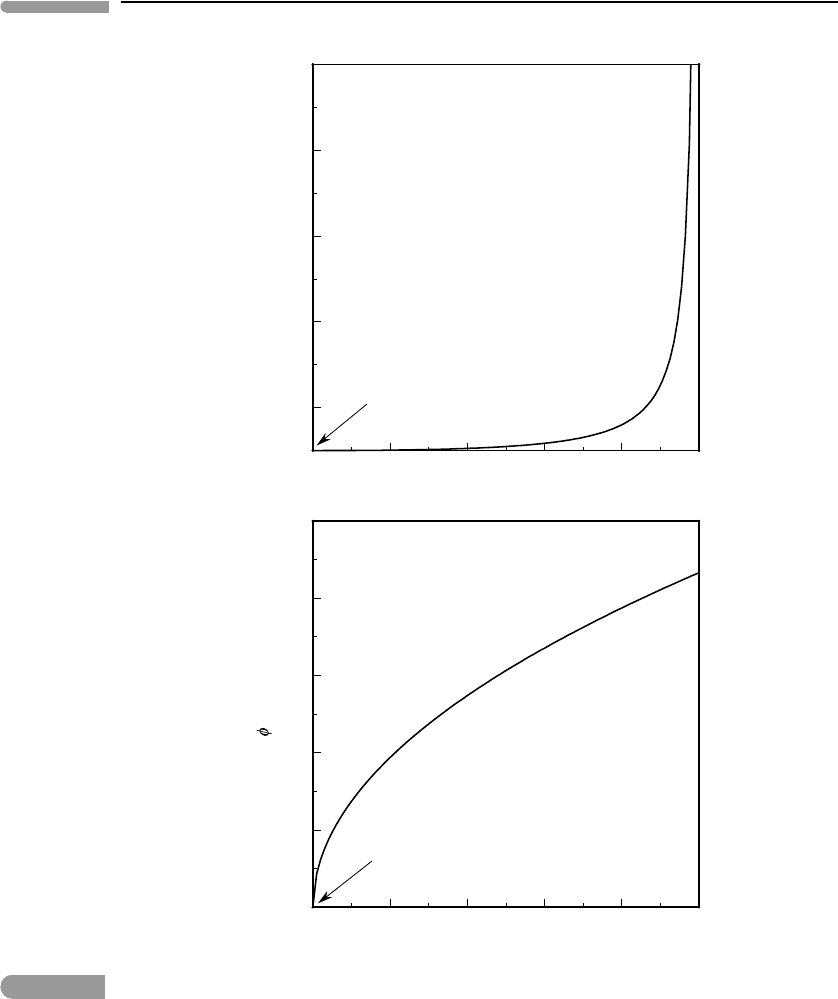
at the transition temperature. Figure 7.12 shows the ratio T

and the value of the order

parameter at the transition temperature T

, as a function of (−g

). The tricritical phase

transition occurs at (−g

) = 0. As this ratio increases, T

initially stays infinitesimally

close to T

, but the order parameter at T

increases rapidly. It is apparent that discriminating

experimentally between a tricritical phase transition and one that is first order but associated

with a small discontinuity may not always be easy.

7.6.4 Some comments of Landau theory

Landau theory is empirical and provides only an approximate description of actual phase

transitions. Still, it is a powerful analytical tool to understand the nature of phase transitions,

and in some instances, such as order–disorder transformations in minerals, it does an excel-

lent job of describing the thermodynamic functions associated with these transformations.

It is also very flexible – in the preceding section we have barely scratched the surface of

what Landau theory is capable of, and although space constraints prevent us from digging

deeper into it, there are a couple of points that are worth exploring in some more detail.

First, what is the physical significance of the α and g

parameters? We begin by noting

that α has units of entropy, and g

and g

have units of energy. We now re-write (7.47), or

(7.54), as follows:

−αT

=0. (7.68)

We can interpret (7.68) as meaning that, if the phase transition took place as a first-order

transition at T

, then α would be the entropy of transition, and g

would be the enthalpy of

380 Critical phase transitions

0 0.2 0.4 0.6 0.8 1

-(g

)

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

-(g

)

taT

tricritical phase transition

Fig. 7.12

Values of the temperature and order parameter at a discontinuous phase transition, as a function of the ratio between

the Landau parameters g

and g

.Asg

→0 the temperature of the phase transition approaches the critical

temperature, and the transition becomes smoother. The phase transition is tricritical at g

=0.

transition. The phase transition is, however, either critical (7.47) or tricritical (7.54) and in

such cases α and g

may represent the total entropy and total enthalpy associated with the

phase transition, “spread out” from absolute zero (φ =1) to the critical temperature (φ =0).

In the case of a discontinuous phase transition we can manipulate (7.65) to show that α

381 7.6 Landau theory of phase transitions

represents the entropy of the phase transition at T

, and that the enthalpy of transition is a

non-linear function of g

and g

, although the individual meanings of g

and g

are obscure

(Exercise 7.8).

Second, what if we wish to look at the effect of some other intensive variable on the phase

transition? This is done by including additional terms in the Landau polynomial expansion.

Say that the intensive variable that we are interested in is Z. The simplest case is to add

only a quadratic term in Z, so that (7.42) (with g

substituted as in (7.44)) becomes:

(

)



T −T

c,0



Zφ

. (7.69)

The coefficient α

corresponds to the conjugate variable of Z, so that the product α

Z has

the dimension of energy (recall that α represents entropy, which is the conjugate variable of

T). The intensive variables that we are most commonly interested in are either pressure, in

which case the coefficient is labeled α

and represents a volume change associated with the

phase transition, or composition, in which case we will have α

terms representing chemical

potential changes.

By choosing to use only the quadratic term in Z we are coupling α

to α only. This means

that the value of α will be the same for any value of Z, but the g

s will vary with Z. I have

also addeda0tothesubscript of T

, to emphasize that this is the critical temperature at

a zero value of Z, i.e. setting Z = 0in(7.69) recovers (7.42). We now re-write (7.69)as

follows:

(

)



T −



c,0

−



(7.70)

and we define the critical temperature at Z, T

c,Z

as follows:

c,Z

≡



c,0

−



. (7.71)

Substituting (7.71)in(7.70) we get an equation in T and φ only, which is identical to (7.42)

(with g

substituted as in (7.44)). This makes all the other equations valid, except that the

numerical values of the critical temperature and of the g

parameters will be different from

those obtained with Z = 0. From (7.71) we also get the value of critical Z at T

c,Z



c,0

−T

c, Z



. (7.72)

Note that, in contrast to T

, there is no a priori requirement that the disordered phase be stable

on any particular side of Z

. This depends on the sign of α

, which is not predetermined

as in the case of α (by equation (7.44)). For instance, if α

is negative then the critical

temperature increases with increasing Z, and the supercritical (disordered) phase is stable

on the low Z side of the phase transition (see also Box 7.1).

Worked Example 7.2 Lambda phase transitions and phase equilibrium

Several important rock-forming minerals undergo lambda phase transitions which arise

from a variety of microscopic processes. We already mentioned the case of perovskites,

in which crystal symmetry changes occur with increasing temperature. More subtle

symmetry changes are observed in quartz (transition between α quartz and β quartz at 847

K and 1 bar) and in carbonate minerals.Albite and anorthite display full Si–Al disorder above

critical temperatures (at 1 bar) of 950 K and 2300 K, respectively, and progressive ordering

382 Critical phase transitions

below those temperatures. Iron and nickel oxides, as well as the respective metals, undergo

order-disorder phase transitions associated with the orientation of magnetic moments. The

energetic effects of these phase transitions must be incorporated in the calculation of phase

equilibrium. The data set of Holland and Powell (1998 and electronic updates, henceforward

HP98) includes lambda phase transition properties that have been regressed simultaneously

with standard state properties, so that they are mutually consistent (see Worked Example 5.7

for a refresher of why internal consistency of thermodynamic data is important). Holland

and Powell find that the energetic effects of lambda transitions for all minerals in their data

base can be accurately modeled by means of a tricritical Landau potential (equation (7.53)),

regardless of the microscopic nature of the transformation in each particular mineral. The

equations in Section 7.6.2 are applicable to their data, with two important caveats. First,

HP98 reverse the sign of S(φ) in equation (7.57). Second, they use 298 K as the reference

point for Landau potentials (i.e. they make G(φ) = 0 at 298 K). The effect of these changes

is that the maximum value of entropy, at T

, is a positive number rather than zero. With

their convention S(φ) is in fact always positive, and would become zero at 0 K (compare

equations (7.57)).

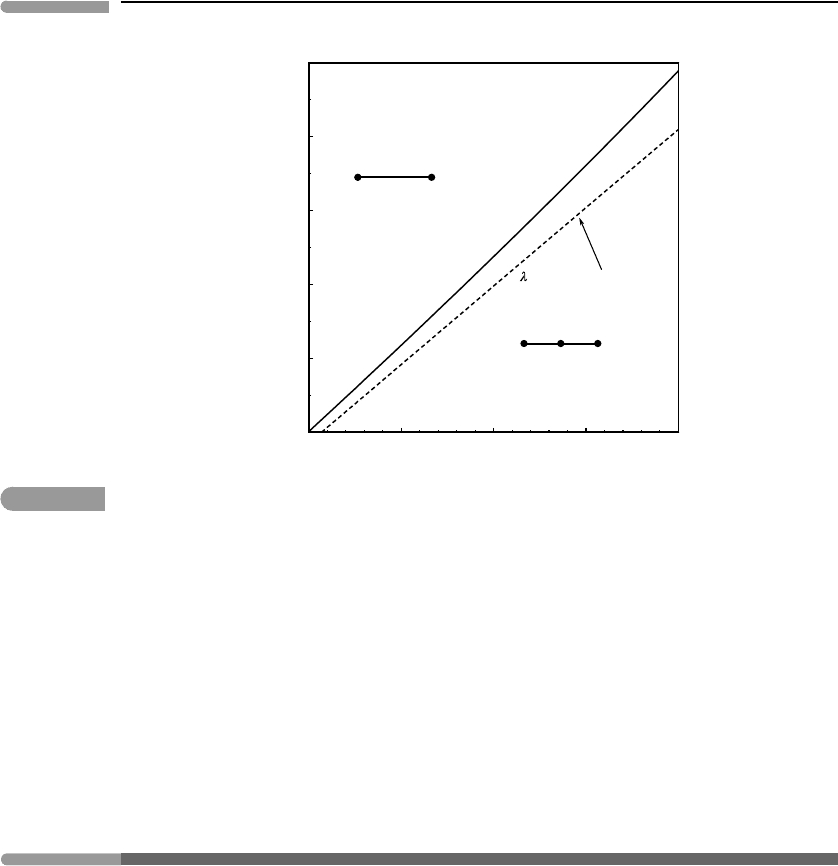
Figure 7.13 shows the Landau potentials for several minerals, calculated from HP98

(see Software Box 7.2). The effect of their sign convention is to make the diagrams

look like Fig. 7.6 (bottom). As in that case, I also show the Landau potential of the

metastable disordered phase below T

for one mineral (ilmenite) to emphasize that what

really matters is the Gibbs free energy change that accompanies the ordering process, i.e.

500 1000 1500 200

–5

–4

–3

–2

–1

Temperature (K)

G( ) (kJ mol

–1

)

ilmenite

disordered ilmenite

(metastable)

magnetite

hematite

albite

quartz

G of ordering

Fig. 7.13 Gibbs free energy of ordering, G(φ), also called the Landau potential, for several minerals, calculated with data

from Holland and Powell (1998). The lambda phase transition for each mineral occurs at the end of the respective

curve. Holland and Powell change the convention from G(φ)=0 for the disordered phase (e.g. Figs. 7.6, 7.10 and

7.11) to G(φ) = 0 at 298.15 K, for consistency with the way in which chemical thermodynamic calculations are

usually done. The value of G of ordering is not affected: compare the example of ilmenite, for which G of the

metastable disordered phase is shown with a broken line, with Fig. 7.6 and its rotated equivalent, Fig. 7.11.

383 7.6 Landau theory of phase transitions

the distance between the stable and metastable curves. Restoring Landau’s sign and refer-

ence conventions rotates the curves as in Fig. 7.11, but the distance between them remains

invariant. The figure shows that lambda phase transitions in minerals cause free energy

changes of the order of a few kilojoules per mol, which are not insignificant values (see

Section 5.2.1).

Software Box 7.2. Incorporation of the Landau potential to Gibbs free energy of minerals

A procedure is included in worksheet th_shomate.mw that calculates the Gibbs free

energy of order–disorder transitions in minerals, with the formalism of Holland and

Powell (1998). The name of the procedure is landau_hp. It calculates the Landau

potential of a mineral at any given P and T, using tabulated values of T

max

and V

max

as defined by Holland and Powell (1998). Recall that their sign convention is different

from the one commonly used in physics, but procedure landau_hp takes care of this.

Since the procedure is encapsulated in the package th_shomate.mw it can be called

from any other worksheet.

The strategy to include the Landau potential in mineral equilibrium calculations is

to call landau_hp for each of the species that participates in a reaction, multiply by

the corresponding stoichiometric coefficient, and add up all of the Landau potentials

(they may be zero for some species). The result is added to the Gibbs free energy of

reaction as an “excess term”. Worksheet th_template_4.mw contains a procedure

named Gord that does this. The solution for the equilibrium position must now be

found iteratively, because there is a conditional statement in landau_hp that checks

whether the temperature is above or below the lambda phase transition. This conditional

statement is not accepted by Maple’s equation solver fsolve. The way around this

problem is illustrated in procedures Peq and Teq, that solve for pressure at given

temperature, and for temperature at given pressure. The procedures first find a tentative

solution assuming that the sum of Landau potentials is zero. They then calculate the

Landau potential sum at this pressure and temperature, solve again including this interim

Landau potential, and so on, iterating until consecutive solutions converge within a

desired interval (set at 1 bar or 1 K). Peq is able to solve for pressure directly, but Teq

asks for an initial temperature guess, needed because of the non-linearity of the heat

capacity equations. If needed, the procedures can easily be incorporated in a loop to

calculate a phase boundary, as in th_template_3.mw (e.g. Figure 7.14; exercise

left to the reader).

Procedures Peq and Teq also include a call to vdp, which is another procedure,

included in the package th_shomate.mw, that calculates the pressure integral in

equation (5.1.7) with Holland and Powell’s compressibilty and thermal expansion data.

This is discussed in Chapter 8.

An example of the effect of lambda phase transitions on calculated phase equilibrium is

shown in Fig. 7.14. The breakdown of albite to jadeite plus quartz is an important indica-

tor of the transition between medium pressure metamorphism (greenschist–amphibolite

facies) and high-pressure metamorphism (blueschist–eclogite facies). Both albite and

384 Critical phase transitions

400 500 600 700 80

Temperature(°C)

Pressure (kbar)

NaAlSi

SiO

NaAlSi

SiO

Jd Qtz

Jd QtzAb

transitions in qtz and ab

ignored

Fig. 7.14

Effect of ignoring G of ordering in albite and quartz on the calculated position of the breakdown reaction of

albite to jadeite +quartz.

quartz undergo lambda phase transitions. The figure shows the location of the univari-

ant phase boundary calculated with and without the energetic contributions of these

phase transitions. Ignoring the Landau potentials displaces the calculated equilibrium

position by about 1 kbar. Note that, because albite and quartz are on opposite sides

of the reaction, the contributions from the two minerals cancel each other to some

extent. The effect would be greater if only one of the phases underwent a lambda phase

transition.

Exercises for Chapter 7

7.1 Convert the diagrams on the left of Fig. 7.1 from G

mixing

to G

solution

, and show that

the two points with a common tangent in the subcritical region are no longer minima,

but they still have a common tangent.

7.2 Derive the conditions (7.43) for a critical phase transition.

7.3 Show that equation (7.45) generates curves like those in Fig. 7.7. (Use any good

scientific plotting program.)

7.4 Find the equation for H (φ) for a system that undergoes a critical phase transition. Show

that spontaneous ordering must be exothermic. Assume that the system that undergoes

spontaneous ordering is contained in a larger isolated system. Discuss how the entropy

of this isolated system changes during ordering.

7.5 Prove that, if g

=0, then φ must be given by (7.52).

7.6 Show that (7.53) generates a family of curves with the same general characteristics as

(7.45), but with sharper curvature. (Use any good scientific plotting program.)

385 Exercises for Chapter 7

7.7 Explain why, if the second equation in (7.63) is the equilibrium equation, it must be valid

for φ = 0 for all T < T

. Show that the non-zero solution of this equation corresponds

to the positive square root of the quadratic equation, and derive equation (7.67) for the

order parameter.

7.8 Show that for a first-order phase transition α represents the entropy of the phase

transition at T

, and derive an equation for the enthalpy of the phase transition.

Equations of state for solids and the internal

structure of terrestrial planets

Inferring the internal structure of solid planetary bodies requires that we use thermodynamic

theory in order to interpolate and extrapolate often sparse experimental data to very high

pressures and temperatures. The constant-volume approximation that we used in Chapter 5

to calculate the Gibbs free energy of solids at high pressure leads to erroneous results at

depths greater than a few km. This situation is remedied by introducing a variety of equations

of state for condensed phases, that are accurate over progressively greater pressure ranges.

The study of equations of state for condensed phases that are valid at very high pressures and

temperatures will allow us not only to perform chemical equilibrium calculations relevant to

deep planetary interiors but also to predict physical conditions – pressure and temperature –

as a function of depth in solid planets.

8.1 An introduction to equations of state for solids

In Chapter 5 we calculated the following integral for solid phases assuming that their molar

volumes remain constant:



V(P,T)dP. (8.1)

This is tantamount to assuming that the second derivatives of the Gibbs free energy vanish

(equations (4.136) and (4.137)), which is in general not true. All materials change in volume

in response to changes in pressure and temperature, and a change in volume entails a

change in free energy. This energy needs to be accounted for, both when studying chemical

transformations (i.e. calculation of phase equilibria) and when inferring physical conditions

in planetary interiors. For example, equation (3.32) is a general differential equation for

the adiabat, based exclusively on thermodynamic relations and thus independent of specific

material properties. Integrating this equation so as to find the temperature distribution inside

a convective planet requires knowledge of how α, V and C

(all of which are derivatives

of the free energy) vary with temperature and pressure. Throughout Chapter 3 we assumed

that these properties are all constant, and although this may be fine as a first approximation

it introduces unacceptably large errors in detailed work.

Recall from Chapter 1 that the functional relationship between the three variables, P, V

and T, is called an equation of state (EOS). Operationally, the procedure to construct an EOS

begins with a reference value for the volume, which we symbolize V

. Except in surface and

near-surface environments, P ! 1 bar, so that the reference pressure is commonly taken to

be 0, and the reference volume is called the zero-pressure volume, even if it is customarily

386

387 8.1 An introduction to equations of state for solids

measured at 1 bar (1 ≈ 0, if P ! 1). The reference temperature, T

, may be taken either

at the standard reference temperature for thermodynamics (298.15 K), or at 0 K (in which

case we refer to the zero-temperature volume). The most appropriate choice depends on

the nature of the EOS, and when stating the value of V

=V(0,T

) I will always explicitly

state the value of T

We seek a function that yields either the volume at P and T ,V (P ,T ), which is called a

volume-explicit EOS, or the pressure at V and T, P(V ,T ), which is called a pressure-explicit

EOS.As with other thermodynamic calculations, we construct the function in steps, allowing

only one intensive variable to change at a time. Two different approaches are summarized

in Fig. 8.1. One possibility is to calculate the effect of isobaric thermal expansion at zero

pressure, from T

to the temperature of interest. This takes the volume from V

to V(0,T ). We

then hold the temperature constant and calculate the effect of compression to the pressure of

interest (labeled “hot isothermal compression” ), so that we obtain the volume at the P and T

of interest, V(P,T). Equations of state for materials at very high pressures and temperatures,

such as in deep planetary mantles and cores, are often constructed following the alternate

route shown in Fig. 8.1. In this approach we must consider separate contributions to pressure,

so that the total pressure, P, is given by:

P = P

. (8.2)

In this equation P

is the pressure required to change the volume from the reference volume

to the volume at the pressure and temperature of interest V(P,T), along an isothermal

compression path at the reference temperature, which is labeled “cold isothermal compres-

sion” in the figure. The pressure at the end of the cold isothermal compression leg, P

such that V(P

, T

) = V(P,T). This is the pressure associated with elastic compression

of the material at the reference temperature. Heating at constant volume (isochoric) from

to T generates additional pressure contributions. One of them, called thermal pressure,

, arises from increased vibrations of the atoms about their mean equilibrium positions

(see Section 1.14). The other term in (8.2), P

, arises from electron vibrations. It is negli-

gible in dielectric materials such as silicate rocks, but becomes important in metals at high

temperature (e.g., in the cores of terrestrial planets) and in plasmas (such as liquid metallic

hydrogen in the cores of giant planets). Unless otherwise stated we will assume that P

=0,

as in Fig. 8.1.

Both approaches to constructing an equation of state require that we find a functional

relationship between pressure and volume at constant temperature (to handle the isother-

mal legs in Fig. 8.1). Such a function is known as an isothermal EOS. In the following

sections we discuss three different ways of constructing isothermal EOS: from thermody-

namics (Murnaghan EOS), from finite strain (Birch–Murnaghan EOS) and from interatomic

potentials (Born–Mie EOS). The first two are macroscopic approaches and the resulting

isothermal EOS are applicable at any temperature, as long as the material properties at

the temperature of interest are known. Isothermal EOS based on interatomic potentials, in

contrast, incorporate a microscopic model of the material and are rigorously correct only

at0K.

The two approaches summarized in Fig. 8.1 differ substantially in the way they handle the

effect of temperature. In the “hot isothermal compression” method one adjusts the material

properties in the isothermal EOS to the temperature of interest (Section 8.2.2). In the “cold

isothermal compression” method a separate term is added, that accounts for thermal pressure

(Sections 8.3 and 8.4).