Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

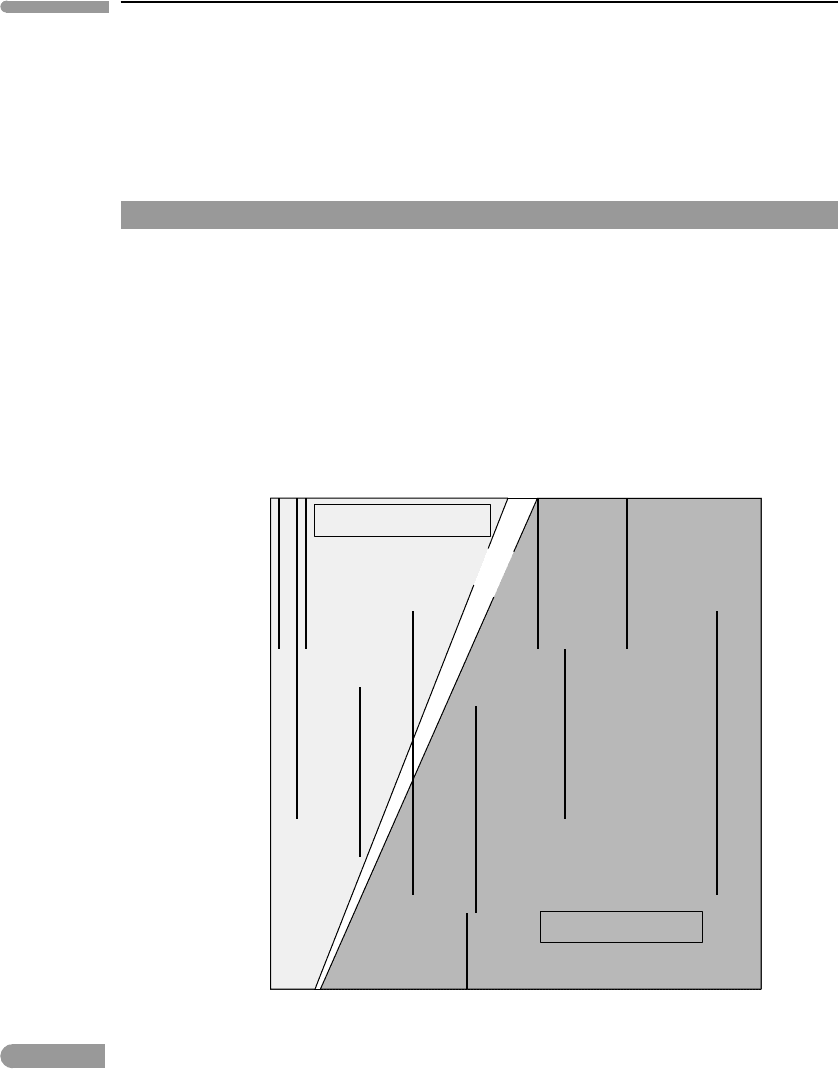
358 Critical phase transitions

kinetically unfavorable (Chapter 12). In either of these cases only the supercritical phase is

commonly found in natural assemblages.Agood example of this is olivine.Alternatively, the

critical temperature in strongly non-ideal solutions may be high enough that the supercritical

phase is suppressed by formation of a stable higher entropy phase, most commonly a melt.

Crystallization of two pyroxenes from basaltic melts is an example of this.

Worked Example 7.1 Rock-forming minerals as supercritical vs. subcritical phases

Despite the fact that equation (7.12) is only an approximate description of real solutions, it

does a reasonable job of explaining why some minerals display continuous solid solution

between two end-members, but others do not. This is summarized in Fig. 7.4. The two

diagonal lines in the figure show values of T

as a function of W

, calculated with equation

(7.12) and for two different values of τ

(0.89 and 1), corresponding to K

values of 0.5

and 1, respectively. These values span the range of possible values for these variables (see

Fig. 7.3).

In addition to calculated values of T

, the figure shows data for a number of rock-forming

minerals. The horizontal coordinate of each thick vertical line is an approximate value

0 1020304050

500

1000

1500

(kJ mol

–1

)

(K)

0.5

En - Fs

Prp - Al m

Phl - Eas

Fo - Fa

Or - Ab

Di - En

Ms - Pr

Cc - Mg

Prp - Grs

Hc - Mt

Or - An

subcritical solutions

supercritical solutions

Fig. 7.4 Miscibility relationships in some common rock-forming minerals. The diagonal lines labeled K

=1 and K

=0.5

map critical mixing temperature, T

as a function of W

(equations (7.12) and (7.13)). Solid solutions are plotted in

terms of approximate values of their largest interaction parameter (∼W

), and likely temperatures of formation in

rocks. En-Fs: orthopyroxene; Prp-Alm: Fe-Mg garnet; Fo-Fa: olivine; Phl-Eas: Mg-Al trioctahedral mica; Or-Ab: K-Na

feldspar; Cc-Mg: calcite–magnesite; Ms-Pr: K-Na: dioctahedral mica; Di-En: orthopyroxene–clinopyroxene; Prp-Grs:

Mg- Ca garnet; Hc-Mt: Al-Fe

ferroan spinel; Or-An: K-Ca feldspar.

359 7.3 Calculation of non-dimensional solvi

for the larger interaction parameter (W

) measured in each solid solution. The lengths of

the lines are very rough estimates of the characteristic temperature ranges in which the

minerals form, or at least exist stably. For example, olivine (Fo-Fa) and orthopyroxene (En-

Fs) are associated with igneous and solid-state mantle processes, for which characteristic

temperatures may be in the range 1200–1700 K. Given the small excess Gibbs free energy

of mixing in these minerals their critical mixing temperatures may be close to room tem-

perature, so that they always crystallize as supercritical phases. The same is true of Fe-Mg

garnets and Mg-Al micas. On the other hand, mixing between clino- and orthopyroxenes is

associated with much higher excess Gibbs free energy of mixing. We could say that two dis-

tinct subcritical phases (clino- and orthopyroxene) form even in high-temperature magmatic

systems, because the critical point for this solution is metastable relative to (discontinuous)

melting reactions. Pyroxenes are actually more complicated than this, undergoing other

types of discontinuous phase transitions in the solid state, but the description based on

critical mixing is probably correct in general terms, and physically appealing. Other exam-

ples of minerals that commonly occur as subcritical phases are K-rich–Ca-rich feldspars,

muscovite–paragonite and Mg and Ca carbonates in low-temperature near-surface envi-

ronments. Note that the critical temperature for calcite-magnesite mixing is ∼1000 K, so

that a supercritical Ca-Mg carbonate phase might crystallize from carbonatitic magmas.

The alkali feldspars are an interesting case in that they can crystallize (e.g. from granitic

magmas) as a single supercritical phase that often unmixes into two subcritical phases upon

cooling, generating perthitic intergrowths.

7.3 Calculation of non-dimensional solvi

The two branches of the solvus at any temperature T<T

are the two points X

(α) and

(β) that simultaneously satisfy the following two equations (see Fig. 7.1):



∂G

mixing

∂X



X=X

(

)



∂G

mixing

∂X



X=X

(

)

(7.14)

and:



G

mixing



X=X

(

)



G

mixing



X=X

(

)

[

(

)

−X

(

)

]



∂G

mixing

∂X



X=X

(

)

(7.15)

The first equation establishes the common tangent (equal chemical potentials in both

phases), the second one simply states that the difference in Gibbs free energy between

the two phases equals the slope of the common tangent times the difference between the

compositions of the phases at equilibrium. These equations are initially written in terms

of G

solution

, rather than G

mixing

, but all standard state properties drop out, resulting in

(7.14) and (7.15) (check this by yourself!). The equations express fundamental thermo-

dynamic relations that are independent of any particular model that one may choose to

describe the Gibbs free energy of mixing. They are thus general but, in order to solve them,

we must choose an explicit function to describe G

mixing

. As in the previous section we

will choose an asymmetric Margules function with no temperature dependency, with the

360 Critical phase transitions

understanding that we are doing this in order to investigate how solutions in general behave

in the subcritical region, and not as a rigorous and accurate description of any specific

system.

Since G

mixing

, or its first derivative, appear on both sides of equations (7.14) and (7.15)

we can divide throughout by RT and rewrite these equations in terms of the non-dimensional

parameter (G

mixing

/RT ). Introducing the non-dimensional parameters K

and τ defined

in the previous section we have, for an asymmetric Margules excess mixing function:

G

mixing

=X ln X +

(

1 −X

)

(

1 −X

)

(

1 −X

)

[

(

1 −X

)

]

(7.16)

and its first derivative:

∂

∂X



G

mixing



=ln X −ln

(

1 −X

)



(

−1

)

−2

(

−1

)

X +K



(7.17)

Substituting (7.16) and (7.17)in(7.14) and (7.15) we end up with two equations in the

two unknowns, X

(β) and X

(α), that can be solved in terms of K

and τ , for values of

τ<τ

. The task might be rather unpleasant by hand (I’m not sure it even has an analytical

solution) but Maple handles it without breaking a sweat (Software Box 7.1).

Software Box 7.1

Procedure solvi in worksheet solvus.mw solves the non-dimensional solvus spec-

ified by equations (7.14) through (7.17). The procedure uses Maple’s diff function

to calculate the first derivative of the Gibbs free energy equation (equation (7.17)), so

that even though it is written for an asymmetric Margules equation it should be possible

to substitute a different Gibbs free energy function and find the solvus for some other

description of the excess mixing function. Care must be exercised when specifying the

maximum temperature in the input line (parameter tauhigh), as if this value is higher

than τ

the procedure will crash. The procedure appears to be stable for tauhigh up

to ∼0.9999τ

The result of these calculations is a solvus that shows the compositions of the coexist-

ing subcritical phases as a function of the non-dimensional temperature τ . Four examples

are shown in Fig. 7.5, calculated for different values of K

. Recall that if G

excess

described with a temperature-independent Margules function then τ

and X

depend only on

(equations (7.11) and (7.13)). With increasing asymmetry the solvus becomes narrower

and “leans” in the direction of the component that generates the greatest amount of excess

Gibbs free energy of mixing. The effect is that the stability field of the subcritical phase rich

in the “more ideal” component becomes wider at the expense of the phase rich in the “less

ideal” component (we could have expected this to be the case on purely intuitive grounds).

A real solution with a given degree of asymmetry (given by the value of K

) will exhibit

a solvus with the same shape as the corresponding non-dimensional solvus, scaled in its

vertical coordinate according to the value of W

361 7.4 Order–disorder phase transitions

0 0.2 0.4 0.6 0.8 1

0.5

0.6

0.7

0.8

0.9

0 0.2 0.4 0.6 0.8 1

0.5

0.6

0.7

0.8

0.9

0 0.2 0.4 0.6 0.8 1

0.5

0.6

0.7

0.8

0.9

0 0.2 0.4 0.6 0.8 1

0.5

0.6

0.7

0.8

0.9

=0.5

= 0.6

= 0.89

= 0.64

=0.3

= 0.90

= 0.70

= 0.0

= 0.94

= 0.74

Fig. 7.5

Solvi for hypothetical solutions with temperature-independent interaction parameters, plotted in terms of

non-dimensional temperature, τ . In this simple case τ

, X

and the width and location of the solvus are determined

only by the asymmetry of the solution, given by the non-dimensional parameter K

7.4 Order–disorder phase transitions in crystalline solids

In the preceding sections we discussed critical phase transitions focusing on the example

of unmixing of a single-phase solution as its temperature drops below the critical mixing

temperature. Critical mixing is only one particular instance of a wide class of phenomena

that are governed by the same statistical mechanical principles, and that can be described

using the same theoretical framework. We will now begin to see what this means, although

our discussion of critical phenomena will not be complete until we discuss fluids, in Chapter

9. A note of caution: many algebraic manipulations in the remainder of this chapter have

362 Critical phase transitions

been omitted owing to space constraints. I believe that a full comprehension of the physics

involved requires a clear understanding of where the equations come from. I include some

of the important derivations as end-of-chapter problems, and others are left to the reader,

but I think that it is crucial that you fill in the gaps as you go over this material.

Minerals can undergo microscopic changes with temperature and pressure, such as

changes in their crystalline structures or in cation ordering, that have energy implications.

Such changes must be accounted for in order to have a full and accurate thermodynamic

description of a mineral at any temperature and pressure. In contrast to Sections 7.1 to

7.3, in this section we will restrict ourselves to transformations at constant composition. It

is important to understand that the changes that we are discussing here are distinct from

polymorphic transformations. The latter are first order phase transitions: they are step-

wise structural changes that take place “in full” at a specific temperature and pressure.

For instance, you can have either kyanite or sillimanite, but not something in between.

They are different minerals, with distinct crystalline structures, optical properties, densi-

ties, entropies, etc. Their Gibbs free energies are the same at the univariant phase boundary,

but their entropies and volumes (the first derivatives of G) are not. These discontinuities

in ∂G/∂T and ∂G/∂P are reflected in the enthalpy of transition, or latent heat, and are the

hallmark of discontinuous, or first order, phase transitions.

In critical phase transitions, which for historical reasons are also known as second-order

phase transitions, microscopic changes occur gradually over a finite temperature interval

and are completed at a well-defined temperature. For example, a mineral may display long-

range cation ordering (Worked Example 4.3) at low temperature and become progressively

disordered as the temperature increases, until its cation arrangement becomes fully random

at a well-defined transition temperature, known, for reasons that we shall presently see, as

the lambda temperature: T

. It then remains in the same state of complete disorder for all

temperatures higher than the lambda temperature, until the mineral’s demise at a first-order

phase transition. Order–disorder phase transitions are observed, for instance, in minerals in

which Si and Al occupy similar cation sites, such as feldspars and aluminosilicates. They

are also common in compound oxides, such as spinels and ilmenite, and in minerals of Fe

and other transition metals, in which they arise from the alignment of magnetic moments of

individual atoms. The lambda temperature is a critical temperature with the same properties

as those of the critical mixing temperature, the critical temperature of a fluid, or the Curie

temperature of a magnet, among many other examples.

Consider a crystalline structure in which there are two types of atoms that can exchange

places with one another in two types of crystallographic sites. These could be, for example,

Si and Al over different types of tetrahedral sites, or Fe atoms with oppositely pointing

magnetic moments over different octahedral sites. Our first task is to define a variable that

describes quantitatively the state of long-range order of the crystalline structure. Recall

from Chapter 4 that a structure with perfect long-range order is one that has maximum

information content, by which we mean that we are absolutely certain of what type of atom

we will find in each type of crystallographic site. For example, in microcline, which has

long-range order, the four T1a sites are occupied by Al, whereas the four T1b sites and the

eight T2 sites are occupied by Si. At the other extreme, in a perfectly random structure we

can only define the probability of finding a certain kind of atom in a certain kind of site.

This probability is equal to the fraction of atoms of the kind we are interested in, relative

to the total number of atoms that can enter the site. Thus, in sanidine, which has a fully

disordered structure, all we know is that we havea1in4probability of finding an Al atom,

anda3in4probability of finding a Si atom, in any one tetrahedral site.

363 7.4 Order–disorder phase transitions

Let us call the probability of finding atom X in site ξ, P

Xξ

. We define a parameter φ,

called the order parameter, as follows:

φ =

Xξ

−P

Xξ, random

Xξ, ordered

−P

Xξ, random

. (7.18)

Clearly, it must be 0 ≤φ ≤1, with φ =1 for the structure with perfect long-range order, and

φ = 0 for a structure with complete disorder, i.e. fully random. This formula is general, but

we will apply it to our example of two types of atoms, let us call them A and B, mixing over

two crystallographic sites, say α and β. For simplicity we will assume that the stoichiometry

and structure of the mineral are such that there are equal numbers of A and B atoms and

α and β sites. In principle the relative amounts of A and B could change, but here we are

only interested in changes in the crystal at constant composition, AB. We will define the

state of perfect long-range order as the one in which A atoms occupy only α sites, and B

atoms occupy only β sites. In the disordered state any site, α or β, has the same probability

of being occupied by A or B. We then have:

Aα, ordered

Bβ, ordered

Aα, random

Bβ, random

(7.19)

which, substituting in (7.18), yields:

φ =2P

Aα

−1 = 2P

Bβ

−1 (7.20)

or, equivalently, and, as we shall see, more usefully:

Aα

Bβ

(

1 +φ

)

Aβ

Bα

(

1 −φ

)

(7.21)

When A and B atoms redistribute themselves in the crystal there is a change in configu-

rational entropy. This change arises not only if A and B are atoms of different elements,

but also, for instance, if they are atoms of the same element (e.g. Fe) with differently ori-

ented magnetic moments. As long as the atoms are distinguishable there is entropy to pay

when we shift them around (Chapter 4). There is also an enthalpy cost, however, that arises

from the fact that the energetic interactions between the different types of atoms are not

necessarily equal. For example, if A and B are different atoms then the enthalpies of forma-

tion of A–A, B–B and A–B bonds may be different. In the case of alignment of magnetic

moments, energy is exchanged when the moments flip between parallel (A–A or B–B) and

anti-parallel (A–B) arrangements.

To deal with this we split-up the Gibbs free energy of the crystal as follows:

G =G

(

T , P

)

(

)

(

T , P

)

(

)

−TS

(

)

. (7.22)

In this equation G(T , P ) is a function of temperature and pressure (and perhaps composition,

but we keep that variable fixed in this case) but not of the state of order of the structure. The

free energy contribution that arises from the state of order of the structure, G(φ), consists of

an enthalpy term, H (φ), and a configurational entropy term, S(φ), which correspond to the

enthalpy and entropy effects that we described in the previous paragraph. For the crystal

364 Critical phase transitions

to be in homogeneous thermodynamic equilibrium at T and P the order parameter, φ, must

take the value that minimizes G(φ) at that T and P. Since G(T ,P ) is not a function of φ,

minimizing G(φ) assures that G is also minimized. In general, the value of φ that minimizes

G(φ) is a function of T (and P, although initially we will ignore the pressure dependency).

To see why, suppose that the enthalpies of formation of all bonds are negative, but that the

enthalpy of formation of A–B bonds is greater in absolute magnitude (more negative) than

those of A–A and B–B bonds. One might think naively that the stable configuration, i.e.

the one with lowest Gibbs free energy, would be the one that maximizes the number of

A–B bonds. Such a structure would, however, have perfect long-range order (φ = 1), and

its configurational entropy would vanish. Thus, and given that the enthalpy and entropy

contributions to G have opposite signs, maximizing the number of A–B bonds might not

minimize G(φ). Perhaps some value of φ<1 would produce enough configurational entropy

to more than compensate for the loss of someA–B bonds. Moreover, since S(φ) is multiplied

by T, the value of φ that minimizes G(φ) must be a function of temperature. The fact that

the Gibbs free energy of a system includes competing enthalpy and entropy contributions

is what allows it to undergo a critical phase transition.

In order to construct the function G(φ) we begin by finding explicit expressions for H (φ)

and S(φ). The latter is the configurational entropy that we learned to calculate in Chapter

4 (equation (4.55)). Say that in one mol of mineral (N sites) there are N /2 each of α and β

sites. The total number of microstates, O, equals the product of microstates for the α and β

sites, O

and O

(

N/2

)

(

Aα

)

(

Bα

)

(

N/2

)



Aβ





Bβ



(7.23)

Using Stirling’s approximation and the definitions of the site occupation probabilities, P

Xξ

we find after some simplification:

ln O

Aα



N/2

Aα



Bα



N/2

Bα



=−

(

N/2

)

Aα

ln P

Aα

−

(

N/2

)

Bα

ln P

Bα

(7.24)

and an identical expression for lnO

, substituting P

Bβ

and P

Aβ

for P

Aα

and P

Bα

, respectively.

Using (7.21) and simplifying some more we get:

ln O = ln O

+lnO

=N ln 2 −

(

N/2

)

[

(

1 +φ

)

(

1 +φ

)

(

1 −φ

)

(

1 −φ

)

]

(7.25)

finally arriving at:

(

)

=R ln2 −

[

(

1 +φ

)

(

1 +φ

)

(

1 −φ

)

(

1 −φ

)

]

. (7.26)

It is a good idea to check what (7.26) is saying. For the fully ordered state φ = 1 and

S(φ) =0 (recall that the limit of x ln x for x going to zero is 0), whereas for the fully random

state, φ =0 and S(φ) =R ln2.

Say now that the formation of each type of nearest-neighbor pair, A–A, B–B and A–B

is associated with an enthalpy ε

, ε

and ε

, respectively, and call the number of each

365 7.4 Order–disorder phase transitions

type of nearest-neighbor pairs ν

, ν

and ν

.Ifz is the coordination number of the

crystal, then:

·P

Aα

·P

Aβ



1 −φ



·P

Bα

·P

Bβ



1 −φ



(7.27)

·P

Aα

·P

Bβ

·P

Bα

·P

Aβ



1 +φ



The enthalpy of formation of all nearest-neighbor pairs in a mol of crystal is then given by:

+ν

(

+ε

+2ε

)

(

2ε

−ε

)

. (7.28)

Because the first term in the right-hand side of (7.28) is not a function of φ, we may consider

it to be part of G(T ,P ) in equation (7.22). We thus get:

(

)

(

2ε

−ε

)

(7.29)

or, defining:

η =

(

2ε

−ε

)

(7.30)

we re-write (7.29) as follows:

(

)

=ηφ

. (7.31)

The constant η is the difference between the enthalpy of formation of different nearest

neighbors and the enthalpy of formation of same nearest neighbors. Thus, η>0 means

that the formation of AB nearest neighbors is either less exothermic or more endothermic

than the formation of AA and BB nearest neighbors, or, in other words, that there is A–B

avoidance in the crystal. Conversely, η<0 implies that there is preference for the formation

of A–B nearest neighbors.

Collecting terms from (7.22), (7.26) and (7.31) we arrive at:

(

)

=ηφ

−RT ln 2 +

[

(

1 +φ

)

(

1 +φ

)

(

1 −φ

)

(

1 −φ

)

]

. (7.32)

We seek the value of φ that minimizes this function, so we equate its first derivative to zero:

(

)

dφ

=2ηφ +



1 +φ

1 −φ



=0 (7.33)

and note that φ = 0 is always a solution to this equation. But is this particular solution a

minimum, and is it the only solution? To answer these questions we begin with the second

derivative:

(

)

dφ

=2η +

(

1 −φ

)

. (7.34)

366 Critical phase transitions

We now see that, if η ≥ 0, then the second derivative at φ = 0 is always positive, meaning

that G(0) is in this case always a minimum. Moreover, if η ≥ 0 then φ = 0 is the only

solution to (7.16), as any non-zero solution requires:



1 +φ

1 −φ



≤0, (7.35)

which is impossible for φ>0. What this means is that, if there is either A–B avoidance

(η>0) or neither preference for nor avoidance of A–B nearest neighbors (η = 0) , then the

only stable configuration is the fully disordered state, except for the special case η = 0at

T =0, where φ could be greater than zero (and the Third Law says that, in a perfect crystal,

it must be 1). Note that, if η>0, then long-range order is not even possible at absolute zero.

We could have arrived at these conclusions by simple inspection of (7.22). They are also

what one should expect on physical grounds: the only way of spontaneously overcoming

disorder is if there is an energetic advantage for formation of A–B pairs, which is not the

case if there is A–B avoidance.

The case η ≥ 0 is, then, rather uninteresting, as there is no possibility for the system to

undergo a phase transition. Again on physical grounds, we should expect this not to be the

case for η<0, as in this instance A–B affinity may cause the structure to become ordered

at some finite temperature. We now note that, although φ = 0 is a solution to (7.33) with

η<0, it is not necessarily a minimum. In order for this solution to be a minimum it must be:

2η +RT > 0 (7.36)

or:

T>−

2η

. (7.37)

Thus, the fully disordered structure is the stable one (lowest Gibbs free energy) for

temperatures greater than the lambda temperature, T

, given by:

=−

2η

. (7.38)

Before we continue, note that this equation for T

is formally identical to the one for the

critical mixing temperature of a solution: setting τ =1in(7.12), we get T

/2R. This

is no coincidence, as we shall see.

For T<T

the solution φ =0 is a maximum, so we need to find whether there is another

solution to (7.33) that minimizes G(φ). We rewrite (7.33) as follows:



1 +φ

1 −φ



=−

2η

φ =

φ, (7.39)

which, making use of the rather obscure hyperbolic trigonometric identity:

tanh

−1

x =



1 +x

1 −x



(7.40)

367 7.4 Order–disorder phase transitions

becomes:

tanh

−1

. (7.41)

Equation (7.41) has non-zero roots over the domain of tanh

−1

φ, which is |φ|< 1, so we are

assured that for every possible value of the order parameter, G(φ) will have an extremum

at some temperature T<T

. Moreover, since the solution φ = 0 is a maximum and G is a

continuous function, the other solution 0 <φ<1 must be a minimum.

Figure 7.6 (top) shows φ vs. T/T

, calculated with (7.41). If we start from a disordered

phase (φ = 0) at high temperature (T>T

) we see that, as the temperature is lowered,

ordering begins at T =T

, and φ initially increases very rapidly with decreasing temperature

below T

. The value of the order parameter is very close to 1 at T ∼ 0.5T

, and changes

very little with further cooling to T = 0. Figure 7.6 (bottom) shows dimensionless Gibbs

free energy: G(φ)/RT

(substitute (7.38)in(7.22)), plotted as a function of dimensionless

temperature, T/T

. As we saw, for T>T

there is only one possible value of G(φ),

that corresponds to φ = 0. G(φ) has two possible values below T

, a maximum at φ = 0

(shown with a dashed line in Fig. 7.6 (bottom)) and a minimum at the value of φ>0

given by Fig. 7.6 (top) (shown with the solid curve in 7.6 (bottom)). The disordered phase

becomes metastable below T

relative to a phase with some degree of long-range order,

which increases with decreasing temperature. In nature the disordered high-temperature

phase may persist metastably below T

, depending on the nature of the cooling process, but

that is a different story (Chapter 12). The shape of the function G(φ) for various values of

temperature is shown in Fig. 7.7, plotted as non-dimensional values normalized to G(0):

−[(G(φ) −G(0))/G(0)]. Indeed, for T>T

the minimum occurs at φ = 0, whereas for

T<T

the function goes through a maximum at φ = 0 (corresponding to points on the

dashed curve in Fig. 7.6 (bottom)) and a minimum at φ>0 (points on the solid curve in

Fig. 7.6 (bottom)). The distance between the maximum and minimum (i.e. between the

two curves in Fig. 7.6 (bottom)) increases with decreasing temperature. Note that at T =T

the function has a very “flat” minimum, reflecting the fact that the second derivative vanishes

(substitute (7.38)in(7.34)), and so does the third derivative (check for yourself). The fourth

derivative is positive, though, ensuring that φ = 0 is a minimum at T

. The attentive reader

will have noticed that this is the same behavior that we found at the critical mixing point

(see Section 7.1, and especially Fig. 7.1).

Examining Fig. 7.6 (bottom) we see that G(φ) is not smooth at T

, meaning that its

derivatives are discontinuous. The phase transition that occurs at the lambda temperature,

called a lambda phase transition is, however, continuous, in the sense that there is no

entropy “jump” at the transition. If the lambda phase transition is continuous then the shape

of G(φ) in Fig. 7.6 (bottom) is a problem, as it would imply that there are discontinuities in

entropy and volume, which characterize first-order phase transitions. Clearly something is

missing from our description of the lambda phase transition. This problem, together with

the realization that there are phase transitions that at first sight have no obvious relationship

to order–disorder transformations yet behave in the same fundamental way, led to the

development of a mathematical formalism to describe phase transitions known as Landau

theory, named after the great mid twentieth-century Russian physicist Lev Landau. As we

shall see, one of the fundamental insights that comes out of Landau theory is the realization

that transitional behavior between continuous and discontinuous phase transitions is also

possible.