Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

368 Critical phase transitions

0 0.2 0.4 0.6 0.8 1 1.2

0.2

0.4

0.6

0.8

0 0.2 0.4 0.6 0.8 1 1.

–0.8

–0.6

–0.4

–0.2

T/T

G(φ)/RT

G(0)

ordered phase stable

disordered

phase stable

(a)

(b)

G(φ)

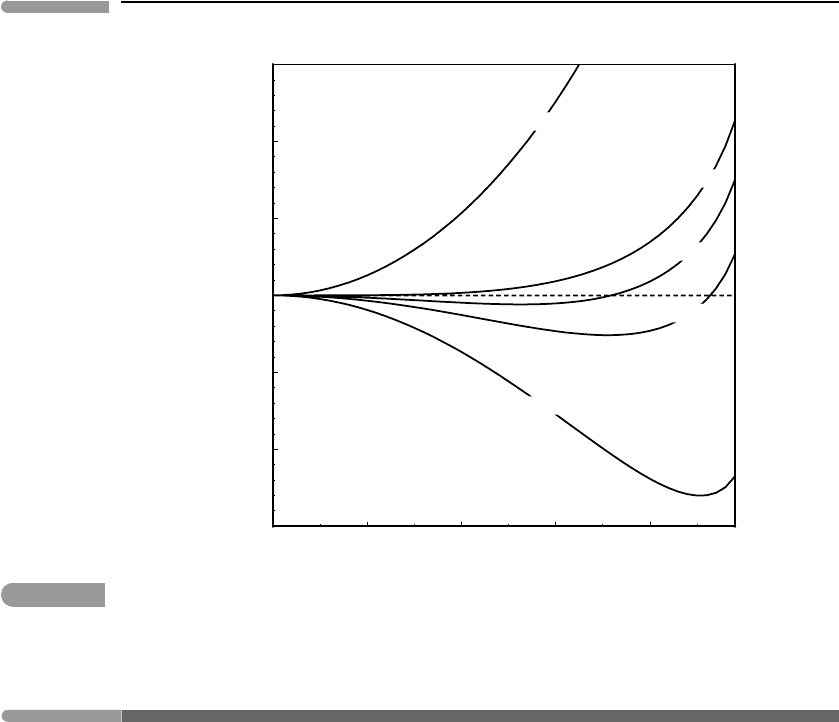
Fig. 7.6

(Top) Order parameter vs. non-dimensional temperature for a phase in which two types of atoms, A and B, occupy

two crystallographic sites, α and β, such that X

and that there is A–B afﬁnity. (Bottom)

Ordering contribution to the Gibbs free energy of the phase, shown in non-dimensional units. G(0) is the Gibbs free

energy of the disordered phase, which for T < T

is metastable relative to the ordered phase, shown by G(φ).

369 7.5 Analogies with other phase transitions

0.2 0.4 0.6 0.8

–0.3

–0.2

–0.1

0.1

0.2

0.3

T/T

=10

-(G(φ) - G(0))/G(0)

T/T

=0.6

T/T

=0.8

T/T

=0.9

T/T

Fig. 7.7

G(φ) as a function of φ at constant temperature. The value of φ at each minimum corresponds to the value of φ at

that temperature in Fig. 7.6, with φ = 0 for T ≥ T

7.5 Analogies with other phase transitions

There are systems that display behaviors that are remarkably similar to order–disorder

phase transitions, even though at first sight they do not appear to bear close similarities

to the atomic ordering processes that we discussed in the previous section. The key is to

identify a variable in the system that can serve as an order parameter. Figure 7.8 shows

some examples. The top panel is a calculated lambda phase transition for atomic ordering

– it is in fact the same curve as in Fig 7.6 (top), scaled so as to make comparisons with

the other examples easier. The second panel shows the difference in composition between

the two branches of a calculated symmetric solvus (e.g. from Figs. 7.1 or 7.5), plotted

against the ratio T/T

, where T

is the critical mixing temperature. The vertical coordinate

is X

(α) −X

(β). This variable takes values between 0 and 1 (see Fig. 7.1) and it can serve

as the order parameter. The curve is identical to that in the top panel, but note that the two

curves describe different phenomena. In one case it is atomic ordering in a single phase at

constant composition. In the other it is separation of two phases of different composition

from a single homogeneous supercritical phase. A way to think of this is as “ordering” of

the components A and B into the phases α and β, with perfect order (pure A and pure B)

attained only at T = 0, but already approached very closely at ∼0.5T

(see Fig. 7.5).

Some minerals acquire higher symmetry with increasing temperature. For example, a

mineral may be orthorhombic at low temperature but, owing to anisotropic thermal expan-

sion, the lengths of its a and b crystallographic axes become progressively closer to one

370 Critical phase transitions

0.5 0.6 0.7 0.8 0.9 1

0.2

0.4

0.6

0.8

NaMgF

perovskite

unit cell dimensions

Zhao et al., 1993

symmetric solvus

(calculated)

O liquid–vapor

phase transition

lambda transition

(calculated)

0.5 0.6 0.7 0.8 0.9 1

0.2

0.4

0.6

0.8

( X-)

( )

0.8 0.85 0.9 0.95 1

0.2

0.4

0.6

0.8

T/T

(

ropav

iuqil d

ropav

0.4 0.6 0.8 1

0.05

0.1

-b(aA)

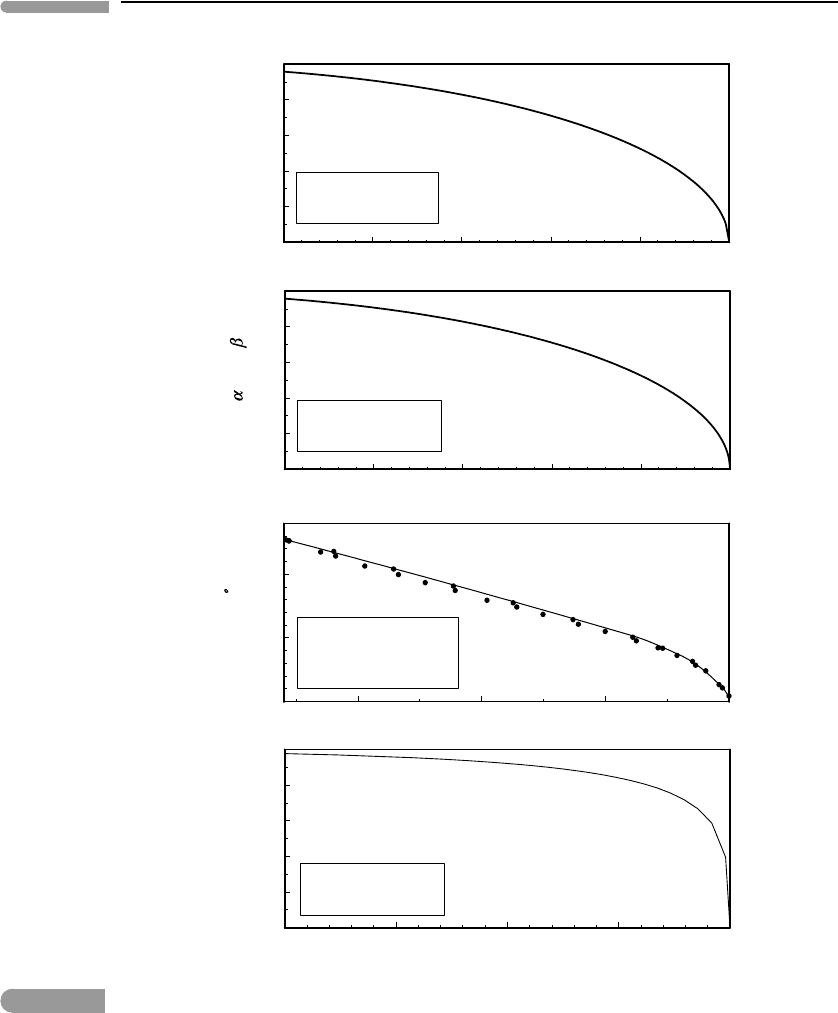
Fig. 7.8

Order parameter vs. non-dimensional temperature. Measured values of crystallographic axes of NaMgF

perovskite

from Zhao et al. (1993). The other three curves are calculated and correspond to: the hypothetical phase in Figs. 7.6

and 7.7, the symmetric solvus in Fig. 7.1, and liquid–vapor equilibrium in H

O (Chapter 9).

another with increasing temperature, until at a well-defined temperature a and b become

equal. When this happens the symmetry changes from orthorhombic to tetragonal. It can

also happen that all three axes become equal at a single temperature, and in such case the

symmetry of the crystal changes from orthorhombic to cubic. The third panel in Fig. 7.8

371 7.5 Analogies with other phase transitions

shows data for a solid, NaMgF

with perovskite structure, that behaves in this way. It

is orthorhombic at low temperature, but as temperature increases the lengths of its three

crystallographic axes approach each other and the solid undergoes a lambda-type phase

transition at T

≈ 1050 K, where it takes on cubic symmetry. The figure shows the dif-

ference (in Å) between the lengths of the a and b crystallographic axes (data from Zhao

et al., 1993). This difference serves as the order parameter, and could be converted, if one

wishes, to a non-dimensional variable that takes the value 1 at T = 0 by dividing by a −b

at 0 K. Even without doing this, however, the figure shows clearly that a −b goes to 0 at an

accelerating rate as T

is approached, just as in the case of an order–disorder transition. In

fact, the change in crystal symmetry can be understood as an order–disorder transition by

considering rotations and distortions in the crystalline framework that affect the entropy of

the crystal (see, for example, Putnis, 1992).

The bottom panel in Fig. 7.8 shows the difference between the molar volumes of water

vapor and liquid water coexisting at equilibrium (obviously, pressure cannot be constant

along this curve – why?), normalized to the volume of the vapor. The molar volumes

become equal at the critical temperature (∼647.3 K) and a single supercritical phase exists

at T>T

. Two phases exist below T

, and their volumes diverge rapidly immediately below

this temperature. We shall return to critical phenomena in fluids in Chapter 9. There are

other important critical phenomena that we will not discuss in this book. Examples include:

the para-ferromagnetic transition at the Curie temperature, responsible, for example, for

the preservation of thermal remanent magnetization in igneous rocks; the appearance of

superconductivity in some materials at low temperature; and the existence of a superfluid

liquid-helium phase near absolute zero. What is common to all of these processes is that in

all of them it is possible to define an order parameter that goes to zero continuously and at

an accelerating rate as the critical temperature is approached from below, and that stays at

zero above the critical temperature.

It has been known for a long time that systems that behave in this way display anomalies

in the second derivatives of the Gibbs free energy in the neighborhood of the critical

temperature. This is true of heat capacity, compressibility and thermal expansion (equations

(4.135)to(4.137)), but for now we will focus on c

only. At a first-order phase transition

these three quantities become infinite, because as long as a univariant assemblage is present

energy transfer (either thermal or mechanical) causes changes in entropy and volume at

constant temperature and pressure, by forming some phases at the expense of others. The

“infinite heat capacity” occurs only at the first order phase transition, at which S and V are

discontinuous, but c

(and the other second derivatives) behave normally everywhere else.

At a lambda phase transition the second derivatives are anomalous in the neighborhood of

the transition temperature, and diverge strongly (but may or may not become infinite) at the

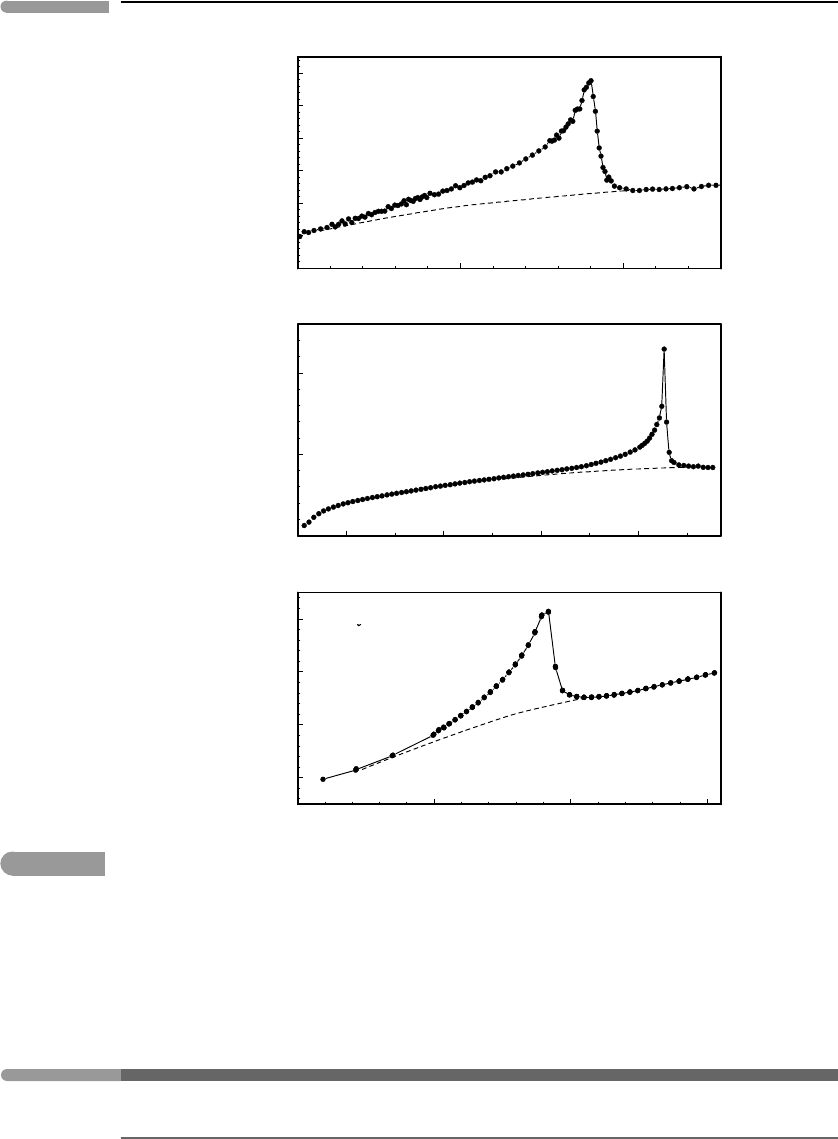
transition temperature itself. Three examples of this behavior are shown in Fig. 7.9. The top

two correspond to crystal symmetry phase transitions, including the example of NaMgF

perovskite. The bottom panel in Fig. 7.9 corresponds to an order–disorder transition caused

by alignment of magnetic moments in ferrosilite. In every case the dashed curve shows what

the “normal” heat capacity would be expected to be. The measured values define a strong

and steep positive anomaly relative to these expected values, which is characteristically

lambda-shaped, hence the name for this type of phase transition. An important point is that,

whether or not c

becomes infinite at the transition temperature, the function is integrable

across the transition, i.e., the area under the lambda-shaped anomaly is finite. This area needs

to be known in order to be able to calculate the entropy of the solid at T > T

(Section 4.7.1).

372 Critical phase transitions

350 400 450

210

220

230

240

250

260

270

T (K)

20 30 40 50

T (K)

400 600 800 1000

100

150

200

T (K)

J(K

–1

lom

–1

)

J(K

–1

lom

–1

)

J(K

–1

lom

–1

)

ZrW

Yamamura et al. (2004)

Ferrosilite (Fe

)

Cemic and Dachs (2006)

NaMgF

perovskite

Topor et al. (1997)

Fig. 7.9

Lambda heat capacity anomalies in three different solid phases. Data from references shown in the ﬁgure.

In the simple thermodynamic description of an order–disorder phase transition that we

developed in Section 7.4 there is no indication of the behavior depicted in Fig. 7.9. There

is need for a theoretical framework that reproduces this observed behavior.

7.6 Landau theory of phase transitions

7.6.1 Critical phase transitions

The key idea of Landau theory of phase transitions is to start with equation (7.22), in which

we made G equal to the sum of a function of T and P and a function of φ, and expand the

373 7.6 Landau theory of phase transitions

function G(φ) as a power series in φ. When this is done G(φ) is (informally) called the

Landau potential. As before, we seek the values of φ that minimize G(φ), but in this case

we will make no assumptions about the functional forms of H(φ) or S(φ). Rather, we will

derive these, as well as the heat capacity, from the temperature derivatives of the Landau

potential. We require that the order parameter be a non-dimensional variable in the interval

0 ≤ φ ≤ 1 and symmetric relative to 0, so that if we wish to define the order parameter

backwards it would be G(−φ) = G(φ) (this is a minor point, but simplifies the notation).

We also require that at a critical phase transition φ goes to zero as the critical temperature

is approached from below, and remains at zero for T > T

. Beyond these constraints we

attach no specific meaning to the order parameter, which gives us flexibility to define it a

posteriori in the most convenient way for each specific application. In fact, the requirement

that the maximum value of φ be 1 can be relaxed trivially, as we shall see.

Symmetry of the order parameter means that we must include only even powers of φ,so

that, including numerical coefficients that will simplify the derivatives, we write the power

series as follows:

(

)

+··· (7.42)

The coefficients g

are empirical macroscopic parameters, as is the order parameter φ. The

microscopic description that we used to construct (7.32) (number of microstates, energy

of nearest neighbor pairs), or any other kind of a priori microscopic model, is not a part

of Landau theory. Landau theory is an example of a mean field theory. The power of this

approach is that it is applicable to a large class of phenomena which may have only remote

microscopic similarities, and for which our microscopic understanding may be limited. Of

course, there is a drawback too, and that is that it provides little insight about the microscopic

nature of a specific phase transition.

We will initially assume that we can truncate the power series after the second term. As

usual, we require that there be a minimum of G(φ) for φ = 0atT ≥ T

, and for a value of

φ>0atT < T

. Taking the first and second derivatives of (7.42), these conditions require

the following three relationships (see Exercise 7.2):

> 0, T>T

< 0, T<T

=−

> 0, T<T

(7.43)

One solution to (7.43) is to make g

a positive constant, and g

a linear function of (T −T

=α

(

T −T

)

(7.44)

with α>0. We then re-write (7.42) as follows:

(

)

(

T −T

)

, α>0, g

> 0. (7.45)

This function has the same geometric properties as the function G(φ) plotted in Fig. 7.7:a

sharp minimum at φ = 0 for T > T

, a “flat” minimum for T = T

and a minimum at φ>0

and maximum at φ = 0 for T < T

(Exercise 7.3). Perhaps more interestingly, from the last

line in (7.43) we get an equation for φ valid for T<T

(we will use only the positive root,

374 Critical phase transitions

because by construction φ is symmetric):

φ =



(

−T

)



1/2

. (7.46)

If we scale the order parameter so that φ = 1atT = 0, then we get:

(7.47)

and:

φ =



1 −



1/2

. (7.48)

Note that scaling the order parameter to the interval [0,1] is a matter of convenience, not of

necessity. Function (7.48) is plotted in Fig. 7.10 (labeled “critical”). Substituting (7.48)in

(7.45), and recalling that φ = 0 for T ≥ T

we get:

(

)

=0, T ≥ T

(

)

=−



1 −



, T<T

(7.49)

0 0.5 1

0.2

0.4

0.6

0.8

T/T

critical

tricritical

first order

jump

Fig. 7.10

Order parameter vs. non-dimensional temperature predicted by Landau theory for three types of phase transitions.

The critical phase transition corresponds to the curve in Fig. 7.6 (top), but the curve in that ﬁgure was calculated from

a microscopic model of the phase, and the curve in this ﬁgure from mean-ﬁeld Landau theory. The tricritical phase

transition is associated with a lambda-shaped heat capacity anomaly, see Fig. 7.11. The ﬁrst-order phase transition

occurs discontinuously at T

375 7.6 Landau theory of phase transitions

and, differentiating (7.49) relative to T:

(

)

=0, T ≥ T

(

)

=−



1 −



=−

, T<T

. (7.50)

We note that at φ =0 both G(φ) and S(φ) are continuous, and G(φ) is smooth, confirming

that these equations describe a continuous, and not a first-order,phase transition. Calculation

of H (φ) is left as an exercise (Exercise 7.3). Note that spontaneous ordering is always

exothermic, so that the entropy of the “universe” increases by a greater amount than the

decrease in the entropy of the system given by (7.50), as required by The second Law (more

on this in Chapter 14).

We will label the contribution of the ordering process to heat capacity C

(φ) and, by

analogy with (7.22), we make C

= C

(P , T)+C

(φ). Differentiating (7.50) and using

(4.135):

(

)

=0, T ≥ T

(

)

=−

T , T<T

. (7.51)

Heat capacity is thus discontinuous at the phase transition, and this is in fact the origin

of the name “second order” – entropy (and volume) are not smooth across a continuous

phase transition, and the second derivatives of the free energy are thus discontinuous. The

name is discouraged, though, because in some cases discontinuities show up in higher

order derivatives. “Critical” or “continuous” are preferable names to encompass all “not

first order” phase transitions.

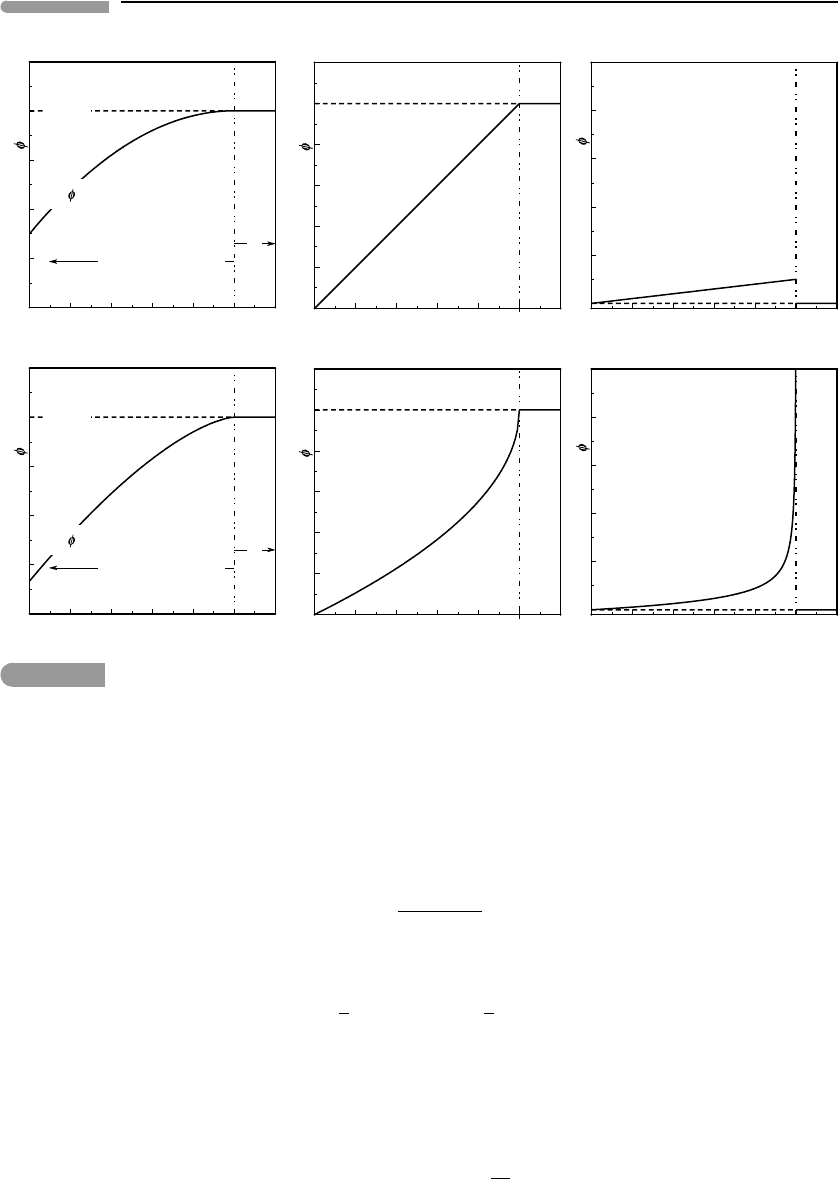
The behaviors of the three thermodynamic functions at a critical phase transition are

shown in the top three panels of Fig. 7.11. Comparison of the free energy plot with that in

Figure 7.6 (bottom) shows what Landau theory accomplishes: it makes G smooth across

the phase transition, while preserving the general relationship between G of the stable

ordered phase and G of the metastable disordered phase below T

. If you rotate the curves

to the left of the phase transition in Fig. 7.6 (bottom) counterclockwise until the dashed line

(G of metastable disordered phase) becomes the extension of the solid line (G of the ordered

phase above T

) you will get, more or less, the Gibbs free energy diagram in Fig. 7.11.

With this transformation G becomes smooth and S becomes continuous at the phase

transition.

7.6.2 Lambda phase transitions

Although heat capacity is discontinuous at T

, the ordering contribution to C

varies linearly

with temperature at T<T

(Fig. 7.11). Thus, although equations (7.45) through (7.51) are

a correct description of a continuous (or critical) phase transition, they do not describe

the behavior observed at lambda phase transitions, where C

characteristically diverges

strongly (Fig. 7.9). Can Landau theory be made to account for this? Inspection of equations

(7.51) suggests that, if g

were made a function of (T −T

), then the heat capacity function

would diverge as T → T

. However, it would not have a finite integral, so this solution

is not acceptable. We then do the next best thing, which is to make g

= 0, immediately

invalidating (7.45) through (7.51). We note, however, that if g

vanishes, then the only way

376 Critical phase transitions

–0.8

–0.4

G( )

–0.8

–0.4

S( )

( )

–0.8

–0.4

T/T

G( )

–0.8

–0.4

S( )

( )

G(0)

G( )

ordered phase stable

disordered phase stable

G(0)

G( )

ordered phase stable

disordered phase stable

Fig. 7.11

Gibbs free energy, entropy and heat capacity for systems that undergo a critical phase transition (top) or a tricritical

phase transition (bottom). The Gibbs free energy diagrams are similar to the one in Fig. 7.6 (bottom), rotated

counterclockwise so that the Gibbs free energy function is smooth. The effect of this rotation is to make entropy

continuous, but not smooth, at the phase transition.

of allowing for the ordered phase to be stable at T<T

is to have g

=0. In effect, we keep

(7.44) and the first two lines in (7.43), and from the first derivative of (7.42) with g

= 0

we replace the third line with (see Exercise 7.5):

(

−T

)

> 0, T<T

, (7.52)

which shows that it must be g

> 0. We then replace (7.45) with:

(

)

(

T −T

)

, α>0, g

> 0 (7.53)

and note that this function generates a family of curves that have the same general char-

acteristics as those obtained from (7.45) (Exercise 7.6). We now obtain a set of equations

that parallel (7.46) through (7.51), but with a crucial difference, as we shall see. Scaling the

order parameter as before so that φ = 1atT = 0, we have:

(7.54)

377 7.6 Landau theory of phase transitions

and, from (7.52):

φ =



1 −



1/4

, T<T

. (7.55)

Function (7.55) is labeled “tricritical” in Figure 7.10 (the reason for this name is essentially

historical, and need not concern us; see, for example, Griffiths & Wheeler, 1970; Griffiths,

1973). The Landau potential is now given by:

(

)

=0, T ≥ T

(

)

=−



1 −



3/2

, T<T

(7.56)

and the contribution of order–disorder to entropy:

(

)

=0, T ≥ T

(

)

=−



1 −



1/2

=−

, T<T

. (7.57)

The crucial difference is in the contribution of ordering to heat capacity, which now becomes:

(

)

=0, T ≥ T

(

)

√

(

−T

)

−1/2

, T<T

. (7.58)

The bottom panels of Fig. 7.11 show plots of the thermodynamic functions for tricritical

phase transitions (equations (7.56), (7.57) and (7.58)). The heat capacity diverges at T

but it has a finite integral. Comparison of (7.58) with measured heat capacities (Fig. 7.9)

suggests that a Landau potential given by (7.53) may provide a good approximation to the

behavior of solids that undergo lambda phase transitions.

7.6.3 Discontinuous phase transitions

Beyond the intriguing name, what is a tricritical phase transition? The difference with a

critical phase transition becomes clear once we realize that Landau theory can also describe

discontinuous phase transitions. We have considered the cases g

> 0 and g

= 0, so it is

natural to be curious about the case g

< 0. Let us begin by seeking the equilibrium value

of the Landau potential (with g

< 0) at the critical temperature. Taking the first derivative

of (7.42) and equating to zero:

(

)

dφ

=α

(

T −T

)

φ +g

=0 (7.59)

we find that at T = T

the Landau potential has extrema at φ = 0 and φ = (−g

)

–

recall that we only use the positive square root. The first non-vanishing derivative for the

solution φ = 0 is the fourth derivative:

(

)

dφ

=6g

< 0. (7.60)