Douce A.P. Thermodynamics of the Earth and Planets

Подождите немного. Документ загружается.

348 Phase equilibrium and phase diagrams

6.7 Consider the phases forsterite–enstatite–magnesite–vapor (of composition CO

)–

melt (of composition MgCO

) in the ternary system MgO–SiO

–CO

. Construct

a schematic phase diagram and use it to discuss the generation of carbonatite melts

in magnesite-free mantle peridotites. Is it possible, in this simple system, for a Mg-

carbonatite melt to crystallize a silicate mineral assemblage, leaving no traces of the

existence of a carbonate liquid?

6.8 Consider the four-component system MgO–CaO–SiO

–CO

, and the phases

forsterite, diopside, enstatite, calcite, vapor (of composition CO

) and melt (of com-

position CaCO

). Construct a schematic phase diagram for this system, and connect

it to the phase diagram in Fig. 6.11 via the multiply-degenerate reaction (di, fo, en,

v). Discuss the similarities and differences between this phase diagram, the one in

Exercise 6.7, and the one in Fig. 6.11.

6.9 Construct a schematic P–µ

phase diagram for ferroslite–fayalite–magnetite, at con-

stant temperature and µ

SiO

. Discuss the implications of your phase diagram for

the effects of pressure and oxidation conditions on the generation of tholeiitic vs.

calc-alkaline igneous differentiation trends.

6.10 Construct schematic T–µ

and P–µ

phase diagrams in the neighborhood of the

wustite (FeO)–cohenite (Fe

C)–metallic Fe–graphite invariant point in the ternary

system Fe–C–O. Use your diagrams to discuss whether there is more than one possible

explanation for the fact that metallic iron ± cohenite is more characteristic of the

interiors of small planetary bodies (e.g. asteroids and the Moon) than of large bodies

(e.g. Earth, Mars).

6.11 Construct P–T, P–µ

, T–µ

and µ

SiO

–µ

phase diagrams showing equilib-

ria among the phases: metallic iron, fayalite, schreibersite (Fe

P), whitlockite

(Ca

(PO

)

), perovskite and ilmenite, in the six-component system Fe–Si–P–Ca–

Ti–O. Discuss the various pathways by which whitlockite microcrystals can exsolve

from metal grains in chondritic meteorites.

6.12 In Worked Example 6.9 I calculated a methane–ethane melting loop under the assump-

tion that the two ices are fully miscible. This may not be the case. The opposite

“end-member” possibility is that they are perfectly immiscible, and that the ice mix-

ture exhibits eutectic behavior. Calculate the phase diagram that results from this

assumption, using the Maple worksheet described in Software Box 6.1 (all necessary

data are given in Worked Example 6.9). How does this affect the conclusions about

the possible nature of Titan’s surface hydrocarbons?

6.13 Refine the calculation of Triton’s atmospheric composition by calculating the pressure

and composition of the vapor in equilibrium with the four ices: N

, CO, CO

and CH

All the necessary data can be obtained from Lodders and Fegley (1998), Table 1.20.

Critical phase transitions

The phase transitions that we discussed in Section 6.6 are all discontinuous phase transitions.

They are step-wise changes in the structure of matter, for instance, the destruction of the

crystalline structure during melting or sublimation, or the breakdown of molecular bonds

in a liquid during boiling. These are microscopic changes that are accompanied by a macro-

scopic exchange of heat with the environment, what we call the enthalpy of transition

(melting, vaporization, etc.), or also “latent heat”. There is another type of phase tran-

sition, which takes place without there being a discontinuity either in the microscopic

structure of a substance or in its macroscopic properties, and during which there is no

energy exchange with the environment. Such phase transitions are called continuous or crit-

ical phase transitions, and play important roles in many planetary processes. For example,

they underlie exsolution phenomena such as are observed in feldspars, pyroxenes, oxides

and meteoritic metal, hydrogen–helium unmixing in fluid planets and liquid immiscibility

phenomena in magmatic systems. They also explain order–disorder transformations in crys-

talline substances. Critical phase transitions also play an important role in the study of fluids

(Chapter 9).

7.1 An intuitive approach to critical phase transitions

Consider a binary solution between components A and B with unit site multiplicity. If we

use X for the mol fraction of component A then the mol fraction of B is 1 − X, and the

Gibbs free energy of ideal mixing is given by equation (5.93):

G

ideal

mixing

=RT

[

X ln X +

(

1 −X

)

(

1 −X

)

]

. (7.1)

This function vanishes at X =0 and X =1, is negative everywhere in between, and becomes

more negative with increasing temperature. What this means is that, if two substances mix

ideally, then the solution (microscopic mixture) is always stable relative to a mechanical

(macroscopic) mixture of the pure substances, and becomes more stable (the tendency to

form the solution becomes stronger) with increasing temperature. The curve that represents

G

ideal

mixing

has a minimum and is concave up, as shown in Fig. 5.9. The second derivative

of (7.1) must therefore be everywhere positive, which you can verify by differentiating the

function. Let us now assume that the solution is not ideal. From (5.122):

G

mixing

=G

ideal

mixing

excess

. (7.2)

We begin by considering a hypothetical non-ideal solution that can be described with a

symmetric excess Gibbs free energy function (equation (5.146)) that is neither a function of

temperature nor of pressure (i.e. W

= W

= 0). This is the simplest possible description

349

350 Critical phase transitions

of a non-ideal solution. G

excess

vanishes at X = 0 and X = 1 and is positive everywhere in

between and independent of temperature. Because G

excess

and G

ideal

mixing

have opposite signs

and G

excess

is a function of composition only whereas G

ideal

mixing

is a function of both compo-

sition and temperature, the relative magnitudes of the two functions, and hence of G

mixing

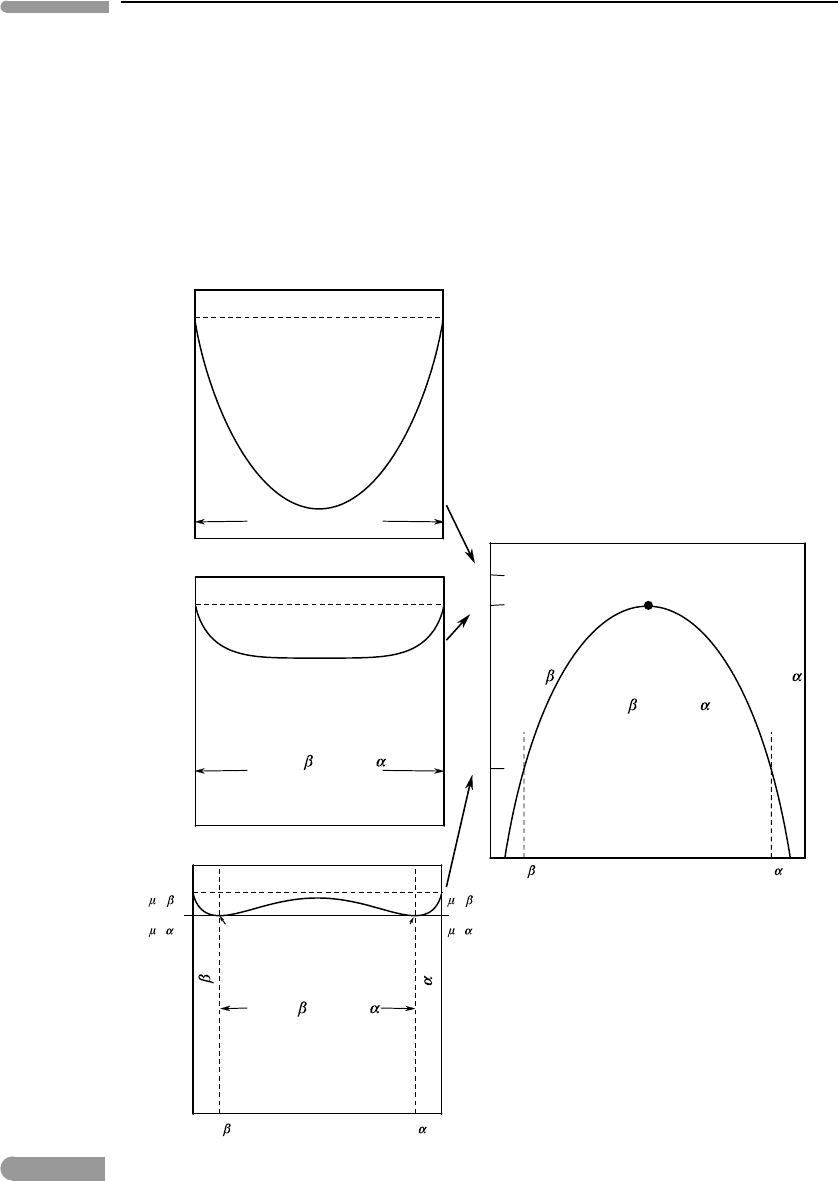
vary in interesting ways with temperature and composition. This is shown in Fig. 7.1.

At some high temperature T

the excess function is small enough relative to the ideal

function that G

mixing

has the properties of the ideal function, in particular, it is always

negative and concave up. This case corresponds to the top diagram on the left of Fig. 7.1.

∆G

mixing

∆G

mixing

∆G

mixing

phase phase

supercritical phase

( )

phase + phase

( )

( )X

( )

critical mixing point:

)

phase + phase

phase

supercritical phase

( )

phase = phase

= supercritical phase

Fig. 7.1

Gibbs free energy of mixing curves curves (left) for a symmetric non-ideal solution at the critical mixing temperature,

, and at a higher and a lower temperature. The curve on the T–X diagram (right) is the solvus. See text.

351 7.1 An intuitive approach

Under these conditions any composition between pure A and pure B forms a stable solution,

just as in the case of ideal mixing. As temperature decreases, however, G

ideal

mixing

becomes

less negative but G

excess

remains unchanged (and positive). The properties of the two

functions are such that at some temperature T

, G

mixing

takes the shape shown in the

bottom left diagram of Fig. 7.1 (see also Figure 5.13.c). At this temperature the curvature of

the G

mixing

function changes sign twice: there is a central interval with negative curvature

separated from two positively-curved intervals by two inflection points. Given a curve with

this shape it is possible to find two points, labeled a and b in the figure, which have a

common tangent. Note that in Fig. 7.1 these points happen to be minima, but this is only

because we are plotting Gibbs free energy of mixing, so that the vertical coordinate of

the two end-members is the same. A plot of Gibbs free energy of the solution would not

show these points as minima, but they would still have a common tangent. The common

tangent is what matters, for it means that there are two compositions in which each of the

components, A and B, have chemical potentials that are simultaneously the same (see also

Fig. 5.9). These compositions are labeled X

(β) and X

(α) in Figure 7.1. It is evident from

the figure that the Gibbs free energy of any solution that could form in between these two

compositions is greater than the Gibbs free energy of a macroscopic mixture of solutions

with compositions X

(β) and X

(α). Such a solution is therefore unstable relative to a

macroscopic mixture of phases with compositions X

(β) and X

(α).

Two distinct phases, which I have labeled phase α and phase β, are therefore stable at T

For any bulk composition in the interval X

(β)–X

(α) the stable assemblage consists of

two phases: phase β of composition X

(β) and phase α of composition X

(α). Two phases

in a binary system constitute a divariant assemblage, and since we have chosen arbitrary

values of pressure and temperature the compositions of the two phases are fixed. The stable

assemblage for bulk composition between X

(β) and X = 0 (pure B) consists of phase β

only. This can be seen from the fact (Figure 7.1) that any solution within this interval has

lower Gibbs free energy than a macroscopic mixture of pure B and X

(β). The one-phase

assemblage is trivariant, so that the composition of phase β if it exists at equilibrium by itself

is not fixed, but is rather given by the bulk composition of the system. Identical arguments

show that phase α alone is stable from X

(α)toX = 1 (pure A), and that its composition

within this interval equals the bulk composition of the system.

The two points X

(β) and X

(α) are compositions of phases that coexist at equilibrium.

They correspond to two points on a curve that maps compositions of coexisting phases as

a function of temperature, as shown on the right-hand side diagram of Fig. 7.1. This curve

is called a solvus and is the phase diagram for this system. Bulk compositions inside the

solvus consist of two phases at equilibrium, of compositions given by the two intersections

of the temperature coordinate with the solvus. Bulk compositions outside the solvus consist

of a single phase, of composition equal to the bulk composition. We will get to a formal

justification for the shape of the solvus below, but it should be intuitively apparent that the

solvus of the system that we are considering must become wider as temperature decreases

and the positive contribution of the excess term in (7.2) becomes greater in relative terms.

It is important to realize that the only thing that changed between T

and T

is temperature.

The nature of the phase has not changed, as reflected in the fact that the mathematical

description of mixing has not changed. The ideal and non-ideal contributions to Gibbs

free energy of mixing are described by the same equations and using the same values

for the interaction parameters throughout, and we have also implicitly assumed that the

standard state Gibbs free energies always refer to the same two end-members (otherwise

leveling G

mixing

at zero at the end-members for all temperatures would not be valid). The

352 Critical phase transitions

corollary follows that a solvus can exist only between condensed phases that have the same

or very similar microscopic structures, such that complete miscibility is possible at some

temperature. Examples include: two feldspars, two pyroxenes, two micas, two metals, two

liquids, etc. (but obviously not two gases, since gases are always fully miscible).

A temperature must exist at which the nature of the system changes from one in which

there is only one phase spanning the entire compositional range between A and B, such

as at T

, to one in which there is a compositional interval within which two phases are

stable, such as at T

. This temperature is called the critical temperature. The two branches

of the solvus converge on the same composition, X

, at the critical temperature, defining

the critical mixing point (X

, T

), see Fig. 7.1. This point is also called the consolute point,

but I prefer critical mixing point because it highlights the deep underlying analogies among

all critical phenomena, that we will explore further below and in Chapter 9.

But what exactly happens at the critical mixing point? If there are two distinct phases,

α and β, that can exist below the critical temperature, but only one above it, is the high-

temperature phase α or β, or something else altogether? The answers to these questions

begin with the middle diagram on the left-hand side of Fig. 7.1, which shows Gibbs free

energy of mixing at the critical temperature, T

. As we saw, for T < T

the Gibbs free energy

function has two inflection points, whereas for T > T

there are no inflection points. Recall

that at an inflection point the curvature of a function changes signs, and hence its second

derivative vanishes. We can move from T > T

to T < T

without any discontinuity, as

all that is entailed in doing so is changing the value of T, which is a continuous variable,

and monitoring how (7.2), which is a continuous function, responds. Somewhere along this

continuous path there must be a temperature – the critical temperature – at which the function

goes from having a second derivative that never vanishes to having a second derivative that

vanishes at two points. The only way in which this can happen without a discontinuity is

if at some temperature, which is the critical temperature, the second derivative vanishes

at one point only. Now, if the function vanishes at X = 0 and X = 1 and has a single

inflection point in between, then the sign of the curvature of the function cannot change at

this inflection point either. Mathematically this means that the third derivative of the Gibbs

free energy function vanishes as well. This special behavior is depicted in the middle left

diagram in Fig. 7.1. It corresponds to a curve that is very flat in the neighborhood of X

It is, if you wish, almost a straight line but not quite. Generally, the fourth derivative is

the lowest order derivative of the Gibbs free energy of mixing that does not vanish at the

critical point (Section 7.4).

Consider a phase of composition X

that forms at T > T

. We shall label any phase that is

stable at T>T

the supercritical phase. If the supercritical phase is cooled instantaneously

to a temperature T<T

it will have a finitely higher Gibbs free energy relative to a mixture

of phases α and β and this Gibbs free energy will act as a driving potential (see Section 5.3.2)

that will cause the single supercritical phase to unmix into a macroscopic mixture of the

subcritical phases α and β (albeit subject to kinetic constraints, Chapter 12). With an exper-

iment of this kind it would in principle be possible to distinguish between the supercritical

phase and the subcritical phases. However, if the final temperature of the experiment is made

progressively higher, all the while keeping it below T

, the driving potential for unmixing

becomes smaller (because the G

mixing

curve becomes flatter), and the compositions and

physical properties of the two subcritical phases become closer to one other, and also closer

to those of the supercritical phase. Finally, at T

it is no longer possible to distinguish

between the three phases. There is no discontinuous phase boundary between the supercrit-

ical phase and either of the two subcritical phases. Rather, at the critical point the system

353 7.1 An intuitive approach

changes continuously from a supercritical state in which only one phase is possible to a sub-

critical state in which two phases can exist at equilibrium. If the experiment is repeated with

a supercritical phase of composition other than X

then the phase will change continuously

and imperceptibly, as temperature is lowered, from the supercritical phase to either of the

two subcritical phases (depending on the bulk composition), until the temperature is reached

at which this particular bulk composition intersects the solvus and the other subcritical phase

will appear, in this case discontinuously. There is a direct analogy with the behavior of fluids:

the distinction between liquid and gas, and the discontinuous phase transition that separates

the two phases, vanishes continuously as the critical point is approached, and a single super-

critical fluid phase is stable above the critical temperature (Chapter 9). Application of the

phase rule at a critical point may be confusing, but it shouldn’t be (see Box 7.1).

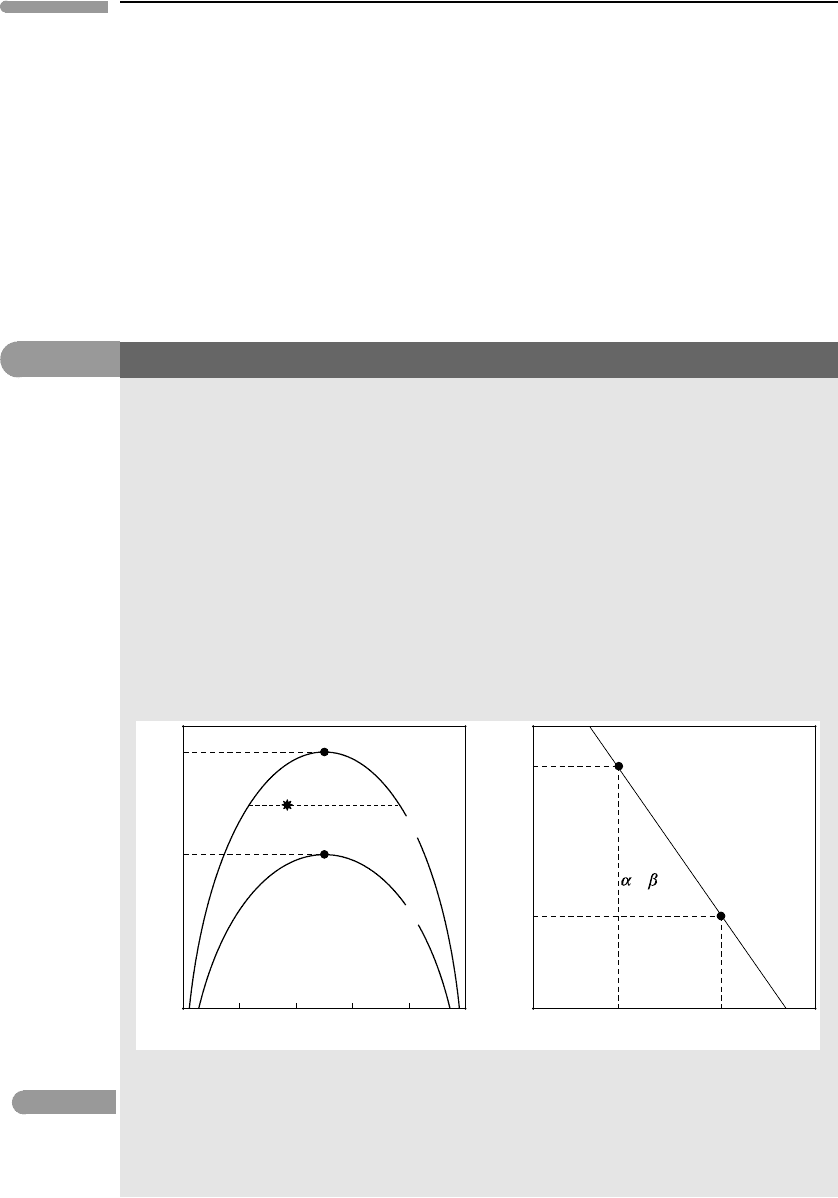
Box 7.1

The phase rule at a critical point

Consider a solvus in a binary system such as the one in the left-hand side panel of Fig. 7.2. The solvus is a

divariant phase boundary, as can be seen from an application of the phase rule. We have c =2, and along

the solvus the two phases, α and βs coexist at equilibrium, so F = 2 and f = 2. The solvus appears as

a one-dimensional curve, i.e. as a pseudo-univariant phase boundary, because we hold pressure constant,

thus “using up” one of the two degrees of freedom. At a different pressure the solvus will generally be

located at a different temperature. This is shown schematically by the two curves in the left-hand panel

of Fig. 7.2, where I have arbitrarily chosen the higher temperature solvus to correspond to a pressure, P

lower than that of the lower temperature solvus, P

. It could also be the other way around, but this diagram

is applicable, for example, to the system liquid molecular helium–liquid metallic hydrogen (see Fig. 2.16).

The solvus is also a ﬁrst-order phase transition. Consider bulk composition X

, at temperature T

and

pressure P

. At these conditions the system consists of the two phases, α and β, of compositions given

by the intersection of the temperature coordinate with the two branches of the solvus. If we change the

)

supercritical

phase

Fig. 7.2 Two solvus curves for a hypothetical system (left) in which the critical mixing temperature varies inversely with

pressure. The P–T curve on the right-hand side diagram maps the location of the critical mixing point. It is not a

univariant phase boundary, because only one phase is stable along the curve. Following Ricci (1966) we can call it a

“singular curve” that separates supercritical conditions (to the right) from subcritical conditions (to the left).

354 Critical phase transitions

Box 7.1

Continued

temperature while holding the pressure constant one of the phases will form at the expense of the other,

and the two phases will change composition. If we raise the temperature then phase α will eventually

disappear when the vertical coordinate X

intersects the solvus. These changes are “ﬁrst order” because there

is a difference in entropy and volume between the two phases, so that there is a non-vanishing enthalpy of

reaction associated with the phase changes.

More generally, this non-zero enthalpy change that characterizes ﬁrst-order phase transitions is what

makes it possible for invariant (and univariant, divariant, and so on) assemblages to exist in the ﬁrst place.

We can add or remove heat to an invariant system (e.g. an equilibrium assemblage of the three Al

SiO

polymorphs) and the system will stay at the P and T of the invariant point by forming some of the phases at

the expense of the others, until one or more of the phases disappears and the variance of the assemblage

increases. With two degrees of freedom rather than zero, this is what happens along the solvus.

Except at the critical point. Critical points have unique coordinates. Thus, in the two component system

shown in Fig. 7.2, the critical point at each pressure occurs at a unique temperature, which is thetemperature

at which coexistence of the two subcritical phases ends. We can show this by a curve in P–T space, as in the

right-hand panel of Fig. 7.2, that shows the combination of (T, P) coordinates at which the critical phase

transition takes place. The ﬁgure would appear to suggest that this curve is a univariant phase boundary

but

this is not correct

. By construction, the curve represents the P–T conditions at which phases α and β become

identical, and in effect identical to the supercritical phase. It is the locus of all critical points, two of which,

corresponding to the diagrams on the left, are shown in the ﬁgure.

Along the curve the system consists of a

one-phase assemblage

, so according to the phase rule it should be trivariant. Yet it shows as what looks like

a univariant phase boundary. Similarly, if one considers the critical point of a one-component ﬂuid (Chapter

9), this is the point at which the liquid–vapor equilibrium curve ends, and only one phase is present at the

critical point. It looks like an invariant point, but according to the phase rule its variance is 2.

What is going on here? Simply, that the variance is indeed what the phase rule says it should be. We will

see why in a moment but ﬁrst a note of caution. It is sometimes proposed that the way to ﬁx this conundrum

is by modifying the phase rule at the critical point, by subtracting a number of degrees of freedom equal to

the number of phases that become indistinguishable at the critical point (two in both the example of the

solvus and that of the ﬂuid critical point). The justiﬁcation offered for this is having to account for “conditions

of criticality”, and although it may work arithmetically, it is thermodynamically incorrect. The critical point

in a one-component system

is not invariant, and the P–T locus of critical mixing points in a two-component

system (Fig. 7.2)

is not univariant.

The correct description was formulated by Ricci a long time ago (Ricci, 1966, pages 24–27). He pointed

out that a critical point along a univariant phase boundary (e.g. the end of the liquid–vapor coexistence

curve, more on this in Chapter 9)isa

singular point: it is simply the point where the boundary ends. It is

not an invariant point, because exchange of even an inﬁnitesimal amount of energy will move the system away

from the critical point, which is distinctly different from what happens at a true invariant point.

Depending on

whether one adds (or subtracts) heat or work the system can move both in P and T, so the critical point is

indeed divariant. The fact that it is a “point”, with unique coordinates, does not make it invariant!

Consider a mixture at its critical mixing point. An inﬁnitesimal exchange of heat, or of mechanical energy,

or of matter, will move the system away from the critical point in T, P and X, respectively. The critical

point is indeed trivariant. Following Ricci’s terminology, we can label the curve on the right-hand diagram

of Fig. 7.2 a

singular curve: it is the boundary of a two-dimensional divariant ﬁeld, that extends to the

left of the curve in the ﬁgure. The coexistence of α and β ends at the singular curve because the phases

355 7.2 Location of the critical mixing point

Box 7.1

Continued

become identical. We can also state a general rule as follows: a critical phase transition occurs along an

n-dimensional boundary of an (n +1) dimensional region, over which an assemblage of subcritical phases

coexist. The phases become identical at the n-dimensional critical boundary, and only a single supercritical

phase exists on the other side of it.

So what makes phase equilibrium at the critical point different? Simply, the fact that there is no latent

heat associated with critical (continuous) phase transitions. Because entropy and volume are continuous

across a critical phase transition, 

transition

H =0. It therefore becomes impossible to have, for example, an

invariant assemblage, as transfer of even an inﬁnitesimal amount of energy will change the temperature

and/or pressure. The phase rule, and the variance that it predicts, are intact and there is no need to invent

“conditions of criticality”.

I must emphasize that although I used a symmetric Margules-type function to exemplify

the concept of critical mixing (because it generates simple diagrams, such as in Fig. 7.1),

the behavior is general. It arises from the fact that, if the relative magnitudes of the ideal and

excess contributions to Gibbs free energy of mixing change with temperature, then a transi-

tion from a Gibbs free energy function with no inflection points to one with two inflection

points must happen at some temperature. At this critical temperature both the second and

third derivatives of G

mixing

must vanish, giving rise to a continuous phase transition.

Unmixing of a homogeneous supercritical phase into two or more subcritical phases

is an important process in nature. Common examples include exsolution in high-pressure

mantle phases (such as pyroxenes from majoritic garnets), Widmanstätten textures in iron

meteorites, metal–sulfide–silicate liquid immiscibility, condensation of a supercritical fluid

into a liquid and coexisting vapor, and immiscibility between liquid helium and liquid

metallic hydrogen in the interiors of some giant planets (Chapter 2).

7.2 Location of the critical mixing point

Finding the critical mixing point of a solution is the first step in determining its solvus.

From the preceding discussion it follows that at the critical mixing point the following two

conditions must be satisfied:

∂

G

mixing

∂X

∂

G

ideal

mixing

∂X

∂

excess

∂X

=0 (7.3)

and:

∂

G

mixing

∂X

∂

G

ideal

mixing

∂X

∂

excess

∂X

=0 (7.4)

which, substituting (7.1), yield:

∂

excess

∂X

=−

(

1 −X

)

(7.5)

356 Critical phase transitions

and:

∂

excess

∂X

=−

(

2X −1

)

(

1 −X

)

. (7.6)

Equations (7.5) and (7.6) are general (for solutions of site multiplicity one). They contain two

free parameters, X and T, which means that they can be solved for a unique pair of values that

satisfy both equations simultaneously. These are the coordinates of the critical mixing point.

In order to solve the equations, however, it is necessary to substitute an explicit expression

for the excess Gibbs free energy function. As an example we will assume that the excess

Gibbs free energy can be represented by the asymmetric Margules function (5.143), with no

temperature dependency. Without loss of generality we can choose to label the components

such that W

≥W

, and make X =X

. We also define the variable K

, as follows:

(7.7)

and note that it must be K

≤ 1, with K

= 1 corresponding to the symmetric function

(5.146). Substituting these definitions in (5.143), taking the second and third derivatives of

the resulting function, and substituting in (7.5)and (7.6) we obtain, after some simplification:

−

(

1 −X

)

[

(

6X −4

)

−6X +2

]

(7.8)

and:

−

(

2X −1

)

(

1 −X

)

=6W

(

−1

)

. (7.9)

Dividing (7.8)by(7.9) and simplifying some more we get:

2X −1

2X −3X

(

1 −K

)

−1

(7.10)

which is a quadratic equation in X :

(

1 −K

)

(

10K

−8

)

X +

(

1 −2K

)

=0. (7.11)

The physical solution of this equation is X

, the composition of the critical mixing point.

Equation (7.11) shows that the composition of the critical mixture depends only on the

relative values of the interaction parameters, and not on their absolute values. In particular,

for a symmetric solution K

=1 and X

=0.5, which of course we could have inferred from

symmetry considerations. Let us now define a non-dimensional temperature, τ , as follows:

τ =

2RT

(7.12)

and call the value of τ at the critical temperature τ

. Substituting this definition in (7.8),

and with X

given by the physical solution of (7.11), we find that τ

is given by:

=4X

(

1 −X

)

[

−

(

1 −K

)(

1 −3X

)

]

. (7.13)

This is a remarkable result: given that X

depends only on K

, the non-dimensional critical

temperature, τ

, is also a function of K

only. But, alas, this concise and rather elegant

357 7.2 Location of the critical mixing point

0 0.2 0.4 0.6 0.8 1

0.5

0.6

0.7

0 0.2 0.4 0.6 0.8 1

0.9

0.95

supercritical mixing

(one phase)

subcritical mixing

(two phases)

Fig. 7.3

Calculated composition (X

) and non-dimensional temperature (τ

) at the critical mixing point, for (possibly

hypothetical) solutions with temperature-independent excess Gibbs free energy of mixing.

result is true only because we assumed that G

excess

is not a function of temperature, and is

given by the simple Margules function. Since the Margules approximation is no more than

an empirical fit, with little physical fundamentation, we should not expect equation (7.13)

to provide more than a rough approximation to the behavior of real solutions.

Even if equations (7.11) and (7.13) are no more than simplified models for the behavior

of real solutions, the results, which are summarized in Fig. 7.3, help make the significance

of the critical mixing temperature clear. The figure shows X

and τ

as functions of K

Note that K

is defined to be ≤ 1, and although it could in principle also be negative,

such behavior (which corresponds to Fig. 5.13d) is uncommon and is not included in the

figure. The figure shows that, starting from the value X

= 0.5 for a symmetric solution,

increasing asymmetry causes the composition of the critical mixture to shift in the direction

of the component that is associated with the larger interaction parameter (X

> 0.5), i.e.

the component that is responsible for generating the greatest amount of excess Gibbs free

energy of mixing. We will see in the next section that this asymmetry carries over into

the subcritical region. Symmetric solutions also have the largest value of non-dimensional

critical temperature, τ

= 1. Note that τ

decreases to a minimum of ∼0.89 for K

∼0.5,

but this range may have little practical significance in planetary processes. Figure 7.3

illustrates how equations (7.11) and (7.13) encapsulate a fundamental property of critical

mixing. Namely, all non ideal solutions (W

= 0) are in principle capable of exhibiting

critical mixing behavior. This means that all non-ideal solutions can undergo a continuous

phase transition between a supercritical one-phase region at τ>τ

, and a subcritical region

at τ<τ

that, in a binary system, is populated by two phases (Fig. 7.3, right panel). For

a given value of K

(asymmetry) the absolute value of the critical temperature is a linear

function of the interaction parameter W

, given by (7.12). This leads naturally to a couple

of important considerations, that arise from the fact that the stabilities of phases, both

supercritical and subcritical, unavoidably terminate at some discontinuous phase boundary.

If the excess Gibbs free energy of mixing is small then the critical mixing point may occur

at a temperature lower than that at which the supercritical phase breaks down to a lower-

entropy assemblage, i.e. the critical mixing point is metastable. The critical temperature may

also be sufficiently low that subcritical unmixing, even if thermodynamically favored, is